Trigonometry/Print version
| This is the print version of Trigonometry You won't see this message or any elements not part of the book's content when you print or preview this page. |
Note: current version of this book can be found at http://en.wikibooks.org/wiki/Trigonometry
Remember to click "refresh" to view this version.
Contents
editAlgebra
- Geometry
- Trigonometry
- Introduction (page 1)
- In simple terms
- Radian and Degree Measure
- The Unit Circle
- Trigonometric Angular Functions
- Right Angle Trigonometry
- Graphs of Sine and Cosine Functions
- Graphs of Other Trigonometric Functions
- Inverse Trigonometric Functions
- Applications and Models
- Analytic Trigonometry
- Using Fundamental Identities
- Verifying Trigonometric Identities
- Solving Trigonometric Equations
- Sum and Difference Formulas
- Multiple-Angle and Product-to-sum Formulas
- Additional Topics in Trigonometry
- Law of Sines
- Law of Cosines
- Vectors in the Plane
- Vectors and Dot Products
- Trigonometric Form of the Complex Number
- Trigonometric Unit Circle and Graph Reference
- Trigonometric Formula Reference
- Trigonometric Identities Reference
- Natural Trigonometric Functions of Primary Angles
Prerequisites And Basics
editTo be able to study Trigonometry successfully, it is recommended that students complete Geometry and Algebra prior to digging in to the course material. Students should also be familiar with the arithmetic of the real number system. It is helpful to have a graphing calculator and graph paper on hand to be able to follow along as well. If one is not available, software available on sites such as GraphCalc or GeoGebra may be helpful. Geometric constructions proposed in the text can be drawn using Geops, free software for performing geometric constructions in the manner of the Ancient Greeks.
Next Page: In simple terms
Home: Trigonometry
Introduction
editTrigonometry is the study of the properties of triangles.
- "Tri" is Ancient Greek word for three,
- "gon" means angle,
- "metry" measurement
Together they make "measuring three angles of a triangle".
If you know some facts about a triangle, such as the lengths of its sides, then using trigonometry you can find out other facts about it. If you know the lengths of sides then you can find what the angles are. If you know the length of one side and of two of the angles, then you can work out what the remaining angle is, and also what the lengths of the other two sides are.
As a consequence the Ancient Greeks were able to use trigonometry to calculate the distance from the Earth to the Moon.
Starting to Learn Trigonometry
edit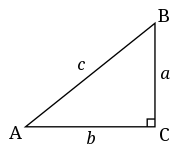
One of the first things we learn in trigonometry is how to calculate what the third angle in a triangle is when given the other two angles. For example, in a triangle if two of the angles are then the third angle must be too, since we know that they all need to add up to .
However, if we're instead told two lengths, say 7cm and 10cm, and if we're not told anything about the angles, then the third length has a range of possibilities, it could be anywhere between 0 and 17cm.
Solving in a Right Triangle
editRemember, a right triangle has one angle that measures (a "right angle"). It's much simpler to calculate the missing third angle on a right triangle, so we will start by examining one, expect to see many more of them in the rest of this book.
In a right triangle we can work out the length of the longest side if given the lengths of the two shorter sides. In a right triangle the lengths of the sides have a particularly nice relationship to each other. The formula for this relationship is written:
The sides and are the ones that touch the angle and is the longer diagonal side that is across from it. You may sometimes see called the hypotenuse.
See Pythagoras' Theorem to start using this formula to calculate the length of that missing side.
Solving in Other Shapes
editWhat if the triangle isn't a right-angled triangle, though?
More complex triangles can easily be divided into right triangles, so we learn about right-angled triangles enables us to work with other kinds of triangles too. Trigonometry and trigonometric functions can also be used with more complex shapes such as squares, hexagons, circles and ellipses. Ultimately the most important mathematical tools we have for measuring the universe are based on the study of the mathematics of triangles.
Trigonometry is a fundamental step in your mathematical education. From the seemingly simple shape, the right triangle, we gain tools and insight that help us in practical and theoretical endeavors. The subtle mathematical relationships between the right triangle, the circle, the sine wave, and the exponential curve can only be fully understood with a firm foundation in trigonometry.
Applications

Because many physical questions can be framed in terms of triangles, trigonometry has found wide use in the physical sciences and engineering.
Trigonometry is needed in surveying and architecture since relationships between lengths and angles in triangles are used directly.
Civil engineers, mechanical engineers, and physicists use trigonometry to understand how forces will be applied, and what direction different objects will move in when they push on or bump into each other.

Since trigonometric functions map to circles, and circles map to waves (we'll get to how all this works!), electrical engineers use trigonometry to make calculations about wavy patterns that they work with, such as AC power that comes out of your wall, or radio signals to your cell phone.
Computer graphics in movies and video games are actually millions of small triangles rendered on your screen, although there are a lot of little tricks that happen after that to make things look smooth and curvy.
In simple terms
editThis page started life as an introduction to the most basic concepts of trigonometry, such as measuring an angle. Done properly this is an advanced topic. This page has now been moved/renamed into book 3 to take on that role, and needs considerable revision. Some content that is still here may need to be integrated back into book 1 |
Introduction to Angles
edit
An angle is formed when two lines intersect; the point of intersection is called the vertex. We can think of an angle as the wedge-shaped space between the lines where they meet. Note that if both lines are extended through the meeting point, there are in fact four angles.
The size of the angle is the degree of rotation between the lines. The more we must rotate one line to meet the other, the larger the angle is.
Suppose you wish to measure the angle between two lines exactly so that you can tell a remote friend about it: draw a circle with its center located at the meeting of the two lines, making sure that the circle is small enough to cross both lines, but large enough for you to measure the distance along the circle's edge, the circumference, between the two cross points. Obviously this distance depends on the size of the circle, but as long as you tell your friend both the radius of the circle used, and the length along the circumference, then your friend will be able to reconstruct the angle exactly.
Definition of an Angle
editAn angle is determined by rotating a ray about its endpoint. The starting position of the ray is called the initial side of the angle. The ending position of the ray is called the terminal side. The endpoint of the ray is called its vertex. Positive angles are generated by counter-clockwise rotation. Negative angles are generated by clockwise rotation.
Consequently an angle has four parts: its vertex, its initial side, its terminal side, and its rotation.
An angle is said to be in standard position when it is drawn in a cartesian coordinate system in such a way that its vertex is at the origin and its initial side is the positive x-axis.

Definition of a Triangle
editA triangle is a planar (flat) shape with three straight sides. An angle is formed between each two sides of a triangle, and a triangle has three angles, hence the name tri-angle. So a triangle has three straight sides and three angles.
If you give me three lengths, I can only make a triangle from them if the greatest length is less than the sum of the other two. Three lengths that do not make the sides of a triangle are your height, the height of the nearest tree, the distance from the top of the tree to the center of the sun.
Triangle Ratios
editAngles are not affected by the length of lines: an angle is invariant under transformations of scale, that is:
If you make the triangle bigger,
but keep the sides in the same ratio,
its angles won't change.
Right Angles
editAn angle of particular significance is the right angle: the angle at each corner of a square or a rectangle. A rectangle can always be divided into two triangles by drawing a line from one corner of the rectangle to the opposite corner.
It is also true that every right-angled triangle is half a rectangle.

A rectangle has four sides; they are generally of two different lengths: two long sides and two short sides. (A rectangle with all sides equal is a square.) When we split the rectangle into two right-angled triangles, each triangle has a long side and a short side from the rectangle as well as a copy of the split line.
So the area of a right-angled triangle is half the area of the rectangle from which it was split. Looking at a right-angled triangle, we can tell what the long and short sides of that rectangle were; they are the sides, the lines, that meet at a right angle. The area of the complete rectangle is the long side times the short side. The area of a right-angled triangle is therefore half as much.
Right Triangles and Measurement
edit
It is possible to bisect any angle using only circles (which can be drawn with a compass) and straight lines by the following procedure:
- Call the vertex of the angle O. Draw a circle centered at O.
- Mark where the circle intersects each ray. Call these points A and B.
- Draw circles centered at A and B with equal radii, but make sure that these radii are large enough to make the circles intersect at two points. One sure way to do this is to draw line segment AB and make the radius of the circles equal to the length of that line segment. On the diagram, circles A and B are shown as near-half portions of a circle.
- Mark where these circles intersect, and connect these two points with a line. This line bisects the original angle.
A proof that the line bisects the angle is found in Proposition 9 of Book 1 of the Elements.
Given a right angle, we can use this process to split that right angle indefinitely to form any binary fraction (i.e., , e.g. ) of it. Thus, we can measure any angle in terms of right angles. That is, a measurement system in which the size of the right angle is considered to be one.
Introduction to Radian Measure
editUnderstanding the three sides of a Radian
editTo illustrate how the three sides of a radian relate to one another try the below thought experiment:
- Assume you have a piece of string that is exactly the length of the radius of a circle.
- Assume you have drawn a radian in the same circle. The radian has 3 points. One is the center of your circle and the other two are on the circumference of the circle where the sides of the radian intersect with the circle.
- Attach one end of the string at one of the points where the radian intersects with the circumference of the circle.
- Take the other end of the string and, starting at the point you chose in Step 2 above, trace the circumference of the circle towards the second point where the radian intersects with the circle until the string is pulled tight.
- You will see that the end of the string travels past the second point.
- This is because the string is now in a straight line. However, the radian has an arc for its third side, not a straight line. Even though a radian has three equal sides, the arc's curve causes the two points where the radian intersects with the circle to be closer together than they are to the third point of the triangle, which is at the center of our circle in this example.
- Now, with the string still pulled tight, find the half way point of the string, then pull it onto the circumference of the circle while allowing the end of the string to move along the circle's circumference. The end of the string is now closer to the second point because the path of the string is closer to the path of the circle's circumference.
- We can keep improving the fit of the string's path to the path of the circle's circumference by dividing each new section of the string in half and pulling it towards the circumference of the circle.
Is a radian affected by the size of its circle?
editDoes it matter what size circle is used to measure in radians? Perhaps using the radius of a large circle will produce a different angle than that produced by the radius of a small circle. The answer is no.

Recall our radian and circle from the experiment in the subsection above. Draw another circle inside the first circle, with the same center, but with half the radius. You will see that you have created a new radian inside the smaller circle that shares the same angle as the radian in the larger circle. We know that the two sides of the radians emanating from the center of the circles are equal to the radius of their respective circle. We also know that the third side of the radian in the larger circle (the arc) is also equal to the larger circle's radius. But how do we know that the third side of the radian in the smaller circle (the arc that follows the circumference of the smaller circle) is equal to the radius of the smaller circle? To see why we do know that the third side of the smaller circle's radian is equal to its radius, we first connect the two points of each radian that intersect with the circle with each other. By doing so, you will have created two isosceles triangles (triangles with two equal sides and two equal angles).
An isosceles triangle has two equal angles and two equal sides. If you know one angle of any isosceles triangle and the length of two sides that make up that angle, then you can easily deduce the remaining characteristics of the isosceles triangle. For instance, if the two equidistant sides of an isosceles triangle intersect to form an angle that is equal to 40o, then you know the remaining angles must both equal 70º. Since we know that the equidistant sides of our two isosceles triangles make up our known angle, then we can deduce that both of our radians (when converted to isosceles triangles with straight lines) have identical second and third angles. We also know that triangles with identical angles, regardless of their size, will have the length of their sides in a constant ratio to each other. For instance, we can deduce that an isosceles triangle will have sides that measure 2 meters by 4 meters by 4 meters if we know that an isoscleses triangle with identical angles measures 1 meter by 2 meters by 2 meters. Therefore, in our example, our isosceles triangle formed by the second smaller circle will have a third side exaclty equal to half of the third side of the isosceles triangle created by the larger circle. The relationship between the size of the sides of two triangles that share identical angles is also found in the relationship between radius and circumference of two circles that share the same center point - they will share the exact same ratio. In our example then, since the radius of our second smaller circle is exactly half of the larger circle, the circumference between the two points where the radian of the smaller circle intersect (which we have shown is one half of the distance between the two similar points on the larger circle) will share the same exact ratio. And there you have it - the size of the circle does not matter.
Using Radians to Measure Angles
editOnce we have an angle of one radian, we can chop it up into binary fractions as we did with the right angle to get a vast range of known angles with which to measure unknown angles. A protractor is a device which uses this technique to measure angles approximately. To measure an angle with a protractor: place the marked center of the protractor on the corner of the angle to be measured, align the right hand zero radian line with one line of the angle, and read off where the other line of the angle crosses the edge of the protractor. A protractor is often transparent with angle lines drawn on it to help you measure angles made with short lines: this is allowed because angles do not depend on the length of the lines from which they are made.
If we agree to measure angles in radians, it would be useful to know the size of some easily defined angles. We could of course simply draw the angles and then measure them very accurately, though still approximately, with a protractor: however, we would then be doing physics, not mathematics.
The ratio of the length of the circumference of a circle to its radius is defined as 2π, where π is an invariant independent of the size of the circle by the argument above. Hence if we were to move 2π radii around the circumference of a circle from a given point on the circumference of that circle, we would arrive back at the starting point. We have to conclude that the size of the angle made by one circuit around the circumference of a circle is 2π radians. Likewise a half circuit around a circle would be π radians. Imagine folding a circle in half along an axis of symmetry: the resulting crease will be a diameter, a straight line through the center of the circle. Hence a straight line has an angle of size π radians.
Folding a half circle in half again produces a quarter circle which must therefore have an angle of size π/2 radians. Is a quarter circle a right angle? To see that it is: draw a square whose corner points lie on the circumference of a circle. Draw the diagonal lines that connect opposing corners of the square, by symmetry they will pass through the center of the circle, to produce 4 similar triangles. Each such triangle is isoceles, and has an angle of size 2π/4 = π/2 radians where the two equal length sides meet at the center of the circle. Thus the other two angles of the triangles must be equal and sum to π/2 radians, that is each angle must be of size π/4 radians. We know that such a triangle is right angled, we must conclude that an angle of size π/2 radians is indeed a right angle.
Summary and Extra Notes
editIn summary: it is possible to make deductions about the sizes of angles in certain special conditions using geometrical arguments. However, in general, geometry alone is not powerful enough to determine the size of unknown angles for any arbitrary triangle. To solve such problems we will need the help of trigonometric functions.
In principle, all angles and trigonometric functions are defined on the unit circle. The term unit in mathematics applies to a single measure of any length. We will later apply the principles gleaned from unit measures to larger (or smaller) scaled problems. All the functions we need can be derived from a triangle inscribed in the unit circle: it happens to be a right-angled triangle.
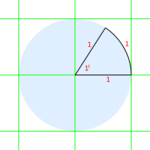
The center point of the unit circle will be set on a Cartesian plane, with the circle's centre at the origin of the plane — the point (0,0). Thus our circle will be divided into four sections, or quadrants.
Quadrants are always counted counter-clockwise, as is the default rotation of angular velocity (omega). Now we inscribe a triangle in the first quadrant (that is, where the x- and y-axes are assigned positive values) and let one leg of the angle be on the x-axis and the other be parallel to the y-axis. (Just look at the illustration for clarification). Now we let the hypotenuse (which is always 1, the radius of our unit circle) rotate counter-clockwise. You will notice that a new triangle is formed as we move into a new quadrant, not only because the sum of a triangle's angles cannot be beyond 180°, but also because there is no way on a two-dimensional plane to imagine otherwise.
Radian and Degree Measure
editThere are in
a complete circle
Units of Measure
editWe have been measuring angles in degrees, with in a complete circle. However, what if we measured the circle according to how many units we went around it. Think about it this way, do you measure the runner going around the circular track according to the degrees from the centre or the meters around the circle? The obvious answer is meters around the circle. However, how do you measure this in trigonometry?
Choice of Units for Length and Weight
editIn measuring many quantities we have a choice of units. For example with distances we can use the metric system and measure in metres, kilometres, centimetres, millimetres. It is also possible to measure distances in miles, yards, feet and inches. With weights we can measure in kilogrammes and grammes. We can also measure in pounds and ounces.
Choice of Units for Measuring Time
editIn measuring time we choose to have 60 seconds in a minute and 60 minutes in an hour. We could devise a new more metric system for time and divide an hour into 100 units, each three fifths of our current minute, and then divide these shorter 'minutes' up into 100 units each of which would be about a third of a second.
Why 60? Why 360?
editThe choice of dividing into 60 is not entirely arbitrary. 60 can be divided evenly into 2,3,4,5 or 6 or 10 or 12 parts. 60 can't be divided evenly into 7 equal parts, each a whole number in size, but it's still pretty good. Using 360 degrees in a full circle gives us many ways to divide the circle evenly with a whole number of degrees. Nevertheless, we could divide the circle into other numbers of units.
Metric Degrees?
editFrom the earlier talk of the metric system you might be anticipating that we are about to divide the circle up into 100 or 1000 'degrees'. There is actually a unit called the 'grade' or 'Gradian' (Grad on calculators which have it) in which angles are measured by dividing a right angle up into 100 equal parts, each of one Gradian in size. One Gradian is 0.9 of a degree - quite close to being one degree. The grade is in turn divided into 100 minutes and one minute into 100 seconds. This centesimal system (from the Latin centum, 100) was introduced as part of the metric system after the French Revolution. The Gradian unit is nothing like as widely used as either degrees or the units that interests us most on this page. The unit we introduce here is called the Radian.
Radians is the circumference measure at
the point from .
Choice of Units for Radians
editRadians are quite large compared to degrees (and to Gradians). There are about 6.28 Radians to a complete circle. There are about 57.3 degrees in one Radian.
|
Exercise: Check the Statements Are the statements:
Compatible? It is not hard to check.
|
We said "there are about 6.28 Radians to a complete circle". The exact number is , making the number of radians in a complete circle the same as the length of the circumference of a unit circle.
Remember that:
The circumference of a circle is
where is the radius.
Justifying Choice of Units for Radians
editAt this stage in explaining trigonometry it is rather difficult to justify the use of these strange units. There aren't even an exact whole number of radians in a complete circle. In more advanced work, particularly when we use calculus they become the most natural units to use for angles with functions like and . A flavour of that, but it is only a hint as to why it is a good unit to use, is that for very small angles.
And the approximation is better the smaller the angle is. This only works if we choose Radians as our unit of measure and very small angles.
|
Worked Example: Small angles in Radians and Degrees We claim that for small angles measured in radians the angle measure and the sine of the angle are very similar.
Let us take one millionth of a circle. In degrees that is 0.00036 degrees. In Radians that is Radians. The angle of course is the same. It's one millionth of a circle, however we choose to measure it. It is just as with weights where a weight is the same whether we measure it in kilogrammes or pounds. The sine of this angle, which is the same value whether we chose to measure the angle in degrees or in radians, it turns out, is about 0.00000628. If your calculator is set to use degrees then will give you this answer. |
The Radian Measure
editThere are
Radians
in a complete circle.
It is traditional to measure angles in degrees; there are 360 degrees in a full revolution. In mathematically more advanced work we use a different unit, the radian. This makes no fundamental difference, any more than the laws of physics change if you measure lengths in metres rather than inches. In advanced work, If no unit is given on an angle measure, the angle is assumed to be in radians.
A notation used to make it really clear that an angle is being measured in radians is to write 'radians' or just 'rad' after the angle. Very very occasionally you might see a superscript c written above the angle in question.
What You need to Know
editFor book one of trigonometry you need to know how to convert from degrees to radians and from radians to degrees. You also need to become familiar with frequently seen angles which you know in terms of degrees, such as in terms of radians as well (it's Radians). Angles in Radians are nearly always written in terms of multiples of Pi.
You will also need to be familiar with switching your calculator between degrees and radians mode.
Everything that is said about angles in degrees, such as that the angles in a triangle add up to 180 degrees has an equivalent in Radians. The angles in a triangle add up to Radians.
Defining a radian
editA single radian is defined as the angle formed in the minor sector of a circle, where the minor arc length is the same as the radius of the circle.

Measuring an angle in radians
editThe size of an angle, in radians, is the length of the circle arc s divided by the circle radius r.

We know the circumference of a circle to be equal to , and it follows that a central angle of one full counterclockwise revolution gives an arc length (or circumference) of . Thus radians corresponds to , that is, there are radians in a circle.
Converting between Radians and Degrees
editBecause there are radians in a circle:
To convert degrees to radians:
To convert radians to degrees:
Exercises
edit|
Conversion from degrees to radians
|
|
Conversion from radians to degrees
|
The Unit Circle
editThe Unit Circle is a circle with its center at the origin (0,0) and a radius of one unit.

Angles are always measured from the positive x-axis (also called the "right horizon"). Angles measured counterclockwise have positive values; angles measured clockwise have negative values.
Defining sine and cosine in terms of the unit circle
editIn the unit circle shown here, a unit-length radius has been drawn from the origin to a point (x, y) on the circle.

A line perpendicular to the x-axis, drawn through the point (x, y), intersects the x-axis at the point with the abscissa x. Similarly, a line perpendicular to the y-axis intersects the y-axis at the point with the ordinate y. The angle between the x-axis and the radius is .
So, we can say that the sine of an angle is the ordinate of the point on the unit circle at that angle, and the cosine of an angle is the abscissa of the point on the unit circle at that angle.
We define the basic trigonometric functions of any angle as follows:
can be algebraically defined.
These three trigonometric functions can be used whether the angle is measured in degrees or radians as long as it specified which, when calculating trigonometric functions from angles or vice versa.
Alternative definitions
edit- A previous chapter used Soh-Cah-Toa to define the trigonometric functions. The advantage of the unit circle is that θ can be extended outside the first quadrant , which allows us to define these functions on the interval .
- If trigonometry is applied to vectors, it is more convenient, if the radius of the circle is not equal to unity. For example, if vector A has magnitude :
It is important to know why the above equations are true. Knowing , . The same could be said for the definition for . Finally, the final line is the Pythagorean identity.
Video links
editMore about this topic can be found at the 'Khan Academy:'
Some values for sine and cosine
editA unit circle with certain exact values marked on it is below:

Unit circles form the basis of most analog clocks and animations on computers since the cos and sin correspond to the x and y positions of the end of the line segments representing the hands of the clock.
The unit circle on the left has the degree, the radian, and the coordinate value on the unit circle. For a coordinate value , if walking around the circle radians anti-clockwise from the horizontal axis, the coordinate value at which the person walked around the circle is .
Remember that on a unit circle, the angle anti-clockwise from the horizontal axis gives and . The same is true for radians. As such, for corresponding to on the unit circle, radians when substituted in the cosine or sine function is the coordinate value on the unit circle. That is:
- , OR, equivalently,
The unit circle is very useful to your mathematical studies of trigonometry because it tells you the EXACT value of certain angles. Later, you will learn how to find other ratios of angles and radians without needing to rely on the special values of the unit circle – 30, 45, 60, and 90.
It is worth your time memorizing some of the values of sine and cosine on the unit circle (cosine is equal to while sine is equal to ). You should at least become familiar with the values for and know where are on the unit circle.
If you have some trouble memorizing the values, here are some helpful hints and patterns. Try to find some more other than what is listed.
- The coordinate value on the unit circle has the decrease from in the -value coordinate at to at . The denominator is always . Here, see what we mean. Ignore the y-value for now:
- , , .
- Like the -value coordinate, the -value coordinate has a pattern in the numerator. As the angle increases, between and (inclusive), the increases from in the -value coordinate at to at . From the above bullet, putting it together, you get the following pattern:
- , , .
- Certain radian values are simply reflections of the other. Take a look at the ones with the same denominator and see if you can correspond any patterns to what you see.
If you are to ever be tested on this, make a quick sketch of the first quadrant of the circle, and remember the pattern that underlies the unit circle.
|
Clock Hands
|
Trigonometric Angular Functions
editGeometrically defining tangent
editIn the previous section, we algebraically defined tangent as , and this is the definition that we will use most in the future. It can, however, be helpful to understand the tangent function from a geometric perspective.

A line is drawn at a tangent to the unit circle: (i.e. ). Another line is drawn from the point on the radius of the circle where the given angle falls, through the origin(O), to a point (Q) on the drawn tangent. The ordinate (QP) of this point is called the tangent of the angle.
The slope of the line OQ = and as we mentioned before
KC = sin(θ) , OC = cos(θ)
Hence , the Slope of the line OQ =
and also the slope of OQ = = = = tan(θ)
Hence , we can deduce that tan(θ) = = = QP = the ordinate of the point Q = the slope of OQ
Domain and range of circular functions
editAny size angle, positive or negative, can be the input to sine or cosine — the result will be as if the largest multiple of 2π (or 360°) were subtracted from or added to the angle. The output of the two functions is limited by the absolute value of the radius of the unit circle, .
R represents the set of all real numbers.
No such restrictions apply to the tangent, however, as can be seen in the diagram in the preceding section. The only restriction on the domain of tangent is that odd integer multiples of are undefined, as a line parallel to the tangent will never intersect it.
for a deep understanding of trigonometric functions explore this Applet
Applying the trigonometric functions to a right-angled triangle
editIf you redefine the variables as follows to correspond to the sides of a right triangle:
• x = a (adjacent)
• y = o (opposite)
• a = h (hypotenuse)
Next Page: Right Angle Trigonometry
Previous Page: The unit circle
Home: Trigonometry
Right Angle Trigonometry
edit| This page is in need of attention. You can help improve it, request project assistance, or view current progress. |
Construction of Right Triangles
edit
Right triangles are easily constructed. Recall that a diameter is a straight line which starts at one point on the circle and goes through the center to the other side. Using this property of a circle:
- Construct a diameter of a circle. Call the points where the diameter touches the circle a and c.
- Choose a distinct point b on the circle (any point that is neither a nor c).
- Construct line segments connecting points a, b and c.
Provided the above three directions are followed, the resulting triangle Δabc will be a right triangle. This result is known as Thales' theorem.
This right triangle can be further divided into two isosceles triangles by adding a line segment from b to the center of the circle.
To simplify the following discussion, we specify that the circle has diameter 1 and is oriented such that the diameter drawn above runs left to right. We shall denote the angle of the triangle at the right θ and that at the left φ. The sides of the right triangle will be labeled, starting on the right, a, b, c, so that a is the rightmost side, c the leftmost, and b the diameter. We know from earlier that side b is opposite the right angle and is called the hypotenuse. Side a is opposite angle φ, while side c is opposite angle θ. We reiterate that the diameter, now called b, shall be assumed to have length 1 except where otherwise noted.
By constructing a right angle to the diameter at one of the points where it crosses the circle and then using the method outlined earlier for producing binary fractions of the right angle, we can construct one of the angles, say θ, as an angle of known measure between 0 and π / 2. The measure of the other angle φ is then π - π/2 - θ = π/2 - θ, the complement of angle θ. Likewise, we can bisect the diameter of the circle to produce lengths which are binary fractions of the length of the diameter. Using a compass, a binary fractional length of the diameter can be used to construct side a (or c) having a known size (with regard to the diameter b) from which side c can be constructed.
Using Right Triangles to find Unknown Sides
editFinding unknown sides from two other sides
editFrom the Pythagorean Theorem, we know that:
Recall that c (the diameter/hypotenuse in the above example) has been defined as having a length of one, therefore:
permits us to calculate the length of b squared. It may happen that b squared is a fraction such as 1/4 for which a rational square root can be found, in this case as 1/2, alternatively, we could use Newton's Method to find an approximate value for b.
Finding unknown sides from one side and one (non-right) angle
editAs any triangle could be compared to our basic triangle (formed from a circle with a diameter of one), a table enumerating the relationships between angles and side lengths would be very useful to understanding the properties of any triangle. However, such a table would be unwieldy in practice and it is often not necessary to know the exact value.
Of course, given an angle , we could construct a right angled triangle using ruler and compass that had as one of its angles, we could then measure the length of the side that corresponds to a to evaluate the function. Such measurements would necessarily be inexact; it would be a problem in physics to see how accurately such measurements can be made; using trigonometry we can make precise predictions with which the results of these physical measurements can be compared.
The most common way of communicating the idea that relationships exist without providing exact details takes the form of a 'function'. A function is like a machine that takes some simple input and produces some simple output. Usually a function defines some kind of rule ([Function]) and provides us a handy notation useful in trigonometry. That way, we know that we're using a certain relationship without needing to know the exact numerical values. Basic trigonometric functions are simply stand-ins for the relationship between angles and sides of a triangle.
One such function, which allows us to know the relationship between any value of and the corresponding value of is called the cosine or . This universal relationship is represented as: which would save us the work of constructing angles and lengths and making difficult deductions from them.
This means that if you know the cosine of an angle, you also know the relationship between the lengths of the sides. The actual size of the triangle can be bigger or smaller, but the mathematical relationship represented by the cosine does not change so long as the size of the angle remains constant.
Cosine example
editSome explicit values for the cos function are known. For , sides and coincide: , so . For , sides and coincide and are of length 1, and side is of zero length, consequently , . and .
The simplest right angle triangle we can draw is the isosceles right angled triangle, it has a pair of angles of size radians, and if its hypotenuse is considered to be of length one, then the sides and are of length as can be verified by the theorem of Pythagoras. If the side is chosen to be the same length as the radius of the circle containing the right angled triangle, then the right hand isosceles triangle obtained by splitting the right angled triangle from the circumference of the circle to its center is an equilateral triangle, so must be , and must be and must be .
Properties of the cosine and sine functions
editPeriod
editA full revolution is an angle of 2π radians, so increasing an angle by this amount gets you exactly back to your starting point. Therefore, a perfect circle is maintained, along with the relationships formed by triangles within, by adding 2π to any angle θ. This is called the period, --the size of the angle or the time period over which the relationships begin to repeat (correlating the two is complex, and allows us to talk about wave theory).
Using functions, we can represent this fact in terms of the cosine function by stating that :
Knowing the period of the sine and cosine functions (and by derivation, that of other functions) is useful because it means that we can substitute one angle for another when we know that the period is the same. This helps in calculations, such as when there is the need to add or subtract angles.
Half Angle and Double Angle Formulas
editWe can derive a formula for cos(θ/2) in terms of cos(θ) which allows us to find the value of the cos() function for many more angles. To derive the formula, draw an isosceles triangle, draw a circle through its corners, connect the center of the circle with radii to each corner of the isoceles triangle, extend the radius through the apex of the isoceles triangle into a diameter of the circle and connect the point where the diameter crosses the other side of the circle with lines to the other corners of the isoceles triangle.
Therefore:
which gives a method of calculating the cos() of half an angle in terms of the cos() of the original angle. For this reason * is called the "Cosine Half Angle Formula".
The half angle formula can be applied to split the newly discovered angle which in turn can be split again ad infinitum. Of course, each new split involves finding the square root of a term with a square root, so this cannot be recommended as an effective procedure for computing values of the cos() function.
Equation * can be inverted to find cos(θ) in terms of cos(θ)/2:
substituting gives:
that is a formula for the cos() of double an angle in terms of the cos() of the original angle, and is called the "cosine double angle sum formula".
Next Page: Trigonometric identities
Previous Page: Trigonometric Angular Functions
Home: Trigonometry
Graphs of Sine and Cosine Functions
editThe graph of the sine function looks like this:
Careful analysis of this graph will show that the graph corresponds to the unit circle. x is essentially the degree measure (in radians), while y is the value of the sine function.
The graph of the cosine function looks like this:
As with the sine function, analysis of the cosine function will show that the graph corresponds to the unit circle. One of the most important differences between the sine and cosine functions is that sine is an odd function (i.e. while cosine is an even function (i.e. .
Sine and cosine are periodic functions; that is, the above is repeated for preceding and following intervals with length .
Exercises
edit|
When does Sine = Cosine? For what value of does ? (Choose a value between 0° and 90° or equivalently in radians between 0 and ).
|
Graphs of Other Trigonometric Functions
editA graph of . is defined as .
A graph of . is defined as .
A graph of . is defined as .
A graph of . is defined as or .
Note that , , and are unbounded, positive or negative. While (and ) can take any value, and can never lie between -1 and 1.
Inverse Trigonometric Functions
editThe Basic Idea
editIn the equation
if we are given we can work out .
If we are given , can we work out ?
Look at the graph of and you will see that for or there aren't any answers at all, whilst for other values of there are infinitely many answers.
If
we write the inverse of as follows
Notice the strange notation. It's just a convention, and does not really fit in well with the convention of meaning . However, we are stuck with this notation. It is so widely used and so familiar in mathematical work that in practice it does not cause confusion. On many calculators the alternative notation is used.
A calculator will only give one answer (or error) for . You can get some of the other answers by adding or subtracting multiples of 360°. In a later section we spell out the conventions as to which answer is given by .
arcsin
editA common notation used for the inverse functions is the "arcfunction" notation, prefixing the function name by "arc" or sometimes just "a".
- ,
- , and
- .
The arcfunctions might perhaps be so named because of the relationship between radian measure of angles and arclength--the arcfunctions yield arc lengths on a unit circle.
The Inverse Functions, Domain and Range
editThe inverse of sine or cosine for some values has multiple answers and some values does not exist at all. We'd like it if the inverse were a function, but according to the mathematical definition of a function it is not:
- A function is something that given one value always gives back a unique value as its 'answer'.
is a function because given any x it gives back some value. There is not really a function that is an inverse for because, for example, and have the same value. The inverse 'function' does not know whether to go back to 20° or 160°.
To deal with this we need some more mathematical language. We have mathematical terminology for what a function operates on and where its values end up. A function like needs to be accompanied by some agreement as to what values it can operate on and where they end up. By convention , though is also a valid solution to . So how do we describe this kind of thing?
- The domain of a function is the set of values which it is defined on.
|
Example: Reciprocal function The function is defined on all values of x except for 0. Its domain is the real numbers excluding zero. |
|
Example: Factorial function The factorial function, operates on the positive whole numbers. As a function f - . The factorial function is usually written by writing an exclamation point after a number. So, 3 factorial is usually written as 3! and it is . 4 factorial is written as 4! and it is . The domain of the factorial function is the positive whole numbers. |
- The range of a function is the set of values which it can take. The range will depend on the domain too.
|
Range of x2 Consider the function If we use ordinary numbers for x like 37.2 or -1001.56 we always find is a positive number (or zero). The range of is the numbers greater than or equal to zero. |
|
Range of 2x Consider the function If we choose the domain of to be the numbers greater than or equal to 1, then the range of is the numbers greater than or equal to two. |
More Notation
edit- The integers are whole numbers like 1,2,3,4 and also include 0, -1, -2,-3... A symbol we use to indicate the integers is . The statement means exactly the same thing as x is an integer.
- The reals include all the integers, and also fractions, and also other numbers like pi, and square root of 2. The reals 'fill in the gaps' between the integers. You'll get a better definition of the reals in a later book. A symbol we use to indicate the reals is . The statement means exactly the same thing as x is a real number.
- A range of numbers in the reals can often be written using interval notation. Here is an example for numbers greater than or equal to zero and less than one: [0,1). The square and round brackets have special meaning. The square bracket means the number is included. A round bracket means the number is excluded.
|
Interval Notation
|
- Function composition is applying one function after another. If we have two functions f and g, we write the composite function, applied to x as: . This means first apply g to x, then apply f to that result. We can regard as a new function in its own right.
- An inverse to a function is written . If is the function that adds 12 to a number, then is the function that subtracts 12 from a number.
Inverses to Trig functions
editSome textbooks 'solve' the problem of inverses for trig functions by defining new functions , , and (all with initial capitals) to equal the original functions but with restricted domain.
With suitably restricted domain the functions , , and (all with initial capitals) do have inverses which are functions too.
The restrictions to allow the inverses to be functions are standard. Here (and for the rest of this page) we are using radians to measure angles rather than degrees:
- has domain
- has domain ; and
- has domain
For each function, the restricted domain includes first-quadrant angles as well as an adjacent quadrant.
Inverses, Really?
editIt is important to note that because of these restricted domains, the inverse trigonometric functions do not necessarily behave as one might expect an inverse function to behave. While
- (following the expected ),
- .
For the inverse trigonometric functions, only when is in the range of the inverse function.
The other direction, however: for all to which we can apply the inverse function.
The Inverse Relations
edit'For completeness', here are definitions of the inverse trigonometric relations based on the inverse trigonometric functions. This section is really mostly about using mathematical notation to express how adding multiples of 360o to an angle gives us another solution for the inverse. Because we are working in radians we're adding multiples of two pi. Some more notation being used here:
- Curly braces like so {} mean the 'set of', i.e. the set of whatever is inside them.
- The symbol is read as union. The union of two sets is everything that is in either of them.
- (the sine function has period , but within any given period may have two solutions and )
- (the cosine function has period , but within any given period may have two solutions and cosine is even: )
- (the tangent function has period and is one-to-one within any given period)
Applications and Models
editSimple harmonic motion
edit
Simple harmonic motion (SHM) is the motion of an object which can be modeled by the following function:
or
- where c1 = A sin φ and c2 = A cos φ.
In the above functions, A is the amplitude of the motion, ω is the angular velocity, and φ is the phase.
The velocity of an object in SHM is
The acceleration is
An alternative definition of harmonic motion is motion such that
Springs and Hooke's Law
editAn application of this is the motion of a weight hanging on a spring. The motion of a spring can be modeled approximately by Hooke's law:
- F = -kx
where F is the force the spring exerts, x is the extension in meters of the spring, and k is a constant characterizing the spring's 'stiffness' hence the name 'stiffness constant'.
Calculus-based derivation
editFrom Newton's laws we know that F = ma where m is the mass of the weight, and a is its acceleration. Substituting this into Hooke's Law, we get
- ma = -kx
Dividing through by m:
The calculus definition of acceleration gives us
Thus we have a second-order differential equation. Solving it gives us
- (2)
with an independent variable t for time.
We can change this equation into a simpler form. By letting c1 and c2 be the legs of a right triangle, with angle φ adjacent to c2, we get
and
Substituting into (2), we get
Using a trigonometric identity, we get:
- (3)
Let and . Substituting this into (3) gives
Next Page: Using Fundamental Identities
Previous Page: Inverse Trigonometric Functions
Home: Trigonometry
Analytic Trigonometry
editUsing Fundamental Identities
editRemembering Formulae
editThis page is about how to remember trig formulas - so it is more than just a summary of trig formulae.
You will need to have read most of the rest of the book for this page to be useful to you.
The Blue-Box Formulae
editIn any triangle the angles
always sum to
In a right angled triangle
The square of the hypotenuse
is equal to
the sum of the squares of the other two sides.
Tips on checking and remembering Formulae
editThis page contains some trigonometric identities. It does not contain all trigonometric identities. It couldn't possibly. As well as the trigonometric identities for 'double angles' such as:
there exist trigonometrical identities for treble angles, quadruple angles and so on. We could not list them all. Also the same formula can be presented in different disguises as we'll see below.
It's useful to learn some of the trig identities and to know how to quickly and easily derive one trigonometric identities from another.
Checking Formulae
editIt is also very important to be able to check that the formulae you come up with make sense. We know that . If your formula for does not give the answer 1 when then it is wrong! Don't stop there though. You can work out where you went wrong and save yourself making the same mistake again. How do you do that?
If you worked out the formula for from the formula for you need to check through the steps you took. If the mistake isn't obvious, try putting and . It is very very easy to get a sign wrong, a plus for a minus, when working with equations quickly. It is only through practice that you will become both fast at it and accurate.
Identities Based on the Pythagorean Theorem
editSome of the most fundamental trigonometric identities are those derived from the Pythagorean Theorem. These are defined using a right triangle:

At this stage in the course the Pythagorean Theorem should be second nature to you. If you have not yet learned it, learn it now.
and of course are the legs or the adjacent and opposite edges, and is the hypotenuse, the longest side, the side that does not include the right angle. This formula only works for a right angle triangle. If the angle shown as a right angle in the diagram were obtuse, larger than a right angle, then would be larger than the Pythagorean sum. If the angle shown as a right angle were smaller than a right angle, then would be smaller than .
Pythagorean Theorem in Terms of sine and cosine
editThe Pythagorean Theorem is the same thing as
We know this from the earlier in the book where we introduced and .
- The is the adjacent side when the hypotenuse is one.
- The is the opposite side when the hypotenuse is one.
The identity should be second nature to you too, but you should also be able to derive it from the Pythagorean relation.
We can see it's true from a right triangle that has a hypotenuse that is 'c' rather than one. Dividing the Pythagorean relation through by gives us
And we have already seen from soh-cah-toa that the sine of A is and the cosine of A is .
Identities based on Addition Formula
editWe saw the addition formula earlier.
Letters are Arbitrary
editThe letters in these equations and are arbitrary. We could equally use and . We're pointing this out because we happen to have a diagram on this page that has angles , and in it, and we want to make it clear that that was for Pythagoras and we're not talking about that diagram any more. In these equations you can also always substitute actual values, e.g. replace by and they'd still be true. Or you could replace by or and they'd still be true.
Addition Formula
editThe addition formula for cosine is:
and is worth learning. But don't learn the next one:
'Subtraction' Formula
editLearning the second formula is extra effort that does not really gain you anything. You can get it instantly by replacing by in the first equation. The only things on the right hand side that will change are the terms that had in them. The is unchanged because . The minus sign before the second term changes because .
Checking the 'subtraction' formula
editNow do a quick check. If then is which is one, right? And on the right hand side we have , which is also one. Looks good.
It is much better to remember it this way, because you are doing less rote learning and you're also becoming more fluent with the algebra.
Double Angle Formula
editYou can immediately get to the next formula by putting B equal to A in the addition formula. This is a double angle formula.
Half Angle Formula
editReplace A by in the previous result and you get the half angle formula.
Cos^2A=\2cos^2A-1
Sum of two shifted Cosines
editFor the next formula, you could just plough through the algebra...
Waves in and out of phase
editBefore we do, notice that we are adding two cosine waves, the first shifted left and the second shifted right. We've seen this before when we looked at waves in and out of phase. We're going to get another sinusoidal wave. The expression is fairly symmetric, and actually we can quickly show that the expression gives an even function, that is that the value for is the same as for :
- using we get to:
- and now swapping the two terms:
- which is the original expression.
with practice you'll be able to see those steps and that the expression is an even function immediately.
A sinusoidal wave that is an even function - well it is something based on cosine. We're expecting the formula will simplify to give us something like:
Where will depend on .
Values to Check With
editWhen (try it in the original formula) we expect A to be 2. When we expect A to be 0, as the two cosine waves are out of phase. So now to plough through the algebra:
And to check we try with and get , and we check with and get , as we hoped.
Knowing roughly what we expected made it easier to get the algebraic steps right. We knew where we were going. We knew we weren't going to end up with four separate terms, some would have to cancel or combine in some other way.
Identities based on Sine and Cosine rules
edit- .
This is easy to remember because it is so symmetrical. You do not even need to remember which way up the ratios are as this is also true:
- .
What you do need to remember is how the triangle is labelled for it to be true.
With the cosine law formula:
It is best to think of it as a more general version of Pythagoras' theorem. The a and b have to be on equal footing, so ab as a multiplier is reasonable.
- If you are familiar with 'units' in physics, then use the fact that units must match up. The quantities are measurements of length. It is no good adding to . One might have units Km2 the other units of Km. Adding to the units, e.g: Km2, do match.
In some more detail, it has got to be minus for . That's because for we need to be less than for Pythagoras' theorem.
How can you remember and be sure the 2 is right? Think of an equilateral triangle with each side of length 1. The angle and . We need the 2 to get the right answer 1 + 1 + 2x1x1x0.5 = 1.
Ratio identities
editThis is one definition of tan, and is something you should just learn.
Identities based on symmetry
editThese symmetry identities are best remembered by remembering the graphs for these functions. Have a look at the graphs again if you don't remember them.
are landmarks on the graphs of sine and cosine, and you should know what happens for both those functions at those landmarks. When you have that knowledge the following symmetry identities are easy to write down, because you can see them visually.
Shifting Left
editThe identities above are visualised as shifting the graph left by . It's a half cycle, and both cosine and sine change signs - and hence tan does not change sign, because when it is expressed as a ratio of sine over cosine both the top and bottom change signs.
Reflecting in
editIn the above we are reflecting the graph about the vertical line . Spend enough time looking at this on the graph to see that that is true. It is important to do that to remember this trick for remembering what happens.
Now sine has a maximum at (it has the value one) and it is symmetric about that x value, so . Cosine is zero at . Reflecting cosine in the line reverses the sign.
Co-function identities
editThe above two formulas are most easily seen from the right-triangle definition of cosine and sine. The two acute angles in such a triangle add up to , and we are just giving the ratios of sides lengths in terms of a different angle's trig function.
These two formulae are 'the same' as the previous formulae. We get there in two steps. First subtracted pi from the angle on the right hand side, which inverts the sign, and inverted the sign to compensate. Next invert the sign of the angle on the right hand side. For cosine on the right we are done. For sine on the right we have to invert its sign since inverting the angle's sign changed the sign of the result.
Yes - keeping track of signs is tricky, and always needs care.
Verifying Trigonometric Identities
editTo verify an identity means to prove that the equation is true by showing that both sides equal one another.
There is no set method that can be applied to verifying identities; there are, however, a few different ways to start based on the identity which is to be verified.
Trigonometric identities are used in both course texts and in real life applications to abbreviate trigonometric expressions. It is important to remember that merely verifying an identity or altering an expression is not an end in itself, but rather that identities are used to simplify expressions according to the task at hand. Trigonometric expressions can always be reduced to sines and cosines, which can be more manageable than other functions.
To verify an identity
edit- Always try to reduce the larger side first.
- Sometimes getting all trigonometric functions on one side can help.
- Remember to use and manipulate already existing identities. The Pythagorean identities are usually the most useful in simplifying.
- Remember to factor if needed.
- Whenever there is a squared trigonometric function such as , always use the Pythagorean identities, which deal with squared functions.
- Sometimes doing the reverse of the normal steps helps. For example, adding 1 in unique forms (such as can help simplify expressions by matching denominators and simplifying numerators.
Easy example
- , so
is the same as
and therefore the example can be rewritten as
Identity verified
Solving Trigonometric Equations
editTrigonometric equations are equations including trigonometric functions. If they have only such functions and constants, then the solution involves finding an unknown which is an argument to a trigonometric function.
Basic trigonometric equations
editsin(x) = n
editThe equation has solutions only when is within the interval . If is within this interval, then we first find an such that:
The solutions are then:
Where is an integer.
In the cases when equals 1, 0 or -1 these solutions have simpler forms which are summarized in the table on the right.
For example, to solve:
First find :
Then substitute in the formulae above:
Solving these linear equations for gives the final answer:
Where is an integer.
cos(x) = n
editLike the sine equation, an equation of the form only has solutions when n is in the interval . To solve such an equation we first find one angle such that:
Then the solutions for are:
Where is an integer.
Simpler cases with equal to 1, 0 or -1 are summarized in the table on the right.
tan(x) = n
editAn equation of the form has solutions for any real . To find them we must first find an angle such that:
After finding , the solutions for are:
When equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
cot(x) = n
editThe equation has solutions for any real . To find them we must first find an angle such that:
After finding , the solutions for are:
When equals 1, 0 or -1 the solutions have simpler forms which are shown in the table on the right.
csc(x) = n and sec(x) = n
editThe trigonometric equations and can be solved by transforming them to other basic equations:
Further examples
editGenerally, to solve trigonometric equations we must first transform them to a basic trigonometric equation using the trigonometric identities. This sections lists some common examples.
a sin(x)+b cos(x) = c
editTo solve this equation we will use the identity:
The equation becomes:
This equation is of the form and can be solved with the formulae given above.
For example we will solve:
In this case we have:
Apply the identity:
So using the formulae for the solutions to the equation are:
Where is an integer.
Sum and Difference Formulas
editSine Formulas
editThe addition formula for sines is as follows:
This is an important tool that allows us to relate the sines and cosines of angles of different sizes.
There is a related formula for cosines, discussed in the next section:
|
Worked Example: Sine of
Answer: Using the first formula: |
|
Exercise: Check the worked example
|
|
Exercise: Sines and Cosines of
|
The addition formulas are very useful.
Here is a geometric proof of the sine addition formula. The proof also shows how someone could have discovered it.
Proof
editWe want to prove:
About the Diagram
editFirst, a word about the diagram used in the proof. How on earth would you come up with a diagram like that?
Well,
- We need a diagram with right triangles and we need to show an angle of , so having is a must.
- We want to express the lengths in this triangle in terms of lengths of two right triangles, one with angle and one with angle , so adding points like and is essential.
- Having got that far we could start trying to solve the problem, and we'd find we ran into a problem when calculating the distance . That's why we split into and . We can calculate the distance . It is the same length as . Also is a length we can calculate using Soh-Cah-Toa.
Be aware that there is nothing really special about the diagram we chose. It's possible, for example, to calculate using a diagram where the right triangle has its right angle at rather than at . You might like to try that.
We've chosen this digram and this lettering because it is exactly the same as used in the Khan Academy video on proving addition formula for sine so if you have trouble with the proof presented here, you can follow it on video instead.
Video Link
editThere is a video of the proof which may be easier to follow at the Khan Academy.
The Proof
edit
First check that the really is the same as . That's going to be important to the proof. We're just using the fact that angles in a triangle add up to 180° to make that check, noting that we know the 90 degree angles.
Now an expression for . Here we're using Soh-Cah-Toa. We're going to be using Soh-Cah-Toa a lot.
Looking at the diagram we can replace by and we also have so:
Let's work out another way to express and another way to express . You'll need to look at the diagram to see which triangles we are using.
|
An expression for and so |
An expression for and so |
Putting it all Together
editThe 's cancel.
We're done!
Exercises
edit|
Exercise: Make one of the sides 'one' When we drew the diagram we said nothing about its size. That means we could still choose to make one of the sides be of whatever length we like. We can do this for just one edge. Once we've done that all the other sides lengths are determined. Fixing one length to be a nice value can shorten the proof. So, let us decide that is 1 km. Actually we'll not worry about the units whether km, m or cm and just write '1'. is a right triangle and: Your task is to simplify the entire proof of the addition formula by replacing the lengths like with the actual values assuming that we've set . You're effectively removing and multiplication and division by from the proof. It should become a lot shorter and clearer. You should also mark up the lengths on the diagram, assuming . |
|
Exercise: Use a different diagram Read the description About the Diagram of how the diagram was constructed again. Make your own diagram that is different to the one shown, with right angles in different places to the diagram shown, and do the proof using it instead.
|
Multiple-Angle and Product-to-sum Formulas
Double angle formulae for cos and sine:
What Are the Double-Angle Formulae?
editThe Double-Angle formulas express the cosine and sine of twice an angle in terms of the cosine and sine of the original angle. We are going to derive them from the addition formulas for sine and cosine. The formulae are:
and
It is well worth practising the derivation so that you can do it quickly and easily. Then you will not need to remember the formulae, since you can get them quickly from the addition formulas for sine and cosine. It is also good to practice the derivation because being more fluent with the algebra will make you better at other algebra used with trigonometry.
|
Exercise: Check these Make Sense Did we make a typo in these formulae? Check they at least make sense.
|
|
Example: Half Angle formula for Cosine If we put we immediately get Check it. Do you agree? Or rearranging: So, if we know the cosine of (we do, it is zero), we can compute the cosine of and and and so on. |
Proofs for Double Angle Formulae
editWe'll prove the double angle formulae from the addition formulae. Recall that:
Putting in the above formula yields:
So:
Compare this with the "Pythagorean Theorem" expressed in terms of sine and cosine. Notice the double angle formula above has a minus not a plus, otherwise it would be saying , which would mean cos was 1 for all values of t, which we know is not true.
In terms of just cosine or just sine
editThe formula
isn't yet quite where we want it. We want to get rid of the sine term and express it all in terms of cosine. To do that we use the disguised "Pythagorean Theorem".
which is the same as:
so
so
which is what we wanted.
We could, if we had preferred, have used the disguised Pythagorean theorem to replace the in terms of
|
Exercise: Double angle cosine formula in terms of sine. Do that now, in other words express: in terms of
|
Double angle formula for sine
editNow we will get the double angle formula for sine, this time using the addition formula for sine.
Check that we've quoted the addition formula correctly, and then put in the above
So:
Unlike the formula for cosine the substitutions to get just in terms of would involve square roots, so we're not going to do that. The above formula is usually the nicest form to work with.
Treble and Higher Angles
editUsing the above procedures twice, and the Pythagorean theorem where appropriate, we find
By repeating the procedure, we can find formulae for and for any integer n. The formulas do however get rather long.
It is not really worthwhile remembering these formulae. They are not used often, and can either be looked up in tables of formulae or calculated when you need them. It is quite good for practising algebra to derive them yourself, so....
|
Exercise: Treble angle formulas for sine and cosine Derive the formulas for and yourself. |
Double and Treble Angles for Tangents
editBy using , it can be worked out that:
Like the formulas for and , these formulae aren't often useful, but again it is good to be able to work them out yourself.
|
Exercise: Multiple angle formulae for tan Derive the formulas for and yourself.
|
Additional Topics in Trigonometry
editLaw of Sines
editOoops. I should probably lose alpha beta and gamma from these diagrams |
For any triangle with vertices corresponding angles and corresponding opposite side lengths , the Law of Sines states that
Each of these expressions is also equal to the diameter of the triangle's circumcircle (the circle that passes through the points ). The law can also be written in terms of the reciprocals:
Proof
editDropping a perpendicular from vertex to intersect (or extended) at splits this triangle into two right-angled triangles and . We can calculate the length of the altitude in two different ways:
- Using the triangle AOC gives
- ;
- and using the triangle BOC gives
- .
- Eliminate from these two equations:
- .
- Rearrange to obtain
By using the other two perpendiculars the full law of sines can be proved. QED.
Application
editThis formula can be used to find the other two sides of a triangle when one side and the three angles are known. (If two angles are known, the third is easily found since the sum of the angles is .) See Solving Triangles Given ASA. It can also be used to find an angle when two sides and the angle opposite one side are known.
Area of a triangle
editThe area of a triangle may be found in various ways. If all three sides are known, use Heron's theorem.
If two sides and the included angle are known, consider the second diagram above. Let the sides and , and the angle between them be known. The terms /alpha and /gamma are variables represented by Greek alphabet letters, and these are commonly used interchangeably in trigonometry just like English variables x, y, z, a, b, c, etc. From triangle , the altitude is so the area is .
If two angles and the included side are known, again consider the second diagram above. Let the side and the angles and be known. Let . Then
Thus
- .
Law of Cosines
editLaw of Cosines
editThe Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:[1]
where is the angle between sides and .
Does the formula make sense?
editThis formula had better agree with the Pythagorean Theorem when .
So try it...
When ,
The and the formula reduces to the usual Pythagorean theorem.
Permutations
editFor any triangle with angles and corresponding opposite side lengths , the Law of Cosines states that
Proof
editDropping a perpendicular from vertex to intersect (or extended) at splits this triangle into two right-angled triangles and , with altitude from side .
First we will find the lengths of the other two sides of triangle in terms of known quantities, using triangle .
Side is split into two segments, with total length .
- has length
- has length
Now we can use the Pythagorean Theorem to find , since .
The corresponding expressions for and can be proved similarly.
The formula can be rearranged:
and similarly for and .
Applications
editThis formula can be used to find the third side of a triangle if the other two sides and the angle between them are known. The rearranged formula can be used to find the angles of a triangle if all three sides are known. See Solving Triangles Given SAS.
Notes
edit- ↑ Lawrence S. Leff (2005-05-01). cited work. Barron's Educational Series. p. 326. ISBN 0764128922.
Solving Triangles
editOne of the most common applications of trigonometry is solving triangles—finding missing sides and/or angles given some information about a triangle. The area of the triangle may also be required.
We can reconstruct the triangle given:
- ASA Angle-Side-Angle (see illustration below).
- AAS Angle-Angle-Side (see later on this page).
- SAS Side-Angle-Side (see next page).
- SSA Side-Side-Angle (later in this book). In the SSA case we may have one, two or no possible solutions.
Given ASA (Side and angles at each end of that side)
edit- Given two angles, we can find the third angle (since the sum of the measures of the three angles in a triangle is .
The missing angle, is given by:
- Knowing all three angles and one side, we can use the Law of Sines to find the missing sides.
In the illustration if the side we are given is the base and has length , then the side opposite the angle has length given by:
|
Check This
Now is also a good time to check that you can derive the law of sines for yourself. If given a problem triangle like this one in an exam, you might be asked both to find its missing sides and to derive the law of sines. |
- The area may then be found from Heron's Formula, or more easily by the formulae given in Law of Sines.
Given AAS (one side and two other angles)
editAgain we can work out the missing angle, since they sum to . From there on we have the same information as after the first step in the ASA case.
Exercises
edit|
Exercise 1: Easy angles I A triangle has:
|
|
Exercise 2: Easy angles II A triangle has:
|
|
Exercise 3: Similar/Congruent? Are these two triangles in Exercise 1 and Exercise 2:
|
Vectors in the Plane
editIn practice, one of the most useful applications of trigonometry is in calculations related to vectors, which are frequently used in Physics. A vector is a quantity which has both magnitude (such as three or eight) and direction (such as north or 30 degrees south of east). It is represented in diagrams by an arrow, often pointing from the origin to a specific point.
A plane vector can be expressed in two ways -- as the sum of a horizontal vector of magnitude and a vertical vector of magnitude , or in terms of its angle and magnitude (or simply A). These two methods are called "rectangular" and "polar" respectively.
Rectangular to Polar conversion
editFor simplicity, assume is in the first quadrant and has x-component and y-component (which will necessarily be positive). Given these components, we want to find the angle and the magnitude .
If we draw all three of these vectors, they form a right triangle. It is easy to see that , or (A vector with an angle of zero is defined to be pointing directly to the right.) Furthermore, by the Pythagorean Theorem, , or .
Polar to Rectangular conversion
editThis is essentially the same problem as above, but in reverse. Here, and are known and we want to calculate the values of and .
Using the same triangle as above, we can see that , or . Also, , or .
Review of conversions
editVectors and Dot Products
edit
Consider the vectors U and V (with respective magnitudes |U| and |V|). If those vectors enclose an angle θ then the dot product of those vectors can be written as:
If the vectors can be written as:
then the dot product is given by:
For example,
and
We can interpret the last case by noting that the product is zero because the angle between the two vectors is 90 degrees.
Since
and
this means that
Trigonometric Form of the Complex Number
edit
where
- i is the imaginary number
- the modulus
- the argument is the angle formed by the complex number on a polar graph with one real axis and one imaginary axis. This can be found using the right angle trigonometry for the trigonometric functions.
This is sometimes abbreviated as and it is also the case that (provided that is in radians). The latter identity is called Euler's formula.
Euler's formula can be used to prove DeMoivre's formula: This formula is valid for all values of n, real or complex.
Trigonometry References
editTrigonometric Unit Circle and Graph Reference
editThe unit circle is a commonly used tool in trigonometry because it helps the user to remember the special angles and their trigonometric functions. The unit circle is a circle drawn with its center at the origin of a graph(0,0), and with a radius of 1. All angles are measured starting from the x-axis in quadrant one and may go around the unit circle any number of degrees. Points on the outside of the circle that are in line with the terminal (ending) sides of the angles are very useful to know, as they give the trigonometric function of the angle through their coordinants. The format is (cos, sin).
Note that in trigonometry, an angle can be of any size, positive or negative. An angle larger than 360º means that you have gone round the circle more than once.
Trigonometric Formula Reference
edit|
Exercise: Remembering Formulae Cover the right hand side of each formula, and use the information about remembering formulae from the previous page to get the right hand side. |
Principal Trig Relationships
editThe following identities give relationships between the trigonometric functions.
Pythagoras related
edit|
Worked Example: The cot formula is missing One formula is missing. By dividing the by or by we can get two other formulae. The missing formula is obtained by dividing through by The missing formula is: |
Periodicity
editFour trigonometric functions are periodic:
Two trigonometric functions are periodic:
Angle Sums
editFormulae involving sums of angles are as follows:
Multiple Angle Formulae
editSubstituting gives the double angle formulae
Substituting gives
These can be obtained by putting in the addition formula.
This can also be obtained from the angle sums formula.
Trigonometric functions of some closely related angles
editThis list may duplicate some of the periodicity formulas above, but all the formulas are given for the sake of completeness. Angles are expressed in degrees rather than radians. Similar relations for cot, sec and cosec follow immediately from the definitions of these functions; just replace sin by cosec, cos by sec and tan by cot (and vice versa).
sin(x)
editcos(x)
edittan(x)
edit|
Exercise: Radians Rewrite the above formulas using radians. |
Trigonometric Identities Reference
editTriangle Identities
editIn addition to the Law of Sines, the Law of Cosines, and the Law of Tangents, there are numerous other identities that apply to the three angles A, B, and C of any triangle (where A+B+C=180° and each of A, B, and C is greater than zero). Some of the most notable ones follow:
Pythagoras
editThese are all direct consequences of Pythagoras's theorem.
Sum/Difference of angles
editProduct to Sum
editSum and difference to product
edit- , where and
Multiple angle
editThese are all direct consequences of the sum/difference formulae
Half angle
editIn cases with , the sign of the result must be determined from the value of . These derive from the formulae.
Power Reduction
editEven/Odd
editCalculus
editNatural Trigonometric Functions of Primary Angles
editNote: Some values in the table are given in forms that include a radical in the denominator — this is done both to simplify recognition of reciprocal pairs and because the form given in the table is simpler in some sense. Note also that all absolute values of trigonometric functions for remarkable points that are listed in this table are contained in the first quadrant (from 0 to 90° or radians, inclusive); all others are deduced by simple symmetries with the horizontal or vertical axis, or by swapping axes (on the trigonometric circle) so that one trigonometric function is also swapped with its co-function.
| (positive) | (negative) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| (degrees) | (radians) | (degrees) | (radians) | ||||||
| not defined |
not defined |
||||||||
| not defined |
not defined |
||||||||
| not defined |
not defined |
||||||||
| not defined |
not defined |
||||||||
| not defined |
not defined |
||||||||
Notice that for certain values of , the tangent, cotangent, secant, and cosecant functions are undefined. This is because these functions are defined as , , , and , respectively. Since an expression is undefined if it contains division by 0, the functions are therefore undefined at angle measures where the denominator (the sine or cosine of , depending on the trigonometric function) is equal to 0. For example, the tangent function for 90º ( radians) is equivalent to , or , which is an undefined value.












































![{\displaystyle \left[0,{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef281b69aa2a6b45a6bf42776cacf8b06be2b79)




































![{\displaystyle {\begin{matrix}&\mathrm {domain} &\mathrm {range} \\\mathrm {sine} &\mathbb {R} &[-1,1]\\\mathrm {cosine} &\mathbb {R} &[-1,1]\\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55eef5281aa09ec71c6b410c47f45d501dcdb669)




























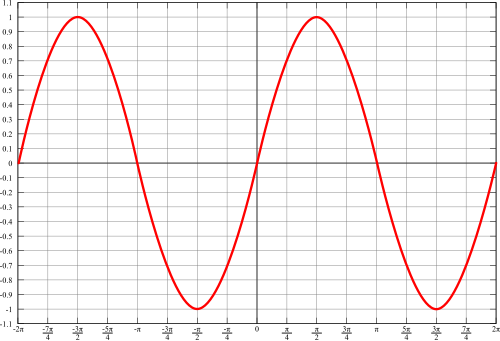
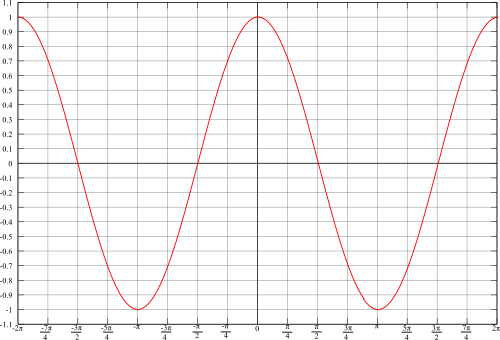


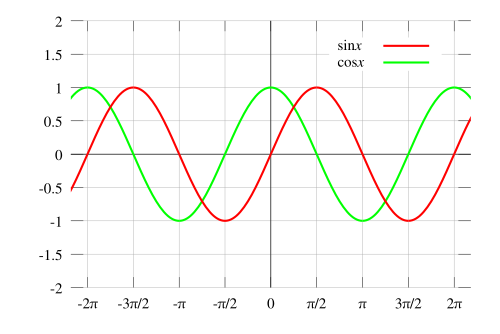



















































![{\displaystyle \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2052f9d4a9c6a14f6db2e4bcd2606bce26d720d)
![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)


























![{\displaystyle x={\sqrt {c_{1}^{2}+c_{2}^{2}}}\left[\sin \left(\phi +{\sqrt {\frac {k}{m}}}t\right)+\sin \left(\phi -{\sqrt {\frac {k}{m}}}t\right)\right]+{\sqrt {c_{1}^{2}+c_{2}^{2}}}\left[\sin \left({\sqrt {\frac {k}{m}}}t+\phi \right)+\sin \left({\sqrt {\frac {k}{m}}}t-\phi \right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cee4fb916123b6b6544e972abb150125aeee0c5)




















































































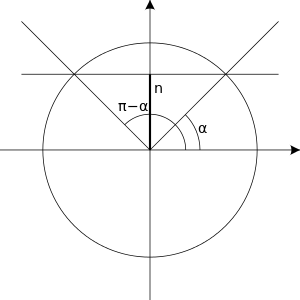



![{\displaystyle {\begin{matrix}x=\alpha +2k\pi \\x=\pi -\alpha +2k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1a3e9f50511c58a1b5da92a54ebaa528586f4b0)








![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)












![{\displaystyle {\begin{matrix}x=\pm \alpha +2k\pi \\\alpha \in [0,\pi ]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb327bcece984447ffb90d738e9f5c2246d7375d)







![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/091023c5ebe89e390dc7b3c08dc2aafd52f739cb)




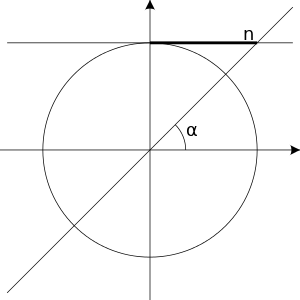

![{\displaystyle {\begin{matrix}x=\alpha +k\pi \\\alpha \in \left[0;\pi \right]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a09654bc73208cf0114b0bbebf26b68271c20ad0)











































































































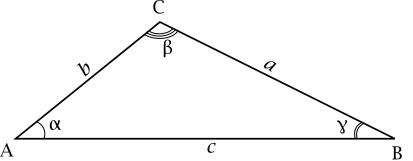

























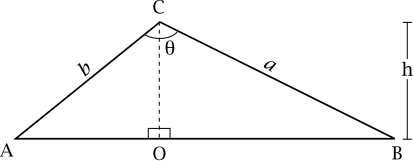














































































































































![{\displaystyle \sin ^{2}(4x)=16{\Big [}\sin ^{2}(x)-5\sin ^{4}(x)+8\sin ^{6}(x)-4\sin ^{8}(x){\Big ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/598b3543e3748f907f04fd36aeca7b182385ca5c)























![{\displaystyle {\frac {d}{dx}}{\big [}\sin(x){\big ]}=\cos(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e0926652b30841b3f9411fa26d6ff94ef0695d9)
![{\displaystyle {\frac {d}{dx}}{\big [}\cos(x){\big ]}=-\sin(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee6354b64afce92f2b1cadb5a495f5e1c88ceb25)
![{\displaystyle {\frac {d}{dx}}{\big [}\tan(x){\big ]}=\sec ^{2}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2876ba2de800a057c9e660f9ad76ac8deea0b3b)
![{\displaystyle {\frac {d}{dx}}{\big [}\sec(x){\big ]}=\sec(x)\tan(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da5289ee96dbb8faf5f9bf77d6ac714b9e34d464)
![{\displaystyle {\frac {d}{dx}}{\big [}\csc(x){\big ]}=-\csc(x)\cot(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3d9c7bf9123ab9d63656dff8df61248a3c4090c)
![{\displaystyle {\frac {d}{dx}}{\big [}\cot(x){\big ]}=-\csc ^{2}(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efd88e218e5cfb4d074b84f856586ee308dad192)






























































































































































