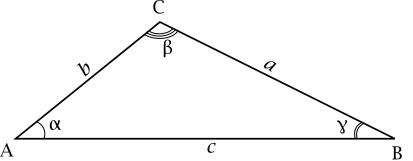
Trigonometry/Law of Sines

For any triangle with vertices $A,B,C$ corresponding angles $A,B,C$ and corresponding opposite side lengths $a,b,c$ , the Law of Sines states that

${\frac {a}{\sin(A)}}={\frac {b}{\sin(B)}}={\frac {c}{\sin(C)}}$

Each of these expressions is also equal to the diameter of the triangle's circumcircle (the circle that passes through the points $A,B,C$). The law can also be written in terms of the reciprocals:

${\frac {\sin(A)}{a}}={\frac {\sin(B)}{b}}={\frac {\sin(C)}{c}}$

Proof

Dropping a perpendicular $OC$ from vertex $C$ to intersect $AB$ (or $AB$ extended) at $O$ splits this triangle into two right-angled triangles $AOC$ and $BOC$ . We can calculate the length $h$ of the altitude $OC$ in two different ways:

• Using the triangle AOC gives

$h=b\sin(A)$ ;

• and using the triangle BOC gives

$h=a\sin(B)$ .

• Eliminate $h$ from these two equations:

$a\sin(B)=b\sin(A)$ .

• Rearrange to obtain

${\frac {a}{\sin(A)}}={\frac {b}{\sin(B)}}$

By using the other two perpendiculars the full law of sines can be proved. QED.

Application

This formula can be used to find the other two sides of a triangle when one side and the three angles are known. (If two angles are known, the third is easily found since the sum of the angles is $180^{\circ }$ .) See Solving Triangles Given ASA. It can also be used to find an angle when two sides and the angle opposite one side are known.

Area of a triangle

The area of a triangle may be found in various ways. If all three sides are known, use Heron's theorem.

If two sides and the included angle are known, consider the second diagram above. Let the sides $b$ and $c$ , and the angle between them $\alpha$ be known. The terms /alpha and /gamma are variables represented by Greek alphabet letters, and these are commonly used interchangeably in trigonometry just like English variables x, y, z, a, b, c, etc. From triangle $ACO$ , the altitude $h=CO$ is $b\sin(\alpha )$ so the area is ${\frac {bc\sin(\alpha )}{2}}$ .

If two angles and the included side are known, again consider the second diagram above. Let the side $c$ and the angles $\alpha$ and $\gamma$ be known. Let $AO=x$ . Then

${\frac {x}{h}}=\tan(\alpha ){\text{ ; }}{\frac {c-x}{h}}=\tan(\gamma ){\text{ ; adding these, }}{\frac {c}{h}}=\tan(\alpha )+\tan(\gamma )$

Thus

$h={\frac {c}{\tan(\alpha )+\tan(\gamma )}}{\text{ so area }}={\frac {c^{2}}{2{\bigl (}\tan(\alpha )+\tan(\gamma ){\bigr )}}}$ .