Fractals/moebius

Möbius transformation is an example of plane transformation

Riemann sphere

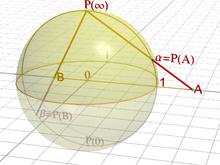
definition

A Möbius transformation of extended complex plane ${\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}$ is a rational function f of the form

$f(z)={\frac {az+b}{cz+d}}$

of one complex variable z.

Here the coefficients a, b, c, d and the result w are complex numbers satisfying

$ad-bc\neq 0$

$w=f(z)={\frac {az+b}{cz+d}}$

Representation or form

• function
• matrix

Function

$f(z)={\frac {az+b}{cz+d}}$

$f\ \colon z\to w$

$w=f(z)$

Matrix

In matrix form by using homogeneous coordinates:

$M=\left({\begin{matrix}{\begin{array}{cc}a&b\\c&d\end{array}}\end{matrix}}\right)\,$

$w=\left({\begin{matrix}{\begin{array}{c}w\\1\end{array}}\end{matrix}}\right)=\left({\begin{matrix}{\begin{array}{cc}a&b\\c&d\end{array}}\end{matrix}}\right)\left({\begin{matrix}{\begin{array}{c}z\\1\end{array}}\end{matrix}}\right)=\left({\begin{matrix}{\begin{array}{c}az+b\\cz+d\end{array}}\end{matrix}}\right)\,$

Matrix M is a square 2x2 invertible matrix

Examples

• Transforms using Complex Numbers
  • Moebius transformation
    • Paper: Squares that Look Round: Transforming Spherical Images by Saul Schleimer Henry Segerman and Shadertoy : Spherical Images by soma_arc and python code Henry Segerman
• Moebius transformation in mandelbrot-graphics library
• Mathematics of Kleinian Group Fractals by hiddendimension
• Generalized circles and Möbius transformations by Stéphane Laurent
• Projective Transformation and Mobius Transformation by Tadao Ito

simple

The following simple transformations are also Möbius transformations:

• $f(z)=z\quad (a=1,b=0,c=0,d=1)$ is an identity
• $f(z)=z+b\quad (a=1,c=0,d=1)$ is a translation
• $f(z)=az\quad (b=0,c=0,d=1)$ is a combination of a homothety and a rotation.
  • If $|a|=1$ then it is a rotation
  • if $a\in \mathbb {R}$ then it is a homothety
• $f(z)=1/z\quad (a=0,b=1,c=1,d=0)$ inversion and reflection with respect to the real axis)

How to ...?

eigenvalue and eigenvector

A number $\lambda$ and a non-zero vector $v$ satisfying

$Mv=\lambda v$

are called an eigenvalue and an eigenvector of matrix M, respectively.

For dimensions 2 formulas involving radicals exist that can be used to find the eigenvalues. The eigenvalues can be found by using the quadratic formula:

$\lambda _{\pm }={\frac {{\rm {tr}}(M)\pm {\sqrt {{\rm {tr}}^{2}(M)-4\det(M)}}}{2}}.$

diagonalization

a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. In other words all off-diagonal elements are zero in a diagonal matrix.

the main diagonal of a matrix $A$ is the list of entries $A_{i,j}$ where $i=j$, here $a_{11},a_{22}$

the diagonalization of a matrix M gives a pair of matrices: D, P such that:

• D is diagonal (all elements not on the diagonal are 0)
• $M=PDP^{-1}$

For 2x2 matrices there is a simple closed form solution

Product with a scalar

If A is a matrix and c a scalar, then the matrices $c\mathbf {A}$ and $\mathbf {A} c$ are obtained by left or right multiplying all entries of A by c.

trace

The trace $\operatorname {tr}$ of a square 2x2 matrix $\mathbf {A}$

$\mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}}$

is the sum of its diagonal entries

$\operatorname {tr} (\mathbf {A} )=\sum _{i=1}^{2}a_{ii}=a_{11}+a_{22}$

So $\operatorname {tr} (\mathbf {M} )=a+d$

determinant

determinant $\operatorname {det}$ of matrix $\mathbf {M}$

$\operatorname {det} \mathbf {M} =\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}=ad-bc$

inverse

Mapping of generalised circles by inversion w=Sz=1/z (primitive Möbius-transform). Straight lines are mapped to circles/lines.

Inverse Möbius transformation

$\mathbf {M} ^{-1}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}^{-1}={\frac {1}{\operatorname {det} \mathbf {M} }}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}={\frac {1}{ad-bc}}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}$

$z={\frac {1}{\operatorname {det} \mathbf {M} }}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}{\begin{pmatrix}w\\1\end{pmatrix}}$

$z=f^{-1}(w)$.

interpolation

How to smootly interpolate between möbius transformations?

If you have two Möbius transformations represented as:

$f(z)={\frac {az+b}{cz+d}}$

$g(z)={\frac {pz+q}{rz+s}}$

where coefficients are complex numbers

$a,b,c,d,p,q,r,s,z\in \mathbb {C}$

Is it possible to derive a third function $h(z,t)$, where $t\in \mathbb {R}$ and $0\leq t\leq 1$, which "smoothly" interpolates between the transformations represented by $f(z)$ and $g(z)$?

The solution:

$h(z,t)=fe^{t\log(f^{-1}g)}=f\operatorname {exp} (t\log(f^{-1}g))$

Specifying a transformation by three points

Given a set of three distinct points z₁, z₂, z₃ on the one Riemann sphere ( let's call it z-sphere) and a second set of distinct points w₁, w₂, w₃ on the second sphere ( w-sphere) , there exists precisely one Möbius transformation f(z) with :

• $f(z_{i})=w_{i}$
• $f^{-1}(w)=z_{i}$

for i=1,2,3

Mapping to 0, 1, infinity

The Möbius transformation with an explicit formula :

$f(z)={\frac {(z-z_{1})(z_{2}-z_{3})}{(z-z_{3})(z_{2}-z_{1})}}$

maps :

• z₁ to w₁= 0
• z₂ to w₂= 1
• z₃ to w₃= ∞

the unit circle to the real axis - first method

Let's choose 3 z points on a circle :

• z₁= -1
• z₂= i
• z₃= 1

then the Möbius transformation will be :

$f(z)={\frac {(z+1)(i-1)}{(z-1)(i+1)}}$

Knowing that :

$i+1=-i(i-1)$

one can simplify this to :

$f(z)=i{\frac {z+1}{z-1}}$

In Maxima CAS one can do it :

(%i1) rectform((z+1)*(%i-1)/((z-1)*(%i+1)));
(%o1) (%i*(z+1))/(z−1)

where coefficients of the general form are :

$a=i$

$b=i$

$c=1$

$d=-1$

so inverse function can be computed using general form :

$f^{-1}(w)={\frac {dw-b}{-cw+a}}={\frac {-i-w}{i-w}}$

Lets check it using Maxima CAS :

(%i3) fi(w):=(-%i-w)/(%i-w);
(%o3) fi(w):=−%i−w/%i−w
(%i4) fi(0);
(%o4) −1
(%i5) fi(1);
(%o5) −%i−1/%i−1
(%i6) rectform(%);
(%o6) %i

Find how to compute it without symbolic computation program (CAS)  :

(%i3) fi(w):=(-%i-w)/(%i-w);
(%o3) fi(w):=−%i−w/%i−w
(%i8) z:x+y*%i;
(%o8) %i*y+x
(%i9) z1:fi(w);
(%o9) (−%i*y−x−%i)/(−%i*y−x+%i)
(%i10) realpart(z1);
(%o10) ((−y−1)*(1−y))/((1−y)^2+x^2)+x^2/((1−y)^2+x^2)
(%i11) imagpart(z1);
(%o11) (x*(1−y))/((1−y)^2+x^2)−(x*(−y−1))/((1−y)^2+x^2)
(%i13) ratsimp(realpart(z1));
(%o13) (y^2+x^2−1)/(y^2−2*y+x^2+1)
(%i14) ratsimp(imagpart(z1));
(%o14) (2*x)/(y^2−2*y+x^2+1)

2 steps of unrolling the main cardioid of Mandelbrot set: Moebius map and conformal map

Unrolled main cardioid of Mandelbrot set for periods 7-13

So using notation :

$z=x+yi=f^{-1}(w)$

one gets :

$x=\operatorname {Re} (z)=\operatorname {Re} (f^{-1}(w))={\frac {y^{2}+x^{2}-1}{y^{2}-2y+x^{2}+1}}$

$y=\operatorname {Im} (z)=\operatorname {Im} (f^{-1}(w))={\frac {2x}{y^{2}-2y+x^{2}+1}}$

It can be used for unrolling the Mandelbrot set components

the unit circle to the real axis - second method

Function :

$f(z)=i{\frac {z-1}{z+1}}$

sends the unit circle to the real axis :

• z=1 to w=0
• z=i to w=1
• z=-1 to $w=\infty$

Mapping to the imaginary axis

Function $f(z)={\frac {z-1}{z+1}}$ sends the unit circle to the imaginary axis.

visualisations

• mobius revealed by Mark McClure
• live demo by Tim Hutton
• Iterating the Möbius transformation by Tim Hutton

References

• moebius-transformation by Claude Heiland-Allen