Abstract Algebra/Printable version

Abstract Algebra

The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/Abstract_Algebra

Permission is granted to copy, distribute, and/or modify this document under the terms of the Creative Commons Attribution-ShareAlike 3.0 License.

Sets

Sets

In the so-called naive set theory, which is sufficient for the purpose of studying abstract algebra, the notion of a set is not rigorously defined. We describe a set as a well-defined aggregation of objects, which are referred to as members or elements of the set. If a certain object is an element of a set, it is said to be contained in that set. The elements of a set can be anything at all, but in the study of abstract algebra, elements are most frequently numbers or mathematical structures. The elements of a set completely determine the set, and so sets with the same elements as each other are equal. Conversely, sets which are equal contain the same elements.

For an element $x$ and a set $A$, we can say either $x\in A$, that is, $x$ is contained in $A$, or $x\not \in A$, that is, $x$ is not contained in $A$. To state that multiple elements $a,b,c,\ldots ,n$ are contained in $A$, we write $a,b,c,\ldots ,n\in A$.

The axiom of extensionality

Using this notation and the symbol $\rightarrow$, which represents logical implication, we can restate the definition of equality for two sets $A$ and $B$ as follows:

$A=B$ if and only if $x\in A\rightarrow x\in B$ and $x\in B\rightarrow x\in A$.

This is known as the axiom of extensionality.

Comprehensive notation

If it is not possible to list the elements of a set, it can be defined by giving a property that its elements are sole to possess. The set of all objects $x$ with some property $Q(x)$ can be denoted by $\{x:Q(x)\}$. Similarly, the set of all elements $x$ of a set $A$ with some property $Q(x)$ can be denoted by $\{x\in A:Q(x)\}$. The colon : here is read as "such that". The vertical bar | is synonymous with the colon in similar contexts. This notation will appear quite often in the rest of this book, so it is important for the readers to familiarize themselves with this now.

As an example of this notation, the set of integers can be written as $\mathbb {Z} =\{x:x{\text{ is an integer}}\}$, and the set of even integers can be written as $\{x\in \mathbb {Z} :x{\text{ is even}}\}$.

Set inclusion

For two sets $A$ and $B$, we define set inclusion as follows: $A$ is included in, or a subset of, $B$, if and only if every member of $A$ is a member of $B$. In other words,

$A\subseteq B\Leftrightarrow x\in A\rightarrow x\in B$

where the symbol $\subseteq$ denotes "is a subset of", and $\Leftrightarrow$ denotes "if and only if".

By the aforementioned axiom of extensionality, one finds that $A=B\Leftrightarrow A\subseteq B{\mbox{ and }}B\subseteq A$.

The empty set

One can define an empty set, written $\varnothing$, such that $\forall x(x\not \in \varnothing )$, where $\forall$ denotes universal quantification (read as "for all" or "for every"). In other words, the empty set is defined as the set which contains no elements. The empty set can be shown to be unique.

Since the empty set contains no elements, it can be shown to be a subset of every set. Similarly, no set but the empty set is a subset of the empty set.

Proper set inclusion

For two sets $A$ and $B$, we can define proper set inclusion as follows: $A$ is a proper subset of $B$ if and only if $A$ is a subset of $B$, and $A$ does not equal $B$. In other words, there is at least one member in $B$ not contained in $A$

$A\subset B\Leftrightarrow (A\subseteq B\land A\neq B)$,

where the symbol $\subset$ denotes "is a proper subset of" and the symbol $\land$ denotes logical and.

Cardinality of sets

The cardinality of a set $A$, denoted by $|A|$, can be said informally to be a measure of the number of elements in $A$. However, this description is only rigorously accurate for finite sets. To find the cardinality of infinite sets, more sophisticated tools are needed.

Set intersection

For sets $A$ and $B$, we define the intersection of $A$ and $B$ by the set $A\cap B$ which contains all elements which are common to both $A$ and $B$. Symbolically, this can be stated as follows:

$A\cap B=\{x\mid x\in A{\mbox{ and }}x\in B\}$.

Because every element of $A\cap B$ is an element of $A$ and an element of $B$, $A\cap B$ is, by the definition of set inclusion, a subset of $A$ and $B$.

If the sets $A$ and $B$ have no elements in common, they are said to be disjoint sets. This is equivalent to the statement that $A$ and $B$ are disjoint if $A\cap B=\emptyset$.

Set intersection is an associative and commutative operation; that is, for any sets $A$, $B$, and $C$, $(A\cap B)\cap C=A\cap (B\cap C)$ and $A\cap B=B\cap A$.

By the definition of intersection, one can find that $A\cap \emptyset =\emptyset$ and $A\cap A=A$. Furthermore, $A\subseteq B\Leftrightarrow A\cap B=A$.

One can take the intersection of more than two sets at once; since set intersection is associative and commutative, the order in which these intersections are evaluated is irrelevant. If $A_{i}$ are sets for every $i\in I$, we can denote the intersection of all $A_{i}$ by

$\bigcap _{i\in I}A_{i}=\{x\mid (\forall i\in I)x\in A_{i}\}$

In cases like this, $I$ is called an index set, and $A_{i}$ are said to be indexed by $I$.

In the case of $I=\{1,2,...,n\}$ one can either write $A_{1}\cap A_{2}\cap A_{3}\cap \cdots \cap A_{n}$ or

$\bigcap _{i=1}^{n}A_{i}$.

Set union

For sets $A$ and $B$, we define the union of $A$ and $B$ by the set $A\cup B$ which contains all elements which are in either $A$ or $B$ or both. Symbolically,

$A\cup B=\{x\mid x\in A{\mbox{ or }}x\in B\}$.

Since the union $A\cup B$ of sets $A$ and $B$ contains the elements of $A$ and $B$, $A\subseteq A\cup B$ and $B\subseteq A\cup B$.

Like set intersection, set union is an associative and commutative operation; for any sets $A$, $B$, and $C$, $(A\cup B)\cup C=A\cup (B\cup C)$ and $A\cup B=B\cup A$.

By the definition of union, one can find that $A\cup \emptyset =A\cup A=A$. Furthermore, $A\subseteq B\Leftrightarrow A\cup B=B$.

Just as with set intersection, one can take the union of more than two sets at once; since set union is associative and commutative, the order in which these unions are evaluated is irrelevant. Let $A_{i}$ be sets for all $i\in I$. Then the union of all the $A_{i}$ is denoted by

$\bigcup _{i\in I}A_{i}=\{x\mid (\exists i\in I)x\in A_{i}\}$

(Where $\exists$ may be read as "there exists".)

For the union of a finite number of sets $A_{1},A_{2},A_{3},\ldots ,A_{n}$, that is, $I=\{1,2,...,n\}$ one can either write $A_{1}\cup A_{2}\cup A_{3}\cup \cdots \cup A_{n}$ or abbreviate this as

$\bigcup _{i=1}^{n}A_{i}$.

Distributive laws

Set union and set intersection are distributive with respect to each other. That is,

$A\cap (B\cup C)=(B\cup C)\cap A=(A\cap B)\cup (A\cap C)$ and

$A\cup (B\cap C)=(B\cap C)\cup A=(A\cup B)\cap (A\cup C)$.

Cartesian product

The Cartesian product of sets $A$ and $B$, denoted by $A\times B$, is the set of all ordered pairs which can be formed with the first object in the ordered pair being an element of $A$ and the second being an element of $B$. This can be expressed symbolically as

$A\times B=\{(x,y)\mid x\in A{\mbox{ and }}y\in B\}$.

Since different ordered pairs result when one exchanges the objects in the pair, the Cartesian product is not commutative. The Cartesian product is also not associative. The following identities hold for the Cartesian product for any sets $A,B,C,D$:

$(A\cap B)\times (C\cap D)=(A\times C)\cap (B\times D)$,

$(A\cup B)\times (C\cup D)=(A\times C)\cup (A\times D)\cup (B\times C)\cup (B\times D)$,

$A\times (B\cap C)=(A\times B)\cap (A\times C)$,

$A\times (B\cup C)=(A\times B)\cup (A\times C)$.

The Cartesian product of any set and the empty set yields the empty set; symbolically, for any set $A$, $A\times \emptyset =\emptyset \times A=\emptyset$.

The Cartesian product can easily be generalized to the n-ary Cartesian product, which is also denoted by $\times$. The n-ary Cartesian product forms ordered n-tuples from the elements of $n$ sets. Specifically, for sets $A_{1},A_{2},A_{3},\ldots ,A_{n}$,

$A_{1}\times A_{2}\times A_{3}\times \cdots \times A_{n}=\{(x_{1},\ldots ,x_{n}):x_{i}\in A_{i}\}$.

This can be abbreviated as

$\prod _{i=1}^{n}A_{i}$.

In the n-ary Cartesian product, each $x_{i}$ is referred to as the $i$-th coordinate of $(x_{1},\ldots ,x_{n})$.

In the special case where all the factors are the same set $A$, we can generalize even further. Let $A^{\Omega }$ be the set of all functions $f\,:\,\Omega \rightarrow A$. Then, in analogy with the above, $A^{\Omega }$ is effectively the set of "$\Omega$-tuples" of elements in $A$, and for each such function $f$ and each $i\in \Omega$, we call $f(i)$ the $i$-th coordinate of $f$. As one might expect, in the simple case when $\Omega =\{1,2,...,n\}$ for an integer $n$, this construction is equivalent to $\prod _{i=1}^{n}A$, which we can abbreviate further as $A^{n}$. We also have the important case of $\Omega =\mathbb {N}$, giving rise to the set of all infinite sequences of elements of $A$, which we can denote by $A^{\infty }$. We will need this construction later, in particular when dealing with polynomial rings.

Disjoint union

Let $A$ and $B$ be any two sets. We then define their disjoint union, denoted $A\coprod B$ to be the following: First create copies $A^{\prime }$ and $B^{\prime }$ of $A$ and $B$ such that $A^{\prime }\cap B^{\prime }=\emptyset$. Then define $A\coprod B=A^{\prime }\cup B^{\prime }$. Notice that this definition is not explicit, like the other operations defined so far. The definition does not output a single set, but rather a family of sets. However, these are all "the same" in a sense which will be defined soon. In other words, there exists bijective functions between them.

Luckily, if a disjoint union is needed for explicit computation, one can easily be constructed, for example $A\coprod B=(\{0\}\times A)\cup (\{1\}\times B)$.

Set difference

The set difference, or relative set complement, of sets $A$ and $B$, denoted by $A\setminus B$, is the set of elements contained in $A$ which are not contained in $B$. Symbolically,

$A\setminus B=\{x\mid x\in A{\mbox{ and }}x\not \in B\}$.

By the definition of set difference, $A\setminus B\subseteq A$.

The following identities hold for any sets $A,B,C$:

$A\setminus B=A\Leftrightarrow A\cap B=\emptyset$,

$A\setminus B=\emptyset \Leftrightarrow A\subseteq B$,

$A\setminus B=A\setminus C\Leftrightarrow A\cap B=A\cap C$,

$A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C)$,

$A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)$,

$A\setminus (B\setminus C)=(C\cap A)\cup (A\setminus B)$,

$A\setminus \emptyset =A$,

$A\setminus A=\emptyset$,

$\emptyset \setminus A=\emptyset$.

The set difference of two Cartesian products can be found as $(A\times B)\setminus (C\times D)=[A\times (B\setminus D)]\cup [(A\setminus C)\times B]$.

The universal set and set complements

We define some arbitrary set $U$ for which every set under consideration is a subset of $U$ as the universal set, or universe. The complement of any set is then defined to be the set difference of the universal set and that set. That is, for any set $A\subseteq U$, the complement of $A$ is given by $A^{C}=U\setminus A$. The following identities involving set complements hold true for any sets $A$ and $B$:

De Morgan's laws for sets:

$(A\cup B)^{C}=A^{C}\cap B^{C}$,

$(A\cap B)^{C}=A^{C}\cup B^{C}$,

Double complement law:

$A^{CC}=A$,

Complement properties:

$A\cup A^{C}=U$,

$A\cap A^{C}=\emptyset$,

$\emptyset ^{C}=U$,

$U^{C}=\emptyset$,

$A\subseteq B\rightarrow B^{C}\subseteq A^{C}$.

The set complement can be related to the set difference with the identities $A\setminus B=A\cap B^{C}$ and $(A\setminus B)^{C}=A^{C}\cup B$.

Symmetric difference

For sets $A$ and $B$, the symmetric set difference of $A$ and $B$, denoted by $A\bigtriangleup B$ or by $A\ominus B$, is the set of elements which are contained either in $A$ or in $B$ but not in both of them. Symbolically, it can be defined as

$A\bigtriangleup B=\{x:(x\in A)\oplus (x\in B)\}.$

More commonly, it is represented as

$A\bigtriangleup B=(A\setminus B)\cup (B\setminus A)$ or as

$A\bigtriangleup B=(A\cup B)\setminus (A\cap B)$.

The symmetric difference is commutative and associative so that $A\bigtriangleup B=B\bigtriangleup A$ and $(A\bigtriangleup B)\bigtriangleup C=A\bigtriangleup (B\bigtriangleup C)$. Every set is its own symmetric-difference inverse, and the empty set functions as an identity element for the symmetric difference, that is, $A\bigtriangleup A=\emptyset$ and $A\bigtriangleup \emptyset =A$. Furthermore, $A\bigtriangleup B=\emptyset$ if and only if $A=B$.

Set intersection is distributive over the symmetric difference operation. In other words, $A\cap (B\bigtriangleup C)=(A\cap B)\bigtriangleup (A\cap C)$.

The symmetric difference of two set complements is the same as the symmetric difference of the two sets: $A^{C}\bigtriangleup B^{C}=A\bigtriangleup B$.

Notation for specific sets

Commonly-used sets of numbers in mathematics are often denoted by special symbols. The conventional notations used in this book are given below.

Natural numbers with 0: $\mathbb {N} _{0}=\{0,1,2,\ldots \}$ or $\mathbb {N} =\{0,1,2,\ldots \}$
Natural numbers without 0: $\mathbb {N} ^{*}=\{1,2,3,\ldots \}$
Integers: $\mathbb {Z} =\{0,\pm 1,\pm 2,\ldots \}$
Rational numbers: $\mathbb {Q} =\left\{{\frac {p}{q}}:p\in \mathbb {Z} {\mbox{ and }}q\in \mathbb {N} ^{*}\right\}$
Real numbers: $\mathbb {R}$
Complex numbers: $\mathbb {C}$

Equivalence relations and congruence classes

We often wish to describe how two mathematical entities within a set are related. For example, if we were to look at the set of all people on Earth, we could define "is a child of" as a relationship. Similarly, the $\geq$ operator defines a relation on the set of integers. A binary relation, hereafter referred to simply as a relation, is a binary proposition defined on any selection of the elements of two sets.

Formally, a relation is any arbitrary subset of the Cartesian product between two sets $X$ and $Y$ so that, for a relation $R$, $R\subseteq X\times Y$. In this case, $X$ is referred to as the domain of the relation and $Y$ is referred to as its codomain. If an ordered pair $(x,y)$ is an element of $R$ (where, by the definition of $R$, $x\in X$ and $y\in Y$), then we say that $x$ is related to $y$ by $R$. We will use $R(x)$ to denote the set

$\{y\in Y:(x,y)\in R\}$.

In other words, $R(x)$ is used to denote the set of all elements in the codomain of $R$ to which some $x$ in the domain is related.

Equivalence relations

To denote that two elements $x$ and $y$ are related for a relation $R$ which is a subset of some Cartesian product $X\times X$, we will use an infix operator. We write $x\sim y$ for some $x,y\in X$ and $(x,y)\in R$.

There are very many types of relations. Indeed, further inspection of our earlier examples reveals that the two relations are quite different. In the case of the "is a child of" relationship, we observe that there are some people A,B where neither A is a child of B, nor B is a child of A. In the case of the $\geq$ operator, we know that for any two integers $m,n\in Z$ exactly one of $m\geq n$ or $n>m$ is true. In order to learn about relations, we must look at a smaller class of relations.

In particular, we care about the following properties of relations:

• Reflexivity: A relation $R\subseteq X\times X$ is reflexive if $a\sim a$ for all $a\in X$.
• Symmetry: A relation $R\subseteq X\times X$ is symmetric if ${a\sim b}\implies {b\sim a}$ for all $a,b\in X$.
• Transitivity: A relation $R\subseteq X\times X$ is transitive if ${{a\sim b}\wedge {b\sim c}}\implies {a\sim c}$ for all $a,b,c\in X$.

One should note that in all three of these properties, we quantify across all elements of the set $X$.

Any relation $R\subseteq X\times X$ which exhibits the properties of reflexivity, symmetry and transitivity is called an equivalence relation on $X$. Two elements related by an equivalence relation are called equivalent under the equivalence relation. We write $a\sim _{R}b$ to denote that $a$ and $b$ are equivalent under $R$. If only one equivalence relation is under consideration, we can instead write simply $a\sim b$. As a notational convenience, we can simply say that $\sim$ is an equivalence relation on a set $X$ and let the rest be implied.

Example: For a fixed integer $p$, we define a relation $\sim _{p}$ on the set of integers such that $a\sim _{p}b$ if and only if $a-b=kp$ for some $k\in Z$. Prove that this defines an equivalence relation on the set of integers.

Proof:

• Reflexivity: For any $a\in X$, it follows immediately that $a-a=0=0p$, and thus $a\sim _{p}a$ for all $a\in G$.
• Symmetry: For any $a,b\in X$, assume that $a\sim _{p}b$. It must then be the case that $a-b=kp$ for some integer $k$, and $b-a=(-k)p$. Since $k$ is an integer, $-k$ must also be an integer. Thus, ${a\sim _{p}b}\implies {b\sim _{p}a}$ for all $a,b\in G$.
• Transitivity: For any $a,b,c\in X$, assume that $a\sim _{p}b$ and $b\sim _{p}c$. Then $a-b=k_{1}p$ and $b-c=k_{2}p$ for some integers $k_{1},k_{2}$. By adding these two equalities together, we get ${(a-b)+(b-c)=(k_{1}p)+(k_{2}p)}\Leftrightarrow {a-c=(k_{1}+k_{2})p}$, and thus $a\sim _{p}c$.

Q.E.D.

Remark. In elementary number theory we denote this relation $a\equiv b({\text{mod }}p)$ and say a is equivalent to b modulo p.

Equivalence classes

Let $\sim$ be an equivalence relation on $X$. Then, for any element $a\in X$ we define the equivalence class of $a$ as the subset $\left[a\right]\subseteq X$ given by

$\left[a\right]=\left\{b\in X|a\sim b\right\}$

Theorem: $b\in \left[a\right]\implies \left[b\right]=\left[a\right]$

Proof: Assume $b\in \left[a\right]$. Then by definition, $a\sim b$.

• We first prove that $\left[b\right]\subseteq \left[a\right]$. Let $p$ be an arbitrary element of $\left[b\right]$. Then $p\sim b$ by definition of the equivalence class, and $p\sim a$ by transitivity of equivalence relations. Thus, ${p\in \left[b\right]}\implies {p\in \left[a\right]}$ and $\left[b\right]\subseteq \left[a\right]$.
• We now prove that $\left[a\right]\subseteq \left[b\right]$ Let $q$ be an arbitrary element of $\left[a\right]$. Then, by definition $q\sim a$. By transitivity, $q\sim b$, so $q\in \left[b\right]$. Thus, ${q\in \left[a\right]}\implies {q\in \left[b\right]}$ and $\left[a\right]\subseteq \left[b\right]$.

As $\left[a\right]\subseteq \left[b\right]$ and as $\left[b\right]\subseteq \left[a\right]$, we have $\left[b\right]=\left[a\right]$.

Q.E.D.

Partitions of a set

A partition of a set $X$ is a disjoint family of sets $X_{i}$, $i\in I$, such that $\bigcup _{i\in I}X_{i}=X$.

Theorem: An equivalence relation $\sim$ on $X$ induces a unique partition of $X$, and likewise, a partition induces a unique equivalence relation on $X$, such that these are equivalent.

Proof: (Equivalence relation induces Partition): Let $P$ be the set of equivalence classes of $\sim$. Then, since $a\in [a]$ for each $a\in X$, $\cup P=X$. Furthermore, by the above theorem, this union is disjoint. Thus the set of equivalence relations of $\sim$ is a partition of $X$.

(Partition induces Equivalence relation): Let $X_{i}\,,\,i\in I$ be a partition of $X$. Then, define $\sim$ on $X$ such that $a\sim b$ if and only if both $a$ and $b$ are elements of the same $X_{i}$ for some $i\in I$. Reflexivity and symmetry of $\sim$ is immediate. For transitivity, if $a,b\in X_{i}$ and $b,c\in X_{i}$ for the same $i\in I$, we necessarily have $a,c\in X_{i}$, and transitivity follows. Thus, $\sim$ is an equivalence relation with $X_{i}\,,\,i\in I$ as the equivalence classes.

Lastly obtaining a partition $P$ from $\sim$ on $X$ and then obtaining an equivalence equation from $P$ obviously returns $\sim$ again, so $\sim$ and $P$ are equivalent structures.

Q.E.D.

Quotients

Let $\sim$ be an equivalence relation on a set $X$. Then, define the set $X/\sim$ as the set of all equivalence classes of $X$. In order to say anything interesting about this construction we need more theory yet to be developed. However, this is one of the most important constructions we have, and one that will be given much attention throughout the book.

Functions

Definition

A function $\operatorname {f}$ is a triplet $(A,B,G)$ such that:

• $A$ is a set, called the domain of $\operatorname {f}$
• $B$ is a set, called the codomain of $\operatorname {f}$
• $G$ is a subset of $A\times B$, called the graph of $\operatorname {f}$

In addition the following two properties hold:

1. $\forall x\in A,\exists y\in B\mid (x,y)\in G$.
2. $\forall x\in A,y\in B,y'\in B{\mbox{, then }}(x,y)\in G{\mbox{ and }}(x,y')\in G\Rightarrow y=y'$.

$\forall x\in A$ we write $\operatorname {f} (x)$ for the unique $y\in B$ such that $(x,y)\in G$.

We say that $\operatorname {f}$ is a function from $A$ to $B$, which we write:

$\operatorname {f} :A\rightarrow B$

Example

Let's consider the function from the reals to the reals which squares its argument. We could define it like this:

$\operatorname {f} :\mathbb {R} \rightarrow \mathbb {R}$

$\operatorname {f} :x\mapsto x^{2}$

Remark

As you see in the definition of a function above, the domain and codomain are an integral part of the definition. In other words, even if the values of $\operatorname {f} (x)$ don't change, changing the domain or codomain changes the function.

Let's look at the following four functions.

The function:

$\operatorname {f_{1}} :\mathbb {R} \rightarrow \mathbb {R}$

$\operatorname {f_{1}} :x\mapsto x^{2}$

is neither injective nor surjective (these terms will be defined later).

The function:

$\operatorname {f_{2}} :\mathbb {R} \rightarrow \mathbb {R} _{\geq 0}$

$\operatorname {f_{2}} :x\mapsto x^{2}$

is not injective but surjective.

The function:

$\operatorname {f_{3}} :\mathbb {R} _{\geq 0}\rightarrow \mathbb {R}$

$\operatorname {f_{3}} :x\mapsto x^{2}$

is injective but not surjective.

The function:

$\operatorname {f_{4}} :\mathbb {R} _{\geq 0}\rightarrow \mathbb {R} _{\geq 0}$

$\operatorname {f_{4}} :x\mapsto x^{2}$

is injective and surjective

As you see, all four functions have the same mapping but all four are different. That's why just giving the mapping is insufficient; a function is only defined if its domain and codomain are known.

Image and preimage

For a set $E$, we write ${\mathcal {P}}(E)$ for the set of subsets of $E$.

Let $\operatorname {f} :A\rightarrow B$. We will now define two related functions.

The image function:

$\operatorname {f} :{\mathcal {P}}(A)\rightarrow {\mathcal {P}}(B),S\subseteq A\mapsto \{\operatorname {f} (x)\mid x\in S\}$

The preimage function:

$\operatorname {f^{-1}} :{\mathcal {P}}(B)\rightarrow {\mathcal {P}}(A),T\subseteq B\mapsto \{x\in A\mid \operatorname {f} (x)\in T\}$

Note that the image and preimage are written respectively like $\operatorname {f}$ and its inverse (if it exists). There is however no ambiguity because the domains are different. Note also that the image and preimage are not necessarily inverse of one another. (See the section on bijective functions below).

We define $\operatorname {Im} _{\operatorname {f} }:=\operatorname {f} (A)$, which we call the image of $\operatorname {f}$.

For any $y\in B$, we call $\operatorname {f^{-1}} (\{y\})$ the support of $y$.

Proposition: Let $\operatorname {f} :A\rightarrow B$. Then

1. $\forall S\subseteq A,S\subseteq f^{-1}(f(S))$
2. $\forall T\subseteq B,f(f^{-1}(T))\subseteq T$

Example

Let's take again the function:

$\operatorname {f} :\mathbb {R} \rightarrow \mathbb {R}$

$\operatorname {f} :x\mapsto x^{2}$

Let's consider the following examples:

$\operatorname {f^{-1}} (\{4\})=\{-2,2\}$

$\operatorname {f^{-1}} (\mathbb {R} _{<0})=\emptyset$

$\operatorname {f} (\mathbb {R} _{\geq 0})=\mathbb {R} _{\geq 0}$

Further definitions

Let $\operatorname {f} :B\rightarrow C$ and $\operatorname {g} :A\rightarrow B$. We define $\operatorname {f} \circ \operatorname {g} :A\rightarrow C$ by $(\operatorname {f} \circ \operatorname {g} )(x):=\operatorname {f} (\operatorname {g} (x))$, which we call the composition of $\operatorname {f}$ and $\operatorname {g}$.

Let $A$ be a set. We define the identity function on A as

$\operatorname {id_{A}} :A\rightarrow A,x\mapsto x$

Properties

Definition: A function $\operatorname {f} :A\rightarrow B$ is injective if

$\forall x\in A,x'\in A,\operatorname {f} (x)=\operatorname {f} (x')\Rightarrow x=x'$

Lemma: Consider a function $\operatorname {f} :A\rightarrow B$ and suppose $A\neq \emptyset$. Then $\operatorname {f}$ is injective if and only if there exists a function $\operatorname {g} :B\rightarrow A$ with $\operatorname {g} \circ \operatorname {f} =\operatorname {id_{A}}$.
Proof:
$'\Rightarrow '$:
Suppose $\operatorname {f}$ is injective. As $A\neq \emptyset$ let's define $m$ as an arbitrary element of $A$. We can then define a suitable function $\operatorname {g} :B\rightarrow A$ as follows:

$\operatorname {g} (y):=\left\{{\begin{array}{ll}{\mbox{the unique }}x\in A\mid \operatorname {f} (x)=y&{\text{, if }}y\in \operatorname {Im} _{\operatorname {f} }\\m&{\text{, else}}\\\end{array}}\right.$

It is now easy to verify that $\operatorname {g} \circ \operatorname {f} =\operatorname {id_{A}}$.
$'\Leftarrow '$:
Suppose there is a function $\operatorname {g} :B\rightarrow A$ with $\operatorname {g} \circ \operatorname {f} =\operatorname {id_{A}}$. Then $\forall x,x'\in A,\operatorname {f} (x)=\operatorname {f} (x')\Rightarrow \operatorname {g} (\operatorname {f} (x))=\operatorname {g} (\operatorname {f} (x'))\Rightarrow x=x'$. $\operatorname {f}$ is thus injective.
Q.E.D.

Definition: A function $\operatorname {f} :A\rightarrow B$ is surjective if

$\forall y\in B,\exists x\in A\mid \operatorname {f} (x)=y$

Lemma: Consider a function $\operatorname {f} :A\rightarrow B$. Then $\operatorname {f}$ is surjective if and only if there exists a function $\operatorname {g} :B\rightarrow A$ with $\operatorname {f} \circ \operatorname {g} =\operatorname {id_{B}}$.
Proof:
$'\Rightarrow '$:
Suppose $\operatorname {f}$ is surjective. We can define a suitable function $\operatorname {g} :B\rightarrow A$ as follows:

$\operatorname {g} (y):={\mbox{an }}x\in A\mid \operatorname {f} (x)=y$

It is now easy to verify that $\operatorname {f} \circ \operatorname {g} =\operatorname {id_{B}}$.
$'\Leftarrow '$:
Suppose there is a function $\operatorname {g} :B\rightarrow A$ with $\operatorname {f} \circ \operatorname {g} =\operatorname {id_{B}}$. Then $\forall y\in B{\mbox{, let }}x:=\operatorname {g} (y)$. Then $\operatorname {f} (x)=\operatorname {f} (\operatorname {g} (y))=y$. $\operatorname {f}$ is thus surjective.
Q.E.D.

Definition: A function $\operatorname {f} :A\rightarrow B$ is bijective if it is both injective and surjective.

Lemma: A function $\operatorname {f} :A\rightarrow B$ is bijective if and only if there exists a function $\operatorname {g} :B\rightarrow A$ with $\operatorname {g} \circ \operatorname {f} =\operatorname {id_{A}}$ and $\operatorname {f} \circ \operatorname {g} =\operatorname {id_{B}}$. Furthermore it can be shown that such a $\operatorname {g}$ is unique. We write it $\operatorname {f^{-1}} :B\rightarrow A$ and call it the inverse of $\operatorname {f}$.
Proof:
Left as an exercise.

Proposition: Consider a function $\operatorname {f} :A\rightarrow B$. Then

1. $f$ is injective iff $\forall S\subseteq A,f^{-1}(f(S))=S$
2. $f$ is surjective iff $\forall T\subseteq B,f(f^{-1}(T))=T$
3. $f$ is bijective iff the image and preimage of $f$ are inverse of each other

Example: If $A$ and $B$ are sets such that $B\subseteq A$, there exists an obviously injective function $i\,:\,B\rightarrow A$, called the inclusion $B\subseteq A$, such that $i(b)=b$ for all $b\in B$.

Example: If $\sim$ is an equivalence relation on a set $X$, there is an obviously surjective function $\pi \,:\,X\rightarrow X/\sim$, called the canonical projection onto $X/\sim$, such that $\pi (x)=[x]$ for all $x\in X$.

Theorem: Define the equivalence relation $\sim$ on $A$ such that $a\sim b$ if and only if $f(a)=f(b)$. Then, if $f:A\rightarrow B$ is any function, $f$ decomposes into the composition

$A{\stackrel {\pi }{\longrightarrow }}A/\sim {\stackrel {\tilde {f}}{\longrightarrow }}\mathrm {im} f{\stackrel {i}{\longrightarrow }}B$

where $\pi$ is the canonical projection, $i$ is the inclusion $\mathrm {im} \,f\subseteq B$, and ${\tilde {f}}$ is the bijection ${\tilde {f}}([a])=f(a)$ for all $a\in A$.

Proof: The definition of ${\tilde {f}}$ immediately implies that $f=i\circ {\tilde {f}}\circ \pi$, so we only have to prove that ${\tilde {f}}$ is well defined and a bijection. Let $a,a^{\prime }\in A$. Then $[a]=[a^{\prime }]\,\Rightarrow \,a\sim a^{\prime }\,\Rightarrow \,f(a)=f(a^{\prime })$. This shows that the value of ${\tilde {f}}([a])$ is independent of the representative chosen from $[a]$, and so it is well-defined.

For injectivity, we have ${\tilde {f}}([a])={\tilde {f}}([a^{\prime }])\,\Rightarrow \,f(a)=f(a^{\prime })\,\Rightarrow \,[a]=[a^{\prime }]$, so ${\tilde {f}}$ is injective.

For surjectivity, let $b\in \mathrm {im} \,f$. Then there exists an $a\in A$ such that $f(a)=b$, and so ${\tilde {f}}([a])=b$ by definition of ${\tilde {f}}$. Since $b$ is arbitrary in $\mathrm {im} \,f$, this proves that ${\tilde {f}}$ is surjective.

Q.E.D.

Definition: Given a function $f\,:\,X\rightarrow Y$, $f$ is a

(i) Monomorphism if given any two functions $g,h\,:\,W\rightarrow X$ such that $f\circ g=f\circ h$, then $g=h$.

(ii) Epimorphism if given any two functions $g,h\,:\,Y\rightarrow Z$ such that $g\circ f=h\circ f$, then $g=h$.

Theorem: A function between sets is

(i) a monomorphism if and only if it is injective.

(ii) an epimorphism if and only if it is surjective.

Proof: (i) Let $f\,:\,B\rightarrow C$ be a monomorphism. Then, for any two functions $g,h\,:\,A\rightarrow B$, $f(g(a))=f(h(a))\,\Rightarrow \,g(a)=h(a)$ for all $a\in A$. This is the definition if injectivity. For the converse, if $f$ is injective, it has a left inverse $f^{\prime }$. Thus, if $f(g(a))=f(h(a))$ for all $a\in A$, compose with $f^{\prime }$ on the left side to obtain $g(a)=h(a)$, such that $f$ is a monomorphism.

(ii) Let $f\,:\,A\rightarrow B$ be an epimorphism. Then, for any two functions $g,h\,:\,B\rightarrow C$, $g(f(a))=h(f(a))\,\Rightarrow \,g(b)=h(b)$ for all $a\in A$ and $b\in B$. Assume $\mathrm {im} f\neq B$, that is, that $f$ is not surjective. Then there exists at least one $b\in B$ not in $\mathrm {im} \,f$. For this $b$ choose two functions $g,h$ which coincide on $\mathrm {im} \,f$ but disagree on $\{b\}$. However, we still have $g(f(a))=h(f(a))$ for all $a\in A$. This violates our assumption that $f$ is an epimorphism. Consequentally, $f$ is surjective. For the converse, assume $f$ is surjective. Then the epimorphism property immediately follows.

Q.E.D.

Remark: The equivalence between monomorphism and injectivity, and between epimorphism and surjectivity is a special property of functions between sets. This not the case in general, and we will see examples of this when discussing structure-preserving functions between groups or rings in later sections.

Example: Given any two sets $A$ and $B$, we have the canonical projections $\pi _{A}\,:\,A\times B\rightarrow A$ sending $(a,b)$ to $a$, and $\pi _{B}\,:\,A\times B\rightarrow B$ sending $(a,b)$ to $b$. These maps are obviously surjective.

In addition, we have the natural inclusions $i_{A}\,:\,A\rightarrow A\coprod B$ and $i_{B}\,:\,B\rightarrow A\coprod B$ which are obviously injective as stated above.

Universal properties

The projections and inclusions described above are special, in that they satisfy what are called universal properties. We will give the theorem below. The proof is left to the reader.

Theorem: Let $A,B,C$ be any sets.

(i) Let $f\,:\,C\rightarrow A$ and $g\,:\,C\rightarrow B$. Then there exists a unique function $u\,:\,C\rightarrow A\times B$ such that $f=\pi _{A}\circ u$ and $g=\pi _{B}\circ u$ are simultaneously satisfied. $u$ is sometimes denoted $f\times g$.

(ii) Let $f\,:\,A\rightarrow C$ and $g\,:\,B\rightarrow C$. Then there exists a unique function $u\,:\,A\coprod B\rightarrow C$ such that $f=u\circ i_{A}$ and $g=u\circ i_{B}$ are simultaneously satifsied.

The canonical projections onto quotients also satisfy a universal property.

Theorem: Define the equivalence relation $\sim$ on $X$ and let $f\,:\,X\rightarrow Y$ be any function such that $a\sim b\,\Rightarrow \,f(a)=f(b)$ for all $a,b\in X$. Then there exists a unique function ${\bar {f}}\,:\,X/\sim \rightarrow Y$ such that $f={\bar {f}}\circ \pi$, where $\pi \,:\,X\rightarrow X/\sim$ is the canonical projection.

Binary Operations

A binary operation on a set $A$ is a function $*:A\times A\rightarrow A$. For $a,b\in A$, we usually write $*(a,b)$ as $a*b$.

Properties

The property that $a*b\in A$ for all $a,b\in A$ is called closure under $*$.

Example: Addition between two integers produces an integer result. Therefore addition is a binary operation on the integers. Whereas division of integers is an example of an operation that is not a binary operation. $1/2$ is not an integer, so the integers are not closed under division.

To indicate that a set $A$ has a binary operation $*$ defined on it, we can compactly write $(A,*)$. Such a pair of a set and a binary operation on that set is collectively called a binary structure. A binary structure may have several interesting properties. The main ones we will be interested in are outlined below.

Definition: A binary operation $*$ on $A$ is associative if for all $a,b,c\in A$, $(a*b)*c=a*(b*c)$.

Example: Addition of integers is associative: $(1+2)+3=6=1+(2+3)$. Notice however, that subtraction is not associative. Indeed, $2=1-(2-3)\neq (1-2)-3=-4$.

Definition: A binary operation $*$ on $A$ is commutative is for all $a,b\in A$, $a*b=b*a$.

Example: Multiplication of rational numbers is commutative: ${\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {ac}{bd}}={\frac {ca}{bd}}={\frac {c}{d}}\cdot {\frac {a}{b}}$. Notice that division is not commutative: $2\div 3={\frac {2}{3}}$ while $3\div 2={\frac {3}{2}}$. Notice also that commutativity of multiplication depends on the fact that multiplication of integers is commutative as well.

Exercise

• Of the four arithmetic operations, addition, subtraction, multiplication, and division, which are associative? commutative and identity?

Answer

operation	associative	commutative
Addition	yes	yes
Multiplication	yes	yes
Subtraction	No	No
Division	No	No

Algebraic structures

Binary operations are the working parts of algebraic structures:

Augustus De Morgan expressed the venture into the categories of algebraic structures as follows: It is "inventing a distinct system of unit-symbols, and investigating or assigning relations which define their mode of action on each other." De Morgan 1844, quoted by A.N. Whitehead, A Treatise on Universal Algebra, 1898, page 131.

One binary operation

A structure with one binary operation may be one of several types, depending on the conditions satisfied by the binary operation.

A closed binary operation o on a set A is called a magma (A, o ).

If the binary operation respects the associative law a o (b o c) = (a o b) o c, then the magma (A, o ) is a semigroup.

If a magma has an element e satisfying e o x = x = x o e for every x in it, then it is a unital magma. The element e is called the identity with respect to o. If a unital magma has elements x and y such that x o y = e, then x and y are inverses with respect to each other.

A magma for which every equation a x = b has a solution x, and every equation y c = d has a solution y, is a quasigroup. A unital quasigroup is a loop.

A unital semigroup is called a monoid. A monoid for which every element has an inverse is a group. A group for which x o y = y o x for all its elements x and y is called a commutative group. Alternatively, it is called an abelian group.

Two binary operations

A pair of structures, each with one operation, can used to build those with two: Take (A, o ) as a commutative group with identity e. Let A_ denote A with e removed, and suppose (A_ , * ) is a monoid with binary operation * that distributes over o:

a * (b o c) = (a * b) o (a * c). Then (A, o, * ) is a ring.

In this construction of rings, when the monoid (A_ , * ) is a group, then (A, o, * ) is a division ring or skew field. And when (A_ , * ) is a commutative group, then (A, o, * ) is a field.

The two operations sup (v) and inf (^) are presumed commutative and associative. In addition, the absorption property requires: a ^ (a v b) = a, and a v (a ^ b) = a. Then (A, v, ^ ) is called a lattice.

In a lattice, the modular identity is (a ^ b) v (x ^ b) = ((a ^ b) v x ) ^ b. A lattice satisfying the modular identity is a modular lattice.

Three binary operations

A module is a combination of a ring and a commutative group (A, B), together with a binary function A x B → B. When A is a field, then the module is a vector space. In that case A consists of scalars and B of vectors. The binary operation on B is termed addition.

Four binary operations

Suppose (A, B) is a vector space, and that B has a second operation called multiplication. Then the structure is an algebra over the field A.

Linear Algebra

The reader is expected to have some familiarity with linear algebra. For example, statements such as

Given vector spaces $V$ and $W$ with bases $B$ and $C$ and dimensions $n$ and $m$, respectively, a linear map $f\,:\,V\to W$ corresponds to a unique $m\times n$ matrix, dependent on the particular choice of basis.

should be familiar. It is impossible to give a summary of the relevant topics of linear algebra in one section, so the reader is advised to take a look at the linear algebra book.

In any case, the core of linear algebra is the study of linear functions, that is, functions with the property $f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)$, where greek letters are scalars and roman letters are vectors.

The core of the theory of finitely generated vector spaces is the following:

Every finite-dimensional vector space $V$ is isomorphic to $\mathbb {F} ^{n}$ for some field $\mathbb {F}$ and some $n\in \mathbb {N}$, called the dimension of $V$. Specifying such an isomorphism is equivalent to choosing a basis for $V$. Thus, any linear map between vector spaces $f\,:\,V\to W$ with dimensions $n$ and $m$ and given bases $\phi$ and $\psi$ induces a unique linear map $[f]_{\phi }^{\psi }\,:\,\mathbb {R} ^{n}\to \mathbb {R} ^{m}$. These maps are precisely the $m\times n$ matrices, and the matrix in question is called the matrix representation of $f$ relative to the bases $\phi ,\psi$.

Remark: The idea of identifying a basis of a vector space with an isomorphism to $\mathbb {F} ^{n}$ may be new to the reader, but the basic principle is the same. An alternative term for vector space is coordinate space since any point in the space may be expressed, on some particular basis, as a sequence of field elements. (All bases are equivalent under some non-singular linear transformation.) The name associated with pointy things like arrows, spears, or daggers, is distasteful to peace-loving people who don’t imagine taking up such a weapon. The orientation or direction associated with a point in coordinate space is implicit in the positive orientation of the real line (if that is the field) or in an orientation instituted in a polar expression of the multiplicative group of the field.

A coordinate space V with basis $\{e_{1},e_{2},...e_{n}\}$ has vectors $v=\sum _{i=1}^{n}x_{i}e_{i}=(x_{1},x_{2},...x_{n}).$ where e_i is all zeros except 1 at index i.

As an algebraic structure, V is an amalgam of an abelian group (addition and subtraction of vectors), a scalar field F (the source of the x_i's), its multiplicative group F *, and a group action F * x V → V, given by

$(k,v)\mapsto \sum _{i=1}^{n}kx_{i}e_{i}=(kx_{1},kx_{2},...kx_{n}).$ The group action is scalar-vector multiplication.

Linear transformations are mappings from one coordinate space V to another W corresponding to a matrix (a_{i j} ). Suppose W has basis

$\{f_{i}\}_{i=1}^{n}\ {\text{and vectors}}\ \ w=\sum _{i=1}^{n}y_{i}f_{i}=(y_{1},y_{2},...y_{n}).$

Then the elements of the matrix (a_{i j} ) are given by the rate of change of y_j depending on x_i:

$a_{ij}={\frac {\partial y_{j}}{\partial x_{i}}}=$ constant.

A common case involves V = W and n is a low number, such as n = 2. When F = {real numbers} = R, the set of matrices is denoted M(2,R). As an algebraic structure, M(2,R) has two binary operations that make it a ring: component-wise addition and matrix multiplication. See the chapter on 2x2 real matrices for a deconstruction of M(2,R) into a pencil of planar algebras.

More generally, when dim V = dim W = n, (a_{i j} ) is a square matrix, an element of M(n, F), which is a ring with the + and x binary operations. These benchmarks in algebra serve as representations. In particular, when the rows or columns of such a matrix are linearly independent, then there is a matrix (b_{i j} ) acting as a multiplicative inverse with respect to the identity matrix. The subset of invertible matrices is called the general linear group, GL(n, F). This group and its subgroups carry the burden of demonstrating physical symmetries associated with them.

The pioneers in this field included w:Sophus Lie, who viewed the continuous groups as evolving out of 1 in all directions according to an "algebra" now named after him. w:Hermann Weyl, spurred on by Eduard Study, explored and named GL(n, F) and its subgroups, calling them the classical groups.

Number Theory

As numbers of various number systems form basic units with which one must work when studying abstract algebra, we will now define the natural numbers and the rational integers as well as the basic operations of addition and multiplication. Using these definitions, we will also derive important properties of these number sets and operations. Following this, we will discuss important concepts in number theory; this will lead us to discussion of the properties of the integers modulo n.

The Peano postulates and the natural numbers

Definition: Using the undefined notions "1" and "successor" (denoted by $'$), we define the set of natural numbers without zero $\mathbb {N} ^{*}$, hereafter referred to simply as the natural numbers, with the following axioms, which we call the Peano postulates:

Axiom 1. $\exists 1(1\in \mathbb {N} ^{*}).$

Axiom 2. $\forall a(a\in \mathbb {N} ^{*}\implies \exists b(b=a')).$

Axiom 3. $\lnot \exists a(a'=1).$

Axiom 4. $\forall a\in \mathbb {N} ^{*}(\forall b\in \mathbb {N} ^{*}(a'=b'\implies a=b)).$

Axiom 5. $\forall A\subseteq \mathbb {N} ^{*}((1\in A)\land \forall a\in A(a'\in A)\implies A=\mathbb {N} ^{*}).$

We can prove theorems for natural numbers using mathematical induction as a consequence of the fifth Peano Postulate.

Addition

Definition: We recursively define addition for the natural numbers as a composition using two more axioms; the other properties of addition can subsequently be derived from these axioms. We denote addition with the infix operator +.

Axiom 6. $\forall a\in \mathbb {N} ^{*}(a+1=a').$

Axiom 7. $\forall a\in \mathbb {N} ^{*}(\forall b\in \mathbb {N} ^{*}(a+b'=(a+b)')).$

Axiom 6 above relies on the first Peano postulate (for the existence of 1) as well as the second (for the existence of a successor for every number).

Henceforth, we will assume that proven theorems hold for all $a,b,c,\ldots ,n$ in $\mathbb {N} ^{*}$.

Multiplication

Definition: We similarly define multiplication for the natural numbers recursively, again using two axioms:

Axiom 8. $a(1)=a.$

Axiom 9. $ab'=ab+a.$

Properties of addition

We start by proving that addition is associative.

Theorem 1: Associativity of addition: $(a+b)+c=a+(b+c).$

Proof: Base case: By axioms 6 and 7, $a+(b+1)=(a+b)'$.

By axiom 6, $a+(b+1)=(a+b)+1$.

Inductive hypothesis: Suppose that, for $k'>1$, $(a+b)+k=a+(b+k)$.

Inductive step: By axiom 7, $(a+b)+k'=\left[(a+b)+k\right]'$.

By the inductive hypothesis, $(a+b)+k'=\left[a+(b+k)\right]'$.

By axiom 7, $(a+b)+k'=a+(b+k)'$.

By axiom 7, $(a+b)+k'=a+(b+k')$.

By induction, $(a+b)+c=a+(b+c)$. QED.

Lemma 1: $a+1=1+a.$

Proof: Base case: 1+1=1+1.

Inductive hypothesis: Suppose that, for $k'>1$, $k+1=1+k$.

Inductive step: By axiom 6, $k'+1=(k+1)+1$.

By the inductive hypothesis, $k'+1=(1+k)+1$.

By theorem 1, $k'+1=1+(k+1)$.

By axiom 6, $k'+1=1+k'$.

By induction, $a+1=1+a$. QED.

Theorem 2: Commutativity of addition: $a+b=b+a.$

Proof: Base case: By lemma 1, $a+1=1+a$.

Inductive hypothesis: Suppose that, for $k'>1$, $a+k=k+a$.

By axiom 6, $a+k'=a+(k+1)$.

By theorem 1, $a+k'=(a+k)+1$.

By the inductive hypothesis, $a+k'=(k+a)+1$.

By theorem 1, $a+k'=k+(a+1)$.

By lemma 1, $a+k'=k+(1+a)$.

By theorem 1, $a+k'=(k+1)+a$.

By axiom 6, $a+k'=k'+a$.

By induction, $a+b=b+a$. QED.

Theorem 3: $a+b=a+c\implies b=c$.

Proof: Base case: Suppose $1+b=1+c$.

By theorem 2, $b+1=c+1$.

By axiom 6, $b'=c'$.

By axiom 4, $b=c$.

Inductive hypothesis: Suppose that, for $k'>1$, $k+b=k+c\implies b=c$.

Inductive step: Suppose $k'+b=k'+c$.

By axiom 6, $(k+1)+b=(k+1)+c$.

By theorem 2, $(1+k)+b=(1+k)+c$.

By theorem 1, $1+(k+b)=1+(k+c)$.

By the base case, $k+b=k+c$. Thus, $k'+b=k'+c\implies k+b=k+c$.

By the inductive hypothesis, $k'+b=k'+c\implies b=c$.

By induction, $a+b=a+c\implies b=c$. QED.

Properties of multiplication

Theorem 4: Left-distributivity of multiplication over addition: $a(b+c)=ab+ac$.

Proof: Base case: By axioms 6 and 9, $a(b+1)=ab+a$.

By axiom 8, $a(b+1)=ab+a(1)$.

Inductive hypothesis: Suppose that, for $k'>1$, $a(b+k)=ab+ak$.

Inductive step: By axiom 7, $a(b+k')=a(b+k)'$.

By axiom 9, $a(b+k')=a(b+k)+a$.

By the inductive hypothesis, $a(b+k')=(ab+ak)+a$.

By theorem 1, $a(b+k')=ab+(ak+a)$.

By axiom 9, $a(b+k')=ab+ak'$.

By induction, $a(b+c)=ab+ac$. QED.

Theorem 5: $1a=a$.

Proof: Base case: By axiom 8, 1(1)=1.

Inductive hypothesis: Suppose that, for $k'>1$, $1k=k$.

Inductive step: By axiom 6, $1k'=1(k+1)$.

By theorem 4, $1k'=1k+1(1)$.

By the base case, $1k'=1k+1$.

By the inductive hypothesis, $1k'=k+1$.

By axiom 6, $1k'=k'$.

By induction, $1a=a$. QED.

Theorem 6: $a'b=ab+b$.

Proof: Base case: By axiom 8, $a'(1)=a'$.

By axiom 6, $a'(1)=a+1$.

By axiom 8, $a'(1)=a(1)+1$.

Inductive hypothesis: Suppose that, $k'>1$, $a'k=ak+k$.

Inductive step: By axiom 9, $a'k'=a'k+a'$.

By the inductive hypothesis, $a'k'=ak+k+a'$.

By axiom 6, $a'k'=ak+k+(a+1)$.

By theorem 1, $a'k'=ak+(k+a)+1$.

By theorem 2, $a'k'=ak+(a+k)+1$.

By theorem 1, $a'k'=ak+a+k+1$

By axiom 9, $a'k'=ak'+k+1$.

By theorem 1, $a'k'=ak'+(k+1)$.

By axiom 6, $a'k'=ak'+k'$.

By induction, $a'b=ab+b$. QED.

Theorem 7: Associativity of multiplication: $(ab)c=a(bc).$

Proof: Base case: By axiom 8, $ab(1)=ab=a\left[b(1)\right]$.

Inductive hypothesis: Suppose that, for $k'>1$, $(ab)k=a(bk)$.

Inductive step: By axiom 9, $(ab)k'=(ab)k+ab$.

By the inductive hypothesis, $(ab)k'=a(bk)+ab$.

By theorem 4, $(ab)k'=a(bk+b)$.

By axiom 9, $(ab)k'=a(bk')$.

By induction, $(ab)c=a(bc)$. QED.

Theorem 8: Commutativity of multiplication: $ab=ba$.

Proof: Base case: By axiom 8 and theorem 5, $a(1)=a=1a$.

Inductive hypothesis: Suppose that, for $k'>1$, $ak=ka$.

Inductive step: By axiom 9, $ak'=ak+a$.

By the inductive hypothesis, $ak'=ka+a$.

By theorem 6, $ak'=k'a$.

By induction, $ab=ba$. QED.

Theorem 9: Right-distributivity of multiplication over addition: $(a+b)c=ac+bc$.

Proof: By theorems 4 and 7, $(a+b)c=ca+cb$.

By theorem 7, $(a+b)c=ac+bc$. QED.

The integers

The set of integers $\mathbb {Z}$ can be constructed from ordered pairs of natural numbers (a, b). We define an equivalence relation on the set of all such ordered pairs such that

$(a,b)\equiv (c,d)\Leftrightarrow a+d=c+b.$

Then the set of rational integers is the set of all equivalence classes of such ordered pairs. We will denote the equivalence class of which some pair (a, b) is a member with the notation [(a, b)]. Then, for any natural numbers a and b, [(a, b)] represents a rational integer.

Integer addition

Definition: We define addition for the integers as follows:

$\left[(a,b)\right]+\left[(c,d)\right]=\left[(a+c,b+d)\right].$

Using this definition and the properties for the natural numbers, one can prove that integer addition is both associative and commutative.

Integer multiplication

Definition: Multiplication for the integers, like addition, can be defined with a single axiom:

$\left[(a,b)\right]\left[(c,d)\right]=\left[(ac+bd,ad+bc)\right].$

Again, using this definition and the previously-proven properties of natural numbers, it can be shown that integer multiplication is commutative and associative, and furthermore that it is both left- and right-distributive with respect to integer addition.

Group Theory/Group

In this section we will begin to make use of the definitions we made in the section about binary operations. In the next few sections, we will study a specific type of binary structure called a group. First, however, we need some preliminary work involving a less restrictive type of binary structure.

Monoids

Definition 1: A monoid is a binary structure $(M,*)$ satisfying the following properties:

(i) $(a*b)*c=a*(b*c)$ for all $a,b,c\in M$. This is defined as associativity.

(ii) There exists an identity element $e\in M$ such that $a*e=a=e*a$ for all $a\in M$.

Now we have our axioms in place, we are faced with a pressing question; what is our first theorem going to be? Since the first few theorems are not dependent on one another, we simply have to make an arbitrary choice. We choose the following:

Theorem 2: The identity element of $M$ is unique.

Proof: Assume $e$ and $e^{\prime }$ are both identity elements of $M$. Then both satisfy condition (ii) in the definition above. In particular, $e=e*e^{\prime }=e^{\prime }$, proving the theorem. ∎

This theorem will turn out to be of fundamental importance later when we define groups.

Theorem 3: If $a_{1},a_{2},\ldots ,a_{n}$ are elements of $M$ for some $n\in \mathbb {N}$, then the product $a_{1}*a_{2}*\cdots *a_{n}$ is unambiguous.

Proof: We can prove this by induction. The cases for $n=1$ and $n=2$ are trivially true. Assume that the statement is true for all $n<k$. For $n=k$, the product $a_{1}*\cdots *a_{k}$, inserting parentheses, can be "partitioned" into $(a_{1}*\cdots *a_{i})*(a_{i+1}*\cdots *a_{k})$. Both parts of the product have a number of elements less than $k$ and are thus unambiguous. The same is true if we consider a different "partition", $(a_{1}*\cdots *a_{j})*(a_{j+1}*\cdots *a_{k})$, where $j>i$. Thus, we can unambiguously compute the products $(a_{1}*\cdots *a_{i})$, $(a_{i+1}*\cdots *a_{j})$, and $(a_{j+1}*\cdots *a_{k})$, and rewrite the two "partitions" as $b_{1}*(b_{2}*b_{3})$ and $(b_{1}*b_{2})*b_{3}$. These equal each other by the definition of a monoid.∎

This is about as far as we are going to take the idea of a monoid. We now proceed to groups.

Groups

Definition 4: A group is a monoid $(G,*)$ that also satisfies the property

(iii) For each $a\in G$, there exists an element $a^{\prime }\in G$ such that $a*a^{\prime }=a^{\prime }*a=e$.

Such an element $a^{\prime }$ is called an inverse of $a$. When the operation on the group is understood, we will conveniently refer to $(G,*)$ as $G$. In addition, we will gradually stop using the symbol $*$ for multiplication when we are dealing with only one group, or when it is understood which operation is meant, instead writing products by juxtaposition, $a*b\equiv ab$.

Remark 5: Notice how this definition depends on Theorem 2 to be well defined. Therefore, we could not state this definition before at least proving uniqueness of the identity element. Alternatively, we could have included the existence of a distinguished identity element in the definition. In the end, the two approaches are logically equivalent.

Also note that to show that a monoid is a group, it is sufficient to show that each element has either a left-inverse or a right-inverse. Let $a\in G$, let $b$ be a right-inverse of $a$, and let $c$ be a right-inverse of $b$. Then, $a=a(bc)=(ab)c=c$. Thus, any right-inverse is also a left-inverse, or $ab=ba$. A similar argument can be made for left-inverses.

Theorem 6: The inverse of any element is unique.

Proof: Let $g\in G$ and let $g^{\prime }$ and $g^{\prime \prime }$ be inverses of $g$. Then, $g^{\prime }=g^{\prime }*e=g^{\prime }*g*g^{\prime \prime }=e*g^{\prime \prime }=g^{\prime \prime }$. ∎

Thus, we can speak of the inverse of an element, and we will denote this element by $a^{-1}$. We also observe this nice property:

Corollary 7: $(a^{-1})^{-1}=a$.

Proof: This follows immediately since $a*a^{-1}=a^{-1}*a=e$.

The next couple of theorems may appear obvious, but in the interest of keeping matters fairly rigorous, we allow ourselves to state and prove seemingly trivial statements.

Theorem 8: Let $G$ be a group and $a,b\in G$. Then $(a*b)^{-1}=b^{-1}*a^{-1}$.

Proof: The result follows by direct computation: $(a*b)*(b^{-1}*a^{-1})=a*b*b^{-1}*a^{-1}=a*e*a^{-1}=a*a^{-1}=e$. ∎

Theorem 9: Let $a,b,c\in G$. Then, $a*b=a*c$ if and only if $b=c$. Also, $a*c=b*c$ if and only if $a=b$.

Proof: We will prove the first assertion. The second is identical. Assume $a*b=a*c$. Then, multiply on the left by $a^{-1}$ to obtain $b=c$. Secondly, assume $b=c$. Then, multiply on the left by $a$ to obtain $a*b=a*c$. ∎

Theorem 10: The equation $a*x=b$ has a unique solution in $G$ for any $a,b\in G$.

Proof: We must show existence and uniqueness. For existence, observe that $x=a^{-1}*b$ is a solution in $G$. For uniqueness, multiply both sides of the equation on the left by $a^{-1}$ to show that this is the only solution. ∎

Notation: Let $G$ be a group and $a\in G$. We will often encounter a situation where we have a product $\underbrace {a*a*\cdots *a} _{\mathrm {n\,terms} }$. For these situations, we introduce the shorthand notation $a^{n}=\underbrace {a*a*\cdots *a} _{\mathrm {n\,terms} }$ if $n$ is positive, and $a^{n}=\underbrace {a^{-1}*a^{-1}*\cdots *a^{-1}} _{\mathrm {|n|\,terms} }$ if $n$ is negative. Under these rules, it is straightforward to show $g^{n}*g^{m}=g^{n+m}$ and $(a^{n})^{-1}=a^{-n}$ and $a^{0}=e$ for all $a\in G$.

Definition 11: (i) The order of a group $G$, denoted $|G|$ or $o(G)$, is the number of elements of $G$ if $G$ is finite. Otherwise $|G|$ is said to be infinite.

(ii) The order of an element of $g\in G$, similarly denoted $|g|$ or $o(g)$, is defined as the lowest positive integer $n$ such that $g^{n}=e$ if such an integer exists. Otherwise $|g|$ is said to be infinite.

Theorem 12: Let $G$ be a group and $a,b\in G$. Then $|ab|=|ba|$.

Proof: Let the order of $ab$ be $n$. Then, $(ab)^{n}=abab...ab=e$, $n$ being the smallest positive integer such that this is true. Now, multiply by $b$ on the left and $a$ on the right to obtain $(ba)^{n+1}=ba$ implying $(ba)^{n}=e$. Thus, we have shown that $|ba|\leq |ab|$. A similar argument in the other direction shows that $|ab|\leq |ba|$. Thus, we must have $|ab|=|ba|$, proving the theorem. ∎

Corollary 13: Let $G$ be a group with $a,b\in G$. Then, $|aba^{-1}|=|b|$.

Proof: By Theorem 12, we have that $|aba^{-1}|=|ba^{-1}a|=|be|=|b|$. ∎

Theorem 14: An element of a group not equal to the identity has order 2 if and only if it is its own inverse.

Proof: Let $g$ have order 2 in the group $G$. Then, $g^{2}=gg=e$, so by definition, $g^{-1}=g$. Now, assume $g^{-1}=g$ and $g\neq e$. Then $e=gg^{-1}=gg=g^{2}$. Since $g\neq e$, 2 is the smallest positive integer satisfying this property, so $g$ has order 2. ∎

Definition 15: Let $G$ be a group such that for all $a,b\in G$, $ab=ba$. Then, $G$ is said to be commutative or abelian.

When we are dealing with an abelian group, we will sometimes use so-called additive notation, writing $+$ for our binary operation and replacing $a^{n}$ with $na$. In such cases, we only need to keep track of the fact that $n$ is an integer while $a$ is a group element. We will also talk about the sum of elements rather than their product.

Abelian groups are in many ways nicer objects than general groups. They also admit more structure where ordinary groups do not. We will see more about this later when we talk about structure-preserving maps between groups.

Definition 16: Let $G$ be a group. A subset $S\subseteq G$ is called a generating set for $G$ if every element in $G$ can be written in terms of elements in $S$. We write $G=\langle S\rangle =\{s_{1}^{e_{1}}\ldots s_{m}^{e_{m}}\mid s_{i}\in S,e_{i}\in \{1,-1\}\}$.

Now that we have our definitions in place and have a small arsenal of theorems, let us look at three (really, two and a half) important families of groups.

Multiplication tables

We will now show a convenient way of representing a group structure, or more precisely, the multiplication rule on a set. This notion will not be limited to groups only, but can be used for any structure with any number of operations. As an example, we give the group multiplication table for the Klein 4-group $K_{4}$. The multiplication table is structured such that $g*h$ is represented by the element in the "$(g,h)$-position", that is, in the intersection of the $g$-row and the $h$-column.

${\begin{array}{c|cccc}*&e&a&b&c\\\hline e&e&a&b&c\\a&a&e&c&b\\b&b&c&e&a\\c&c&b&a&e\end{array}}$

This next group is for the group of integers under addition modulo 4, called $\mathbb {Z} _{4}$. We will learn more about this group later.

${\begin{array}{c|cccc}+&0&1&2&3\\\hline 0&0&1&2&3\\1&1&2&3&0\\2&2&3&0&1\\3&3&0&1&2\end{array}}$

We can clearly see that $K_{4}$ and $\mathbb {Z} _{4}$ are "different" groups. There is no way to relabel the elements such that the multiplication tables coincide. There is a notion of "equality" of groups that we have not yet made precise. We will get back to this in the section about group homomorphisms.

The reader might have noticed that each row in the group table features each element of the group exactly once. Indeed, assume that an element $k\in G$ appeared twice in some row of the multiplication table for $G$. Then there would exist $g,h,h^{\prime }\in G$ such that $gh=gh^{\prime }$, implying $h=h^{\prime }$ and contradicting the assumption of $k$ appearing twice. We state this as a theorem:

Theorem 17: Let $G$ be a group and $a\in G$. Then $aG=\{a*g\mid g\in G\}=G$.

Using this, the reader can use a multiplication table to find all groups of order 3. He/she will find that there is only one possibility.

Problems

Problem 1: Show that $M_{n}(\mathbb {R} )$, the set of $n\times n$ matrices with real entries, forms a group under the operation of matrix addition.

Problem 2: Let $V,W$ be vector spaces and $\mathrm {Hom} (V,W)$ be the set of linear maps from $V$ to $W$. Show that $\mathrm {Hom} (V,W)$ forms an abelian group by defining $(f+g)(v)=f(v)+g(v)$.

Problem 3: Let $\mathbb {Q} _{8}$ be generated by the elements $i,j,k,m$ such that $i^{2}=j^{2}=k^{2}=m$, $m^{2}=e$ and $ij=mji=k$. Show that $\mathbb {Q} _{8}$ forms a group. Are any of the conditions above redundant? When the identity e is written 1 and m = −1, then $\mathbb {Q} _{8}$ is called the quaternion group. The $i,\ j,\ k$ are imaginary units. Using 1 and one of these as a basis for a number plane results in the complex number plane.

Problem 4: Let $S$ be any nonempty set and consider the set $G^{S}$. Show that $G^{S}$ has a natural group structure.

Answer

$G^{S}$ is the set of functions $f\,:\,S\rightarrow G$. Let $f_{1},f_{2}\in G^{S}$ and define the binary operation $(f_{1}*f_{2})(x)=f_{1}(x)f_{2}(x)$ for all $x\in S$. Then $G^{S}$ is a group with identity $0$ such that $0(x)=e$ for all $x\in X$ and inverses $f^{-1}(x)=f(x)^{-1}$ for all $f\in G^{S},x\in X$.∎

Problem 5: Let $G$ be a group with two distinct elements $a$ and $b$, both of order 2. Show that $G$ has a third element of order 2.

Answer

We consider first the case where $ab=ba$. Then $(ab)^{2}=abab=aabb=e$ and $ab$ is distinct from $e,a$ and $b$. If $ab\neq ba$, then $(aba^{-1})^{2}=abaa^{-1}ba^{-1}=abba^{-1}=e$ and $aba^{-1}$ is distinct from $e,a$ and $b$. ∎

Problem 6: Let $G$ be a group with one and only one element $f$ of order 2. Show that $\prod _{g\in G}g=f$.

Answer

Since the product of two elements generally depends on the order in which we multiply them, the stated product is not necessarily well-defined. However, it works out in this case.

Since every element of $G$ appears once in the product, for every element $g\in G$, the inverse of $g$ must appear somewhere in the product. That, is, unless $|g|=2$ in which case $g$ is its own inverse by Theorem 14. Now, applying Corollary 13 to the product shows that its order is that same as the order of the product of all elements of order 2 in $G$. But there is only one such element, $f$, so the order of the product is 2. Since the only element in $G$ having order 2 is $f$, the equality follows. ∎

Group Theory/Subgroup

Subgroups

We are about to witness a universal aspect of mathematics. That is, whenever we have any sort of structure, we ask ourselves: does it admit substructures? In the case of groups, the answer is yes, as we will immediately see.

Definition 1: Let $G$ be a group. Then, if $H\subseteq G$ is a subset of $G$ which is a group in its own right under the same operation as $G$, we call $H$ a subgroup of $G$ and write $H\leq G$.

Example 2: Any group $G$ has at least 2 subgroups; $G$ itself and the trivial group $\{e\}$. These are called the improper and trivial subgroups of $G$, respectively.

Naturally, we would like to have a method of determining whether a given subset of a group is a subgroup. The following two theorems provide this. Since $H$ naturally inherits the associativity property from $G$, we only need to check closure.

Theorem 3: A nonempty subset $H$ of a group $G$ is a subgroup if and only if

(i) $H$ is closed under the operation on $G$. That is, if $a,b\in H$, then $ab\in H$,

(ii) $e\in H$,

(iii) $H$ is closed under the taking of inverses. That is, if $a\in H$, then $a^{-1}\in H$.

Proof: The left implication follows directly from the group axioms and the definition of subgroup. For the right implication, we have to verify each group axiom for $H$. Firstly, since $H$ is closed, it is a binary structure, as required, and as mentioned, $H$ inherits associativity from G. In addition, $H$ has the identity element and inverses, so $H$ is a group, and we are done. ∎

There is, however, a more effective method. Each of the three criteria listed above can be condensed into a single one.

Theorem 4: Let $G$ be a group. Then a nonempty subset $H\subseteq G$ is a subgroup if and only if $a,b\in H\,\Rightarrow \,ab^{-1}\in H$.

Proof: Again, the left implication is immediate. For the right implication, we have to verify the (i)-(iii) in the previous theorem. First, assume $a\in H$. Then, letting $b=a$, we obtain $aa^{-1}=e\in H$, taking care of (ii). Now, since $e,a\in H$ we have $ea^{-1}=a^{-1}\in H$ so $H$ is closed under taking of inverses, satisfying (iii). Lastly, assume $a,b\in H$. Then, since $b^{-1}\in H$, we obtain $a(b^{-1})^{-1}=ab\in H$, so $H$ is closed under the operation of $G$, satisfying (i), and we are done. ∎

All right, so now we know how to recognize a subgroup when we are presented with one. Let's take a look at how to find subgroups of a given group. The next theorem essentially solves this problem.

Theorem 5: Let $G$ be a group and $g\in G$. Then the subset $\{g^{n}\mid n\in \mathbb {Z} \}$ is a subgroup of $G$, denoted $\langle g\rangle$ and called the subgroup generated by $g$. In addition, this is the smallest subgroup containing $g$ in the sense that if $H$ is a subgroup and $g\in H$, then $\langle g\rangle \leq H$.

Proof: First we prove that $\langle g\rangle$ is a subgroup. To see this, note that if $h,k\in \langle g\rangle$, then there exists integers $n,m\in \mathbb {Z}$ such that $h=g^{n}\,,\,k=g^{m}$. Then, we observe that $hk^{-1}=g^{n}g^{-m}=g^{n-m}\in \langle g\rangle$ since $n-m\in \mathbb {Z}$, so $\langle g\rangle$ is a subgroup of $G$, as claimed. To show that it is the smallest subgroup containing $g$, observe that if $H$ is a subgroup containing $g$, then by closure under products and inverses, $g^{n}\in H$ for all $n\in Z$. In other words, $\langle g\rangle \subseteq H$. Then automatically $\langle g\rangle \leq H$ since $\langle g\rangle$ is a subgroup of $G$. ∎

Theorem 6: Let $H$ and $H^{\prime }$ be subgroups of a group $G$. Then $H\cap H^{\prime }$ is also a subgroup of $G$.

Proof: Since both $H$ and $H^{\prime }$ contain the identity element, their intersection is nonempty. Let $a,b\in H\cap H^{\prime }$. Then $a,b\in H$ and $a,b\in H^{\prime }$. Since both $H$ and $H^{\prime }$ are subgroups, we have $ab^{-1}\in H$ and $ab^{-1}\in H^{\prime }$. But then $ab^{-1}\in H\cap H^{\prime }$. Thus $H\cap H^{\prime }$ is a subgroup of $G$. ∎

Theorem 6 can easily be generalized to apply for any arbitrary intersection $\bigcap _{i\in I}H_{i}$ where $H_{i}$ is a subgroup for every $i$ in an arbitrary index set $I$. The reasoning is identical, and the proof of this generalization is left to the reader to formalize.

Definition 7: Let $G$ be a group and $H$ be a subgroup of $G$. Then $gH=\{gh\mid h\in H\}$ is called a left coset of $H$. The set of all left cosets of $H$ in $G$ is denoted $G/H$. Likewise, $Hg=\{hg\mid h\in H\}$ is called a right coset, and the set of all right cosets of $H$ in $G$ is denoted $H\backslash G$.

Lemma 8: Let $G$ be a group and $H$ be a subgroup of $G$. Then every left coset has the same number of elements.

Proof: Let $g\in G$ and define the function $f\,:\,H\rightarrow gH$ by $h\mapsto gh$. We show that $f$ is a bijection. Firstly, $gh=gh^{\prime }\,\Rightarrow \,h=h^{\prime }$ by left cancellation, so $f$ is injective. Secondly, let $h^{\prime }\in gH$. Then $h^{\prime }=gh$ for some $h\in H$ and $f(h)=h^{\prime }$, so $f$ is surjective and a bijection. It follows that $|H|=|gH|$, as was to be shown. ∎

Lemma 9: The relation $\sim$ defined by $a\sim b\,\Leftrightarrow \,a^{-1}b\in H$ is an equivalence relation.

Proof: Reflexivity and symmetry are immediate. For transitivity, let $a\sim b$ and $b\sim c$. Then $a^{-1}b,b^{-1}c\in H$, so $a^{-1}c\in H$ and we are done. ∎

Lemma 10: Let $G$ be a group and $H$ be a subgroup of $G$. Then the left cosets of $H$ partition $G$.

Proof: Note that $aH=bH\Leftrightarrow ah=bh^{\prime }\,\Leftrightarrow a^{-1}bh^{\prime }=h\,\Leftrightarrow a^{-1}b\in H$ for some $h,h^{\prime }\in H$. Since $a\sim b\,\Leftrightarrow \,a^{-1}b\in H$ is an equivalence relation and the equivalence classes are the left cosets of $H$, these automatically partition $G$. ∎

Theorem 11 (Lagrange's theorem): Let $G$ be a finite group and $H$ be a subgroup of $G$. Then $|G|=|G/H||H|$.

Proof: By the previous lemmas, each left coset has the same number of elements $|H|$ and every $g\in G$ is included in a unique left coset $gH$. In other words, $G$ is partitioned by $|G/H|$ left cosets, each contributing an equal number of elements $|H|$. The theorem follows. ∎

Note 12: Each of the previous theorems have analagous versions for right cosets, the proofs of which use identical reasoning. Stating these theorems and writing out their proofs are left as an exercise to the reader.

Corollary 13: Let $G$ be a group and $H$ be a subgroup of $G$. Then right and left cosets of $H$ have the same number of elements.

Proof: Since $H$ is a left and a right coset we immediately have $|gH|=|H|=|Hg^{\prime }|$ for all $g,g^{\prime }\in G$. ∎

Corollary 14: Let $G$ be a group and $H$ be a subgroup of $G$. Then the number of left cosets of $H$ in $G$ and the number of right cosets of $H$ in $G$ are equal.

Proof: By Lagrange's theorem and its right coset counterpart, we have $|H||H\backslash G|=|G|=|G/H||H|$. We immediately obtain $|H\backslash G|=|G/H|$, as was to be shown. ∎

Now that we have developed a reasonable body of theory, let us look at our first important family of groups, namely the cyclic groups.

Problems

Problem 1 (Matrix groups): Show that:

i) The group $GL(n,\mathbb {R} )=\{A\in M_{n}(\mathbb {R} )\mid \det(A)\neq 0\}$ of invertible $n\times n$ matrices is a subgroup of $M_{n}(\mathbb {R} )$. This group is called the general linear group of order $n$.

ii) The group $O(n)=\{A\in M_{n}(\mathbb {R} )\mid AA^{T}=I\}$ of $n\times n$ orthogonal matrices is a subgroup of $GL(N,\mathbb {R} )$. This group is called the orthogonal group of order $n$.

iii) The group $SO(n)=\{A\in M_{n}(\mathbb {R} )\mid AA^{T}=I\,\wedge \,\det(A)=1\}$ is a subgroup of $O(n)$. This group is called the special orthogonal group of roder $n$.

iv) The group $U(n)=\{A\in M_{n}(\mathbb {C} )\mid AA^{*}=I\}$ of unitary matrices is a subgroup of $GL(n,\mathbb {C} )$. This is called the unitary group of order $n$.

v) The group $SU(n)=\{A\in M_{n}(\mathbb {C} )\mid AA^{*}=I\,\wedge \,\det(A)=1\}$ is a subgroup of $U(n)$. This is called the special unitary group of order $n$.

Problem 2: Show that if $H,K$ are subgroups of $G$, then $H\cup K$ is a subgroup of $G$ if and only if $H\subseteq K$ or $K\subseteq H$.

• Definition of a Subgroup

• Subgroup Inherits Identity
• Intersection of Subgroups is a Subgroup

• Definition of a Coset

• a Subgroup and its Cosets have Equal Orders
• a Group is Partitioned by Cosets of Its Subgroup

• Lagrange's Theorem

• Definition of a Cyclic Subgroup

• Order of a Cyclic Subgroup Help!
• Euler's Totient Theorem

• Definition of a Normal Subgroup

Group Theory/Cyclic groups

• A cyclic group generated by g is

• $\langle g\rangle =\lbrace g^{n}\;|\;n\in \mathbb {Z} \rbrace$

• where $g^{n}={\begin{cases}\underbrace {g\ast g\cdots \ast g} _{n},&n\in \mathbb {Z} ,n\geq 0\\\underbrace {g^{-1}\ast g^{-1}\cdots \ast g^{-1}} _{-n},&n\in \mathbb {Z} ,n<0\end{cases}}$

• Induction shows: $g^{m+n}=g^{m}\ast g^{n}{\text{ and }}g^{mn}=[g^{m}]^{n}$

Theorem

Let C_m be a cyclic group of order m generated by g with $\ast$

Let $(\mathbb {Z} /m,+)$ be the group of integers modulo m with addition

C_m is isomorphic to $(\mathbb {Z} /m,+)$

Lemma

Let n be the minimal positive integer such that gⁿ = e

$g^{i}=g^{j}\leftrightarrow i=j~{\text{mod}}~n$

Proof of Lemma

Let i > j. Let i - j = sn + r where 0 ≤ r < n and s,r,n are all integers.

1. $g^{i}=g^{j}\;$
2. $e=g^{i-j}=g^{sn+r}=[g^{n}]^{s}\ast g^{r}=[e]^{s}\ast g^{r}=g^{r}$	as i - j = sn + r, and gn = e
3. $g^{r}=e$
4. $r=0$	as n is the minimal positive integer such that gn = e and 0 ≤ r < n
5. $i-j=sn$	0. and 7.
6. $i=j~{\text{mod}}~n$

Proof

0. Define   ${\begin{aligned}f\colon C_{m}&\to \mathbb {Z} /m\\g^{i}&\mapsto i~{\text{mod}}~m\end{aligned}}$

Lemma shows f is well defined (only has one output for each input).

f is homomorphism:

$f(g^{i})+f(g^{j})=i+j~{\text{mod}}~m=f(g^{i+j})=f(g^{i}\ast g^{j})$

f is injective by lemma

f is surjective as both $\mathbb {Z} /m$ and $C_{m}$ have m elements and f is injective

Cyclic groups

In the previous section about subgroups we saw that if $G$ is a group with $g\in G$, then the set of powers of $g$, $\langle g\rangle =\{g^{n}\mid n\in \mathbb {Z} \}$ constituted a subgroup of $G$, called the cyclic subgroup generated by $g$. In this section, we will generalize this concept, and in the process, obtain an important family of groups which is very rich in structure.

Definition 1: Let $G$ be a group with an element $g\in G$ such that $\langle g\rangle =G$. Then $G$ is called a cyclic group, and $g$ is called a generator of $G$. Alternatively, $g$ is said to generate $G$. If there exists an integer $n$ such that $g^{n}=e$, and $n$ is the smallest positive such integer, $G$ is denoted $C_{n}$, the cyclic group of order $n$. If no such integer exists, $G$ is denoted $C_{\infty }$, the infinite cyclic group.

The infinite cyclic group can also be denoted $F_{\{g\}}$, the free group with one generator. This is foreshadowing for a future section and can be ignored for now.

Theorem 2: Any cyclic group is abelian.

Proof: Let $G$ be a cyclic group with generator $g$. Then if $h,k\in G$, then $h=g^{n}$ and $k=g^{m}$ for some $n,m\in \mathbb {Z}$. To show commutativity, observe that $hk=g^{n}g^{m}=g^{n+m}=g^{m+n}=g^{m}g^{n}=kh$ and we are done. ∎

Theorem 3: Any subgroup of a cyclic group is cyclic.

Proof: Let $G$ be a cyclic group with generator $g$, and let $H\leq G$. Since $G=\langle g\rangle$, in particular every element of $H$ equals $g^{n}$ for some $n\in \mathbb {Z}$. We claim that if $a$ the lowest positive integer such that $g^{a}\in H$, then $H=\langle g^{a}\rangle$. To see this, let $g^{n}\in H$. Then $n=qa+r$ and $0\leq r<a$ for unique $q,r\in \mathbb {Z}$. Since $H$ is a subgroup and $g^{a}\in H$, we must have $g^{n}(g^{a})^{-q}=g^{qa+r}g^{-qa}=g^{r}\in H$. Now, assume that $r>0$. Then $g^{r}\in H$ contradicts our assumption that $a$ is the least positive integer such that $g^{a}\in H$. Therefore, $r=0$. Consequently, $g^{n}\in H$ only if $n=qa$, and $H=\langle g^{a}\rangle$ and is cyclic, as was to be shown. ∎

As the alert reader will have noticed, the preceding proof invoked the notion of division with remainder which should be familiar from number theory. Our treatment of cyclic groups will have close ties with notions from number theory. This is no coincidence, as the next few statements will show. Indeed, an alternative title for this section could have been "Modular arithmetic and integer ideals". The notion of an ideal may not yet be familiar to the reader, who is asked to wait patiently until the chapter about rings.

Theorem 4: Let $\mathbb {Z} _{n}=\{0,1,2,...,n-1\}$ with addition defined modulo $n$. That is $a+b\equiv r\,\mathrm {mod} \,n$, where $a+b=qn+r$. We denote this operation by $a+_{n}b=r$. Then $(\mathbb {Z} _{n},+_{n})$ is a cyclic group.

Proof: We must first show that $(\mathbb {Z} _{n},+_{n})$ is a group, then find a generator. We verify the group axioms. Associativity is inherited from the integers. The element $0\in Z_{n}$ is an identity element with respect to $+_{n}$. An inverse of $a\in Z_{n}$ is an element $b$ such that $a+_{n}b=0$. Thus $b+a|n$. Then, $b\equiv n-a\equiv -a\,\mathrm {mod} \,n$, and so $b=n-a=-a$, and $(\mathbb {Z} _{n},+_{n})$ is a group. Now, since $a=a\cdot 1=\underbrace {1+...+1} _{a\,\mathrm {terms} }$, $1$ generates $\mathbb {Z} _{n}$ and so $(\mathbb {Z} _{n},+_{n})$ is cyclic. ∎

Unless we explicitly state otherwise, by $\mathbb {Z} _{n}$ we will always refer to the cyclic group $(\mathbb {Z} _{n},+_{n})$. Since the argument for the generator of $\mathbb {Z} _{n}$ can be made valid for any integer $a$, this shows that also $\mathbb {Z}$ is cyclic with the generator $1$.

Theorem 5: An element $a\in \mathbb {Z} _{n}$ is a generator if and only if $\gcd(a,n)=1$.

Proof: We will need the following theorem from number theory: If $m,n$ are integers, then there exists integers $r,s$ such that $rm+sn=1$, if and only if $\gcd(m,n)=1$. We will not prove this here. A proof can be found in the number theory section.

For the right implication, assume that $\langle a\rangle =\mathbb {Z} _{n}$. Then for all $b\in \mathbb {Z} _{n}$, $b\equiv pa\,\mathrm {mod} \,n$ for some integer $p$. In particular, there exists an integer $s$ such that $sa\equiv 1\,\mathrm {mod} \,n$. This implies that there exists another integer $r$ such that $sa-rn=1$. By the above-mentioned theorem from number theory, we then have $\gcd(a,n)=1$. For the left implication, assume $\gcd(a,n)=1$. Then there exists integers $s,r$ such that $sa-rn=1\,\Rightarrow \,sa\equiv 1\,\mathrm {mod} \,n$, implying that $sa=1$ in $\mathbb {Z} _{n}$. Since $1$ generates $\mathbb {Z} _{n}$, it must be true that $a$ is also a generator, proving the theorem. ∎

We can generalize Theorem 5 a bit by looking at the orders of the elements in cyclic groups.

Theorem 6: Let $H=\langle g\rangle \leq \mathbb {Z} _{n}$. Then, $|H|=|a|={\frac {n}{\gcd(a,n)}}$.

Proof: Recall that the order of $a\in \mathbb {Z} _{n}$ is defined as the lowest positive integer $r$ such that $ra=0$ in $\mathbb {Z} _{n}$. Since $\langle g\rangle$ is cyclic, there exists an integer $s$ such that $ra=sn$ is minimal and positive. This is the definition of the least common multiple; $\mathrm {lcm} (a,n)=ra=|a|a$. Recall from number theory that $\mathrm {lcm} (a,n)\cdot \gcd(a,n)=an$. Thus, $|a|={\frac {\mathrm {lcm} (a,n)}{a}}={\frac {an}{a\cdot \gcd(a,n)}}={\frac {n}{\gcd(a,n)}}$, as was to be proven. ∎

Theorem 7: Every subgroup of $\mathbb {Z}$ is of the form $n\mathbb {Z} =\{na\mid a\in \mathbb {Z} \}$.

Proof: The fact that any subgroup of $\mathbb {Z}$ is cyclic follows from Theorem 3. Therefore, let $n$ generate $H\leq \mathbb {Z}$. Then we see immediately that $H=n\mathbb {Z}$. ∎

Theorem 8: Let $a,b\in \mathbb {Z}$ be fixed, and let $H=\{ra+sb|r,s\in \mathbb {Z} \}$. Then $H$ is a subgroup of $\mathbb {Z}$ generated by $\gcd(a,b)$.

Proof: We msut first show that $H$ is a subgroup. This is immediate since $(ra+sb)-(r^{\prime }a+s^{\prime }b)=(r-r^{\prime })a+(s-s^{\prime })b\in H$. From the proof of Theorem 3, we see that any subgroup of $\mathbb {Z}$ is generated by its lowest positive element. It is a theorem of number theory that the lowest positive integer $d$ such that $d=ra+sb$ for fixed integers $a,b$ and $r,s\in \mathbb {Z}$ equals the greatest common divisor of $a$ and $b$ or $\gcd(a,b)$. Thus $\gcd(a,b)$ generates $H$. ∎

Theorem 9: Let $n\mathbb {Z}$ and $m\mathbb {Z}$ be subgroups of $\mathbb {Z}$. Then $n\mathbb {Z} \cap m\mathbb {Z}$ is the subgroup generated by $\mathrm {lcm} (n,m)$.

Proof: The fact that $n\mathbb {Z} \cap m\mathbb {Z}$ is a subgroup is obvious since $n\mathbb {Z}$ and $m\mathbb {Z}$ are subgroups. To find a generator of $n\mathbb {Z} \cap m\mathbb {Z}$, we must find its lowest positive element. That is, the lowest positive integer $p$ such that $p$ is both a multiple of $n$ and of $m$. This is the definition of the least common multiple of $n$ and $m$, or $\mathrm {lcm} (n,m)$, and the result follows. ∎

It should be obvious by now that $C_{n}$ and $\mathbb {Z} _{n}$, and $C_{\infty }$ and $\mathbb {Z}$ are the same groups. This will be made precise in a later section but can be visualized by denoting any generator of $C_{n}$ or $C_{\infty }$ by $1$.

We will have more to say about cyclic groups later, when we have more tools at our disposal.

Group Theory/Permutation groups

Permutation Groups

For any finite non-empty set S, A(S) the set of all 1-1 transformations (mapping) of S onto S forms a group called Permutation group and any element of A(S) i.e., a mapping from S onto itself is called Permutation.

Symmetric groups

Theorem 1: Let $A$ be any set. Then, the set $S_{A}$ of bijections from $A$ to itself, $f\,:,A\rightarrow A$, form a group under composition of functions.

Proof: We have to verify the group axioms. Associativity is fulfilled since composition of functions is always associative: $(f\circ g)\circ h(x)=f\circ g(h(x))=f(g(h(x)))=f(g\circ h(x))=f\circ (g\circ h)(x)$ where the composition is defined. The identity element is the identity function given by $\mathrm {id} _{A}(a)=a$ for all $a\in A$. Finally, the inverse of a function $f$ is the function $f^{-1}$ taking $f(a)$ to $a$ for all $a\in A$. This function exists and is unique since $f$ is a bijection. Thus $S_{A}$ is a group, as stated. ∎

$S_{A}$ is called the symmetric group on $A$. When $A=\{1,2,...,n\}\,,\,n\in \mathbb {N}$, we write its symmetric group as $S_{n}$, and we call this group the symmetric group on $n$ letters. It is also called the group of permutations on $n$ letters. As we will see shortly, this is an appropriate name.

Instead of $e$, we will use a different symbol, namely $\iota$, for the identity function in $S_{n}$.

When $\sigma \in S_{n}$, we can specify $\sigma$ by specifying where it sends each element. There are many ways to encode this information mathematically. One obvious way is to identify $\sigma$ as the unique $n\times n$ matrix with value $1$ in the entries $(i,\sigma (i))$ and $0$ elsewhere. Composition of functions then corresponds to multiplication of matrices. Indeed, the matrix corresponding to $\rho$ has value $1$ in the entries $(i,\rho (i))$, which is the same as $(\sigma (j),\rho (\sigma (j)))$, so the product has value $1$ in the entries $(j,\rho (\sigma (j)))$. This notation may seem cumbersome. Luckily, there exists a more convenient notation, which we will make use of.

We can represent any $\sigma \in S_{n}$ by a $2\times n$ matrix $\left({\begin{array}{cccc}1&2&\dots &n\\\sigma (1)&\sigma (2)&\dots &\sigma (n)\end{array}}\right)$. We obviously lose the correspondence between function composition and matrix multiplication, but we gain a more readable notation. For the time being, we will use this.

Remark 2: Let $\sigma ,\rho \in S_{n}$. Then the product $\sigma \rho \equiv \sigma \circ \rho$ is the function obtained by first acting with $\rho$, and then by $\sigma$. That is, $\sigma \rho (x)=\sigma (\rho (x))$. This point is important to keep in mind when computing products in $S_{n}$. Some textbooks try to remedy the frequent confusion by writing functions like $(x)\rho \sigma$, that is, writing arguments on the left of functions. We will not do this, as it is not standard. The reader should use the next example and theorem to get a feeling for products in $S_{n}$.

Example 3: We will show the multiplication table for $S_{3}$. We introduce the special notation for $S_{3}$: $\iota =\rho _{0}$, $\rho _{1}=\left({\begin{array}{ccc}1&2&3\\2&3&1\end{array}}\right)$, $\rho _{2}=\left({\begin{array}{ccc}1&2&3\\3&1&2\end{array}}\right)$, $\mu _{1}=\left({\begin{array}{ccc}1&2&3\\1&3&2\end{array}}\right)$, $\mu _{2}=\left({\begin{array}{ccc}1&2&3\\3&2&1\end{array}}\right)$ and $\mu _{3}=\left({\begin{array}{ccc}1&2&3\\2&1&3\end{array}}\right)$. The multiplication table for $S_{3}$ is then

${\begin{array}{c|cccccc}\circ &\rho _{0}&\rho _{1}&\rho _{2}&\mu _{1}&\mu _{2}&\mu _{3}\\\hline \rho _{0}&\rho _{0}&\rho _{1}&\rho _{2}&\mu _{1}&\mu _{2}&\mu _{3}\\\rho _{1}&\rho _{1}&\rho _{2}&\rho _{0}&\mu _{3}&\mu _{1}&\mu _{2}\\\rho _{2}&\rho _{2}&\rho _{0}&\rho _{1}&\mu _{2}&\mu _{3}&\mu _{1}\\\mu _{1}&\mu _{1}&\mu _{2}&\mu _{3}&\rho _{0}&\rho _{2}&\rho _{1}\\\mu _{2}&\mu _{2}&\mu _{3}&\mu _{1}&\rho _{1}&\rho _{0}&\rho _{2}\\\mu _{3}&\mu _{3}&\mu _{1}&\mu _{2}&\rho _{2}&\rho _{1}&\rho _{0}\end{array}}$

Theorem 4: $S_{n}$ has order $n!$.

Proof: This follows from a counting argument. We can specify a unique element in $S_{n}$ by specifying where each $i\in \{1,2,...,n\}$ is sent. Also, any permutation can be specified this way. Let $\sigma \in S_{n}$. In choosing $\sigma (1)$ we are completely free and have $n$ choices. Then, when choosing $\sigma (2)$ we must choose from $\{1,...,n\}-\{\sigma (1)\}$, giving a total of $n-1$ choices. Continuing in this fashion, we see that for $\sigma (i)$ we must choose from $\{1,...,n\}-\{\sigma (1),...,\sigma (i-1)\}$, giving a total of $n+1-i$ choices. The total number of ways in which we can specify an element, and thus the number of elements in $S_{n}$ is then $|S_{n}|=\prod _{i=1}^{n}(n+1-i)=n(n-1)...\cdot 2\cdot 1=n!$, as was to be shown. ∎

Theorem 5: $S_{n}$ is non-abelian for all $n\geq 3$.

Proof: Let $\sigma =\left({\begin{array}{ccccc}1&2&3&\dots &n\\2&1&3&\dots &n\end{array}}\right)$ be the function only interchanging 1 and 2, and $\rho =\left({\begin{array}{ccccc}1&2&3&\dots &n\\1&3&2&\dots &n\end{array}}\right)$ be the function only interchanging 2 and 3. Then $\sigma \rho =\left({\begin{array}{ccccc}1&2&3&\dots &n\\2&3&1&\dots &n\end{array}}\right)$ and $\rho \sigma =\left({\begin{array}{ccccc}1&2&3&\dots &n\\3&1&2&\dots &n\end{array}}\right)$. Since $\sigma \rho \neq \rho \sigma$, $S_{n}$ is not abelian. ∎

Definition 6: Let $\sigma \in S_{n}$ such that $\sigma ^{k}=\iota$ for some $k\in \mathbb {Z}$. Then $\sigma$ is called an $k$-cycle, where $k$ is the smallest positive such integer. Let $\sigma ^{*}$ be the set of integers $a$ such that $\sigma (a)\neq a$. Two cycles $\sigma ,\rho$ are called disjoint if $\sigma ^{*}\cap \rho ^{*}=\emptyset$. Also, a 2-cycle is called a transposition.

Remark 3: It's important to realize that if $a\in \sigma ^{*}$, then so is $\sigma (a)$. If $\sigma (a)=b\neq a$, then if $\sigma (b)=b$ we have that $\sigma$ is not 1–1.

Theorem 7: Let $\sigma ,\rho \in S_{n}$. If $\sigma ^{*}\cap \rho ^{*}=\emptyset$, then $\sigma \rho =\rho \sigma$.

Proof: For any integer $1\leq a\leq n$ such that $a\in \sigma ^{*}$ but $a\not \in \rho ^{*}$ we have $\sigma \rho (a)=\sigma (\iota (a))=\sigma (a)=\iota (\sigma (a))=\rho (\sigma (a))=\rho \sigma (a)$. A similar argument holds for $a\in \rho ^{*}$ but $a\not \in \sigma ^{*}$. If $a\not \in \sigma ^{*}\cup \rho ^{*}$, we must have $\sigma \rho (a)=\sigma (a)=a=\rho (a)=\rho \sigma (a)$. Since $\sigma ^{*}\cap \rho ^{*}=\emptyset$, we have now exhausted every $a\in \{1,...,n\}$, and we are done. ∎

Theorem 8: Any permutation can be represented as a composition of disjoint cycles.

Proof: Let $\sigma \in S_{n}$. Choose an element $a\in \sigma ^{*}$ and compute $\sigma (a),\sigma ^{2}(a),...,\sigma ^{k}(a)=a$. Since $S_{n}$ is finite of order $n!$, we know that $k$ exists and $k\leq n!$. We have now found a $k$-cycle $\sigma _{1}$ including $a$. Since $\sigma _{1}^{*}=\{a,\sigma (a),...,\sigma ^{k-1}(a)\}$, this cycle may be factored out from $\sigma$ to obtain $\sigma =\sigma _{1}\sigma ^{\prime }$. Repeat this process, which terminates since $\sigma ^{*}$ is finite, and we have constructed a composition of disjoint cycles that equals $\sigma$. ∎

Now that we have shown that all permuations are just compositions of disjoint cycles, we can introduce the ultimate shorthand notation for permutations. For an $n$-cycle $\sigma$, we can show its action by choosing any element $a\in \sigma ^{*}$ and writing $\sigma =\left(a\ \sigma (a)\ \sigma ^{2}(a)\ ...\ \sigma ^{n-1}(a)\right)$.

Theorem 9: Any $n$-cycle can be represented as a composition of transpositions.

Proof: Let $\sigma =\left(a\ \sigma (a)\ \sigma ^{2}(a)\ ...\ \sigma ^{n-1}(a)\right)$. Then, $\sigma =\left(a\ \sigma ^{2}(a)\ ...\ \sigma ^{n-1}(a)\right)\left(a\ \sigma (a)\right)$ (check this!), omitting the composition sign $\circ$. Interate this process to obtain $\sigma =\left(a\ \sigma ^{n-1}(a)\right)...\left(a\ \sigma ^{2}(a)\right)\left(a\ \sigma (a)\right)$. ∎

Note 10: This way of representing $\sigma$ as a product of transpositions is not unique. However, as we will see now, the "parity" of such a representation is well defined.

Definition 11: The parity of a permutation is even if it can be expressed as a product of an even number of transpositions. Otherwise, it is odd. We define the function $\operatorname {sgn}(\sigma )=1$ if $\sigma$ is even and $\operatorname {sgn}(\sigma )=-1$ if $\sigma$ is odd.

Lemma 12: The identity $\iota$ has even parity.

Proof: Observe first that $\iota \neq (a\ b)$ for $a\neq b$. Thus the minimum number of transpositions necessary to represent $\iota$ is 2: $\iota =(a\ b)(a\ b)$. Now, assume that for any representation using less than $k$ transpositions must be even. Thus, let $\iota =(a_{1}\ b_{1})...(a_{k}\ b_{k})$. Now, since in particular $\iota (a_{1})=a_{1}$, we must have $a_{1}\in (a_{i}\ b_{i})^{*}$ for some $1<i\leq k$. Since disjoint transpositions commute, and $(a_{r}\ a_{s})(a_{i}\ a_{r})=(a_{i}\ a_{s})(a_{r}\ a_{s})$ where $a_{i}\neq a_{r}\neq a_{s}$, it is always possible to configure the transpositions such that the first two transpositions are either $(a_{1}\ b_{1})(a_{1}\ b_{1})=\iota$, reducing the number of transposition by two, or $(a_{1}\ b_{1})(a_{1}\ b_{2})=(a_{1}\ b_{2})(b_{1}\ b_{2})$. In this case we have reduced the number of transpositions involving $a_{1}$ by 1. We restart the same process as above. with the new representation. Since only a finite number of transpositions move $a_{1}$, we will eventually be able to cancel two permutations and be left with $k-2$ transpositions in the product. Then, by the induction hypothesis, $k-2$ must be even and so $k$ is even as well, proving the lemma. ∎

Theorem 13: The parity of a permutation, and thus the $\operatorname {sgn}$ function, is well-defined.

Proof: Let $\sigma \in S_{n}$ and write $\sigma$ as a product of transposition in two different ways: $\sigma =\tau _{1}...\tau _{k}=\tau _{1}^{\prime }...\tau _{k^{\prime }}^{\prime }$. Then, since $\iota$ has even parity by Lemma 11 and $\iota =\sigma \sigma ^{-1}=\tau _{1}...\tau _{k}\tau _{k^{\prime }}^{\prime }...\tau _{1}^{\prime }$. Thus, $k+k^{\prime }\equiv 0\ \mathrm {mod} \ 2$, and $k\equiv k^{\prime }\ \mathrm {mod} \ 2$, so $\sigma$ has a uniquely defined parity, and consequentially $\operatorname {sgn}$ is well-defined. ∎

Theorem 14: Let $\sigma ,\rho \in S_{n}$. Then, $\operatorname {sgn}(\sigma \rho )=\operatorname {sgn}(\sigma )\operatorname {sgn}(\rho )$.

Proof: Decompose $\sigma$ and $\rho$ into transpositions: $\sigma =\mu _{1}...\mu _{k}$, $\rho =\nu _{1}...\nu _{l}$. Then $\sigma \rho =\mu _{1}...\mu _{k}\nu _{1}...\nu _{l}$ has parity given by $k+l$. If both are even or odd, $k+l$ is even and indeed $\operatorname {sgn}(\sigma )\operatorname {sgn}(\rho )=1\cdot 1=1=\operatorname {sgn}(\sigma \rho )$. If one is odd and one is even, $k+l$ is odd and again $\operatorname {sgn}(\sigma )\operatorname {sgn}(\rho )=(-1)\cdot 1=-1=\operatorname {sgn}(\sigma \rho )$, proving the theorem. ∎

Lemma 15: The number of even permutations in $S_{n}$ equals the number of odd permutations.

Proof: Let $\sigma$ be any even permutation and $\tau$ a transposition. Then $\tau \sigma$ has odd parity by Theorem 14. Let $E$ be the set of even permutations and $O$ the set of odd permutations. Then the function $f:E\rightarrow O$ given by $f(\sigma )=\tau \sigma$ for any $\sigma \in E$ and a fixed transposition $\tau$, is a bijection. (Indeed, it is a transposition in $S_{S_{n}}$!) Thus $E$ and $O$ have the same number of elements, as stated. ∎

Definition 16: Let the set of all even permutations in $S_{n}$ be denoted by $A_{n}$. $A_{n}$ is called the alternating group on $n$ letters.

Theorem 17: $A_{n}$ is a group, and is a subgroup of $S_{n}$ of order ${\frac {n!}{2}}$.

Proof: We first show that $A_{n}$ is a group under composition. Then it is automatically a subgroup of $S_{n}$. That $A_{n}$ is closed under composition follows from Theorem 14 and associativity is inherited from $S_{n}$. Also, the identity permutation is even, so $\iota \in A_{n}$. Thus $A_{n}$ is a group and a subgroup of $S_{n}$. Since the number of even and odd permutations are equal by Lemma 14, we then have that $|A_{n}|={\frac {|S_{n}|}{2}}={\frac {n!}{2}}$, proving the theorem. ∎

Theorem 18: Let $n\geq 3$. Then $A_{n}$ is generated by the 3-cycles in $S_{n}$.

Proof: We must show that any even permutation can be decomposed into 3-cycles. It is sufficient to show that this is the case for pairs of transpositions. Let $a,b,c,d\in S_{n}$ be distinct. Then, by some casework,

i) $(a\ b)(a\ b)=(a\ b\ c)^{3}$,

ii) $(a\ b)(b\ c)=(c\ a\ b)$, and

iii) $(a\ b)(c\ d)=(a\ d\ c)(a\ b\ c)$,

proving the theorem. ∎

In a previous section we proved Lagrange's Theorem: The order of any subgroup divides the order of the parent group. However, the converse statement, that a group has a subgroup for every divisor of its order, is false! The smallest group providing a counterexample is the alternating group $A_{4}$, which has order 12 but no subgroup of order 6. It has subgroups of orders 3 and 4, corresponding respectively to the cyclic group of order 3 and the Klein 4-group. However, if we add any other element to the subgroup corresponding to $C_{3}$, it generates the whole group $A_{4}$. We leave it to the reader to show this.

Dihedral Groups

The lines represent the reflection symmetries of a regular hexagon

Illustration of the elements of the dihedral group $D_{16}$ as rotations and reflections of a stop sign.

The dihedral groups are the symmetry groups of regular polygons. As such, they are subgroups of the symmetric groups. In general, a regular $n$-gon has $n$ rotational symmetries and $n$ reflection symmetries. The dihedral groups capture these by consisting of the associated rotations and reflections.

Definition 19: The dihedral group of order $2n$, denoted $D_{2n}$, is the group of rotations and reflections of a regular $n$-gon.

Theorem 20: The order of $D_{2n}$ is precisely $2n$.

Proof: Let $\rho$ be a rotation that generates a subgroup of order $n$ in $D_{2n}$. Obviously, $\langle \rho \rangle$ then captures all the pure rotations of a regular $n$-gon. Now let $\mu$ be any rotation in The rest of the elements can then be found by composing each element in $\langle \rho \rangle$ with $\mu$. We get a list of elements $D_{2n}=\{\iota ,\rho ,...,\rho ^{n-1},\mu ,\mu \rho ,...,\mu \rho ^{n-1}\}$. Thus, the order of $D_{2n}$ is $2n$, justifying its notation and proving the theorem. ∎

Remark 21: From this proof we can also see that $\{\rho ,\mu \}$ is a generating set for $G$, and all elements can be obtained by writing arbitrary products of $\rho$ and $\mu$ and simplifying the expression according to the rules $\rho ^{n}=\iota$, $\mu ^{2}=\iota$ and $\rho \mu =\mu \rho ^{-1}$. Indeed, as can be seen from the figure, a rotation composed with a reflection is new reflection.

Group Theory/Homomorphism

We are finally making our way into the meat of the theory. In this section we will study structure-preserving maps between groups. This study will open new doors and provide us with a multitude of new theorems.

Up until now we have studied groups at the "element level". Since we are now about to take a step back and study groups at the "homomorphism level", readers should expect a sudden increase in abstraction starting from this section. We will try to ease the reader into this increase by keeping one foot at the "element level" throughout this section.

From here on out the notation $e_{G}$ will denote the identity element in the group $G$ unless otherwise specified.

Group homomorphisms

Definition 1: Let $(G,*)$ and $(H,\cdot )$ be groups. A homomorphism from $G$ to $H$ is a function $\phi \,:\,G\rightarrow H$ such that for all $g_{1},g_{2}\in G$,

$\phi (g_{1}*g_{2})=\phi (g_{1})\cdot \phi (g_{2})$.

Thus, a homomorphism preserves the group structure. We have included the multiplication symbols here to make explicit that multiplication on the left side occurs in $G$, and multiplication on the right side occurs in $H$.

Already we see that this section is different from the previous ones. Up until now we have, excluding subgroups, only dealt with one group at a time. No more! Let us start by deriving some elementary and immediate consequences of the definition.

Theorem 2: Let $G,H$ be groups and $\phi \,:\,G\rightarrow H$ a homomorphism. Then $\phi (e_{G})=e_{H}$. In other words, the identity is mapped to the identity.

Proof: Let $g\in G$. Then, $\phi (g)=\phi (e_{G}g)=\phi (e_{G})\phi (g)$, implying that $\phi (e_{G})$ is the identity in $H$, proving the theorem. ∎

Theorem 3: Let $G,H$ be groups and $\phi \,:\,G\rightarrow H$ a homomorphism. Then for any $g\in G$, $\phi (g^{-1})=\phi (g)^{-1}$. In other words, inverses are mapped to inverses.

Proof: Let $g\in G$. Then $e_{H}=\phi (e_{G})=\phi (gg^{-1})=\phi (g)\phi (g^{-1})$ implying that $\phi (g^{-1})=\phi (g)^{-1}$, as was to be shown. ∎

Theorem 4: Let $G,G^{\prime }$ be groups, $\phi \,:\,G\rightarrow G^{\prime }$ a homomorphism and let $H$ be a subgroup of $G$. Then $\phi (H)=\{\phi (h)\mid h\in H\}$ is a subgroup of $G^{\prime }$.

Proof: Let $h_{1},h_{2}\in H$. Then $\phi (h_{1}),\phi (h_{2})\in \phi (H)$ and $\phi (h_{1})\phi (h_{2})^{-1}=\phi (h_{1})\phi (h_{2}^{-1})=\phi (h_{1}h_{2}^{-1})$. Since $h_{1}h_{2}^{-1}\in H$, $\phi (h_{1})\phi (h_{2})^{-1}=\phi (h_{1}h_{2}^{-1})\in \phi (H)$, and so $\phi (H)$ is a subgroup of $G^{\prime }$. ∎

Theorem 5: Let $G,G^{\prime }$ be groups, $\phi \,:\,G\rightarrow G^{\prime }$ a homomorphism and let $H^{\prime }$ be a subgroup of $G^{\prime }$. Then $\phi ^{-1}(H^{\prime })=\{g\in G\mid \phi (g)\in H^{\prime }\}$ is a subgroup of $G$.

Proof: Let $g_{1},g_{2}\in \phi ^{-1}(H^{\prime })$. Then $\phi (g_{1}),\phi (g_{2})\in H^{\prime }$, and since $H^{\prime }$ is a subgroup, $\phi (g_{1})\phi (g_{2})^{-1}=\phi (g_{1})\phi (g_{2}^{-1})=\phi (g_{1}g_{2}^{-1})\in H^{\prime }$. But then, $g_{1}g_{2}^{-1}\in \phi ^{-1}(H^{\prime })$, and so $\phi ^{-1}(H^{\prime })$ is a subgroup of $G$. ∎

From Theorem 4 and Theorem 5 we see that homomorphisms preserve subgroups. Thus we can expect to learn a lot about the subgroup structure of a group $G$ by finding suitable homomorphisms into $G$.

In particular, every homomorphism $\phi \,:\,G\rightarrow G^{\prime }$ has associated with it two important subgroups.

Definition 6: A homomorphism is called an isomorphism if it is bijective and its inverse is a homomorphism. Two groups are called isomorphic if there exists an isomorphism between them, and we write $G\approx H$ to denote "$G$ is isomorphic to $H$".

Theorem 7: A bijective homomorphism is an isomorphism.

Proof: Let $G,H$ be groups and let $\phi \,:\,G\rightarrow H$ be a bijective homomorphism. We must show that the inverse $\phi ^{-1}$ is a homomorphism. Let $h_{1},h_{2}\in H$. then there exist unique $g_{1},g_{2}\in G$ such that $\phi (g_{1})=h_{1}$ and $\phi (g_{2})=h_{2}$. Then we have $\phi (g_{1}g_{2})=h_{1}h_{2}$ since $\phi$ is a homomorphism. Now apply $\phi ^{-1}$ to all equations. We obtain $\phi ^{-1}(h_{1})=g_{1}$, $\phi ^{-1}(h_{2})=g_{2}$ and $\phi ^{-1}(h_{1}h_{2})=g_{1}g_{2}=\phi ^{-1}(h_{1})\phi ^{-1}(h_{2})$, so $\phi ^{-1}$ is a homomorphism and thus $\phi$ is an isomorphism. ∎

Definition 8: Let $G,G^{\prime }$ be groups. A homomorphism that maps every element in $G$ to $e^{\prime }\in G^{\prime }$ is called a trivial homomorphism (or zero homomorphism), and is denoted by $0_{GG^{\prime }}\,:\,G\rightarrow G^{\prime }$

Definition 9: Let $H$ be a subgroup of a group $G$. Then the homomorphism $i\,:\,H\rightarrow G$ given by $i(h)=h$ is called the inclusion of $H$ into $G$. Let $G^{\prime }$ be a group isomorphic to a subgroup $H$ of a group $G$. Then the isomorphism $\phi \,:\,G^{\prime }\rightarrow H$ induces an injective homomorphism $i^{\prime }\,:\,G^{\prime }\rightarrow G$ given by $i^{\prime }(g^{\prime })=\phi (g^{\prime })$, called an imbedding of $G^{\prime }$ into $G$. Obviously, $i^{\prime }=i\circ \phi$.

Definition 10: Let $G,G^{\prime }$ be groups and $\phi \,:\,G\rightarrow G^{\prime }$ a homomorphism. Then we define the following subgroups:

i) $\ker \,\phi =\{g\in G\mid \phi (g)=e^{\prime }\}\leq G$, called the kernel of $\phi$, and

ii) $\mathrm {im} \,\phi =\{g^{\prime }\in G^{\prime }\mid (\exists g\in G)\phi (g)=g^{\prime }\}\leq G^{\prime }$, called the image of $\phi$.

Theorem 11: The composition of homomorphisms is a homomorphism.

Proof: Let $G,H,K$ be groups and $\phi \,:\,G\rightarrow H$ and $\psi \,:\,H\rightarrow K$ homomorphisms. Then $\psi \circ \phi \,:\,G\rightarrow K$ is a function. We must show it is a homomorphism. Let $g,h\in G$. Then $\psi \circ \phi (gh)=\psi (\phi (gh))=\psi (\phi (g)\phi (h))=\psi (\phi (g))\psi (\phi (h))=\psi \circ \phi (g)\psi \circ \phi (h)$, so $\psi \circ \phi$ is indeed a homomorphisms. ∎

Theorem 12: Composition of homomorphisms is associative.

Proof: This is evident since homomorphisms are functions, and composition of functions is associative. ∎

Corollary 13: The composition of isomorphisms is an isomorphism.

Proof: This is evident from Theorem 11 and since the composition of bijections is a bijection. ∎

Theorem 14: Let $G,H$ be groups and $\phi \,:\,G\rightarrow H$ a homomorphism. Then $\phi$ is injective if and only if $\ker \,\phi =\{e\}\subseteq G$.

Proof: Assume $\ker \,\phi =\{e\}$ and $g_{1},g_{2}\in G$. Then $\phi (g_{1})=\phi (g_{2})\,\Leftrightarrow \phi (g_{1})\phi (g_{2})^{-1}=\phi (g_{1}g_{2}^{-1})=e_{H}$, implying that $g_{1}g_{2}^{-1}\in \ker \,\phi$. But by assumption then $g_{1}g_{2}^{-1}=e\,\Leftrightarrow g_{1}=g_{2}$, so $\phi$ is injective. Assume now that $\ker \,\phi \neq \{e\}$ and $g\in G$. Then there exists another element $k\in \ker \,\phi$ such that $k\neq e$. But then $\phi (g)=\phi (kg)$. Since both $g$ and $kg\neq g$ map to $\phi (g)=\phi (kg)$, $\phi$ is not injective, proving the theorem. ∎

Corollary 15: Inclusions are injective.

Proof: The result is immediate. Since $i(h)=h$ for all $h\in H\leq G$, we have $i^{-1}(e)=\{e\}$. ∎

The kernel can be seen to satisfy a universal property. The following theorem explains this, but it is unusually abstract for an elementary treatment of groups, and the reader should not worry if he/she cannot understand it immediately.

Commutative diagram showing the universal property of kernels.

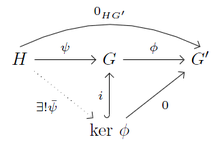
Theorem 16: Let $G,G^{\prime }$ be groups and $\phi \,:\,G\rightarrow G^{\prime }$ a group homomorphism. Also let $H$ be a group and $\psi \,:\,H\rightarrow G$ a homomorphism such that $\phi \circ \psi =0_{HG^{\prime }}$. Also let $i\,:\,\ker \,\phi \rightarrow G$ is the inclusion of $\ker \,\phi$ into $G$. Then there exists a unique homomorphism ${\bar {\psi }}\,:\,H\rightarrow \ker \,\phi$ such that$\psi =i\circ {\bar {\psi }}$.

Proof: Since $\phi \circ \psi =0_{HG^{\prime }}$, by definition we must have $\psi (H)\leq \ker \,\phi$, so ${\bar {\psi }}$ exists. The commutativity $\psi =i\circ {\bar {\psi }}$ then forces ${\bar {\psi }}(h)=\psi (h)\in \ker \,\phi$, so ${\bar {\psi }}$ is unique. ∎

Definition 17: A commutative diagram is a pictorial presentation of a network of functions. Commutativity means that when several routes of function composition from one object lead to the same destination, the two compositions are equal as functions. As an example, the commutative diagram on the right describes the situation in Theorem 16. In the commutative diagrams (or diagrams for short, we will not show diagrams which no not commute) shown in this chapter on groups, all functions are implicitly assumed to be group homomorphisms. Monomorphisms in diagrams are often emphasized by hooked arrows. In addition, epimorphims are often emphasized by double headed arrows. That an inclusion is a monomorphism will be proven shortly.

Remark 18: From the commutative diagram on the right, the kernel can be defined completely without reference to elements. Indeed, Theorem 16 would become the definition, and our Definition 10 i) would become a theorem. We will not entertain this line of thought in this book, but the advanced reader is welcome to work it out for him/herself.

Automorphism Groups

In this subsection we will take a look at the homomorphisms from a group to itself.

Definition 19: A homomorphism from a group $G$ to itself is called an endomorphism of $G$. An endomorphism which is also an isomorphism is called an automorphism. The set of all endomorphisms of $G$ is denoted $\mathrm {End} (G)$, while the set of all automorphisms of $G$ is denoted $\mathrm {Aut} (G)$.

Theorem 20: $\mathrm {End} (G)$ is a monoid under composition of homomorphisms. Also, $\mathrm {Aut} (G)$ is a submonoid which is also a group.

Proof: We only have to confirm that $\mathrm {End} (G)$ is closed and has an identity, which we know is true. For $\mathrm {Aut} (G)$, the identity homomorphism $\mathrm {id} _{G}\,:\,G\rightarrow G$ is an isomorphism and the composition of isomorphisms is an isomorphism. Thus $\mathrm {Aut} (G)$ is a submonoid. To show it is a group, note that the inverse of an automorphism is an automorphism, so $\mathrm {Aut} (G)$ is indeed a group. ∎

Groups with Operators

An endomorphism of a group can be thought of as a unary operator on that group. This motivates the following definition:

Definition 21: Let $G$ be a group and $\Omega \subset \mathrm {End} (G)$. Then the pair $(G,\Omega )$ is called a group with operators. $\Omega$ is called the operator domain and its elements are called the homotheties of $G$. For any $\omega \in \Omega$, we introduce the shorthand $\omega (g)=g^{\omega }$ for all $g\in G$. Thus the fact that the homotheties of $G$ are endomorphisms can be expressed thus: for all $a,b\in G$ and $\omega \in \Omega$, $(ab)^{\omega }=a^{\omega }b^{\omega }$.

Example 22: For any group $G$, the pair $(G,\emptyset )$ is trivially a group with operators.

Lemma 23: Let $(G,\Omega )$ be a group with operators. Then $\Omega$ can be extended to a submonoid $\Omega ^{\prime }$ of $\mathrm {End} (G)$ such that the structure of $(G,\Omega ^{\prime })$ is identical to $(G,\Omega )$.

Proof: Let $\Omega ^{\prime }$ include the identity endomorphism and let $\Omega$ be a generating set. Then $\Omega ^{\prime }$ is closed under compositions and is a monoid. Since any element of $\Omega ^{\prime }$ is expressible as a (possibly empty) composition of elements in $\Omega$, the structures are identical. ∎

In the following, we assume that the operator domain is always a monoid. If it is not, we can extend it to one by Lemma 23.

Definition 24: Let $(G,\Omega )$ and $(H,\Omega )$ be groups with operators with the same operator domain. Then a homomorphism $\phi \,:\,(G,\Omega )\rightarrow (H,\Omega )$ is a group homomorphism $\phi \,:\,G\rightarrow H$ such that for all $\omega \in \Omega$ and $g\in G$, we have $\phi (g^{\omega })=\phi (g)^{\omega }$.

Definition 25: Let $(G,\Omega )$ be a group with operators and $H$ a subgroup of $G$. Then $H$ is called a stable subgroup (or a $\Omega$-invariant subgroup) if for all $h\in H$ and $\omega \in \Omega$, $h^{\omega }\in H$. We say that $H$ respects the homotheties of $G$. In this case $(H,\Omega )$ is a sub-group with operators.

Example 26: Let $V$ be a vector space over the field $F$. If we by $V_{+}$ denote the underlying abelian group under addition, then $V=(V_{+},F)$ is a group with operators, where for any $k\in F$ and $v\in V_{+}$, we define $v^{k}=kv$. Then the stable subgroups are precisely the linear subspaces of $V$ (show this).

Problems

Problem 1: Show that there is no nontrivial homomorphism from $\mathbb {Z} _{5}$ to $S_{3}$.

Group Theory/Normal subgroups and Quotient groups

In the preliminary chapter we discussed equivalence classes on sets. If the reader has not yet mastered this notion, he/she is advised to do so before starting this section.

Normal Subgroups

Recall the definition of kernel in the previous section. We will exhibit an interesting feature it possesses. Namely, let $ak\,,\,k\in \ker \,\phi \leq G$ be in the coset $a\ker \,\phi$. Then there exists a $k^{\prime }\in \ker \,\phi$ such that $k^{\prime }a=ak$ for all $a\in G$. This is easy to see because a coset of the kernel includes all elements in $G$ that are mapped to a particular element. The kernel inspires us to look for what are called normal subgroups.

Definition 1: A subgroup $N\leq G$ is called normal if $gNg^{-1}=N$ for all $g\in G$. We may sometimes write $N\trianglelefteq G$ to emphasize that $N$ is normal in $G$.

Theorem 2: A subgroup $N\leq G$ is normal if and only if $gN=Ng$ for all $g\in G$.

Proof: By the definition, a subgroup is normal if and only if $gNg^{-1}=N$ since conjugation is a bijection. The theorem follows by multiplying on the right by $g$. ∎

We stated that the kernel is a normal subgroup in the introduction, so we had better well prove it!

Theorem 3: Let $\phi \,:\,G\rightarrow G^{\prime }$ be any homomorphism. Then $\ker \phi \leq G$ is normal.

Proof: Let $k\in \ker \,\phi$ and $g\in G$. Then $\phi (gkg^{-1})=\phi (g)e^{\prime }\phi (g)^{-1}=e^{\prime }$, so $gkg^{-1}\in \ker \phi$, proving the theorem. ∎

Theorem 4: Let $G,G^{\prime }$ be groups and $\phi \,:\,G\rightarrow G^{\prime }$ a group homomorphism. Then if $H$ is a normal subgroup of $\mathrm {im} \,\phi$, then $\phi ^{-1}(H)$ is normal in $G$.

Proof: Let $g\in G$ and $h\in \phi ^{-1}(H)$. Then $\phi (ghg^{-1})=\phi (g)\phi (h)\phi (g)^{-1}\in H$ since $H$ is normal in $\mathrm {im} \,\phi$, and so $ghg^{-1}\in \phi ^{-1}(H)$, proving the theorem. ∎

Theorem 5: Let $G,G^{\prime }$ be groups and $\phi \,:\,G\rightarrow G^{\prime }$ a group homomorphism. Then if $H$ is a normal subgroup of $G$, $\phi (H)$ is normal in $\mathrm {im} \,\phi$.

Proof: Let $g^{\prime }\in \mathrm {im} \,\phi$ And $h\in H$. Then if $g\in G$ such that $\phi (g)=g^{\prime }$, we have $g^{\prime }\phi (h){g^{\prime }}^{-1}=\phi (g)\phi (h)\phi (g)^{-1}=\phi (ghg^{-1})=\phi (h^{\prime })\in \phi (H)$ for some $h^{\prime }\in H$ since $H$ is normal. Thus $g^{\prime }\phi (H){g^{\prime }}^{-1}=\phi (H)$ for all $g^{\prime }\in \mathrm {im} \,\phi$ and so $H$ is normal in $\mathrm {im} \,\phi$. ∎

Corollary 6: Let $G,G^{\prime }$ be groups and $\phi \,:\,G\rightarrow G^{\prime }$ a surjective group homomorphism. Then if $H$ is a normal subgroup of $G$, $\phi (H)$ is normal in $G^{\prime }$.

Proof: Replace $\mathrm {im} \,\phi$ with $G^{\prime }$ in the proof of Theorem 5. ∎

Remark 7: If $H$ is a normal subgroup of $G$ and $K$ is a normal subgroup of $H$, it does not necessarily imply that $K$ is a normal subgroup of $G$. The reader is invited to display a counterexample of this.

Theorem 8: Let $G$ be a group and $H,K$ be subgroups. Then

i) If $H$ is normal, then $HK=KH$ is a subgroup of $G$.

ii) If both $H$ and $K$ are normal, then $HK=KH$ is a normal subgroup of $G$.

iii) If $H$ and $K$ are normal, then $H\cap K$ is a normal subgroup of $G$.

Proof: i) Let $H$ be normal. First, since for each $k\in K$, there exists $h,h^{\prime }\in H$ such that $kh=h^{\prime }k$, so $KH=HK$. To show $HK$ is a subgroup, let $hk,h^{\prime }k^{\prime }\in HK$. Then $h^{\prime }k^{\prime }(hk)^{-1}=h^{\prime }k^{\prime }k^{-1}h^{-1}=h^{\prime }h^{\prime \prime }k^{\prime }k^{-1}\in HK$ for some $h^{\prime \prime }\in H$ since $H$ is normal, and so $HK$ is a subgroup.

ii) Let $g\in G$ and $hk\in HK$. Then since both $H$ and $K$ are normal, there exists $h^{\prime }\in H\,,\,k^{\prime }\in K$ such that $ghkg^{-1}=ghg^{-1}k^{\prime }=gg^{-1}h^{\prime }k^{\prime }=h^{\prime }k^{\prime }\in HK$. It follows that $gHKg^{-1}=HK$ and so $HK$ is normal.

iii) Let $g\in G$ and $h\in H\cap K$. Then $ghg^{-1}\in H$ since H is normal, and similarly $ghg^{-1}\in K$. Thus $ghg^{-1}\in H\cap K$ and it follows that $H\cap K$ is normal. ∎

Examples of Normal Subgroups

In the following, let $G$ be any group. Then $G$ has associated with it the following normal subgroups.

i) The center of $G$, denoted $Z(G)$, is the subgroup of elements which commute with all others. $Z(G)=\{z\in G\mid (\forall g\in G)zg=gz\}$. That $Z(G)$ is a normal subgroup is easy to verify and is left to the reader.

ii) The commutator subgroup of $G$, denoted $G^{(1)}$ or $[G,G]$, is the subgroup generated by the subset $\{[g,h]\mid g,h\in G\}$ where $[g,h]=g^{-1}h^{-1}gh$ for all $g,h\in G$. For $s\in G$, we introduce the shorthand $sgs^{-1}=g^{s}$. Then we have $s[g,h]s^{-1}=[g^{s},h^{s}]$, such that for any product of commutators $[g_{1},h_{1}][g_{2},h_{2}]...[g_{n},h_{n}]$ where all elements are in $G$, we have $s[g_{1},h_{1}][g_{2},h_{2}]...[g_{n},h_{n}]s^{-1}=[g_{1}^{s},h_{1}^{s}][g_{2}^{s},h_{2}^{s}]...[g_{n}^{s},h_{n}^{s}]$, and so $G^{(1)}$ is normal.

Remark 9: We can iterate the commutator subgroup construction and define $G^{(0)}=G$ and $G^{(n)}=[G^{(n-1)},G^{(n-1)}]$ for all $n\in \mathbb {N}$. We will not use the commutator subgroup in future results in this book, so for us it is merely a curiosity.

Equivalence Relations on Groups

Why are normal subgroups important? In the preliminary chapter we discussed equivalence relations and the associated set of equivalence classes. If $G$ is a group and $\sim$ is an equivalence relation, when does $G/\sim$ admit a group structure? Of course we have to specify the multiplication on $G/\sim$. We will do so now.

Definition 10: Let $G$ be a group and $\sim$ is an equivalence relation on $G$, we define multiplication on the equivalence classes in $G/\sim$ such that for all $a,b\in G$,

$[a][b]=[ab]$

This is indeed the only natural way to do it. Take the two equivalence classes, choose representatives, compute their product and take its equivalence class. The alert reader will have only one thing on his/her mind: is this well defined? For a general equivalence relation, the answer is no. The reader is invited to come up with an example. What is more interesting is when is it well defined? By the definition above, we obviously need the projection map $\pi \,:\,G\rightarrow G/\sim$ defined by $a\mapsto [a]$ to be a homomorphism. We can in fact condense the requirements down to two, both having to do with cancellation laws.

Theorem 11: Let $G$ be a group and $\sim$ an equivalence relation on $G$. Then $G/\sim$ is a group under the natural multiplication if and only if for all $a,b,g\in G$

$a\sim b\,\Leftrightarrow ag\sim bg\wedge ga\sim gb$.

Proof: Assume $G/\sim$ is a group. Since $a\sim b\,\Leftrightarrow [a]=[b]$, the property follows from the cancellation laws in $G$. Assume now that the property holds. Then its multiplication rule is well defined, and must verify that $G/\sim$ is a group. Let $a,b,c\in G$, then associativity is inherited from $G$:

$([a][b])[c]=[ab][c]=[(ab)c]=[a(bc)]=[a][bc]=[a]([b][c])$.

The identity in $G/\sim$ is the equivalence class of $e\in G$, $[e]$:

$[e][a]=[ea]=[a]=[ae]=[a][e]$.

Finally, the inverse of $[a]$ is $[a^{-1}]$:

$[g][g^{-1}]=[gg^{-1}]=[e]=[g^{-1}g]=[g^{-1}][g]$.

So $G/\sim$ really defines a group structure, proving the theorem. ∎

We will call an equivalence relation $\sim$ compatible with $G$ if $G/\sim$ is a group. Then, $G/\sim$ is called the quotient group of $G$ by $\sim$. Also, as an immediate consequence, this makes $\pi \,:\,G\rightarrow G/\sim$ into a homomorphism, but not just any homomorphism! It satisfies a universal property!

Commutative diagram showing the universal property satisfied by the projection homomorphism.

Theorem 12: Let $\sim$ be en equivalence relation compatible with $G$, and $\phi \,:\,G\rightarrow H$ a group homomorphism such that $a\sim b\,\Rightarrow \,\phi (a)=\phi (b)$. Then there exists a unique homomorphism ${\tilde {\phi }}\,:\,G/\sim \rightarrow H$ such that $\phi ={\tilde {\phi }}\circ \pi$.

Proof: In the preliminary chapter on set theory, we showed the corresponding statement for sets, so we know that ${\tilde {\phi }}$ exists as a function between sets. We have to show that it is a homomorphism. This follows immediately: since ${\tilde {\phi }}([a])=\phi (a)$ by commutativity, we have ${\tilde {\phi }}([a]){\tilde {\phi }}([b])=\phi (a)\phi (b)=\phi (ab)={\tilde {\phi }}([ab])={\tilde {\phi }}([a][b])$. As stated already, ${\tilde {\phi }}([a])=\phi (a)$ shows uniqueness, proving the theorem. ∎

Lemma 13: Let $\sim$ be an equivalence relation on a group $G$ such that $a\sim b\,\Leftrightarrow ga\sim gb$. Then $H=[e]$ is a subgroup of $G$ and $a\sim b\,\Leftrightarrow \,a^{-1}b\in H\,\Leftrightarrow \,aH=bH$.

Proof: First off, $H$ is nonempty since $e\in H$. Let $a,b\in H$. Then $b\sim e\,\Leftrightarrow \,e\sim b^{-1}$ by multiplying on the left by $b^{-1}$. Then since $e\sim a$ we have $a^{-1}\sim e$ by the same argument. Applying transitivity gives $a^{-1}\sim b^{-1}$. Finally, multiplying on the left by $a$ gives $e\sim ab^{-1}$, giving $ab^{-1}\in H$ and so $H=[e]$ is a subgroup.

Assume $a\sim b$ for $a,b\in G$. Then $[a]=[b]$ implying $[a^{-1}b]=[e]$. Thus $a^{-1}b\in [e]$. Now assume $a^{-1}b\in [e]$. Then $[a^{-1}b]=[e]$ and so $[a]=[b]$ and finally $a\sim b$.

Assume $a^{-1}b\in H$. Then since $H$ is a subgroup, we have $a^{-1}bH=H$ and so $aH=bH$. Finally, assume $aH=bH$. Then $a^{-1}bH=H$. Since in particular $e\in H$, this implies $a^{-1}b\in H$, completing the proof. ∎

The mirror version using right cosets and the equivalence relation $a\sim b\,\Leftrightarrow ag\sim bg$ and $a\sim b\,\Leftrightarrow \,ab^{-1}\in H\,\Leftrightarrow \,Ha=Hb$ is completely analogous. Stating the theorem and writing out the proof is left to the reader as an exercise.

We have showed how an equivalence relation defines a subgroup of $G$. In fact the equivalence classes are all cosets of this subgroup. We will now go the other way, and show how a subgroup defines an equivalence relation on $G$.

Lemma 14: Let $H$ be a subgroup of a group $G$. Then,

i) $a\sim _{L}b\,\Leftrightarrow \,a^{-1}b\in H\,\Leftrightarrow \,aH=bH$ is an equivalence relation such that $a\sim _{L}b\,\Leftrightarrow \,ga\sim _{L}gb$ for all $g\in G$.

ii) $a\sim _{R}b\,\Leftrightarrow \,ab^{-1}\in H\,\Leftrightarrow \,Ha=Hb$ is an equivalence relation such that $a\sim _{R}b\,\Leftrightarrow \,ag\sim _{R}bg$ for all $g\in G$.

Proof: We will prove i). The proof for ii) is similar and is left as an exercise for the reader.

The fact that $\sim$ is an equivalence relation and that $a^{-1}b\in H\,\Leftrightarrow \,aH=bH$ was proven in the section on subgroups. Assume $a\sim _{L}b$. Then for all $g\in G$, $(ga)^{-1}(gb)=a^{-1}g^{-1}gb=a^{-1}b\in H$ such that $ga\sim _{L}gb$. Now assume $ga\sim _{L}gb$, Then $a^{-1}b=a^{-1}g^{-1}gb=(ga)^{-1}(gb)\in H$ such that $a\sim _{L}b$, completing the proof. ∎

Theorem 15: For every equivalence relation $\sim _{L}$ on G such that $a\sim _{L}b\,\Leftrightarrow ga\sim _{L}gb$, there exists a unique subgroup $H$ of $G$ such that $G/\sim$ are precisely the left cosets of $H$.

Proof: This follows from Lemma 13 and Lemma 14.

Again, the mirror statement is completely analogous. Stating the theorem is left to the reader as an exercise.

Quotients with respect to Normal Subgroups

Lemma 16: Let $\sim _{L}$ be the equivalence relation given by $a\sim _{L}b:\Leftrightarrow aH=bH$, where $H$ is a subgroup of G. Then we know that $\sim _{L}$ is compatible if and only if $H$ is a normal subgroup.

Proof: Assume $\sim _{L}$ is compatible, $g\in G$ and $a\in H$. Then $a\sim _{L}e$, and compatibility gives us $gag^{-1}\sim _{L}gg^{-1}=e$, and so $gag^{-1}\in H$. Since $a$ is arbitrary, we obtain $gHg^{-1}=H$ for all $g\in G$ and so $H$ is normal. Assume now that $H$ is normal. Then $aH=bH\,\Leftrightarrow a^{-1}b\in H$, $Ha=Hb\,\Leftrightarrow ab^{-1}\in H$ and $aH=Ha$ for all $a,b\in G$. Using this, we obtain $a\sim _{L}b\,\Leftrightarrow ab^{-1}=ab^{-1}bg(bg)^{-1}\sim _{L}e\,\Leftrightarrow ab^{-1}bg=ag\sim _{L}bg$ and similarly for the right hand case, so $\sim _{L}$ is compatible with $G$. ∎

Definition 17: When an equivalence relation is given by specifying a normal subgroup $H$, the quotient group with respect to this equivalence relation is denoted $G/H$. We then refer to $G/H$ as the quotient of $G$ with respect to $H$, or $G$ modulo $H$. Note that this complies with previous definitions of this notation.

Multiplication in $G/H$ is given as before as $(aH)(bH)=(ab)H$, with identity $H$ and $(aH)^{-1}=a^{-1}H$ for all $a,b\in G$.

Definition 18: Let $H$ be a normal subgroup of $G$. Then we define the projection homomorphism $\pi \,:\,G\rightarrow G/H$ by $\pi (a)=aH$ for all $a\in G$.

Theorem 19: A subgroup is normal if and only if it is the kernel of some homomorphism.

Proof: We have already covered the left implication. For the right implication, assume $H$ is normal. Then $G/H$ is a group and we have the projection homomorphism $\pi \,:\,G\rightarrow G/H$ as defined above. Since for all $h\in H$ we have $\pi (h)=hH=H$, $\ker \,\pi =H$ and so $H$ is the kernel of a homomorphism. ∎

Theorem 20: Let $G,G^{\prime }$ be groups, $\phi \,:\,G\rightarrow G^{\prime }$ a homomorphism and $H$ a normal subgroup of $G$ such that $H\subseteq \ker \,\phi$. Then there exists a unique homomorphism ${\tilde {\phi }}\,:\,G/H\rightarrow G^{\prime }$ such that ${\tilde {\phi }}\circ \pi =\phi$.

Proof: This follows from Theorem 12 by letting $a\sim b\,\Leftrightarrow aH=bH$. ∎

The Isomorphism Theorems

Commutative diagram showing the first isomorphism theorem. ${\tilde {\phi }}$ is an isomorphism.

Theorem 21 (First Isomorphism Theorem): Let $G,G^{\prime }$ be groups and $\phi \,:\,G\rightarrow G^{\prime }$ a homomorphism. Then $G/\ker \,\phi \approx \mathrm {im} \,\phi$.

Proof: From Theorem 20 we have that there exists a unique homomorphism ${\tilde {\phi }}\,:\,G/\ker \,\phi \rightarrow G^{\prime }$ such that $\phi ={\tilde {\phi }}\circ \pi$. We have to show that ${\tilde {\phi }}$ is an isomorphism when we corestrict to $\mathrm {im} \,\phi$. This is immediate, since $\phi (a)=\phi (b)\,\Leftrightarrow a\ker \phi =b\ker \phi$ by Lemma 13, so that ${\tilde {\phi }}$ is injective, and for any $g^{\prime }\in \mathrm {im} \,\phi$ there is a $g\in G$ such that $\phi (g)={\tilde {\phi }}(g\ker \,\phi )=g^{\prime }$ so that it is surjective and therefore an isomorphism. ∎

Lemma 22: Let $G$ be a group, $H$ a subgroup and $K$ a normal subgroup of $G$. Then $H\cap K$ is a normal subgroup of $H$.

Proof: Let $h\in H$ and $k\in H\cap K$. Then $hkh^{-1}\in H$ since $h,k\in H$ and $H$ is a subgroup and $hkh^{-1}\in K$ since $k\in K$, $h\in G$ and $K$ is normal in $G$. Thus $hkh^{-1}\in H\cap K$ and $H\cap K$ is normal in $H$. ∎

Theorem 23 (Second Isomorphism Theorem): Let $G$ be a group, $H$ a subgroup and $K$ a normal subgroup of $G$. Then $HK/K\approx {\frac {H}{H\cap K}}$.

Proof: Define $\phi \,:\,H\rightarrow HK/K$ by $\phi (h)=hK$ for all $h\in H$. $\phi$ is surjective since any element in $HK$ can be written as $hk$ with $h\in H$ and $k\in K$, so $\phi (h)=\pi (hk)=hkK=hK$. We also have that $\ker \,\phi =\{h\in H\mid hK=K\}=\{h\in H\mid h\in K\}=H\cap K$ and so $HK/K\approx {\frac {H}{H\cap K}}$ by the first isomorphism theorem. ∎

Lemma 24: Let $G$ be a group, and let $H,K$ be normal subgroups of $G$ such that $K\subseteq H\subseteq G$. Then $H/K$ is a normal subgroup of $G/K$.

Proof: Let $h\in H$ and $g\in G$. Then $ghg^{-1}=h^{\prime }$ for some $h^{\prime }\in H$ since $H$ is normal. Thus $(gK)(hK)(gK)^{-1}=(ghg^{-1})K=h^{\prime }K$, showing that $H/K$ is normal in $G/K$. ∎

Theorem 25 (Third Isomorphism Theorem) Let $G$ be a group, and let $H,K$ be normal subgroups of $G$ such that $K\subseteq H\subseteq G$. Then ${\frac {G/K}{H/K}}\approx G/H$.

Proof: Let $\phi \,:\,G/K\rightarrow G/H$ be given by $\phi (gK)=gH$. This is well defined and surjective since $K\subseteq H$, and is a homomorphism. Its kernel is given by $\ker \,\phi =\{gK\in G/K\mid gH=H\}=\{gK\in G/K\mid g\in H\}=H/K$, so by the first isomorphism theorem, ${\frac {G/K}{H/K}}\approx G/H$. ∎

Theorem 26 (The Correspondence Theorem): Let $G$ be a group and $K$ be a normal subgroup. Now let $A=\{H\leq G\mid K\leq H\}$ and $B=\{H^{\prime }\mid H^{\prime }\leq G/K\}$. Then $\pi \,:\,H\mapsto \pi (H)$ is an order-preserving bijection from $A$ to $B$.

Proof: We must show injectivity and surjectivity. For injectivity, note that if $K\leq H$, then $\pi ^{-1}(\pi (H))=HK=H$, so if $H_{1},H_{2}\in A$ such that $\pi (H_{1})=\pi (H_{2})$, then $H_{1}=\pi ^{-1}(\pi (H_{1}))=\pi ^{-1}(\pi (H_{2}))=H_{2}$, proving injectivity. For surjectivity, let $H^{\prime }\in B$. Then $K\leq \pi ^{-1}(H^{\prime })\leq G$, so that $\pi ^{-1}(H^{\prime })\in A$, and $\pi (\pi ^{-1}(H^{\prime }))=H^{\prime }$, proving surjectivity. Lastly, since $H_{1}\subseteq H_{2}$ implies that $\pi (H_{1})\subseteq \pi (H_{2})$, the bijection is order-preserving. ∎

Note 27: The correspondence Theorem is sometimes called The Forth Isomorphism Theorem.

Theorem 28: Let $H\in A$ from Theorem 26. Then $H$ is normal if and only if $\pi (H)$ is normal in $G/K$, and then $G/H\approx {\frac {G/K}{\pi (H)}}$.

Proof: Since $\pi$ is surjective, $H$ normal implies $\pi (H)$ normal. Assume that $\pi (H)$ is normal. Then $\pi ^{-1}(\pi (H))=H$ and so $H$ is normal since it is the preimage of a normal subgroup. To show the isomorphism, let $\phi \,:\,G\rightarrow {\frac {G/K}{\pi (H)}}$ be given by a composition of projections: $\phi \,:\,\pi _{\pi (H)}\circ \pi _{K}$. Then $\ker \,\phi =\{g\in G\mid \phi (g)=\pi (H)\}=\{g\in G\mid \pi (g)\in \pi (H)\}=\pi ^{-1}(\pi (H))=H$, so by the first isomorphism teorem, $G/H\approx {\frac {G/K}{\pi (H)}}$. ∎

Corollary 29: Let $G$ be a group and $H$ a normal subgroup. Then for any $K^{\prime }\leq G/H$ there exists a unique subgroup $K\leq G$ such that $H\leq K\leq G$ and $K=K^{\prime }H$. Also, $K$ is normal in $G$ if and only if $K^{\prime }$ is normal in $G/H$.

Proof: From Theorem 26 we have that the projection $K\mapsto \pi (K)=K^{\prime }$ is a bijection, and since $\pi (g)=gH$ for all $g\in G$, we have $K=K^{\prime }H$. The second part follows from Theorem 28. ∎

Theorem 2.6.? (Baumslag):

Let $G$ be a group, let $K,H$ be subgroups of $G$ such that $K\trianglelefteq H$, and let $I$ be a subgroup of $G$ such that $\forall h\in H:hI=Ih$. Then:

$HI/KI\cong H/(K(H\cap I))$

Proof:

Due to theorem 2.6.?, $HI$ and $KI$ are subgroups of $G$. Further, theorem 2.6.? implies that $KI\trianglelefteq HI$. Therefore, the function

$\Phi :H\to HI/KI,\Phi (h):=hKI$

is a homomorphism.

Further, since $K$ is a subgroup of $H$, for all $h=\kappa \iota \in KI,\kappa \in K,\iota \in I$ we have:

$h\in H\Rightarrow \kappa ^{-1}h=\iota \in H$

And thus:

${\begin{aligned}h\in \ker \Phi &\Leftrightarrow h=\kappa \iota ,\kappa \in K,\iota \in I\\&\Leftrightarrow h=\kappa \iota ,\kappa \in K,\iota \in H\cap I\\&\Leftrightarrow h\in K(H\cap I)\end{aligned}}$

Therefore, $\ker \Phi =K(H\cap I)$. Thus, the first isomorphism theorem implies

$HI/KI\cong H/(K(H\cap I))$ $\Box$

Simple Groups

Definition 30: A group is called simple if it has no non-trivial proper normal subgroups.

Example 31: Every cyclic group $\mathbb {Z} _{p}$, where $p$ is prime, is simple.

Definition 32: Let $G$ be a group and $H$ a normal subgroup. $H$ is called a maximal normal subgroup if for any normal subgroup $K$ of $G$, we have $K\subseteq H$.

Theorem 33: Let $G$ be a group and $H$ a normal subgroup. Then $H$ is a maximal normal subgroup if and only if the quotient $G/H$ is simple.

Proof: By Theorem 26 and Theorem 28, $G/H$ has a nontrivial normal subgroup if and only if there exists a proper normal subgroup $K$ of $G$ such that $H\leq K\leq G$. That is, $H$ is not maximal if and only if $G/H$ is not simple. The theorem follows. ∎

Problems

Problem 1: Recall the unitary and special unitary groups from the section about subgroups. Define the projective unitary group of order $n$ as the group $PU(n)=U(n)/Z(U(n))$. Similarly, define the projective special unitary group of order $n$ as $PSU(n)=SU(n)/Z(SU(n))$.

i) Show that $Z(SU(n))=SU(n)\cap Z(U(n)\approx \mathbb {Z} _{n}$

ii) Using the second isomorphism theorem, show that $PSU(n)\approx PU(n)$.

Group Theory/Products and Free Groups

During the preliminary sections we introduced two important constructions on sets: the direct product and the disjoint union. In this section we will construct the analogous constructions for groups.

Product Groups

Definition 1: Let $G$ and $H$ be groups. Then we can define a group structure on the direct product $G\times H$ of the sets $G$ and $H$ as follows. Let $(g_{1},h_{1}),(g_{2},h_{2})\in G\times H$. Then we define the multiplication componentwise: $(g_{1},h_{1})(g_{2},h_{2})=(g_{1}g_{2},h_{1}h_{2})$. This structure is called the direct product of $G$ and $H$.

Remark 2: The product group is a group, with identity $(e_{G},e_{H})$ and inverses $(g,h)^{-1}=(g^{-1},h^{-1})$. The order of $G\times H$ is $|G\times H|=|G||H|$.

Theorem 3: Let $G$ and $H$ be groups. Then we have homomorphisms $\pi _{1}\,:\,G\times H\rightarrow G$ and $\pi _{2}\,:\,G\times H\rightarrow H$ such that $\pi _{1}(g,h)=g$ and $\pi _{2}(g,h)=h$ for all $(g,h)\in G\times H$. These are called the projections on the first and second factor, respectively.

Proof: The projections are obviously homomorphisms since they are the identity on one factor and the trivial homomorphism on the other. ∎

Corollary 4: Let $G$ and $H$ be groups. Then ${\frac {G\times H}{H}}\approx G$ and ${\frac {G\times H}{G}}\approx H$.

Proof: This follows immediately from plying the first isomorphism theorem to Theorem 3 and using that $G\times \{e_{H}\}\approx G$ and $\{e_{G}\}\times H\approx H$. ∎

Theorem 5: Let $G$ and $H$ be groups. Then $G\times \{e_{H}\}$ and $\{e_{G}\}\times H$ are normal subgroups of $G\times H$.

Proof: We prove the theorem for $G\times \{e_{H}\}$. The case for $\{e_{G}\}\times H$ is similar. Let $g,g^{\prime }\in G$ and $h\in H$. Then $(g,h)(g^{\prime },e_{H})(g,h)^{-1}=(gg^{\prime }g^{-1},hh^{-1})=(gg^{\prime }g^{-1},e_{H})\in G\times \{e_{H}\}$. ∎

Commutative diagram showing the universal property satisfied by the direct product.

We stated that this is an analogous construction to the direct product of sets. By that we mean that it satiesfies the same universal property as the direct product. Indeed, to be called a "product", a construction should have to satisfy this universal property.

Theorem 6: Let $G$ and $H$ be groups. Then if $K$ is a group with homomorphisms $\phi _{1}\,:\,K\rightarrow G$ and $\phi _{2}\,:\,K\rightarrow H$, then there exists a unique homomorphism $u\,:\,K\rightarrow G\times H$ such that $\phi _{1}=\pi _{1}\circ u$ and $\phi _{2}=\pi _{2}\circ u$.

Proof: By the construction of the direct product, $u\,:\,K\rightarrow G\times H$ is a homomorphism if and only if $\pi _{1}\circ u$ and $\pi _{2}\circ u$ are homomorphisms. Thus $u\,:\,K\rightarrow G\times H$ defined by $u((g,h))=(\phi _{1}(g),\phi _{2}(h))$ is one homomorphism satisfying the theorem, proving existence. By the commutativity condition this is the only such homomorphism, proving uniqueness. ∎

Products of Cyclic Groups

Theorem 7: The order of an element $(a,b)\in \mathbb {Z} _{m}\times \mathbb {Z} _{n}$ is $|(a,b)|=\mathrm {lcm} (|a|,|b|)$.

Proof: The lowest positive number $c$ such that $(a,b)^{c}=(ac,bc)=(0,0)$ is the smallest number such that $ac=rm$ and $bc=sn$ for integers $r,s$. It follows that $c$ divides both $|a|$ and $|b|$ and is the smallest such number. This is the definition of the least common divider. ∎

Theorem 8: $\mathbb {Z} _{m}\times \mathbb {Z} _{n}$ is isomorphic to $\mathbb {Z} _{mn}$ if and only if $m$ and $n$ are relatively prime.

Proof: We begin with the left implication. Assume $\mathbb {Z} _{m}\times \mathbb {Z} _{n}\approx \mathbb {Z} _{mn}$. Then $\mathbb {Z} _{m}\times \mathbb {Z} _{n}$ is cyclic, and so there must exist an element with order $mn$. By Theorem 7 we there must then exist a generator $(a,b)\neq (0,0)$ in $\mathbb {Z} _{m}\times \mathbb {Z} _{n}$ such that $\mathrm {lcm} (|a|,|b|)=mn$. Since each factor of the generator must generate its group, this implies $\mathrm {lcm} (m,n)=mn$, and so $\gcd(m,n)=1$, meaning that $m$ and $n$ are relatively prime. Now assume that $m$ and $n$ are relatively prime and that we have generators $a$ of $\mathbb {Z} _{m}$ and $b$ of $\mathbb {Z} _{n}$. Then since $\gcd(m,n)=1$, we have $\mathrm {lcm} (m,n)=mn$ and so $|(a,b)|=mn$. this implies that $(a,b)$ generates $\mathbb {Z} _{m}\times \mathbb {Z} _{n}$, which must then be isomorphic to a cyclic group of order $mn$, im particular $\mathbb {Z} _{mn}$. ∎

Theorem 9 (Characterization of finite abelian groups): Let $G$ be an abelian group. Then there exists prime numbers $p_{1},...,p_{n}$ and positive integers $r_{1},...,r_{n}$, unique up to order, such that

$G\approx \mathbb {Z} _{p_{1}^{r_{1}}}\times ...\times \mathbb {Z} _{p_{n}^{r_{n}}}$

Proof: A proof of this theorem is currenly beyond our reach. However, we will address it during the chapter on modules. ∎

Subdirect Products and Fibered Products

Definition 10: A subdirect product of two groups $G$ and $H$ is a proper subgroup $K$ of $G\times H$ such that the projection homomorphisms are surjective. That is, $\pi _{1}(K)=G$ and $\pi _{2}(K)=H$.

Example 11: Let $G$ be a group. Then the diagonal $\Delta =\{(g,g)\mid g\in G\}\subseteq G\times G$ is a subdirect product of $G$ with itself.

Definition 12: Let $G$, $H$ and $Q$ be groups, and let the homomorphisms $\phi \,:\,G\rightarrow Q$ and $\psi \,:\,H\rightarrow Q$ be epimorphisms. The fiber product of $G$ and $H$ over $Q$, denoted $G\times _{Q}H$, is the subgroup of $G\times H$ given by $G\times _{Q}H=\{(g,h)\in G\times H\mid \phi (g)=\psi (h)\}$.

In this subsection, we will prove the equivalence between subdirect products and fiber products. Specifically, every subdirect product is a fiber product and vice versa. For this we need Goursat's lemma.

Theorem 13 (Goursat's lemma): Let $G$ and $G^{\prime }$ be groups, and $H\subseteq G\times G^{\prime }$ a subdirect product of $G$ and $G^{\prime }$. Now let $N=\ker \,\pi _{2}$ and $N^{\prime }=\ker \,\pi _{1}$. Then $N$ can be identified with a normal subgroup of $G$, and $N^{\prime }$ with a normal subgroup of $G^{\prime }$, and the image of $H$ when projecting on $G/N\times G^{\prime }/N^{\prime }$ is the graph of an isomorphism $G/N\approx G^{\prime }/N^{\prime }$.

Proof:

Further reading

More on the automorphism groups of finite abelian groups. Some results require theory of group actions and ring theory, which is developed in a later section.

http://arxiv.org/pdf/math/0605185v1.pdf

Free Groups

In order to properly define the free group, and thereafter the free product, we need some preliminary definitions.

Definition 10: Let $A$ be a set. Then a word of elements in $A$ is a finite sequence $a_{1}a_{2}...a_{n}$ of elements of $A$, where the positive integer $n$ is the word length.

Definition 11: Let $x=a_{1}...a_{n}$ and $y=a_{n+1}...a_{n+k}$ be two words of elements in $A$. Define the concatenation of the two words as the word $xy=a_{1}...a_{n}a_{n+1}...a_{n+k}$.

Now, we want to make a group consisting of the words of a given set $A$, and we want this group to be the most general group of this kind. However, if we are to use the concatenation operation, which is the only obvious operation on two words, we are immediately faced with a problem. Namely, deciding when two words are equal. According to the above, the length of a product is the sum of the lengths of the factors. In other words, the length cannot decrease. Thus, a word of length $n$ multiplied with its inverse has length at least $n$, while the identity word, which is the empty word, has length $0$. The solution is an algorithm to reduce words into irreducible ones. These terms are defined below.

Definition 12: Let $A$ be any set. Define the set $W(A)$ as the set of words of powers of elements of $A$. That is, if $a_{1},...,a_{n}\in A$ and $r_{1},...,r_{n}\in \mathbb {Z}$, then $a_{1}^{r_{1}}...a_{n}^{r_{n}}\in W(A)$.

Definition 13: Let $x=a_{1}^{r_{1}}...a_{n}^{r_{n}}\in W(A)$. Then we define a reduction of $x$ as follows. Scan the word from the left until the first pair of indices $j,j+1$ such that $a_{j}=a_{j+1}$ is encountered, if such a pair exists. Then replace $a_{j}^{r_{j}}a_{j+1}^{r_{j+1}}$ with $a_{j}^{r_{j}+r_{j+1}}$. Thus, the resulting word is $x_{(1)}=a_{1}^{r_{1}}...a_{j-1}^{r_{j-1}}a_{j}^{r_{j}+r_{j+1}}a_{j+2}^{r_{j+2}}...a_{n}^{r_{n}}$. If no such pair exists, then $x=x_{(1)}$ and the word is called irreducible.

It should be obvious if $x\in W(A)$ with length $n$, then $x_{(n)}$ will be irreducible. The details of the proof is left to the reader.

Definition 14: Define the free group $F(A)$ on a set $A$ as follows. For each word $x\in W(A)$ of length $n$, let the reduced word $x_{(n)}\in F(A)$. Thus $F(A)\subseteq W(A)$ is the subset of irreducible words. As for the binary operation on $F(A)$, if $x,y\in F(A)$ have lengths $n$ and $m$ respectively, define $x*y$ as the completely reduced concatenation $(xy)_{(n+m)}$.

Theorem 15: $F(A)$ is a group.

Proof:

Example 16: We will concider free groups on 1 and 2 letters. Let $A_{1}=\{a\}$ and $A_{2}=\{a,b\}$. Then

$F(A_{1})=\{a^{n}\mid n\in \mathbb {Z} \}$ with $a^{n}a^{m}=a^{n+m}$.

$F(A_{2})=\{\prod _{i=1}^{n}a_{i}b_{i}\mid a_{i}\in F(\{a\}),b_{i}\in F(\{b\})\}$ such that $a_{i}\neq e$ for any $i>1$ and $b_{i}\neq e$ for any $i<n$. Example product: $(a^{2}b^{-3}a)(a^{-1}ba)=a^{2}b^{-3}aa^{-1}ba=a^{2}b^{-3}ba=a^{2}b^{-2}a$.

Group Presentations

In this subsection we will briefly introduce another method used for defining groups. This is by prescribing a group presentation.

Definition 17: Let $G$ be a group and $H$ a subgroup. Then define the normal closure of $H$ in $G$ as the intersection of all normal subgroups in $G$ containing H. That is, if $N$ is the normal closure of $H$, then

$N=\bigcap _{\stackrel {K\trianglelefteq G}{H\subseteq K}}K$.

Definition 18: Let $S$ be a set and $R\subseteq F(S)$. Let $N$ be the normal closure of $R$ in $F(S)$ and define the group $\langle S\mid R\rangle =F(S)/N$. The elements of $S$ are called generators and the elements of $R$ are called relators. If $G$ is a group such that $G\approx \langle S\mid R\rangle$, then $\langle S\mid R\rangle$ is said to be a presentation of $G$.

The Free Product

Using the previously defined notion of a group presentation, we can now define another type of group product.

Definition : Let $G$ and $G^{\prime }$ be groups with presentations $\langle S\mid R\rangle$ and $\langle S^{\prime }\mid R^{\prime }\rangle$. Define the free product of $G$ and $G^{\prime }$, denoted $G*G^{\prime }$, as the group with the presentation $\langle S\cup S^{\prime }\mid R\cup R^{\prime }\rangle$.

Remark : Depending on the context, spesifically if we only deal with abelian groups, we may require the free product of abelian groups to be abelian. In that case, the free product equals the direct product. This is another example of abelian groups being better behaved than nonabelian groups.

Lemma : The free product includes the component groups as subgroups.

Remark : The free product is not a product in the sense discussed previously. It does not satifsy the universal property other products do. Instead, it satisfies the "opposide", or dual property, obtained by reversing the direction of all the arrows in the commutative diagram. We usually call a construction satisfying this universal property a coproduct.

Problems

Problem 1: Let $H$ and $K$ be groups of relatively prime orders. Show that any subgroup of $H\times K$ is the product of a subgroup of $H$ with a subgroup of $K$.

Answer

Coming soon. ∎

Group Theory/Group actions on sets

Interesting in it's own right, group actions are a useful tool in algebra and will permit us to prove the Sylow theorems, which in turn will give us a toolkit to describe certain groups in greater detail.

Basics

Definition 1.8.1:

Let $X$ be an arbitrary set, and let $G$ be a group. A function

$f:G\times X\to X$

is called group action by $G$ on $X$ if and only if ($\iota$ denoting the identity of $G$)

1. $\forall x\in X:f(\iota ,x)=x$ and
2. $\forall \sigma ,\tau \in G,x\in X:f(\sigma ,f(\tau ,x))=f(\sigma \tau ,x)$.

When a certain group action is given in a context, we follow the prevalent convention to write simply $\sigma x$ for $f(\sigma ,x)$. In this notation, the requirements for a group action translate into

1. $\forall x\in X:\iota x=x$ and
2. $\forall \sigma ,\tau \in G,x\in X:\sigma (\tau x)=(\sigma \tau )x$.

There is a one-to-one correspondence between group actions of $G$ on $X$ and homomorphisms $G\to S_{X}$.

Definition 1.8.2:

Let $G$ be a group and $X$ a set. Given a homomorphism $\varphi :G\to S_{X}$, we may define a corresponding group action by

$\sigma x:=\varphi (\sigma )(x)$.

If we are given a group action $G\times X\to X$, then

$\varphi (\sigma ):=x\mapsto \sigma x$

is a homomorphism. The thus defined correspondence between homomorphisms $G\to S_{X}$ and group actions $G\times X\to X$ is a bijective one.

Proof:

1.

Indeed, if $\varphi :G\to S_{X}$ is a homomorphism, then

$\iota x=\varphi (\iota )(x)={\text{Id}}(x)=x$ and

$\sigma (\tau x)=\varphi (\sigma )(\varphi (\tau )(x))=(\varphi (\sigma )\circ \varphi (\tau ))(x)=(\sigma \tau )(x)$.

2.

$\varphi (\sigma )$ is bijective for all $\sigma \in G$, since

$\varphi (\sigma )(x)=\varphi (\sigma )(y)\Leftrightarrow \sigma x=\sigma y\Leftrightarrow \sigma ^{-1}\sigma x=\sigma ^{-1}\sigma y$.

Let also $\tau \in G$. Then

$\varphi (\sigma \tau )=x\mapsto (\sigma \tau )x=x\mapsto \sigma (\tau (x))=(x\mapsto \sigma x)\circ (x\mapsto \tau x)=\varphi (\sigma )\circ \varphi (\tau )$.

3.

We note that the constructions treated here are inverse to each other; indeed, if we transform a homomorphism $\varphi :G\to S_{X}$ to an action via

$\sigma x:=\varphi (\sigma )(x)$

and then turn this into a homomorphism via

$\psi :G\to S_{X},\psi (\sigma ):=x\mapsto \sigma x$,

we note that $\psi =\phi$ since $\psi (\sigma )=x\mapsto \sigma x=x\mapsto \varphi (\sigma )(x)=\varphi (\sigma )$.

On the other hand, if we start with a group action $G\times X\to X$, turn that into a homomorphism

$\varphi (\sigma ):=x\mapsto \sigma x$

and turn that back into a group action

$\sigma x:=\varphi (\sigma )(x)$,

then we ended up with the same group action as in the beginning due to $\varphi (\sigma )(x)=\sigma x$.$\Box$

Examples 1.8.3:

1. $S_{n}$ acts on $\mathbb {R} ^{n}$ via $\sigma (x_{1},\ldots ,x_{n})=(x_{\sigma (1)},\ldots ,x_{\sigma (n)})$.
2. $GL_{n}(\mathbb {R} )$ acts on $\mathbb {R} ^{n}$ via matrix multiplication: $Ax:=Ax$, where the first juxtaposition stands for the group action definition and the second for matrix multiplication.

Types of actions

Definitions 1.8.4:

A group action $G\times X\to X$ is called

1. faithful iff $(\forall x\in X:\sigma x=\tau x)\Rightarrow \sigma =\tau$ ('identity on all elements of $x$ enforces identity on $G$')
2. free iff $(\exists x\in X:\sigma x=\tau x)\Rightarrow \sigma =\tau$ ('different group elements map an $x$ to different elements of $X$'), and
3. transitive iff for all $x,y\in X$ there exists $\sigma \in G$ such that $y=\sigma x$.

Subtle analogies to real life become apparent if we note that an action is faithful if and only if for two distinct $\sigma \neq \tau \in G$ there exist $x\in X$ such that $\sigma x\neq \tau x$, and it is free if and only if the elements $\sigma x,\sigma \in G$ are all different for all $x\in X$.

Theorem 1.8.5:

A free operation on a nonempty set is faithful.

Proof: $(\forall x\in X:\sigma x=\tau x)\Rightarrow (\exists x\in X:\sigma x=\tau x)\Rightarrow \sigma =\tau$.$\Box$

We now attempt to characterise these three definitions; i.e. we try to find conditions equivalent to each.

Theorem 1.8.6:

A group action $G\times X\to X$ is faithful if and only if the induced homomorphism $\varphi :G\to S_{X}$ is injective.

Proof:

Let first a faithful action $G\times X\to X$ be given. Assume $\varphi (\sigma )=\varphi (\tau )$. Then for all $x\in X$ $\sigma x=\varphi (\sigma )(x)=\varphi (\tau )(x)=\tau x$ and hence $\sigma =\tau$. Let now $\varphi$ be injective. Then ${\displaystyle }$.

An important consequence is the following

Corollary 1.8.7 (Cayley):

Every group is isomorphic to some subgroup of a symmetric group.

Proof:

A group acts on itself faithfully via left multiplication. Hence, by the previous theorem, there is a monomorphism $G\to S_{G}$.$\Box$

For the characterisation of the other two definitions, we need more terminology.

Orbit and stabilizer

Definitions 1.8.8:

Let $G\times X\to X$ be a group action, and let $x\in X$. Then

• $G(x):=\{\sigma x|\sigma \in G\}$ is called the orbit of $x$ and
• $G_{x}:=\{\sigma \in G|\sigma x=x\}$ is called the stabilizer of $x$. More generally, for a subset $Y\subseteq X$ we define $G_{Y}:=\{\sigma \in G|\forall y\in Y:\sigma y\in Y\}$ as the stabilizer of $Y$.

Using this terminology, we obtain a new characterisation of free operations.

Theorem 1.8.9:

An operation $G\times X\to X$ is free if and only if $G_{x}$ is trivial for each $x\in X$.

Proof: Let the operation be free and let $x\in X$. Then

$\sigma \in G_{x}\Leftrightarrow \sigma x=x=\iota x$.

Since the operation is free, $\sigma =\iota$.

Assume that for each $x\in X$, $G_{x}$ is trivial, and let $y\in X$ such that $\sigma y=\tau y$. The latter is equivalent to $\tau ^{-1}\sigma y=y$. Hence $\tau ^{-1}\sigma \in G_{y}=\{\iota \}$.$\Box$

We also have a new characterisation of transitive operations using the orbit:

Theorem 1.8.10:

An operation $G\times X\to X$ is transitive if and only if for all $x\in X$ $G(x)=X$.

Proof:

Assume for all $x\in X$ $G(x)=X$, and let $y,z\in X$. Since $G(y)=X\ni z$ transitivity follows.

Assume transitivity, and let $x\in X$. Then for all $y\in X$ there exists $\sigma \in G$ with $\sigma x=y$ and hence $y\in G(x)$.$\Box$

Regarding the stabilizers we have the following two theorems:

Theorem 1.8.11:

Let $G\times X\to X$ be a group action and $x\in X$. Then $G_{x}\leq G$.

Proof:

First of all, $\iota \in G_{x}$. Let $\sigma ,\tau \in G_{x}$. Then $(\sigma \tau )x=\sigma (\tau x)=\sigma x=x$ and hence $\sigma \tau \in G_{x}$. Further $\sigma ^{-1}x=\sigma ^{-1}\sigma x=x$ and hence $\sigma ^{-1}\in G_{x}$.$\Box$

Theorem 1.8.12:

Let $Y\subseteq X$. If we write $\sigma Y:=\{\sigma y|y\in Y\}$ for each $\sigma \in G$, then

$G_{\sigma Y}=\sigma G_{Y}\sigma ^{-1}$.

Proof:

${\begin{aligned}\tau \in G_{\sigma Y}&\Leftrightarrow \tau \sigma Y=\sigma Y\\&\Leftrightarrow \sigma ^{-1}\tau \sigma Y=Y\\&\Leftrightarrow \sigma ^{-1}\tau \sigma Y\in G_{Y}\\&\Leftrightarrow \tau \in \sigma G_{Y}\sigma ^{-1}\end{aligned}}$$\Box$

Cardinality formulas

The following theorem will imply formulas for the cardinalities of $G_{x}$, $|G|$, $(G:G_{x})$ or $X$ respectively.

Theorem 1.8.13:

Let an action $G\times X\to X$ be given. The relation $x\sim y:\Leftrightarrow \exists \sigma \in G:\sigma x=y$ is an equivalence relation, whose equivalence classes are given by the orbits of the action. Furthermore, for each $x\in X$ the function

$\{\sigma G_{x}|\sigma \in G\}\to G(x),\sigma G_{x}\mapsto \sigma x$

is a well-defined, bijective function.

Proof:

1.

• Reflexiveness: $\iota x=\iota$
• Symmetry: $\sigma x=y\Leftrightarrow x=\sigma ^{-1}y$
• Transitivity: $\sigma x=y\wedge \tau y=z\Rightarrow (\tau \sigma )x=z$.

2.

Let $[x]$ be the equivalence class of $x$. Then

$y\in [x]\Leftrightarrow \exists \sigma \in G:\sigma x=y\Leftrightarrow y\in G(x)$.

3.

Let $\sigma G_{x}=\tau G_{x}$. Since $G_{x}\leq G$, $\tau ^{-1}\sigma \in G_{x}$. Hence, $\tau ^{-1}\sigma x=x\Leftrightarrow \tau x=\sigma x$. Hence well-definedness. Surjectivity follows from the definition. Let $\sigma x=\tau x$. Then $\tau ^{-1}\sigma x=x$ and thus $\tau ^{-1}\sigma G_{x}=G_{x}$. Hence injectivity.$\Box$

Corollary 1.8.14 (the orbit-stabilizer theorem):

Let an action $G\times X\to X$ be given, and let $x\in X$. Then

$|G(x)|=(G:G_{x})$, or equivalently $|G(x)|\cdot |G_{x}|=|G|$.

Proof: By the previous theorem, the function $\{\sigma G_{x}|\sigma \in G\}\to G(x),\sigma G_{x}\mapsto \sigma x$ is a bijection. Hence, $(G:g_{x})=|G(x)|$. Further, by Lagrange's theorem $(G:G_{x})={\frac {|G|}{|G_{x}|}}$.$\Box$

Corollary 1.8.15 (the orbit equation):

Let an action $G\times X\to X$ be given, and let $G(x_{1}),\ldots ,G(x_{n})$ be a complete and unambiguous list of the orbits. Then

$|X|=\sum _{j=1}^{n}\left|G\left(x_{j}\right)\right|=\sum _{j=1}^{n}(G:G_{x_{j}})$.

Proof: The first equation follows immediately from the equivalence classes of the relation from theorem 1.8.13 partitioning $X$, and the second follows from Corollary 1.8.14.$\Box$

Corollary 1.8.16:

Let an action $G\times X\to X$ be given, let $Z=\{x\in X|\forall \sigma \in G:\sigma x=x\}$, and let $G(x_{1}),\ldots ,G(x_{m})$ be a complete and unabiguous list of all nontrivial orbits (where the orbit of $x\in X$ is said to be trivial iff $G(x)=\{x\}$). Then

$|X|=|Z|+\sum _{j=1}^{m}\left|G\left(x_{j}\right)\right|$.

Proof: This follows from the previous Corollary and the fact that $|Z|$ equals the sum of the cardinalities the trivial orbits.$\Box$

The following lemma, which is commonly known as Burnside's lemma, is actually due to Cauchy:

Corollary 1.8.17 (Cauchy's lemma):

Let an action $G\times X\to X$ be given, where $G,X$ are finite. For each $\sigma \in G$, we denote ${\displaystyle }$.

The class equation

Definition 1.8.18:

Let a group $G$ act on itself by conjugation, i. e. $\sigma x:=\sigma x\sigma ^{-1}$ for all $\sigma ,x\in G$. For each $x\in G$, the centraliser of $x$ is defined to be the set

${\mathcal {C}}_{G}(x):=G_{x}$.

Using the machinery we developed above, we may now set up a formula for the cardinality of $G$. In order to do so, we need a preliminary lemma though.

Lemma 1.8.19:

Let $G$ act on itself by conjugation, and let $x\in G$. Then the orbit of $x$ is trivial if and only if $x\in Z(G)$.

Proof: $x\in Z(G)\Leftrightarrow \forall \sigma \in G:\sigma x\sigma ^{-1}=x\Leftrightarrow G(x)=\{x\}$.$\Box$

Corollary 1.8.20 (the class equation):

Let $G$ be a group acting on itself by conjugation, and let $G(x_{1}),\ldots ,G(x_{m})$ be a complete and unambiguous list of the non-trivial orbits of that action. Then

$|G|=|Z(G)|+\sum _{j=1}^{m}(G:{\mathcal {C}}_{G}(x_{j}))$.

Proof: This follows from lemma 1.8.19 and Corollary 1.8.16.$\Box$

Special topics

Equivariant functions

A set together with a group acting on it is an algebraic structure. Hence, we may define some sort of morphisms for those structures.

Definition 1.8.21:

Let a group $G$ act on the sets $X$ and $Y$. A function $f:X\to Y$ is called equivariant iff

$\forall \sigma \in G,x\in X:\sigma f(x)=f(\sigma x)$.

Lemma 1.8.22:

p-groups

We shall now study the following thing:

Definition 1.8.24:

Let $p$ be a prime number. If $G$ is a group such that $|G|=p^{k}$ for some $k\in \mathbb {N}$, then $G$ is called a $p$-group.

Corollary 23: Let $G$ be a $p$-group acting on a set $S$. Then $|S|\equiv |Z|\ \mathrm {mod} \ p$.

Proof: Since $G$ is a $p$-group, $p$ divides $|G*a|$ for each $a\in A$ with $A$ defined as in Lemma 21. Thus $\sum _{a\in A}|G*a|\equiv 0\ \mathrm {mod} \ p$. ∎

Group Representations

Linear group actions on vector spaces are especially interesting. These have a special name and comprise a subfield of group theory on their own, called group representation theory.　We will only touch slightly upon it here.

Definition 24: Let $G$ be a group and $V$ be a vector space over a field $F$. Then a representation of $G$ on $V$ is a map $\Phi \,:\,G\times V\rightarrow V$ such that

i) $\Phi (g)\,:\,V\rightarrow V$ given by $\Psi (g)(v)=\Psi (g,v)$, $v\in V$, is linear in $v$ over $F$.

ii) $\Phi (e,v)=v$

iii) $\Phi \left(g_{1},\Phi (g_{2},v)\right)=\Phi (g_{1}g_{2},v)$ for all $g_{1},g_{2}\in G$, $v\in V$.

V is called the representation space and the dimension of $V$, if it is finite, is called the dimension or degree of the representation.

Remark 25: Equivalently, a representation of $G$ on $V$ is a homomorphism $\phi \,:\,G\rightarrow GL(V,F)$. A representation can be given by listing $V$ and $\phi$, $(V,\phi )$.

As a representation is a special kind of group action, all the concepts we have introduced for actions apply for representations.

Definition 26: A representation of a group $G$ on a vector space $V$ is called faithful or effective if $\phi \,:\,G\rightarrow GL(V,F)$ is injective.

Composition series

Definitions 2.7.1:

Let $G$ be a group. A normal series of $G$ are finitely many subgroups $N_{1},\ldots ,N_{n}$ of $G$ such that

$\{e\}=N_{n}\triangleleft N_{n-1}\triangleleft \cdots \triangleleft N_{1}=G$

Two normal series $N_{1},\ldots ,N_{n}$ and $M_{1},\ldots ,M_{k}$ of $G$ are equivalent if and only if $n=k$ and there exists a bijective function $\sigma :\{1,\ldots ,n\}\to \{1,\ldots ,n\}$ such that for all $j\in \{1,\ldots ,n-1\}$:

$N_{j}/N_{j+1}\cong M_{\sigma (j)}/M_{\sigma (j)+1}$

A normal series $N_{1},\ldots ,N_{n}$ of $G$ is a composition series of $G$ if and only if for each $j\in \{1,\ldots ,n-1\}$ the group

$N_{j}/N_{j+1}$

is simple.

Theorem 2.7.2:

Let $G$ be a finite group. Then there exists a composition series of $G$.

Proof:

We prove the theorem by induction over $|G|$.

1. $|G|=1$. In this case, $G$ is the trivial group, and $M_{1}$ with $M_{1}=G$ is a composition series of $G$.

2. Assume the theorem is true for all $n\in \mathbb {N}$, $n<|G|$.

Since the trivial subgroup $\{e\}\subset G$ is a normal subgroup of $G$, the set of proper normal subgroups of $G$ is not empty. Therefore, we may choose a proper normal subgroup $N$ of maximum cardinality. This must also be a maximal proper normal subgroup, since any group in which it is contained must have at least equal cardinality, and thus, if $M$ is normal such that

$N\subsetneq M\subsetneq G$

, then

$|M|>|N|$

, which is why $N$ is not a proper normal subgroup of maximal cardinality.

Due to theorem 2.6.?, $G/N$ is simple. Further, since $|N|<|G|$, the induction hypothesis implies that there exists a composition series of $N$, which we shall denote by $N_{2},\ldots ,N_{n}$, where

$\{e\}=N_{n}\triangleleft N_{n-1}\triangleleft \cdots \triangleleft N_{2}=N$

. But then we have

$\{e\}=N_{n}\triangleleft \cdots \triangleleft N_{2}=N\triangleleft N_{1}:=G$

, and further for each $m\in \{1,\ldots ,n-1\}$:

$N_{m}/N_{m+1}$ is simple.

Thus, $N_{1},\ldots ,N_{n}$ is a composition sequence of $G$.$\Box$

Our next goal is to prove that given two normal sequences of a group, we can find two 'refinements' of these normal sequences which are equivalent. Let us first define what we mean by a refinement of a normal sequence.

Definition 2.7.3:

Let $G$ be a group and let $N_{1},\ldots ,N_{n}$ be a normal sequence of $G$. A refinement of $N_{1},\ldots ,N_{n}$ is a normal sequence $N_{1}',\ldots ,N_{k}'$ such that

$\{N_{1},\ldots ,N_{n}\}\subseteq \{N_{1}',\ldots ,N_{k}'\}$

Theorem 2.7.4 (Schreier):

Let $G$ be a group and let $N_{1},\ldots ,N_{n}$, $M_{1},\ldots ,M_{k}$ be two normal series of $G$. Then there exist refinements $N_{1}',\ldots ,N_{m}'$ of $N_{1},\ldots ,N_{n}$ and $M_{1}',\ldots ,M_{l}'$ of $M_{1},\ldots ,M_{k}$ such that $N_{1}',\ldots ,N_{m}'$ and $M_{1}',\ldots ,M_{l}'$ are equivalent.

Proof:

Theorem 2.7.5 (Jordan-Hölder):

Let $G$ be a group and let $N_{1},\ldots ,N_{n}$ and $M_{1},\ldots ,M_{k}$ be two composition series of $G$. Then $N_{1},\ldots ,N_{n}$ and $M_{1},\ldots ,M_{k}$ are equivalent.

Proof:

Due to theorem 2.6.?, all the elements of $\{N_{1},\ldots ,N_{n}\}$ must be pairwise different, and the same holds for the elements of $\{M_{1},\ldots ,M_{k}\}$.

Due to theorem 2.7.4, there exist refinements $N_{1}',\ldots ,N_{m}'$ of $N_{1},\ldots ,N_{n}$ and $M_{1}',\ldots ,M_{l}'$ of $M_{1},\ldots ,M_{k}$ such that $N_{1}',\ldots ,N_{m}'$ and $M_{1}',\ldots ,M_{l}'$ are equivalent.

But these refinements satisfy

$\{N_{1}',\ldots ,N_{m}'\}=\{N_{1},\ldots ,N_{n}\}$

and

$\{M_{1}',\ldots ,M_{l}'\}=\{M_{1},\ldots ,M_{k}\}$

, since if this were not the case, we would obtain a contradiction to theorem 2.6.?.

We now choose a bijection $\sigma :\{1,\ldots ,m\}\to \{1,\ldots ,m\}$ such that for all $j\in \{1,\ldots ,m-1\}$:

$N_{j}/N_{j+1}\cong M_{\sigma (j)}/M_{\sigma (j)+1}$

Group Theory/The Sylow Theorems

In this section, we will have a look at the Sylow theorems and their applications. The Sylow theorems are three powerful theorems in group theory which allow us for example to show that groups of a certain order $d\in \mathbb {N}$ are not simple.

The proofs are a bit difficult but nonetheless interesting. Important remark: Wikipedia also has proofs of the Sylow theorems, see Wikipedia article on the Sylow theorems, which are shorter and more elegant. But here you can find other proofs. This is because the author wanted to avoid redundancy. So you can choose the proof you like, or read both :-)

Remark: The proofs below also teach a lot about how to apply group actions, so they might give you also an idea how to do this kind of stuff :-)

The Sylow theorems

Definition 1: Let $G$ be a finite group of order $mp^{a}$, where $p$ is a prime, $a,m\in \mathbb {N}$ and $m$ is coprime to $p^{a}$. We say that a subgroup of $G$ is a Sylow $p$-subgroup iff it has order $p^{a}$.

Definition 2: Let H be a subgroup of a group G. We define the normalizer N[H] of H as follows:

$N[H]:=\{g\in G:gHg^{-1}=H\}$ due to Fermat

Theorem 3 (Cauchy's theorem) Let G be a group and $p$ be a prime number such that $p$ divides $|G|$. Then there exists an element of G which has order p. In particular, there is a subgroup of order p of G, namely $<p>$.

Proof: Let X be the set of all tuples $(x_{1},\ldots ,x_{p}),\forall 1\leq i\leq p:x_{i}\in G$ for which $x_{1}\cdots x_{p}=1$. The cyclic group $\mathbb {Z} /p\mathbb {Z}$ acts on X with the action $d*(x_{1},\ldots ,x_{p})=(x_{d+1},\ldots ,x_{p},x_{1},\ldots ,x_{d})$. An example is $(1,\ldots ,1)$, for which the orbit contains only this same element ($(1,\ldots ,1)$).

We also have that $|X|=|G|^{p-1}$ since we can choose the first p-1 elements arbitrarily and $x_{p}=(x_{1}\cdots x_{p-1})^{-1}$, and therefore |X| is a multiple of p, because |G| is also divisible by p. Furthermore, we know by the orbit-stabilizer theorem (theorem 19 from the section about group actions), that $\forall x\in X:|\mathbb {Z} /p\mathbb {Z} *x||\mathbb {Z} /p\mathbb {Z} _{x}|=|\mathbb {Z} /p\mathbb {Z} |=p$. Since p is a prime number, we have for all $x\in X:$ that either $|\mathbb {Z} /p\mathbb {Z} *x|=1$ or $|\mathbb {Z} /p\mathbb {Z} *x|=p$. But since the orbits partition X (due to lemma 11 from the section about group actions), and $|X|$ is divisible by p, we need at least one (in the case p = 2, else even more elements) other element $x'\neq (1,\dots ,1)$ of X such that $|\mathbb {Z} /p\mathbb {Z} *x'|=1$. Let $x'=(x_{1}',\ldots ,x_{p}')$. We have $x_{1}'=\cdots =x_{p}'$, because otherwise x' would not be fixed by the action we defined. Then $x_{1}'^{p}=x_{1}'\cdots x_{p}'=1$. QED.

Theorem 4 (Sylow I): Let $G$ be a finite group of order $mp^{a}$, where $p$ is a prime, $a,m\in \mathbb {N}$ and $m$ is coprime to $p$. For every $0\leq i\leq a$, there is a subgroup of order $p^{i}$ of G. In particular, there exists a Sylow $p$-subgroup of G.

Proof: For this proof, we use induction. Let H be a p-subgroup of G, i. e. $|H|=p^{i}$ for some natural i. H acts on the sets of left cosets G/H by left multiplication. By corollary 23 from the section about group actions, we obtain that $|G/H|\equiv |Z|\mod p(*)$, where $Z=\{gH\in G/H:\forall h\in H:hgH=gH\}$. But also the following equivalences are true:

$\forall h\in H:hgH=gH\Leftrightarrow \forall h\in H:hg\in gH\Leftrightarrow \forall h\in H:g^{-1}hg\in H$ $\Leftrightarrow gHg^{-1}\subseteq H\Leftrightarrow gHg^{-1}=H$ because $|H|=|gHg^{-1}|$ $\Leftrightarrow g\in N[H]$

But from this we can conclude that $Z=\{gH\in G/H:g\in N[H]\}=N[H]/H$. Therefore, (*) becomes $[G:H]\equiv [N[H]:H]\mod p$. From this we can conclude, that if $i<a$, and therefore p divides $[G:H]$ by the theorem of Lagrange, that then also p divides $[N[H]:H]$. And also: Since $H$ is a normal subgroup of $N[H]$, we know that $N[H]/H$ is a group. Therefore we can apply Cauchy's theorem: $N[H]/H$ has a subgroup $N$ of order p. But if we set $H'=\bigcup _{gH\in N}gH$, then $H'$ is a subgroup of $G$ of order $p^{i+1}$, because
a) the intersection of two different cosets is the empty set, and
b) $H'$ is a subgroup of G because for $gh,g'h'\in H'$ $gh(g'h')^{-1}=ghh'^{-1}g'^{-1}=gg'^{-1}h''h'''\in H'$ for some $h'',h'''\in H$, because $g\in N[H]$, the normaliser. QED.

Lemma 5 (order of the conjugate): Let G be a group with identity $Id_{G}$, and $g\in G$ an element of that group. Then $\forall x\in G:ord(g)=ord(xgx^{-1})$

Proof: First, we observe that $(xgx^{-1})^{n}=xg^{n}x^{-1}$ by induction: For n = 1, the claim is obviously true, and the calculation

$(xgx^{-1})^{n+1}=xg^{n}x^{-1}xgx^{-1}=xg^{n+1}x^{-1}$

shows the induction step.

Therefore, $(xgx^{-1})^{ord(g)}=xg^{ord(g)}x^{-1}=Id_{G}$, which shows that $ord(xgx^{-1})\leq ord(g)$.

Let furthermore $k\in \mathbb {N}$. Then $(xgx^{-1})^{n}=xg^{k}x^{-1}=Id_{G}\Rightarrow g^{k}x^{-1}=x^{-1}\Rightarrow g^{k}=Id_{g}$, where the first implication is true because the inverse is uniquely determined, and the second implication is true because the identity is uniquely determined. Therefore $ord(xgx^{-1})\geq ord(g)$, implying with the former inequality that $ord(g)=ord(xgx^{-1})$ and finishing the proof. QED.

Lemma 6: Let $X=\{gPg^{-1}:g\in G\}$, and let G act on X by conjugation. Then $G_{p}$ is a subgroup of G, and any p-subgroup of $G_{P}$ is contained in P.

Proof: Conjugation of G on X is a transitive action: If $g,g'\in G$ are arbitrary, $h*gPg^{-1}=g'Pg'^{-1}$ by choosing $h=g'g^{-1}$. By the section about group actions, transitivity implies $G_{P}$ is really a group.

By the definition of X, we have that P is even a normal subgroup of $G_{P}$. Let now Q be an arbitrary p-subgroup of $G_{P}$. Then $QP$ is a subgroup due to the section about normal subgroups. Due to the second isomorphism theorem, we have that $QP/P\approx Q/(Q\cap P)$. Therefore, we also have by Lagrange's theorem, that $|QP/P|=|Q/(Q\cap P)|={\frac {|Q|}{|Q\cap P|}}=p^{s}$ for some $s\in \mathbb {N} _{0}$, because Q is a Sylow p-subgroup. Furthermore, Lagrange's theorem also assures that $|QP/P|={\frac {|QP|}{|P|}}$. Since P is a Sylow p-subgroup and QP is a subgroup of G and therefore $|QP|$ divides |G|, we know that p does not divide $|QP/P|$. Therefore, $|QP/P|$ must be the trivial subgroup, and therefore also $Q/(Q\cap P)$, which implies $Q\cap P=Q$ because $gH=H\Leftrightarrow g\in H$ due to the section about subgroups, QED.

Theorem 7 (Sylow II): If P is a Sylow p-subgroup of G, and Q is an arbitrary p-group of G, then $\exists g\in G:Q\subseteq gPg^{-1}$, so Q is contained in a Sylow p-group, since for arbitrary groups G if $H$ is an arbitrary subgroup of G, then also $gHg^{-1}$. In particular, all Sylow $p$-subgroup of $G$ are conjugate.

Proof: Let's choose $X=\{gPg^{-1}:g\in G\}$. P acts on X by conjugation. By the orbit-stabilizer theorem (corollary 19 of the section on group actions), we have that $\forall x\in X:|P*x|={\frac {|P|}{|P_{x}|}}$. But since P is a Sylow p-group, we know that $|P*x|\equiv 0\mod p$ or $|P*x|\equiv 1\mod p$. Since $\forall h\in P:hPh^{-1}=P$, we furthermore have $P*P=\{P\}$ and therefore $|P*P|=1$, because P is a single element in X.

But P is also the only element with trivial orbit: Let $gPg^{-1}\in X$. That $gPg^{-1}$ has trivial orbit means translated into the language of our group action, that $\forall x\in P:xgPg^{-1}x^{-1}=gPg^{-1}$. If we multiply this equation by $g$ on the right and $g^{-1}$ on the left, we obtain that $\forall x\in P:g^{-1}xg\in P_{P}$. Because of Lemma 5 we know that $|gxg^{-1}|=|x|$. Therefore $gPg^{-1}$ is a p-subgroup of $P_{P}$. Due to Lemma 6, we know that therefore $gPg^{-1}$ must be a subgroup of P, and since both sets contain the same number of elements, they must be equal.

We now recall the above formula $\forall x\in X:|P*x|={\frac {|P|}{|P_{x}|}}$ and note that since $|P*x|=p^{s},s\in \mathbb {N} _{0}$, all the other elements must have the property $|P*x|\equiv 0\mod p$, since their orbits are not trivial. Since the orbits partition X, we have that $|X|\equiv 1\mod p$.

Now we let Q act on X by conjugation, instead of P. Since $|X|\equiv 1\mod p$, we know that there is at least one orbit of length 1. So what does this mean?:

$\exists g\in G:\forall x\in Q:x(gPg^{-1})x^{-1}=gPg^{-1}$

As before:

$g^{-1}Qg\subseteq Q_{P}$

, and, by Lemma 6:

$g^{-1}Qg\subseteq P$, and therefore $Q\subseteq gPg^{-1}$. QED.

Lemma 8: The normalizer of a subgroup is a subgroup.

Proof: Let H be a subgroup of G, and let G act on H by conjugation. Then the normalizer of H is the stabilizer of H in this action. Therefore, it is a subgroup due to Lemma 14 of the section about group actions, QED.

Theorem 9 (Sylow III*): Let again $n_{p}$ be the number of Sylow $p$-groups of $G$. Then $n_{p}=|G/N[P]|$, where $P$ is any Sylow $p$-group.

Proof: This follows from the proof of Sylow II and the thm. Sylow II itself: Choose $X$ as in the proof of Sylow II. Then by the theorem itself follows that $|X|=n_{p}$, and if we consider the group action of G on X of conjugation, then we have that $\forall x\in X:|G*P|=n_{p}$. But since due to the orbit-stabilizer theorem (thm. 19 in the section about group actions) $|G*P|={\frac {|G|}{|G_{P}|}}={\frac {|G|}{|N[P]|}}$ due to the definition of the normalizer, and ${\frac {|G|}{|N[P]|}}=|G/N[P]|$ due to the theorem of Lagrange (which is applicable since N[P] is a subgroup due to Lemma 8), the theorem follows. QED.

Theorem 10 (Sylow III): Let $G$ be a finite group of order $mp^{a}$, where $p$ is a prime, $a,m\in \mathbb {N}$ and $m$ is coprime to $p$. If $n_{p}$ is the number of Sylow $p$-subgroups of $G$, then $n_{p}\mid m$ and $n_{p}\equiv 1\mod p$.

Proof: Choose $X$ as in the proof of Sylow II. The proof for Sylow II shows that $|X|\equiv 1\mod p$, and the theorem Sylow II itself shows that $|X|=n_{p}$. This proves the second part. The first part follows from Sylow III* and the fact that $|G/N[P]|={\frac {|G|}{|N[P]|}}$ due to Lagrange (which we can apply here because N[P] is a subgroup due to Lemma 8): Since P is a subgroup of N[P], we know that $|P|$ divides $|N[P]|$. This means that $|G/N[P]|$ is not divisible by p. But since $|G/N[P]|$ divides $|G|=mp^{a}$, it must divide m. QED.

How to show that groups of a certain order aren't simple

In this section, it will be shown how to show that groups of a certain order can not be simple using the Sylow theorems. This is a useful application of the Sylow theorems.

Example 11: Groups of order 340 are not simple.

Proof: Let |G| = 340 = 2² ⋅ 5 ⋅ 17. Due to Sylow III, we have that $n_{5}=1$, because $n_{5}\equiv 1\mod 5$ and $n_{5}|2^{2}\cdot 17$ has only this solution (this can be seen by computing all possible solutions, which are finitely many since the last condition implies that $n_{5}\leq 2^{2}\cdot 17$). But since, due to Sylow II, the conjugate of the only Sylow 5-group is again a Sylow 5-group, it is itself. This is the definition of normal subgroups. Therefore, by the definition of simple groups, groups of order 340 are not simple. QED.

Example 12: Groups of order 48 are not simple.

Proof: Let |G| = 48 = 2⁴ ⋅ 3. Sylow III tells us that $n_{2}\equiv 1\mod 2$ and $n_{2}|3$. From this follows that either $n_{2}=1$ or $n_{2}=3$. If now $n_{2}=1$, then, in the same way as example 11, the (then only) Sylow 2-group is normal. In the other case, through conjugation on the set of the three Sylow 2-groups, we generate a homomorphism $\phi :G\to S_{3}$. This is due to theorem 2 from the section about group actions. The image can't be trivial, because all Sylow 2-groups are conjugate because of Sylow II. But since the kernel is a normal subgroup, and $|S_{3}|=6$, we have that due to the first isomorphism theorem and the theorem of Lagrange, that the kernel is a proper, non-trivial normal subgroup, which is why the group is not simple.

Example 13: Groups of order 108 are not simple.

Proof: Let |G| = 108 = 2 ⋅ 2 ⋅ 3³ and S be a Sylow 3-group. We let G act on the cosets of S by left multiplication. Due to theorem 2 from the section about group actions, we know that this action generates a homomorphism $\varphi :G\to S_{4}$. Due to the first isomorphism theorem and Lagrange, we have that $|G|=|ker\varphi ||\varphi (G)|$ and therefore $|\varphi (G)|$ must divide 108. Since $\varphi (G)$ is a subgroup in $S_{4}$ and $|S_{4}|=24$, $|\varphi (G)|$ must divide 24. From this follows that $|\varphi (G)|\leq 12$, and therefore, again due to the formula $|G|=|ker\varphi ||\varphi (G)|$ from the first isomorphism theorem and Lagrange, we have that $|ker\varphi |\geq {\frac {108}{12}}=9$. If the kernel would be G, then the action would be trivial and therefore $S=G$, which is a contradiction, since G is no Sylow 3-group. Therefore, the kernel is a proper, non-trivial normal subgroup, which is why the group is not simple.

Rings

This section builds upon and expands the theory covered in the previous chapter on groups. The reader is strongly advised to master the material presented in the sections up to and including Products and Free Groups before continuing.

Motivation

The standard motivation for the study of rings is as a generalization of the set of integers $\mathbb {Z}$ with addition and multiplication, in order to study integer-like structures in a more general and less restrictive setting. However, we will also present the following motivation for the study of rings, based on the theory of Abelian groups.

Let $G$ and $H$ be Abelian groups. Then the set $\mathrm {Hom} _{\mathrm {Ab} }(G,H)$ (Please don't pay much attention to the subscript for now.) of group homomorphisms $\phi \,:\,G\rightarrow H$ naturally forms an abelian group in the following way. If $\phi ,\psi \in \mathrm {Hom} _{\mathrm {Ab} }(G,H)$, define $(\phi +\psi )(g)=\phi (g)+\psi (g)$ for all $g\in G$. It should be obvious where each addition is taking place. In particular, we can consider the set $\mathrm {End} _{\mathrm {Ab} }(G)=\mathrm {Hom} _{\mathrm {Ab} }(G,G)$ of endomorphisms of $G$. That is, the set of homomorphisms from $G$ to itself. This set is obviously a group from the above discussion, but it is also closed under composition. By endowing the set $\mathrm {End} _{\mathrm {Ab} }(G)$ with the operations of addition, $+$, and composition, $\circ$, we note that it has the following properties:

i) It is an Abelian group under addition.

ii) It is a monoid under multiplication.

iii) Addition distributes over composition.

Indeed, for the third property, note that if $\phi ,\psi ,\xi \in \mathrm {End} _{\mathrm {Ab} }(G)$ and $g\in G$, then $\phi \circ (\psi +\xi )(g)=(\phi \circ \psi +\phi \circ \xi )(g)$ and $(\phi +\psi )\circ \xi (g)=(\phi \circ \xi +\psi \circ \xi )(g)$. The following material is a generalization of this situation.

Introduction to Rings

Definition 1: A ring $(R,+,\cdot )$ is a set $R$ with two binary operations $+$ and $\cdot$ that satisfies the following properties:

For all $a,b,c\in R,$

i) $(R,+)$ is an abelian group.

ii) $(R,\cdot )$ is a monoid.

The definition of ring homomorphism does not include the existence of 1.

iii) $\cdot$ is distributive over $+$:

1) $a\cdot (b+c)=(a\cdot b)+(a\cdot c)$

2) $(a+b)\cdot c=(a\cdot c)+(b\cdot c)$

We will denote the additive identity in a ring by $0_{R}$ or $0$ if the ring is understood. Similarily, we denote the multiplicative identity by $1_{R}$ or $1$ when the ring is understood. We'll often use juxtaposition in place of $\cdot$, i.e., $ab\,$ for $a\cdot b$.

Remark 2: Some authors do not require their rings to have a multiplicative identity element. We will call a ring without an idenitity a rng. Pseudo-rings is another term used for rings without unity. Authors who do not require a multiplicative identity usually call a ring a ring with unity. Unless otherwise stated, we will assume that $0\neq 1$ in our rings. A major part of noncommutaive ring theory was developed without assuming every ring has an identity element.

Example 3: The reader is already familiar with several examples of rings. For instance $\mathbb {Z} ,\mathbb {Q} ,\mathbb {R}$ and $\mathbb {C}$ with the usual addition and multiplication operations. We have a familiy of finite rings given by the sets $\mathbb {Z} _{n}$ for integer $n\geq 2$ with addition and multiplication defined modulo $n$. Finally we have an example of a rng given by the sets $n\mathbb {Z}$ for integer $n\geq 2$ with the usual addition and multiplication. The reader is invited to confirm the ring axioms for these examples.

Let us now prove some very basic properties about rings. This is analogous to what we did for groups when we first introduced them.

Theorem 4: Let $R$ be a ring, and let $a,b,c\in R$. Then the following are true:

1. If $a+b=a+c$, then $b=c$.
2. The equation $a+x=b$ has a unique solution.
3. $-(-a)=a$
4. $0a=0$
5. $(-a)b=-(ab)$
6. $(-a)(-b)=ab$

Proof: (1), (2), and (3) all strictly concern addition, and are all previous results from $(R,+)$ being a group. The other three parts all concern both addition and multiplication (since 0 and - are additive concepts), so as a proof strategy we expect to use the distributive law in some way to link the two operations. For (4), observe that $0a+0a=(0+0)a=0a=0a+0$. But then by (1), 0a=0. For (5), Note that $(-a)b+ab=(-a+a)b=0b=0$. For (6) note that $(-a)(-b)+-(ab)=(-a)(-b)+(-a)b=-a(-b+b)=-a0=0$. ∎

Remark 5: Take another look at the examples in Example 3. Notice that for all those rings, multiplication is a commutative opration. However, the axioms say nothing about this. Thus we should expect to find counter-examples to this.

Definition 6: A ring is called commutative if multiplication is commutative.

Example 7: An example of a non-commutative ring is the set ${M}_{n}(\mathbb {R} )$ of $n\times n$ square matrices with real coefficients under standard addition and multiplication of matrices, where $n\geq 2$ is an integer. The reader can easily check this for $n=2$ and conclude that it holds for all other $n$ (why?).

Theorem 8: A ring has a unique multiplicative identity.

Proof: During our brief discussion of monoids earlier, we showed that in any monoid the identity is unique. Since a ring sans addition is a monoid, this applies here. ∎

Example 9: The singleton set $\{*\}$ with addition and multiplication defined by $*+*=*$ and $*\cdot *=*$ is a ring, called the trivial ring or the zero ring. Note that in the trivial ring, $0=1$. The reader is invited to show that $0=1$ in a ring if and only if it is the trivial ring.

If the reader has tried to construct some of the rings $=\mathbb {Z} _{n}$, he/she may have realised that certain non-zero elements have product zero. We formalize this concept as follows.

Definition 10: Let $R$ be a ring and $a\in R\setminus \{0\}$. $a$ is called a left(resp.right)-zero-divisor if there exists a $b\in R$ such that $ab=0$ $(ba=0)$.

Lemma 11: Let $R$ be a ring with $a\in R$. Define the function $\rho _{a}\,:\,R\rightarrow R$ given by $\rho _{a}(r)=ar$ for all $r\in R$. Then $\rho _{a}$ is injective if and only if $a$ is not a left-zero-divisor.

Proof: Assume $a$ is not a left-zero-divisor, and assume we have $ab=\rho _{a}(b)=\rho _{a}(c)=ac$ for some $b,c\in R$. This implies $ab-ac=a(b-c)=0$, giving $b=c$ since $a$ is not a left-zero-divisor, so $\rho _{a}$ is injective. Conversely, assume $a$ is a left-zero-divisor. Then there exists a $b\in R$ such that $b\neq 0$ and $\rho _{a}(b)=ab=0=a0=\rho _{a}(0)$, so $\rho _{a}$ is not injective. ∎

Remark 12: Thus, multiplication by $a$ is left-cancellative if and only if $a$ is not a zero-divisor. The reader is invited to state and prove the equivalent lemma for right-zero-divisors.

Example 13: $\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C}$ are all examples of commutative rings without zero divisors. These rings motivate the next definition.

Definition 14: Let $R$ be a commutative ring without zero divisors. Then $R$ is called an integral domain.

Just like Definition 14, the majority of special types of rings will be motivated by properties of $\mathbb {Z}$.

Example 15:

1. The set $\mathrm {Hom} _{\mathrm {Set} }(\mathbb {R} ,\mathbb {R} )$ of functions on $\mathbb {R}$ with pointwise addition and multiplication is a ring.
2. More generally, if $R$ is a ring, the set $\mathrm {Hom} _{\mathrm {Set} }(R,R)$ of functions from $R$ to itself is also a ring.
3. The set $\mathrm {Hom} _{\mathrm {Set} }(R,R)$ with function composition for multiplication is not a ring since the statement $f\circ (g+h)=f\circ g+f\circ h$ is not true in general.
4. The set of integrable functions on the real numbers, $L^{1}$, is a rng under pointwise addition and multiplication given by convolution: $(f*g)(t)=\int _{\mathbb {R} }f(\tau )g(t-\tau )d\tau$. This rng is important to the study of linear systems and differential equations. If the reader has enough calculus under his/her belt, he/she reader is invited to show that it does not have an identity, and that it is commutative.
5. The set of Gaussian integers $\mathbb {Z} \left[i\right]=\left\{a+bi|a,b\in \mathbb {Z} \right\}$ with standard addition and multiplication is a ring.

Definition 16: Let $R$ be a ring. An element $a\in R$ is a unit and is invertible if there is an element $b\in R$ such that $ab=ba=1$. The set of all units is denoted by $R^{*}$.

Exercise 17: Prove that $R^{*}$ is a group under multiplication.

Exercise 18:: Show that a zero-divisor is not a unit.

Theorem 19: (Cancellation Law for Integral Domains): Let $R$ be an integral domain, and let $a,b,c\in R$ be nonzero. Then $ab=ac$ if and only if $b=c$.

Proof: Evidently $ab=ac$ if $b=c$. To see the other direction, we rearrange the equality as $ab-ac=0$. But then $a(b-c)=0$. Since $a$ is nonzero, and $R$ contains no zero divisors, it must be the case that $b-c=0$, which is to say that $b=c$.

Definition 20: A ring $R$ is a division ring or skew field if all non-zero elements are units, i.e. if it forms a group under multiplication with its nonzero elements.

Definition 21: A field is a commutative division ring. Alternatively, a field $F$ is a ring where $(F-{0},\cdot )$ is an abelian group under multiplication. As another alternative, a field is an integral domain where all non-zero elements are invertible.

As stated before, integral domains are easy to work with because they are so close to being fields. In fact, the next theorem shows just how close the two are:

Theorem 22: Let $R$ be a finite integral domain. Then $R$ is a field.

Proof: Let $a\in R$ be nonzero and let $S=\left\{ab|b\in R\right\}$. Clearly $S$ is a subset of $R$. From the cancellation law, we can see that $|S|=|R|$ (since if two elements $ab$ and $ac$ are equal, then $b=c$). But then $S=R$. So then there must be some $b$ such that $ab=1$. So $a$ is a unit.

Of course proving that a set with two operations satisfy all of the ring axioms can be tedious. So, just as we did for groups, we note that if we're considering a subset of something that's already a ring, then our job is easier.

Definition 23: A subring $S$ of a ring $R$ is a subset of $R$ that is also a ring (under the same two operations as for $R$) and $1_{S}=1_{R}$. We denote "$S$ is a subring of $R$" by $S\leq R$. Note many mathematicians do not require rings or subrings to have an identity.

Theorem 24: Let $S\neq \emptyset$ be a subset of a ring $R$. Then $S\leq R$ if and only if for all $a,b\in S$,

1. $a-b\in S$,
2. $ab\in S$,
3. $1\in S$.

Example 25:

1. $\mathbb {Z} \leq \mathbb {Q} \leq \mathbb {R} \leq \mathbb {C}$.
2. The trivial ring $\left\{0\right\}$ is a subring of every ring.
3. The set of Gaussian integers $\mathbb {Z} \left[i\right]$ is a subring of the complex numbers $\mathbb {C}$.

Ring Homomorphisms

Just as with groups, we can study homomorphisms to understand the similarities between different rings.

Homomorphisms

Definition

Let R and S be two rings. Then a function $f:R\to S$ is called a ring homomorphism or simply homomorphism if for every $r_{1},r_{2}\in R$, the following properties hold:

$f(r_{1}r_{2})=f(r_{1})f(r_{2}),$

$f(r_{1}+r_{2})=f(r_{1})+f(r_{2}).$

In other words, f is a ring homomorphism if it preserves additive and multiplicative structure.

Furthermore, if R and S are rings with unity and $f(1_{R})=1_{S}$, then f is called a unital ring homomorphism.

Examples

1. Let $f:\mathbb {Z} \to M_{2}(\mathbb {Z} )$ be the function mapping $a\mapsto {\begin{pmatrix}a&0\\0&0\end{pmatrix}}$. Then one can easily check that $f$ is a homomorphism, but not a unital ring homomorphism.
2. If we define $g:a\mapsto {\begin{pmatrix}a&0\\0&a\end{pmatrix}}$, then we can see that $g$ is a unital homomorphism.
3. The zero homomorphism is the homomorphism which maps ever element to the zero element of its codomain.

Theorem: Let $R$ and $S$ be integral domains, and let $f:R\to S$ be a nonzero homomorphism. Then $f$ is unital.

Proof: $1_{S}f(1_{R})=f(1_{R})=f(1_{R}^{2})=f(1_{R})f(1_{R})$. But then by cancellation, $f(1_{R})=1_{S}$.

In fact, we could have weakened our requirement for R a small amount (How?).

Theorem: Let $R,S$ be rings and $\varphi :R\to S$ a homomorphism. Let $R'$ be a subring of $R$ and $S'$ a subring of $S$. Then $\varphi (R')$ is a subring of $S$ and $\varphi ^{-1}(S')$ is a subring of $R$. That is, the kernel and image of a homomorphism are subrings.

Proof: Proof omitted.

Theorem: Let $R,S$ be rings and $\varphi :R\to S$ be a homomorphism. Then $\varphi$ is injective if and only if $\ker \varphi =0$.

Proof: Consider $\varphi$ as a group homomorphism of the additive group of $R$.

Theorem: Let $F,E$ be fields, and $\varphi :F\to E$ be a nonzero homomorphism. Then $\varphi$ is injective, and $\varphi (x)^{-1}=\varphi (x^{-1})$.

Proof: We know $\varphi (1)=1$ since fields are integral domains. Let $x\in F$ be nonzero. Then $\varphi (x^{-1})\varphi (x)=\varphi (x^{-1}x)=\varphi (1)=1$. So $\varphi (x)^{-1}=\varphi (x^{-1})$. So $\varphi (x)\neq 0$ (recall you were asked to prove units are nonzero as an exercise). So $\ker \varphi =0$.

Isomorphisms

Definition

Let $R,S$ be rings. An isomorphism between $R$ and $S$ is an invertible homomorphism. If an isomorphism exists, $R$ and $S$ are said to be isomorphic, denoted $R\cong S$. Just as with groups, an isomorphism tells us that two objects are algebraically the same.

Examples

1. The function $g$ defined above is an isomorphism between $\mathbb {Z}$ and the set of integer scalar matrices of size 2, $S=\left\{\lambda I_{2}|\lambda \in \mathbb {Z} \right\}$.
2. Similarly, the function $\varphi :\mathbb {C} \to M_{2}(\mathbb {R} )$ mapping $z\mapsto {\begin{pmatrix}a&-b\\b&a\end{pmatrix}}$ where $z=a+bi$ is an isomorphism. This is called the matrix representation of a complex number.
3. The Fourier transform ${\mathcal {F}}:L^{1}\to L^{1}$ defined by ${\mathcal {F}}(f)=\int _{\mathbb {R} }f(t)e^{-i\omega t}dt$ is an isomorphism mapping integrable functions with pointwise multiplication to integrable functions with convolution multiplication.

Exercise: An isomorphism from a ring to itself is called an automorphism. Prove that the following functions are automorphisms:

1. $f:\mathbb {C} \to \mathbb {C} ,f(a+bi)=a-bi$
2. Define the set $\mathbb {Q} ({\sqrt {2}})=\left\{a+b{\sqrt {2}}|a,b\in \mathbb {Q} \right\}$, and let $g:\mathbb {Q} ({\sqrt {2}})\to \mathbb {Q} ({\sqrt {2}}),g(a+b{\sqrt {2}})=a-b{\sqrt {2}}$

Ideals

Motivation

In Rings we saw that the set of even integers $2\mathbb {Z} \subset \mathbb {Z}$ was a subring of the integers.

We can also see very easily that the integers $\mathbb {Z} \subset \mathbb {Q}$ are a subring of the rational numbers under the usual operations of addition and multiplication.

The even integers, when taken as a subring of the integers have a property that the integers when taken as a subring of the rationals do not. The even integers taken as a subring of the rationals also lack this property.

The property is that the even integers, taken as a subring of the integers, absorb multiplication. Let's call the even integers $I=2\mathbb {Z}$ for ease of notation.

Consider the following: For all $i\in I$, we can see by the definition of $I$ that $i=2k$ for some $k\in \mathbb {Z}$.

For all $a\in \mathbb {Z}$ see that $ai=a(2k)=2ak\in I$.

In Math, regardless of which even integer is chosen, multiplying it by any integer will give us a different even integer.

Definition of an Ideal

Definition: Given a ring $R$, a subset $I\subseteq R$ is said to be a left ideal of $R$ if it absorbs multiplication from the left; that is, if $\forall i\in I,\forall r\in R,ri\in I$.

Definition: Given a ring $R$, a subset $I\subseteq R$ is said to be a right ideal of $R$ if it absorbs multiplication from the right; that is, if $\forall i\in I,\forall r\in R,ir\in I$.

Definition: We define an ideal $I$ to be something that is both a left ideal and a right ideal. We also require that $(I,+)$ is a subgroup of $(R,+)$.

We write $I\triangleleft R$ as shorthand for this.

To verify that a subset of a ring is an ideal, it is only necessary to check that it is closed under subtraction and that it absorbs multiplication; this is because of the subgroup criterion from Abstract Algebra/Group Theory/Subgroup.

Definition: An ideal $I\triangleleft R$ is proper if $I\subsetneq R$.

Definition: An ideal $I\triangleleft R$ is trivial if $I=\{0\}$.

Lemma: An ideal $I$ is proper if and only if $1\notin I$.

Proof: If $1\in I$ then $r=r1\in I$ so $I=R$.

The converse is obvious.

Theorem: In a division ring, the only proper ideal is trivial.

Proof: Suppose we have an ideal in a division with a nonzero element a. Take any element b in our division ring. Then a⁻¹b is in the division ring as well, and aa⁻¹b = b is in the ideal. Therefore, it is not a proper ideal.

Definition: Let S be a nonempty subset of a ring R. Then the ideal generated S is defined to be the smallest ideal in R containing S, which would be the intersection of all such ideals. We can characterize this ideal by the collection of all finite sums

$\left\{\sum _{i=1}^{n}r_{i1}s_{i}r_{i2}|r_{i1},r_{i2}\in R,s_{i}\in S\right\}$

And one can easily verify that this is an ideal, and that all ideals containing S must contain this ideal. If it is commutative, then one can simply characterize it as

$\left\{\sum _{i=1}^{n}r_{i}1s_{i}|r_{i}\in R,s_{i}\in S\right\}$

The ideal generated by a single element a is called a principal ideal. If the ring is commutative, it consists of all elements of the ring of the form ra where r is any element in the ring.

Example: Let $R=\mathbb {Z}$ be the ring of integers. The principal ideal $(n)$ is the subset of $\mathbb {Z}$ consisting of positive and negative multiples of $n$. For example $(2)$ is the subset of even integers. Then one can view the factor ring $\mathbb {Z} /(n)$ simply as the set $\{0,1,\ldots ,n-1\}$ under addition and multiplication modulo $n$.

Operations on Ideals

Given a collection of ideals we can generate other ideals. For instance it is easy to check that the intersection of any family of ideals is again an ideal. We write this simply as $\bigcap _{j\in J}I_{j}$.

Given any set $S\subset R$ we can construct the smallest ideal of $R$ containing $S$ which we denote by $\langle S\rangle$. It is determined by $\langle S\rangle =\bigcap _{S\subset I\triangleleft R}I$, though often we can be more explicit than this.

If $I_{j\in J}$ is a collection of ideals we can determine the sum, written $\sum _{j\in J}I_{j}$, as the smallest ideal containing all the ideals $I_{j}$. One can check explicitly that its elements are finite sums of the form $\sum _{j\in J}x_{j}$.

Finally if $I,J$ are two ideals in $R$ one can determine the ideal-theoretic product as the smallest ideal containing the set-theoretic product $\{ij\mid i\in I,j\in J\}$. Note that the ideal-theoretic product is in general strictly larger than the set-theoretic product, and that it simply consists of finite sums of the form $\sum i_{r}j_{r}$ where $i_{r}\in I\;j_{r}\in J$

Example: Let $(m)$ and $(n)$ the principal ideals in $\mathbb {Z}$ just given. Then one can check explicitly that $(m)\cap (n)=(r)$, where r is the lcm of m and n. Moreover $(m)(n)=(mn)$, and $(m)+(n)=(s)$ where s is the hcf of m and n. Observe that $(m)(n)=(m)\cap (n)$ if and only if s = mn if and only if m and n are co-prime if and only if $(m)+(n)=(1)$.

Homomorphisms and Ideals

Rings, like groups, have factor objects that are kernels of homomorphisms. Let $f:R\to S$ be a ring homomorphism. Let us determine the structure of the kernel of f which is defined to be all elements which map to the identity.

If a and b are in the kernel of f, i.e. $f(a)=f(b)=0$, and r is any element of R, then

$f(a-b)=f(a)-f(b)=0$,

$f(ar)=f(a)f(r)=0$,

$f(ra)=f(r)f(a)=0$.

Therefore $\ker(f)$ is an ideal of R.

Also note that the homomorphism will be a monomorphism i. e. it is injective or one-to-one when the kernel consists only of the identity element.

We also have the following
Theorem: If the only proper ideal of R is the trivial ideal {0}, then if f is a homomorphism from R to S, and it does not map all elements of R to the identity in S, then it is injective.
Proof: The kernel of the homomorphism must be an ideal, and since the only ideals are R and the trivial ideal, one of these two must be the kernel. However, since not all elements of R map to the identity of S, R is not the kernel, so the trivial ideal must be.

Since this condition is satisfied for all division rings, it is true for all division rings.

The construction of factor rings in the next section will prove that there exists a homomorphism with I as its kernel for any ideal I.

Factor Rings

Definition

Given a ring $R$ and an ideal $I\triangleleft R$, since $I$ is a subgroup of the Abelian group $(R,+)$ (and thus a normal subgroup), by the quotient group construction, the quotient group $R/I$ is well-defined and Abelian, where $R$ means the additive group of $R$. The elements of $R/I$ are the cosets $\{r+I\mid r\in R\}$ of $R$. We define multiplication on $R/I$ by $(a+I)(b+I):=ab+I$, for each $a,b\in R$. The Abelian group $R/I$ together with the multiplication defined above is called the quotient ring or factor ring of $R$ modulo $I$.

To show that this is independent of the choice of a and b (or, the operations are well-defined), suppose that a' and b' are elements of the same respective coset. Then a'=a+j and b'=b+k for some element j,k within I. Then a'b'=ab+ak+jb+jk and since ak, jb, and jk are elements of I, a'b' and ab must belong to the same coset, so ab+I=a'b'+I. Obviously the cosets form a group under addition because of what was proved earlier about factor groups, and furthermore the factor ring forms an abelian group under addition because the ring forms an abelian group under addition. Since the product rs+I is analogous to the multiplication in the ring, it obviously has all the properties of a ring. Furthermore, if the ring is commutative, then the factor ring will also be commutative.

Observe that there is a canonical ring homomorphism $\pi :R\rightarrow R/I$ determined by $\pi (r)=r+I$, called the projection map. We record some properties of this homomorphism in the next section of the isomorphism theorems.

Ring Isomorphism Theorems

We have already proved the isomorphism theorems for groups. Now we can use analogous arguments to prove the isomorphism theorems for rings, substitution the notion of "normal subgroups" with ideals.

Factor Theorem

Let I be an ideal of a ring R, Let $\pi (x)=x+I$ be the usual homomorphism from R to R/I. Now let f be a homomorphism from R to S. Observe that if ${\tilde {\phi }}:R/I\rightarrow S$ is a ring homomorphism, then the composition $\phi ={\tilde {\phi }}\circ \pi :R\rightarrow R/I\rightarrow S$ is a ring homomorphism such that $I\subset \ker {\phi }$ (because $x\in I\Rightarrow \phi (x)={\tilde {\phi }}\circ \pi (x)={\tilde {\phi }}(0_{R/I})=0_{S}$). This characterizes all such morphisms in the following sense

Factor Theorem: Let $\phi :R\rightarrow S$ be a ring homomorphism such that $I\subset \ker {\phi }$. Then there is a unique homomorphism ${\tilde {\phi }}:R/I\rightarrow S$ such that $\phi ={\tilde {\phi }}\circ \pi$. Furthermore, ${\tilde {\phi }}$ is an epimorphism if and only if $\phi$ is an epimorphism, ${\tilde {\phi }}$ is a monomorphism if and only if its kernel is I.

Proof We prove it the same way we did for groups. Define ${\tilde {\phi }}(x+I)$ to be $\phi (x)$. To see that this is well-defined, let a+I=b+I, and so that a-b is an element of I, so that $\phi (a-b)=0_{S}$ so that $\phi (a)=\phi (b)$. Now $\phi$ is a homomorphism, implying that ${\tilde {\phi }}$ is also. The proofs of the additional statements can be carried over from the proofs of the additional statements of the factor theorem from groups.

First Isomorphism Theorem

Let R be a ring, and let f be a homomorphism from R to S with kernel K. Then the image of f is isomorphic to R/K.

Proof
Using the factor theorem, we can find a homomorphism from R/K to S, and since the kernel is the same as the ideal used in forming the quotient group, and since the f is an epimorphism over its image, this homomorphism is an isomorphism.

Second Isomorphism Theorem

Let R be a ring, let I be an ideal, and let S be a subring.

1. S+I, the set of all s+i with s within S and i within I, is a subring of R.
2. I is an ideal of S+I.
3. The intersection of S and I is an ideal of S.
4. (S+I)/I is isomorphic to $S/(S\cap I)$.

Proof

1. It can be verified that it contains 1, and is closed under multiplication.
2. Of course, since I is an ideal of R, then it must be an ideal under any subring.
3. From a similar argument for groups, it can only contain elements of I, but restricted to S, so it must be an ideal of S.
4. Let $f:R\rightarrow R/I$ be a function restricted to the domain S, and define $f(x)=x+I$. It is obvious that its kernel is $S\cap I$ and that its image is (S+I)/I.

Third Isomorphism Theorem

Let I be an ideal of a ring R, and let J be an ideal of the same ring R that contains I. J/I is an ideal of R/I, and R/J is isomorphic to (R/I)/(J/I).

Proof Define the function $f:R/I\rightarrow R/J$ to be $f(a+I)=a+J$ which is well-defined because since I is an ideal that is within J. This is also obviously a homomorphism. Its kernel is all elements that map onto J, and is thus all a+I such that a is within J, or J/I. Moreover, its image is R/J, and so we can use the first isomorphism theorem to prove the result.

Correspondence Theorem

Let I be an ideal of a ring R. Define the function $\pi$ to map the set of rings and ideals containing I to the set of rings and ideals of R/I, where $\pi (X)$ = the set of all cosets x+I where x is an element of X. This function is one-to-one, and the image of rings or ideals containing I are rings or ideals within R/I.

Proof Define the function f from rings or ideals containing I to the rings or ideals of R/I, by f(A)=A/I. We have already proved the correspondence for addition because rings form an abelian group under addition. Thus, we need only to check for multiplication. Suppose S is a subring of R containing I. S/I is obviously closed under addition and subtraction. For multiplication, suppose that x and y are elements of S. Then (x+I)(y+I)=xy+I which is also an element of S/I, proving that it is closed under multiplication. The identity 1 is within S, and we have it that 1+I is also within S/I. Thus, S/I is a subring of R/I. Now suppose that S/I is a subring of R/I. Then it is also obvious that S is closed under addition and subtraction and multiplication, proving that S is a subring of R. Now suppose that J is an ideal of R containing I. Then by the third isomorphism theorem, J/I is an ideal of R/I. Now suppose that J/I is an ideal of R/I. Let r be any element of R, and let j be any element of J. Then since J/I is an ideal of R/I, (r+I)(j+I)=rj+I must be an element of J/I. This indicates that rj must be an element of J, proving that J is an ideal of R.

Chinese Remainder Theorem

Definitions

Definition: Two elements $a,b$ are said to be congruent in an ideal $I$ if and only if they belong to the same coset in R/I. This is true when a-b is within I. Write $a=b{\bmod {I}}$ to mean that $a$ is congruent to $b$ modulo $I$.

Lemma: Given an ideal $I\subseteq R$, a subset of a ring $R$, the congruence class $[r]$ modulo $I$ of an element $r\in R$ is $[0]$ if and only if $r\in I$. To see this, simply note that $a=b{\bmod {I}}$ means $a-b\in I$; plugging in gives $r-0\in I$.

Definition: Two natural numbers are relatively prime when ax+by=1 for integers x and y. We do the same for rings - two ideals I and J are relatively prime when ai+bj=1 for ring elements a, b, and for an element i within I and an element j within J. In other words, two ideals are relatively prime if their sum contains the identity element i. e. if I+J is the whole ring R.

We will now prove the

Chinese Remainder Theorem

Let R be a ring, and let $I_{n}$ be n pairwise (i. e. when considering any two pairs) relatively prime ideals.

1. Let a be a number from 1 to n. There exists an element r within R that is within all ideals $I_{n}$ such that $n\neq a$, and such that $r=1{\bmod {I_{a}}}$
2. Let $r_{1},r_{2},...,r_{n}$ be elements of R. Then there exists an element r within R such that $r=r_{i}{\bmod {I_{i}}}$ for all i=1,2,3,...,n.
3. Let I be the intersection of the ideals. Another element of R, s satisfies $s=r_{i}{\bmod {I_{i}}}$ for all i=1,2,3,...,n if and only if $r=s{\bmod {I}}$.
4. R/I is isomorphic to the product ring $\Pi _{i=1}^{n}R/I_{i}$

Proof

1. Since $I_{1}$ and $I_{i}$ (i>1) are relatively prime, there will exist an elements $b_{i}\in I_{1}$ and $c_{i}\in I_{i}$ (i>1) such that $b_{i}+c_{i}=1$. This implies that $\Pi _{i=2}^{n}(b_{i}+c_{i})=1$. Now we expand this product on the left side. All terms of the product other than $c_{2}c_{3}c_{4}...c_{n}$ belong to $I_{1}$ while $c_{2}c_{3}c_{4}...c_{n}$ itself belongs the set S of all finite sums of products $x_{2}x_{3}x_{4}...x_{n}$ with $x_{i}\in I_{i}$. Thus, it can be written in the form b+a=1, where b is an element of $I_{1}$, and where a is an element of S. Then $a\equiv 1{\pmod {I_{1}}}$ and $a\equiv 0{\pmod {I_{i}}}$ for i>1.

Prime and Maximal Ideals

There are two important classes of ideals in a ring - Prime and Maximal.

Definition: An ideal $I\triangleleft R$ is prime if it satisfies:

for any ideals A and B such that AB is a subset of I , implies A is in I or B is in I.

Definition: An ideal $I\triangleleft R$ is maximal if it is proper (i.e. $I\subsetneq R$ and it satisfies:

$I\subset J\triangleleft R\implies I=J{\text{ or }}J=R$

That is, there are no proper ideals between $I$ and $R$.

The following Lemma is important for many results, and it makes essential use of Zorn's Lemma (or equivalently the Axiom of Choice)

Lemma: Every non-invertible element of a ring is contained in some maximal ideal

Proof: Suppose $x$ is the non-invertible element. Then the first observation is that $(x)$ is a proper ideal, for if $(x)=R$, then in particular $1\in (x)$ so $1=ax$ contradiction the assumption. Let ${\mathcal {S}}$ be the set of proper ideals in $R$ containing $x$ ordered by inclusion. The first observation implies that ${\mathcal {S}}$ is non-empty, so to apply Zorn's Lemma we need only show that every increasing set of ideals contains an upper-bound. Suppose $\{I_{j}\}_{j}$ is such an increasing set, then the least upper bound is $\sum _{j\in j}I_{j}$ as this is the smallest ideal containing each ideal. If one checks that the union $\cup _{j\in J}I_{j}$ is an ideal, then this must be $\sum _{j\in J}I_{j}$. To show it's proper, we need only show $1\notin \cup _{j\in J}I_{j}$ for all $j$. But this follows precisely because each $I_{j}$ is proper.

Therefore by Zorn's Lemma there is a maximal element $J$ of ${\mathcal {S}}$. It is clearly maximal for if $J'$ were any ideal satisfying $J\subset J^{\prime }\subsetneq R$ then $J^{\prime }$ would be an element of ${\mathcal {S}}$, and by maximality of $J$ we would have $J^{\prime }\subset J$ whence $J=J^{\prime }$.

Properties of rings may be naturally restated in terms of the ideal structure. For instance

Proposition: A commutative ring $R$ is an Integral Domain if and only if $(0)$ is a prime ideal.

Proof: This follows simply because $x=0\iff x\in (0)$.

This explains why an Integral Domain is also referred to as a Prime Ring. Similarly, we may give a necessary and sufficient condition for a ring to be a field :

Proposition: A commutative ring $R$ is a Field if and only if $(0)$ is a maximal ideal (that is there are no proper ideals)

Proof: We only need to show that every element $0\neq x\in R$ is invertible. Suppose not then by Lemma ... $x$ is contained in some (proper) maximal ideal, a contradiction.

Corollary: An ideal $I\triangleleft R$ is maximal if and only if $R/I$ is a field.

Proof: By the previous Proposition we know $R/I$ is a field if and only if its only proper ideal is $(0)$. By the correspondence theorem (...) this happens if and only if there are no proper ideals containing $I$.

Corollary: The kernel of a homomorphism f from R to S is a maximal ideal when S is a field. The proof of this follows from the first isomorphism theorem because S is isomorphic to R/ker f.

It's also clear that

Lemma: An ideal $I\triangleleft R$ is prime if and only if $R/I$ is an integral domain.

Proof: Write ${\bar {x}}$ for the element of $R/I$ corresponding to the equivalence class $[x]$. Clearly every element of $R/I$ can be written in this form.

$\Rightarrow )$ ${\bar {xy}}=0\iff xy\in I\iff x\in I{\text{ or }}y\in I\iff {\bar {x}}=0{\text{ or }}{\bar {y}}=0$ where the second equivalence follows directly because $I$ is prime.

$\Leftarrow )$ This follows in exactly the same way.

Corollary: The kernel of a homomorphism f from R to S is a prime ideal when S is an integral domain. The proof of this follows from the first isomorphism theorem because S is isomorphic to R/ker f.

Lemma: A maximal ideal is also prime.

Proof: Suppose $I\triangleleft R$ is a maximal ideal, and $xy\in I$. Suppose further that $x\notin I$. Then the ideal $I+(x)$ is an ideal containing $I$ and $x$, so is strictly larger than $I$. By maximality $I+(x)=R\ni 1$. So $1=i+rx\implies y=iy+rxy\in I$.
Alternatively, we can use the above two results, and the fact that all fields are integral domains to prove this.

Glossary

Please see the extensive Wikipedia:Glossary of ring theory.

Integral domains

Integral Domains

Motivation: The concept of divisibility is central to the study of ring theory. Integral domains are a useful tool for studying the conditions under which concepts like divisibility and unique factorization are well-behaved. In fact, they are very important for polynomial rings as well.

The integral domain was already defined before on the page on rings. We provide the definition again for reference.

Definition An integral domain is a commutative ring $R$ with $1_{R}\neq 0_{R}$ such that for all $a,b\in R$, the statement $ab=0$ implies either $a=0$ or $b=0$.

An equivalent definition is as follows:

Definition Given a ring $R$, a zero-divisor is an element $a\in R$ such that $\exists x\in R,x\neq 0$ such that $a*x=0_{R}$.

Definition An integral domain is a commutative ring $R$ with $1_{R}\neq 0_{R}$ and with no non-zero zero-divisors.

Remark An integral domain has a useful cancellation property: Let $R$ be an integral domain and let $a,b,c\in R$ with $a\neq 0$. Then $ab=ac$ implies $b=c$. For this reason an integral domain is sometimes called a cancellation ring.

Examples:

1. The set $\mathbb {Z}$ of integers under addition and multiplication is an integral domain. However, it is not a field since the element $2\in {Z}$ has no multiplicative inverse.
2. The set trivial ring {0} is not an integral domain since it does not satisfy $0\neq 1$.
3. The set $\mathbb {Z} _{6}$ of congruence classes of the integers modulo 6 is not an integral domain because $[2]*[3]=[0]$ in $\mathbb {Z} _{6}$.

Theorem: Any field $F$ is an integral domain.

Proof: Suppose that $F$ is a field and let $a\in F,a\neq 0$. If $ax=0$ for some $x$ in $F$, then multiply by $a^{-1}$ to see that $ax=0\Rightarrow a^{-1}(ax)=a^{-1}0\Rightarrow 1x=0\Rightarrow x=0$. $F$ cannot, therefore, contain any zero divisors. Thus, $F$ is an integral domain.$\square$

Definition If $R$ is a ring, then the set of polynomials in powers of $x$ with coefficients from $R$ is also a ring, called the polynomial ring of $R$ and written $R[x]$. Each such polynomial is a finite sum of terms, each term being of the form $rx^{n}$ where $r\in R$ and $x^{n}$ represents the $n$-th power of $x$. The leading term of a polynomial is defined as that term of the polynomial which contains the highest power of $x$ in the polynomial.

Remark A polynomial equals $0$ if and only if each of its coefficients equals $0$.

Theorem: Let $R$ be a commutative ring and let $R[x]$ be the ring of polynomials in powers of $x$ whose coefficients are elements of $R$. Then $R[x]$ is an integral domain if and only if $R$ is.

Proof If commutative ring $R$ is not an integral domain, it contains two non-zero elements $a$ and $b$ such that $ab=0$. Then the polynomials $ax$ and $bx$ are non-zero elements of $R[x]$ and $axbx=abxx=0xx=0$. Thus if $R$ is not an integral domain, neither is $R[x]$.

Now let $R$ be an integral domain and let $A$ and $B$ be polynomials in $R[x]$. If the polynomials are both non-zero, then each one has a non-zero leading term, call them $ax^{m}$ and $bx^{n}$. That these are the leading terms of polynomials $A$ and $B$ means that the leading term of the product $AB$ of these polynomials is $abx^{m+n}$. Since $R$ is an integral domain and $a,b\in R$, $ab\neq 0$. This means, by the Remark above, that the product $AB$ is not zero either. This means that $R[x]$ is an integral domain.

Unique Factorization Domains, Principal Ideal Domains, and Euclidean Domains

Unique Factorization Domains, Principal Ideal Domains, and Euclidean Domains are ideas that work only on integral domains.

Some definitions

• Two ring elements a and b are associates if a=ub for some unit u, we write a~b
• A nonzero nonunit a is irreducible if a=bc (b,c in domain)=>a~b or a~c.
• a divides b if b=ar for some r within R. When this happens, we write a|b.
• A nonzero nonunit is prime when a|bc implies that a|b or a|c.

Theorem: If a is prime, then a is irreducible.

Let a be prime, and let a=bc, so that either a|b or a|c. Without loss of generality, assume that a|b, so that b=ad for some element d. Then you can factor a=bc into a=adc, implying that cd=1, or that c is a unit.

Now that we have proven that all prime elements are irreducible, is the converse true? The answer to that is no, for we can easily obtain counterexamples to it. However, we will prove a sufficient and necessary condition for all irreducible elements to be prime.

Unique Factorization Domains

Definition: Let R be an integral domain. If the following two conditions hold:

1. If a is nonzero, then a=up₁p₂...p_n where u is a unit, and p_i are irreducible.
2. Let a=uq₁q₂...q_m be another factorization of irreducibles. Then n = m and after a suitable re-ordering, each p_i and q_i are associates.

Then we call (the integral domain) R a unique factorization domain (UFD).

The converse to the above theorem holds true in a UFD.

Theorem: In a UFD, all irreducibles are prime.

Proof
Let a|bc, where a is irreducible. Then ad=bc for some element d. Taking the factorization, a = ud₁d₂...d_l = vb₁b₂...b_mwc₁c₂...c_n = bc where u, v, and w are units. Because it is a UFD, a must be an associate of some b_i or c_i, implying that a|b or a|c.

The following theorem provides a sufficient and necessary condition for an integral domain R to be an integral domain.

Theorem:

1. Let R be a UFD. R satisfies the following ascending chain condition on principal ideals: let $a_{1},a_{2},a_{3},...$ be a sequence of elements of R such that the principal ideals $(a_{1}),(a_{2}),(a_{3}),...$ satisfy the condition that $(a_{1})\subseteq (a_{2})\subseteq (a_{3})\subseteq ,...$. Then there exists an N such that for all n>N, all the $(a_{n})$ are the same.
2. If an integral domain R satisfies the ascending chain condition, then every nonzero element can be factored into irreducible elements, meaning that it satisfies the first condition for being a UFD.
3. If, in addition to satisfying the ascending chain condition, all irreducible elements are prime, then the integral domain is a UFD.

Proof

1. Consider a sequence $a_{1},a_{2},a_{3},...$ of elements of R such that $(a_{1})\subseteq (a_{2})\subseteq (a_{3})\subseteq ,...$. Then obviously $a_{n+1}|a_{n}$ for all natural numbers n, since $a_{n}\in (a_{n+1})$. Then due to unique factorization, all the factors of $a_{n+1}$ are associates of the factors $a_{n}$, counting multiplicity of factors. Therefore, the number of non-unit factors is a decreasing sequence on the whole numbers. However, $a_{1}$ has finitely many factors, so there is an N such that for all n>N, all the factors are $a_{n}$ associates, meaning that all the $(a_{n})$ are also the same.
2. Clearly any nonzero irreducible $a_{1}$ can be factored into irreducibles, which is itself. Otherwise, let $a_{1}=a_{2}b_{2}$ be a product of nonunits. If this is not a product of irreducibles, then suppose that one of them is not irreducible, say $a_{2}$. Then obviously $a_{2}|a_{1}$ so the principal ideals satisfy the relations $(a_{1})\subseteq (a_{2})$. We can factor $a_{2}$ in the same way, to obtain $a_{2}=a_{3}b_{3}$ as a product of nonunits. Thus, if $a_{1}$ cannot be factored into irreducibles, we can get an increasing chain $(a_{1})\subseteq (a_{2})\subseteq (a_{3})\subseteq ...$ of principal ideals, meaning that it does not satisfy the ascending chain condition.
3. Let $a=sp_{1}p_{2}p_{3}...p_{n}=rq_{1}q_{2}q_{3}...q_{n}$ where r and s are units and each $p_{i}$ and $q_{i}$ are irreducible, and thus prime. Since $p_{1}$ divides a, it divides one of the factors, and after suitably re-arranging the second factorization, $p_{1}$ can divide $q_{1}$. However, $q_{1}$ is irreducible, so they must be associates, and thus can be factored out and replaced by a unit. We can continue this process until there are no factors left, at which point we conclude that all the factors are associates.

Principal Ideal Domains

Definition: a principal ideal domain (PID) is an integral domain such that every ideal can be generated by a single element (i. e. every ideal is a principal ideal).

Theorem: All PIDs are UFDs.

Proof:
Suppose we have an ascending chain of principal ideals $(a_{1})\subseteq (a_{2})\subseteq ...$ and let I be the union $I=\bigcup _{i=1}^{\infty }(a_{i})$. Obviously I is an ideal, and is a principal ideal because it is in a PID. Therefore, it is generated by a single element, $I=(a)$. Since $a\in I$, $a\in (a_{N})$ for some N. Then if $i\geq N$, then we have $(a)=(a_{N})$, so it satisfies the ascending chain condition of principal ideals.

Let an element $a$ be irreducible. If $1\in (a)$, then $a$ would be a unit, so (a) must be a proper ideal. If there is no maximal proper ideal containing (a), then the ascending chain condition would not be satisfied, so we can conclude that there is a maximal ideal proper ideal I containing (a) (Note: This does not require the Zorn's lemma or axiom of choice, since we did not use the theorem on maximal ideals). This ideal must be a principal ideal (b), but since $a\in (b)$, b|a, and since $a$ is irreducible, b must either be a unit or an associate of a. Since (b) is a proper ideal, b must not be a unit, so it must be an associate of $a$. Therefore, (a)=(b), so (a) is maximal. However, all maximal ideals are clearly prime, so (a) is a prime ideal, which implies that $a$ is prime.

Theorem: A UFD is a PID if and only if every nontrivial prime ideal is maximal.

Proof:
Suppose R is a PID, so that consequently, it is a UFD. Let (a) be an ideal of R, which in turn must be contained in a maximal proper ideal (b) due to the ascending chain condition (Note: again, this does not make use of Zorn's lemma). Since $a\in (b)$, b|a. Since $a$ is irreducible, b must either be a unit or an associate of $a$. However, since (b) is a proper ideal, it must not be a unit, so it must be an associate of $a$. Therefore, (a)=(b), so (a) is maximal. Conversely,

Euclidean Domains

Definition: An integral domain R is a Euclidean domain (ED) if there is a function f from the nonzero elements of R to the whole numbers such that for any element $a\in R$ and any nonzero element b, that a=bq+r for some $q,r\in R$ and such that f(r)<f(b) or such that r=0.

Note: In an ED, the Euclidean algorithm to find the greatest common divisor is applicable.

Theorem: All EDs are PIDs.

Proof:
Suppose we have an ideal of R. If it contains only 0, then it is principal. Otherwise, it contains elements other than 0. Then f(I), the image of I under f, is a nonempty set of nonnegative integers. Choose the minimum x of this set, and consider an element b within I which mapped to this x. Let a be another element of I, and there exists $q,r\in R$ such that a=qb+r and such that either f(r)<f(b) or r=0. Since both a and b belong to I, r must also belong to I since r=a-qb. However, f(b) is the minimum, so it must be less than or equal to f(r). Thus, r must be 0, so a=qb, proving that b is the generator of the principal ideal (b).

Fraction Fields

We know from experience that we arrive at the idea of fractions by merely considering the idea of the quotient of two integers. The motivation behind this is simply to arrive at a multiplicative inverse for every non-zero element. Thus, we can consider an integral domain R and construct its field of fractions. However, we can also try to make this work for any commutative ring, even if it has zero divisors other than 0. There is a slight alteration required because we cannot define ${\frac {a}{b}}{\frac {c}{d}}$ when bd=0. Thus, we must place restrictions in case b and d are zero divisors in the case of multiplication. In this case, it is called the localization of a ring.

Definitions

A multiplicative subset of a commutative ring R is a subset that does not contain 0, does contain 1, and is closed under multiplication. Some examples of multiplicative sets are the set of nonzero elements of an integral domain, the set of elements of a commutative ring that are not zero divisors, and R\P where P is a prime ideal of the commutative ring R.

Let S be a multiplicative subset. We will consider the Cartesian product R×S. Define the equivalence relation on this product: (a,b)~(c,d) whenever there exists an s such that s(ad-bc)=0.

If it is an integral domain, then (a,b) could be regarded as a/b. Now to check that this is an equivalence relation, it is obvious that it is reflexive and symmetric. To prove that it is transitive, let (a,b)~(c,d) and let (c,d)~(e,f). Then there are elements s and t within S such that s(ad-bc)=0 and such that t(cf-de)=0. This implies that stfad-stfbc=0 and that sbtcf-sbtde=0. Adding the two, we get stfad-sbtde=0, or std(af-be)=0, implying that (a,b)~(e,f).

We can thus use these equivalence classes to define the fraction: ${\frac {a}{b}}$ is the equivalence class containing (a,b).

Now we set this to be a ring. First, we define addition to be ${\frac {a}{b}}+{\frac {c}{d}}={\frac {ad+bc}{bd}}$ and multiplication to be ${\frac {a}{b}}\cdot {\frac {c}{d}}={\frac {ac}{bd}}$. The additive identity is ${\frac {0}{1}}$ and the additive inverse is ${\frac {-a}{b}}$. The multiplicative identity is simply ${\frac {1}{1}}$.

Now we prove below that it is indeed a ring:

Theorem

The set of fractions with addition and multiplication as defined is a commutative ring, and if R is an integral domain, then the fractions are also. And if additionally S is R\{0}, then the set of fractions is a field.

Proof

First, we note that

1. $({\frac {a}{b}}+{\frac {c}{d}})+{\frac {e}{f}}={\frac {ad+bc}{bd}}+{\frac {e}{f}}={\frac {(ad+bc)f+bde}{bdf}}={\frac {adf+b(cf+de)}{bdf}}={\frac {a}{b}}+{\frac {cf+de}{df}}={\frac {a}{b}}+({\frac {c}{d}}+{\frac {e}{f}})$
2. ${\frac {a}{b}}+{\frac {0}{1}}={\frac {a\cdot 1+b\cdot 0}{b\cdot 1}}={\frac {a}{b}}$
3. $\forall c\in S:1_{R}(0\cdot 1-0\cdot c)=0\Rightarrow {\frac {0}{1}}={\frac {0}{c}}(*)$ and therefore ${\frac {a}{b}}+{\frac {-a}{b}}={\frac {ab+b(-a)}{bb}}={\frac {0}{bb}}={\frac {0}{1}}$

, from which follows that $(R\times S,+)$ is a group.

It is abelian because of the definition of the sum in S and R is commutative.

Furthermore, $(R\times S,\cdot )$ is a monoid because

1. ${\frac {1}{1}}\cdot {\frac {a}{b}}={\frac {1a}{1b}}={\frac {a}{b}}$
2. and $({\frac {a}{b}}\cdot {\frac {c}{d}})\cdot {\frac {e}{f}}={\frac {ace}{bdf}}={\frac {a}{b}}\cdot ({\frac {c}{d}}\cdot {\frac {e}{f}})$, where two (not difficult) intermediate steps are left to the reader.

And, also the distributive laws hold, because

${\frac {a}{b}}\left({\frac {c}{d}}+{\frac {e}{f}}\right)=\left({\frac {c}{d}}+{\frac {e}{f}}\right){\frac {a}{b}}={\frac {acf+ade}{bdf}}$ and

${\frac {acf+ade}{bdf}}={\frac {acbf+adbe}{bdfb}}={\frac {ac}{bd}}+{\frac {ae}{bf}}$

, which shows that we have indeed found a ring.

The ring is commutative because of the definition of the product in S R is commutative.

Let now R be an integral domain, and let ${\frac {a}{b}},{\frac {c}{d}}\in S$. Then, because of $(*)$ and since $bd\in S$, ${\frac {a}{b}}\cdot {\frac {c}{d}}=0\Leftrightarrow {\frac {ac}{bd}}=0\Leftrightarrow {\frac {ac}{bd}}={\frac {0}{bd}}\Leftrightarrow \exists s\in S:s(ac\cdot bd-0\cdot bd)=sacbd=0$. But since R was assumed to be an integral domain, and $s,b,d\neq 0$ since $s,b,d\in S$, the last statement is exactly equivalent to $\exists s\in S:a=0\vee c=0$, which is in turn equivalent to $\exists s\in S:sab=s(ab-0b)=0\vee \exists s\in S:scd=s(cd-0d)=0$, and this is equivalent to ${\frac {a}{b}}=0\vee {\frac {c}{d}}=0$, which shows that the fraction set is an integral domain if R is one.

Let's assume now that S = R \ {0}, and let ${\frac {a}{b}}\neq 0\Leftrightarrow a\neq 0$, where the last equivalence is due to (*) and ${\frac {a}{b}}=0\Leftrightarrow \exists s\in S:s(a1-b0)=as1=as=0\Leftrightarrow a=0$, where the last equivalence is in turn due to the fact that R is an integral domain and S does not contain zero. Then $ab\neq 0$ due to the fact that R is an integral domain, and therefore $ab\in S$ since S = R \ {0}, and ${\frac {a}{b}}\cdot {\frac {b}{a}}={\frac {ab}{ab}}$. But since $\forall s\in S:s(ab1-ba1)=0$, we have ${\frac {ab}{ab}}=1$ and ${\frac {a}{b}}\cdot {\frac {b}{a}}=1$ and therefore, by noting that we have assumed R to be commutative, we have that every element of R\{0} is invertible.

From this follows that the set of fractions is indeed a field, because we have already checked all field axioms, QED.

Polynomial Rings

The degree of a polynomial $a_{0}+a_{1}X+...+a_{n}X^{n}$ is defined to be $n$. If $R$ is a field, and $f$ and $g$ are polynomials of $R[X]$, then we can divide $f$ by $g$ to get $f=gq+r$. However, we can also do this for any arbitrary ring if the leading coefficient of $g$ is 1.

Take real numbers R for the ring and adjoin two indeterminants X and Y. The free algebra R<X,Y> over R is the collection of sums and products involving X, Y, and real numbers. The polynomial ring R[X,Y] is the algebra reduced by XY=YX, commutativity of the two indeterminants. In terms of quotient rings, with ideal generated by XY−YX, R[X,Y] = R<X,Y>/(XY−YX). The polynomial ring is central to commutative algebra, such as in the discussion of bibinarions and tessarines to follow.

In non-commutative algebra, the anti-commutative property XY=−YX is illustrated in the quaternions. So-called "imaginary units" correspond to irreducible binomials XX+1 and YY+1. The elements of the quotient algebra R<X,Y>/(XY+YX, XX+1, YY+1) multiply as quaternions.

Exercises: What are the common names of these quotients ?

• Polynomial quotient R[X]/(XX−1)
• Free algebra quotient R<X,Y>/(XY+YX, XX+1, YY−1).

Application: Bibinarions & Tessarines

Commutative four-dimensional hypercomplex number systems were put forward in the nineteenth century. James Cockle presented the tessarines and Corrado Segre the bicomplex numbers, called Bibinarions in the study of Associative Composition Algebra. The isomorphism of these systems can be demonstrated through quotients of polynomial rings:

Consider the polynomial ring R[X,Y], where XY = YX. The ideal $A=(X^{2}+1,\ Y^{2}-1)$ then provides a quotient ring representing tessarines. In this quotient ring approach, elements of the tessarines correspond to cosets with respect to the ideal A. Similarly, the ideal $B=(X^{2}+1,\ Y^{2}+1)$ produces a quotient representing bicomplex numbers.

A generalization of this approach uses the free algebra R⟨X,Y⟩ in two non-commuting indeterminates X and Y. Consider these three second degree polynomials $X^{2}+1,\ Y^{2}-1,\ XY-YX$. Let A be the ideal generated by them. Then the quotient ring R⟨X,Y⟩/A is isomorphic to the ring of tessarines.

To see that $(XY)^{2}+1\in A$  note that

$XY^{2}X=X(Y^{2}-1)X+(X^{2}+1)-1,$ so that

$XY^{2}X+1=X(Y^{2}-1)X+(X^{2}+1)\in A.$ But then

$XY(XY-YX)+XY^{2}X+1\in A.$ as required.

Now consider the alternative ideal B generated by $X^{2}+1,\ Y^{2}+1,\ XY-YX$. In this case one can prove $(XY)^{2}-1\in B$. The ring isomorphism R⟨X,Y⟩/A ≅ R⟨X,Y⟩/B involves a change of basis exchanging $Y\leftrightarrow XY$.

Alternatively, suppose the field C of ordinary complex numbers is presumed given, and C[X] is the ring of polynomials in X with complex coefficients. Then the quotient C[X]/(X² + 1) is another presentation of bicomplex numbers.

Modules

Motivation

Let G be an abelian group under addition. We can define a sort of multiplication on G by elements of $\mathbb {Z}$ by writing $ng=\underbrace {g+g+\cdots +g} _{n}$ for $n\in \mathbb {Z} ^{+}$ and $g\in G$. We can extend this to the case where n is negative by writing $(-n)g=\underbrace {-g-g-\cdots -g} _{n}$. We would, however, like to be able to define a sort of multiplication of a group by an arbitrary ring.

Definition

Definition 1 (Module)

Let R be a ring and M an abelian group. We call M a left R-module if there is a function $R\times M\to M\,:\,(r,m)\mapsto rm$, called a scalar multiplication, satisfying

1. $(r+s)m=rm+sm$,
2. $r(m+n)=rm+rn$, and
3. $(rs)m=r(sm)$

for all $r,s\in R,\ m,n\in G$.

We call R the ring of scalars of M.

Note: We can also define a right R-module analogously by using a function $M\times R\to M\,:\,(m,r)\mapsto mr$. In particular the third property then reads:

$m(rs)=(mr)s$

Note that the two notions coincide if R is a commutative ring, and in this case we can simply say that M is an R-module.

Definition 2: Given any ring R, we can define it's opposite ring, $R^{\mathrm {op} }$, having the same elements and addition operation as R, but opposite multiplication. Their multiplication rules are related by $r\cdot s=sr$. In contrast to group theory, there is no reason in general for a ring to be isomorphic to its opposite ring.

The observant reader will have noticed that the scalar multiplication in a left R-module M is simply a ring homomorphism $\phi \,:\,R\to \mathrm {End} (M)$ such that $rm=\phi (r)(m)$ for all $r\in R\,,\,m\in M$. We leave it as an exercise to verify that the scalar multiplication in a right R-module is a ring homomorphism $\phi ^{\prime }\,:\,R^{\mathrm {op} }\to \mathrm {End} (M)$. Thus a right R-module is simply a left R^op-module. As a consequence of this, all the results we will formulate for left R-modules are automatically true for right R-modules as well. There are no assumptions that the module is unital, namely that 1m = m for all m in M.

Examples of Modules

1. Any ring R is trivially an R-module over itself. More interestingly, any left ideal I of R is also a left R-module with the obvious scalar multiplication. In addition, if I is a two-sided ideal of R, then the quotient ring $R/I$ is an R-module with the induced scalar multiplication $r(s+I)=rs+I\,,\,(s+I)r=sr+I$.
2. If R is a ring, then the set $M_{n,m}(R)$ of $n\times m$ matrices with entries in R is an R-module under componentwise addition and scalar multiplication. More generally, for any set X, the set $R^{X}$ of function from X to R, with or without finite support, is an R-module in an obvious way.
3. The k-modules over a field k are simply the k-vector spaces.
4. As was shown in the introduction of this chapter, any abelian group is a $\mathbb {Z}$-module in a natural way. ("Natural" here has a rigorous mathematical meaning which will be explained later.
5. Let S be a subring of a ring R. Then R is an S-module in a natural way. We can extend this as follows. Let S,R be rings and $\phi \,:\,S\to R$ a ring homomorphism. Then R is an S-module with scalar multiplication $sr=\phi (s)r$ and $rs=r\phi (s)$ for all $s\in S\,,\,r\in R$.
6. Any matrix ring of a ring R is a R-module under componentwise scalar multiplication.
7. If S is a subring of a ring R, then any left R-module is also a left S-module with the restricted scalar multiplication. We will treat this more generally later.

Submodules

Definition 3: (Submodule)

Given a left $R$-module $M$ a submodule of $M$ is a subset $N\subseteq M$ satisfying

1. N is a subgroup of M, and
2. for all $r\in R$ and all $n\in N$ we have $rn\in N$.

The second condition above states that submodules are closed under left multiplication by elements of $R$; it is implicit that they inherit their multiplication from their containing module; $R\times N\to N$ must be the restriction of $R\times M\to M$.

Example 4: Any module M is a submodule of itself, called the improper submodule, and the zero submodule consisting only of the additive identity of M, called the trivial submodule.

Example 5: A left ideal I is a submodule of R viewed as an S-module, where S is any (not necessarily proper) subring of R.

Lemma 6: Let M be a left R-module. Then the following are equivalent.

i) N is a submodule of M

ii) If $r_{i}\in R$ and $n_{i}\in N$ for all $i\in I=\{1,\dots ,k\}\,,\,k\in \mathbb {N}$, then $\sum _{i\in I}r_{i}n_{i}\in N$.

iii) If $r_{1},r_{2}\in R$ and $n_{1},n_{2}\in N$, then $r_{1}n_{1}+r_{2}n_{2}\in N$.

Proof: i) => iii): $r_{1}n_{1}$ and $r_{2}n_{2}$ are in $N$ by the second property, then $r_{1}n_{1}+r_{2}n_{2}\in N$ by the first property of Definition 3.

iii) => ii): Follows by induction on $k$.

ii) => i): Let $k=2$, $r_{1}=1\,,\,r_{2}=-1$, then for arbitrary $n_{1},n_{2}\in N$ be have $n_{1}-n_{2}\in N$, proving $N$ is a subgroup. Now let $k=1$, then for arbitrary $r_{1},n_{1}\in N$, $r_{1}n_{1}\in N$, proving property 2 in Definition 3. ∎

The lemma gives an alternative characterisation of submodules, and those sets closed under linear combinations of elements.

Analogously to the case of vector spaces, we have ways of creating new subspaces from old ones. The rest of this subsection will be concerned with this.

Lemma 7: Let M be a left R-module, and let N and L be submodules of M. Then $N\cap L$ is a submodule in M, and it is the largest submodule contained in both N in L.

Proof: Let $a,b\in N\cap L$ and $r,s\in R$. Then $ra+sb\in N$ and $ra+sb\in L$ since N and L are submodules, so $ra+sb\in N\cap L$ and $N\cap L$ is a submodule of M. Now, assume that S is a submodule of M contained in N and L. Then any $a\in S$ must be in both N and L and therefore in $N\cap L$ such that $S\subseteq N\cap L$, proving the lemma. ∎

Now, as the reader should expect at this point, given submodules N and L of M, the union $N\cup L$ is in general not a submodule. In fact, we have the following lemma:

Lemma 8: Let M be a left R-module and let N and L be submodules. Then $N\cup L$ is a submodule if and only if $L\subseteq N$ or $N\subseteq L$.

Proof: The left implication is obvious. For the right implication, assume $N\cup L$ is a submodule of M. Then if $n\in N$ and $l\in L$, then $n+l\in N\cup L$, which implies that $n+l\in M$ or $n+l\in L$. Assume without loss of generality that $n+l\in N$. Then, since N is a submodule, we must have $(n+l)-n=l\in N$, proving $L\subseteq N$. ∎

Definition 9: Let M be a left R-module, and let $N_{i}$ be submodules for $1\leq i\leq k\in \mathbb {N}$. Then define their sum, $\sum _{i=1}^{k}N_{i}=\left\{\sum _{j=1}^{k}n_{j}\,:\,n_{j}\in N_{j}\right\}$.

Definition 9 has a straightforward extension to sums over arbitrary index sets. This definition is left for the reader to state. We will only need the finite case in this chapter.

Lemma 10: Let M be a left R-module and let N and L be submodules. Then $N+L$ is a submodule of M, and it is the smallest submodule containing both N and L.

Proof: It is straightforward to see that $N+L$ is a submodule. To see that it is the smallest submodule containing both N and L, let S be a submodule containing both N and L. Then for any $n\in N\subseteq S$ and $l\in L\subseteq S$, we must have $n+l\in S$. But this is the same as saying that $N+L\subseteq S$, proving the lemma. ∎

With Lemma 7 and Lemma 10 established, we can state the main result of this subsection.

Definition 11: Let M be a left R-module. Then let ${\mathcal {S}}(M)$ be the set of submodules ordered by set inclusion.

Lemma 12: Let M be a left R-module. Then ${\mathcal {S}}(M)$ forms a lattice, the join of $N,L\in {\mathcal {S}}(M)$ being given by $N\vee L=N+L$ and their meet by $N\wedge L=N\cap L$.

Proof: Most of the work is already done. All that remains is to check assosiativity, the absorption axioms and the idempotency axioms. The associativity is trivially satisfied, $A\cap (B\cap C)=(A\cap B)\cap C$ and $(A+B)+C=A+(B+C)$ for all $A,B,C\in {\mathcal {S}}(M)$. As for absorption, We have to check $A+(B\cap A)=A$ and $A\cap (A+B)=A$ for all $A,B\in {\mathcal {S}}(M)$, but this is also trivially true. Lastly, we obviously have $A+A=A$ and $A\cap A=A$ for all ${\mathcal {S}}(M)$, so we are done. ∎

Corollary 13: Let M be a left R-module. Then ${\mathcal {S}}(M)$ is a modular lattice.

Note: Recall that ${\mathcal {S}}(M)$ is modular if and only if whenever $A,B,C\in {\mathcal {S}}(M)$ such that $A\subseteq C$, we have $A+(B\cap C)=(A+B)\cap C$.

Proof: Let $a\in A\,,\,b\in B\,,\,c\in C$ such that $a+b=c$. Since $A\subseteq C$, we have $a=c^{\prime }$ for some $c^{\prime }\in C$, such that $b\in C$. Thus $b\in B\cap C$ and $a+b\in A+(B\cap C)$. On the other hand, we have $a+b\in A+B$ and $a+b=c\in C$, so $a+b\in (A+B)\cap C$. ∎

Definition 14: Let M be a left R-module. A submodule N is called maximal if whenever L is a submodule satisfying $N\subseteq L\subseteq M$, then $L=N$ or $L=M$.

Theorem 15: Every submodule of a finitely generated left R-module is contained in a maximal submodule.

Proof: Let N be a submodule, and let $S=\{L\in {\mathcal {S}}(M)\,|\,N\subseteq L\subset M\}$. Then S is a poset under set inclusion. Let $\{U_{1},U_{2},\dots \}$ be a chain in S, and note that $U=U_{1}+U_{2}+\cdots$ is a submodule containing each $U_{i}$, such that U is an upper bound for the chain. Then, since each chain in S has an upper bound, by Zorn's Lemma S has a maximal element, P, say. P is obviously an ideal containing N. By the definition of S, P is also a maximal submodule of M, proving the theorem. ∎

Generating Modules

Given a subset $A$ of a left $R$-module $M$, we define the left submodule generated by $A$ to be the smallest submodule (w.r.t. set containment) of $M$ that contains $A$. It is denoted by $RA$ for a reason which will become clear in a moment.

The existence of such a submodule comes from the fact that an intersection of $R$-modules is again an $R$-module: Consider the set $S$ of all submodules of $M$ containing $A$. Since $M$ contains $A$, we see that $S$ is non-empty. The intersection of the modules in $S$ clearly contains $A$ and is a submodule of $M$. Further, any submodule of $M$ containing $A$ also contains the intersection. Thus $RA=\cap S$.

Assuming that $M$ is unitary, the elements of $RA$ have a simple description;

$RA=\left\{\sum _{i=1}^{n}r_{i}a_{i}\mid n\in \mathbb {N} ,r_{i}\in R,a_{i}\in A\right\}$.

That is, every element of $RA$ can be written as a finite left linear combination of elements of $A$. This equality can be justified by double inclusion: First, any submodule containing $A$ must contain all left $R$-linear combinations of elements of $A$ since modules are closed under addition and left multiplication by elements of $R$. Thus, $RA\supseteq \{\sum _{i=1}^{n}r_{i}a_{i}\mid n\in \mathbb {N} ,r_{i}\in R,a_{i}\in A\}$. Secondly, the set of all such linear combinations forms a submodule of $M$ containing $A$ (use $n=1$ and $r_{1}=1_{R}$) and hence it contains $RA$.

Generating Submodules by Ideals

Consider any ring $R$, left ideal $I\subseteq R$, and left $R$-module $M$. One can think of $I$ as a subring of $R$ (non-unitary when $I\neq R$) and hence $M$ is an $I$-module using the regular multiplication by elements of $R$.

If we consider the set $IM=\{\sum _{i=1}^{n}r_{i}m_{i}\mid n\in \mathbb {N} ,r_{i}\in I,m_{i}\in M\}$ we obtain a submodule of $M$. This follows from our discussion of generated submodules. However, since $I$ is not unitary, it is not necessary that $IM=M$.

Thus, we may consider the quotient module $M/IM$. Clearly this is an $R$-module but it is also an $R/I$ module under the obvious action.

Proposition

Given an $R$-module $M$ and ideal $I$ of $R$, the $R$module $M/IM$ is an $R/I$-module with multiplication $(r+I)(m+IM)=rm+IM$.

proof.

To show that this is well defined, we observe that if $r+I=s+I$ then $r-s\in I$ and hence

$(rm+IM)-(sm+IM)=rm-sm+IM=(r-s)m+IM=0+IM$

since $(r-s)m\in IM$. Thus,

$(r+I)(m+IM)=rm+IM=sm+IM=(s+I)(m+IM)$

which proves that the action of $R/I$ on $M/IM$ is well defined. It follows now that $M/IM$ is an $R/I$-module simply because it is an $R$-module.

Quotient Modules

Recall that any subgroup $N$ of an abelian group $M$ allows one to construct an equivalence relation; for $m,m^{\prime }\in M$,

$m\sim m^{\prime }\iff m-m^{\prime }\in N$.

Cosets of $N$, equivalence classes under the relation above, can then be endowed with a group structure, derived from the original group, and is given the name M/N. The sum of two cosets $m+N=[m]$ and $m^{\prime }+N=[m^{\prime }]$ is simply $(m+m^{\prime })+N=[m+m^{\prime }]$.

Lemma 16 Let M be a left R-module and N be a submodule. Then M/N, defined above, is a left R-module.

Proof: M/N is obviously an abelian group, so we just have to check that it has a well-defined R-action. Let $r\in R$ and $m\in M$. Then we define $r(m+N)=rm+N$. The distributivity and associativity properties of the action are inherited from M, so we just need well-definedness. Let $m,m^{\prime }\in M$ with $m-m^{\prime }\in N$. Then $r(m-m^{\prime }+N)=r(m-m^{\prime })+N=N$ since N is a submodule, and we are done. ∎

Module Homomorphisms

Like all algebraic structures, we can define maps between modules that preserve their algebraic operations.

Definition (Module Homomorphism)

An $R$-module homomorphism $\phi :M\to N$ is a function from $M$ to $N$ satisfying

1. $\phi (m+m')=\phi (m)+\phi (m')$ (it is a group homomorphism), and
2. $\phi (rm)=r\phi (m).$

When a map between two algebraic structures satisfies these two properties then it called an $R$-linear map.

Definition (Kernel, Image)

Given a module homomorphism $\phi :M\to N$ the kernel of $\phi$ is the set

$\ker \phi =\{m\in M\mid \phi (m)=0\}$

and the image of $\phi$ is the set

$\phi (M)=\{n\in N\mid \exists m\in M,\phi (m)=n\}$.

The kernel of $\phi$ is the set of elements in the domain that are sent to zero by $\phi$. In fact, the kernel of any module homomorphism is a submodule of $M$. It is clearly a subgroup, from group theory, and it is also closed under multiplication by elements of $R$: $\phi (rm)=r\phi (m)=r(0)=0$ for $m\in \ker \phi$.

Similarly, one can show that the image of $\phi$ is a submodule of $N$.

Projective line

Projective Line over a Ring

For a ring A, let $A=U\cup N$ be the division of the ring into units U and non-units N, so that $U\cap N=\emptyset .$

Pairs of ring elements a and b are found in A x A. Another pair c and d are related to the first pair when there is a unit u such that ua = c and ub = d. Using the group properties of U, one can show that this relation is an equivalence. The equivalence classes of this relation are the points of the projective line, provided that the pair a, b generates the improper ideal, A itself.

$P(A)=\{[a:b]:aA+bA=A\},$ where [a:b] denotes the equivalence class of (a,b).

Note that when a b = 1, then [a : 1 ] = [1 : b], so for elements of U, exchanging coordinates produces the multiplicative inverse in the opposite component.

The projective line receives two embeddings of A: z → [z : 1] and z → [1 : z]. On embedded U, the exchange in P(A) involves multiplicative inverse, while on embedded N the exchange brings up the identical non-unit in the opposite embedding.

• Lemma: m + n in U implies m − n in U.

proof: am + bn = 1 = am + (−b)(−n) implies m − n is in U.

When A is a commutative ring there is a relation $p\parallel q$ holding for certain pairs p and q in P(A):

• Definition: Points p = [a:b] and q = [c:d] are point parallel when ad − bc is in N, the non-units. (Benz, page 84, note formula error)

This relation is always reflexive and symmetric.

• Exercise: Show that in case A is a field, then $\parallel$ is the equality relation.

For $\parallel$ to be an equivalence, transitivity can be demonstrated for rings which have a unique maximal ideal (known as local rings).

proof: $[a:b]\parallel [c:d]\ \equiv \ ad-bc\in N.$ For instance with m, n in N, [n:1] and [m:1] are parallel but not [n:1] and [1:m]. In A, if the principal ideals [m] and [n] are always the same, then A is a local ring, and vice versa. In this case the parallel relation is transitive.

The ring of dual numbers is an example of a local ring.

Homographies

Definition: For a ring A, M(2,A) represents the 2x2 matrices with entries from A. Using the operations of A, and matrix addition and multiplication, M(2,A) is itself a ring.

The exchange is an example of a homography on P(A) and can be represented by ${\begin{pmatrix}0&1\\1&0\end{pmatrix}}\in M(2,A).$ The action of matrices in M(2,A) represent transformations of P(A). Row pairs on the left and elements of M(2,A) on the right are the two factors in a multiplicative transformation. When the determinant of such a matrix is a unit in the ring, then the matrix has an inverse in M(2,A).

For example, ${\begin{pmatrix}1&1\\-p&-q\end{pmatrix}}$ has determinant p – q. When p and q are in N, and p+q is in N also, then the matrix is singular (has no inverse) and p and q are point-parallel. If the above determinant is a unit, then the matrix is in a homography group on P(A). Looking at the first embedding, it maps [p:1] to zero and [q:1] to infinity. According to Walter Benz, p and q are point-parallel when there is no homography connecting them by a "chain", that is, a projective line P(Q) where A is an algebra over Q. The homography moved p and q to two points common to all projective lines.

The operations of the original ring A are represented by elements of M(2,A) acting on an embedding. The multiplication by unit u corresponds to ${\begin{pmatrix}u&0\\0&1\end{pmatrix}},$ and addition of t corresponds to ${\begin{pmatrix}1&0\\t&1\end{pmatrix}}.$ In addition, M(2,A) contains matrices ${\begin{pmatrix}1&t\\0&1\end{pmatrix}}$ corresponding to addition in the second embedding or "translation at infinity" with respect to the first embedding.

• w:Walter Benz (1973) Vorlesungen über Geometrie der Algebren, §2.1 Projective Gerade über einem Ring, §2.1.2 Die projective Gruppe, §2.1.3 Transitivitätseigenschaften, §2.1.4 Doppelverhaltnisse, Springer and Internet Archive.

Fields

Fields and Homomorphisms

Definition

Definition (Field)

A field $F$ is a commutative unital ring such that every non-zero $x\in F$ has a multiplicative inverse. In other words, for every $x\in F\setminus \{0\}$ there exists some $y\in F\setminus \{0\}$ such that $x\cdot y=1$.

Essentially, a field is a commutative division ring.

Examples

1. $\mathbb {Q} ,\mathbb {R} ,\mathbb {C}$ (rational, real and complex numbers) with standard $+$ and $\cdot$ operations have field structure. These are examples with infinite cardinality.
2. $\mathbb {Z} _{p}$, the integers modulo $p$ where $p$ is a prime, and $+$ and $\cdot$ are mod $p,$ is a family of finite fields.
3. If $F$ is a field, then $F(x)$, the set of rational functions (i.e. quotients of polynomials), with coefficients in $F$ also forms a field.
4. A non-example is $\mathbb {Z} _{n}$ where $n$ is not prime. For example, 2 in $\mathbb {Z} _{4}$ has no multiplicative inverse, hence $\mathbb {Z} _{4}$ is not a field.

Homomorphisms

Definition (Field Homomorphism)

If $E,F$ are fields then $f:E\to F$ is a field homomorphism if

• $f(a+b)=f(a)+f(b)$
• $f(a\cdot b)=f(a)\cdot f(b)$
• $f(1_{E})=1_{F}$

Therefore a field homomorphism is exactly a unital ring homomorphism.

Lemma 4.1.1

Every field homomorphism is injective.

Proof. This is a simple consequence of the ideal structure of fields. Suppose $f:E\to F$ is a field homomorphism. In particular it is a ring homomorphism so we know that ${\rm {ker}}(f)$ is a an ideal of $E$. Since $E$ is a field, it only has trivial ideals so ${\rm {ker}}(f)=\{0\}$ or ${\rm {ker}}(f)=E$. We can eliminate the second case since $f(1_{E})=1_{F}$ so the map cannot be trivial. Therefore we are in the first case which means exactly that $f$ is injective.      $\blacksquare$

The above lemma means that every field homomorphism can also be thought of as an embedding of fields.

As happens so often in mathematics, a map between objects induces further maps between related objects. For example, a continuous map between topological spaces induces a map between the set of closed curves on the spaces and a linear map between vector spaces induces a linear map between the dual spaces (albeit in the opposite direction). In this case, a homomorphism between fields induces a homomorphism between the corresponding ring of polynomials. To be precise, suppose $\varphi :E\to F$ is a field homomorphism. This induces a map $\varphi _{*}:E[x]\to F[x]$ given by$$\varphi _{*}(a_{0}+a_{1}x+\dots a_{n}x^{n})=\varphi (a_{0})+\varphi (a_{1})x+\dots \varphi (a_{n})x^{n}$$

It is easy to see that $\varphi _{*}$ is a (unital) ring homomorphism. Moreover if $\varphi$ is an isomorphism then so is $\varphi _{*}$.

Characteristic of Fields

An important property of fields is their characteristic. We first need to consider the canonical homomorphism $\varphi$ from $\mathbb {Z}$ into a field $F$. Of course this is defined by mapping the unit to the unit. Since $\mathbb {Z}$ is generated by $1$, this is sufficient to define the entire homomorphism. From the First Isomorphism Theorem, we know that $\mathbb {Z} /{\textrm {ker}}(\varphi )\cong \varphi (\mathbb {Z} )\subseteq F$ . In particular, this means that $\varphi (\mathbb {Z} )$ is a subring and even a subfield of $F$ so is an integral domain. Hence ${\textrm {ker}}(\varphi )$ is a prime ideal of $\mathbb {Z}$. There is a unique non-negative integer generating this ideal. We call this integer the characteristic of $F$. Notice by the above argument that the characteristic must be prime if it is non-zero.

Intuitively, the characteristic of a field $F$ is the smallest positive integer $p$, if one exists, such that $$\underbrace {1+\dots +1} _{p{\text{ times}}}=0$$If no such positive integer exists, then $F$ has characteristic 0. So for example, $\mathbb {Z} _{p}$ all have characteristic $p$ while $\mathbb {Q} ,\mathbb {R}$ and $\mathbb {C}$ have characteristic 0.

Sometimes, one calls the image of $\mathbb {Z}$ under the above canonical homomorphism above the prime subfield of $F$. Hence the prime subfield of a finite field is (isomorphic to) $\mathbb {Z} _{p}$ (where $p$ is the characteristic of $F$) and the prime subfield of a field of characteristic 0 is (isomorphic to) $\mathbb {Q}$.

Field Extensions

Definition (Field Extensions)

Let $F$ and $G$ be fields. If $F\subseteq G$ and there is an embedding from $F$ into $G$, then $G$ is a field extension of $F$.

Let $G$ be an extension of $F$. Since we can scale elements of $G$ by elements of $F$ via the multiplication on $G$, $G$ forms a vector space over $F$ (one can verify all the axioms for vector spaces hold). The dimension of this vector space is the degree of the extension, $[G:F]$. If the degree is finite, then $G$ is a finite extension of $F$, and $G$ is of degree $n=[G:F]$ over F.

Examples

• The complex numbers $\mathbb {C}$ are a field extension of the real numbers $\mathbb {R}$. The extension is of degree 2.
• Similarly, one can add the imaginary number $i$ to the field of rational numbers $\mathbb {Q}$ to form $\mathbb {Q} (i)$ the field of Gaussian rationals. This is also a degree 2 extension.
• The real numbers $\mathbb {R}$ form a field extension over $\mathbb {Q}$ but this is not a finite extension since the real numbers do not form a finite dimensional (or even a countably infinite dimensional) vector space over $\mathbb {Q}$.

Algebraic Extensions

Definition (Algebraic Extensions)

Let $K$ be an extension of $F$. Then $\lambda \in K$ is algebraic over $F$ if there exists a non-zero polynomial $f(x)\in F[x]$ such that $f(\lambda )=0$. $K$ is an algebraic extension of $F$ if $K$ is an extension of $F$, such that every element of $K$ is algebraic over $F$.

For example, $\mathbb {Q} ({\sqrt {2}})$ is an algebraic extension over $\mathbb {Q}$ (if $a+b{\sqrt {2}}$ is any element of $\mathbb {Q} ({\sqrt {2}})$then it is a root of $f(x)=(x-a)^{2}-2b^{2}$) but $\mathbb {R}$ is not algebraic over $\mathbb {Q}$ because for example $\pi$ is not the root of any rational polynomial (this is a very difficult statement to prove).

Definition (Minimal Polynomial)

If $x$ is algebraic over $F$ then the set of polynomials in $F[x]$ which have $x$ as a root is an ideal of $F[x]$. This is a principle ideal domain and so the ideal is generated by a unique monic non-zero polynomial, $m(x)$. We define the $m(x)$ to be the minimal polynomial.

For example, the minimal polynomial of $i$ is $x^{2}+1$ and the minimal polynomial of ${\sqrt[{3}]{2}}$ is $x^{3}-2$, both over $\mathbb {Q}$. Note the minimal polynomial is heavily reliant on the field it is being viewed over. The minimal polynomial of ${\sqrt[{3}]{2}}$ over $\mathbb {R}$ is simply $x-{\sqrt[{3}]{2}}$.

Splitting Fields

Our primary goal in this study is to find the roots of a given polynomial. The brilliant insight of Galois and Galois theory is to (try to) answer this question by looking at field extensions. The following two lemmas might help motivate this reasoning.

Lemma 4.1.2

Suppose $F$ is a field $f(x)\in F[x]$ is a polynomial. Then there exists a (finite) field extension $E$ of $F$ such that $E$ contains a root of $f(x)$.

Proof. Suppose first that $f(x)$ is irreducible. Then we can take $E=F[x]/(f(x))$. We know that $E$ is indeed a field because $f(x)$ is irreducible. Moreover it contains an isomorphic copy of $F$ as the (equivalence classes of) the constant polynomials. Finally $[x]$, the equivalence class of the linear polynomial $x$, is a root of $f(x)$ since $$f([x])=[f(x)]=0\in F[x]/(f(x))$$Finally the degree of $E$ over $F$ is exactly the degree of the polynomial $f(x)$ (which hopefully motivates the terminology). This is due to the division algorithm. Suppose $g(x)$ is any polynomial in $F[x]$. Then we know by the division algorithm that there exist unique polynomials $q(x)$ and $r(x)$ such that $$g(x)=q(x)f(x)+r(x)$$where $\deg(r(x))<\deg(f(x))$. In particular, this means every equivalence class $[g(x)]$ contains a unique representative whose degree is less than $\deg(f(x))$. Therefore $E$ is spanned by $\{1,[x],[x^{2}],\dots ,[x^{n-1}]\}$ where $n=\deg(f(x))$. If $f(x)$ is not irreducible then it can be written as a product of irreducibles and applying the above process to any of these produces an extension which contains a root of at least one of these irreducible polynomials and hence contains a root of $f(x)$.    $\blacksquare$

We know $x^{2}+1$ is irreducible over $\mathbb {R}$, therefore $\mathbb {R} [x]/(x^{2}+1)$ is a field and one can verify that this field is isomorphic to $\mathbb {C}$. In fact, sometimes one defines the complex numbers as this quotient $\mathbb {R} [x]/(x^{2}+1)$.

Lemma 4.1.3

Suppose $E$ is an extension over $F$. Let $f(x)$ be an irreducible polynomial in $F[x]$ such that $E$ contains $\alpha$, a root of $f(x)$. Let $F(\alpha )$ be the smallest subfield of $E$ containing $F$ and $\alpha$. Then $F(\alpha )\cong F[x]/(f(x))$.

Proof. By the smallest subfield containing $F$ and $\alpha$, we mean the intersection of all subfields of $E$ that contain them. This collection of fields is non-empty since it contains $E$ for instance and it is easy to see that the intersection of subfields is again a subfield.

If $f(x)$ is of degree 1, then we are done since that would mean that $\alpha \in F$ so $F(\alpha )=F$ and by the argument towards the end of Lemma 4.1.1, we have $F[x]/(f(x))\cong F$. Then we can assume that $\deg(f(x))\geq 2$.

In order to show the isomorphism, we define a ring homomorphism $${\begin{aligned}\varphi :F[x]&\to F(\alpha )\\g(x)&\mapsto g(\alpha )\end{aligned}}$$In other words, $\varphi$ acts on polynomials by simply evaluating them at $\alpha$. By definition, we know that $f(x)\in {\textrm {ker}}(\varphi )$ since $f(\alpha )=0$. Since $f(x)$ is irreducible by assumption, it must also then generate the kernel (otherwise it would be a non-trivial multiple of the the generator of the kernel). Then by the First Isomorphism Theorem, we know that $F[x]/(f(x))$ is isomorphic to a subfield of $F(\alpha )$. Notice that $F[x]/(f(x))$ contains $F$ as the image of the constant polynomials and it contains $\alpha$ as the image of $x$. By assumption, $F(\alpha )$ was the smallest subfield containing these two things so we must have $F[x]/(f(x))\cong F(\alpha )$.     $\blacksquare$

The first lemma above tells us that we can always find a field extension containing the root of an irreducible polynomial by modding out by the polynomial. The second lemma tells us that any field extension containing a solution is of this form (up to isomorphism). Thus we will spend considerable time looking at the ring of polynomials over a field and studying its quotient spaces.

One often thinks of $F(\alpha )$ as 'adjoining' the root $\alpha$ to the field $F$. Roughly speaking, we add $\alpha$ to the field and then we close it under the field operations by also adding in all the possible sums, products, inverses, etc. and the further condition that $\alpha$ satisfies the given polynomial. In fact, this is precisely what the construction in the previous lemma does.

An important consequence of Lemma 4.1.3 is that the roots of an irreducible polynomial are algebraically indistinguishable (this is made precise in Theorem 4.1.4 and in particular by its Corollary 4.1.5). For example, we know that ${\sqrt {2}}$ and $-{\sqrt {2}}$ are both solutions of $x^{2}-2$. There is no algebraic distinction between the two roots; to differentiate them we need topological information like the fact that $-{\sqrt {2}}<0$ and ${\sqrt {2}}>0$. Similarly, $i$ and $-i$ are both solutions to $x^{2}+1$. Interchanging these roots is exactly what leads to complex conjugation. The fact that roots of (irreducible) polynomials are all equivalent to one another is one of the key ideas of Galois Theory.

Theorem 4.1.4

Let $F,{\widetilde {F}}$ be fields and $f(x)\in F[x]$ be an irreducible polynomial. Let $\varphi :F\to {\widetilde {F}}$ be an isomorphism of fields. Let ${\widetilde {f}}(x)$ be the polynomial $\varphi _{*}(f(x))$. Let $\alpha$ be a root of $f(x)$ (in some extension of $F$) and let $\beta$ be a root of ${\widetilde {f}}(x)$ (in some extension of ${\widetilde {F}}$). Then there exists an isomorphism $\sigma :F(\alpha )\to {\widetilde {F}}(\beta )$ that agrees with $\varphi$ on $F$.

Proof. Since $\varphi$ is an isomorphism and $f(x)$ is irreducible, we must have ${\widetilde {f}}(x)$ is also irreducible (since if we had ${\widetilde {f}}(x)=g_{1}(x)g_{2}(x)$ then $f(x)=(\varphi ^{-1})_{*}(g_{1}(x))\cdot (\varphi ^{-1})_{*}(g_{2}(x))$ which would contradict irreducibility of $f(x)$). Then $f(x)$ and ${\widetilde {f}}(x)$ generate maximal ideals in their respective rings and the ring isomorphism $\varphi _{*}$ descends to an isomorphism (of fields) of the quotients$$F[x]/(f(x))\to {\widetilde {F}}[x]/({\widetilde {f}}(x))$$We know by the previous theorem that the domain is isomorphic to $F(\alpha )$ and the codomain is isomorphic to ${\widetilde {F}}(\beta )$ and this map agrees with $\varphi$ on $F$ by construction.     $\blacksquare$

Corollary 4.1.5

Let $F,{\widetilde {F}}$ be fields and $f(x)\in F[x]$ be an irreducible polynomial. Suppose $\alpha ,\beta$ are roots of $f(x)$ in some (potentially different) extensions of $F$. Then $F(\alpha )\cong F(\beta )$.

Proof. Apply the previous theorem to case with $F={\widetilde {F}}$ and $\varphi$ as the identity map.

Definition (Splitting Field)

Let $F$ be a field, $f(x)\in F[x]$ and $a_{1},a_{2},...,a_{n}$ are roots of $f(x)$. Then the smallest field extension $E$ of $F$ which contains $a_{1},...,a_{n}$ is called a splitting field of $f(x)$ over $F$. In other words, no proper subfield of $E$ contains $F$ and all $a_{1},\dots ,a_{n}$.

Existence and Uniqueness of Splitting Fields

We will see that rather than looking at arbitrary field extension, splitting fields will be the things to consider. First we need to know that they always exist.

Theorem 4.1.6

Let $F$ be a field and $f(x)\in F[x]$ a polynomial. Then there exists a field extension $E$ of $F$ that is a splitting field of $f(x)$.

Proof. This is a largely uninteresting case of proof by induction. We will induct on the degree of $f(x)$. If $f(x)$ is linear, then clearly its roots (in fact just the one root) is contained in $F$ so $F$ itself is a splitting field. Suppose $\deg(f(x))>1$. If $f(x)$ splits into the product of linear terms, then again all the roots are contained in $F$, so we already have a splitting field. So suppose $f(x)$ has an irreducible factor of degree at least 2. Then there exists a field extension $E_{1}$ containing a root $\alpha$ of $f(x)$. Then in $E_{1}$, we can factorise the polynomial into $f(x)=(x-\alpha )f_{1}(x)$ where $f_{1}(x)$ is a polynomial of degree $\deg(f(x))-1$. Then by induction there exists $E_{2}$ a field extension of $E_{1}$ that is a splitting field of $f_{1}(x)$. Therefore $E_{2}$ is a field extension of $F$ that contains all the roots of $f(x)$. Taking the intersection of all subfields of $E_{2}$ containing $F$ and the roots of $f(x)$ gives us $E$, a splitting field of $f(x)$. $\blacksquare$

Above we were careful to say a splitting field of $f(x)$. In fact, this was an unnecessary precaution since the splitting field of a polynomial is unique up to isomorphism. This follows from a generalisation of Theorem 4.1.4, where we claim the statement of the theorem holds even if we adjoin all the roots of the polynomial, instead of just one.

Theorem 4.1.7

Let $F,{\widetilde {F}}$ be fields and $f(x)\in F[x]$ be a polynomial. Let $\varphi :F\to {\widetilde {F}}$ be an isomorphism of fields. Let ${\widetilde {f}}(x)$ be the polynomial $\varphi _{*}(f(x))$. Let $E$ a splitting field of $f(x)$ and ${\widetilde {E}}$ a splitting field of ${\widetilde {f}}(x)$. Then there exists an isomorphism $\sigma :E\to {\widetilde {E}}$ that agrees with $\varphi$ on $F$.

Proof. This is once again a proof by induction on the degree of $f(x)$. If $f(x)$ is of degree 1 or indeed splits into factors of degree 1 then the splitting field of $f(x)$ is $F$ so we can take $\sigma =\varphi$. Thus suppose $f(x)$ has an irreducible factor $p(x)$ of degree at least 2 so ${\widetilde {p}}(x)=\varphi _{*}(p(x))$is an irreducible factor of ${\widetilde {f}}(x)$. Then by the previous theorem we know $\varphi$ extends to an isomorphism $\psi :F(\alpha )\to {\widetilde {F}}(\beta )$ where $\alpha$ is a root of $p(x)$ and $\beta$ is a root of ${\widetilde {p}}(x)$. Therefore over $F(\alpha )$ and ${\widetilde {F}}(\beta )$ respectively we can write $f(x)=(x-\alpha )f_{1}(x)$ and ${\widetilde {f}}(x)=(x-\beta ){\widetilde {f}}_{1}(x)$. Notice that $E$ is a splitting field of $f_{1}(x)$ over $F(\alpha )$. Indeed if a splitting field was strictly contained within $E$, then it would contain all the roots of $f_{1}(x)$ and $\alpha$ and hence would contain all the roots of $f(x)$. But this would contradict $E$ being a splitting field of $f(x)$. Of course the same holds true for ${\widetilde {f}}_{1}(x)$ over ${\widetilde {F}}(\beta )$. Since $f_{1}(x)$ and ${\widetilde {f}}_{1}(x)$ have degree strictly less than $\deg(f(x))$, by induction we can assume that the statement of theorem holds for them. In particular, $\psi$ extends to an isomorphism $\sigma :E\to {\widetilde {E}}$. But since $\psi$ was an extension of $\varphi$, $\sigma$ must also be an extension of $\varphi$ concluding the proof.    $\blacksquare$

Corollary 4.1.8

Let $F$ be a field and $f(x)\in F[x]$ be a polynomial. If $E,{\widetilde {E}}$ are splitting fields of $f(x)$, then they are isomorphic.

Proof. Apply Theorem 4.1.7 to the case with $F={\widetilde {F}}$ and $\varphi$ as the identity map.     $\blacksquare$

Classification of Finite Fields

Theorem 4.1.9

If $F$ is a finite field, then $\mid F\mid =p^{n}$ for some prime $p$ and natural number $n$.

Proof. Since $F$ is a finite field and we know its prime subfield is $\mathbb {Z} _{p}$ for some prime $p$. The prime subfield is in particular a subfield of $F$ and hence $F$ forms a vector space over $\mathbb {Z} _{p}$. Since $F$ is finite, it must be a finite dimensional vector space and in particular we must have have $F\cong (\mathbb {Z} _{p})^{n}$ for some $n$ (as vector spaces) so $\mid F\mid =p^{n}$.     $\blacksquare$

Theorem (every member of F is a root of $x^{p^{n}}-x$)

let $F$ be a field such that $\left\vert F\right\vert =p^{n}$, then every member is a root of the polynomial $x^{p^{n}}-x$.

proof: Consider $F^{*}=F/{0}$ as a the multiplicative group. Then by la grange's theorem $\forall x\in F^{*},x^{p^{n}-1}=1$. So multiplying by $x$ gives $x^{p^{n}}=x$, which is true for all $x\in F$, including $0$.

Theorem (roots of $x^{p}-x$ are distinct)

Let $x^{p}-x$ be a polynomial in a splitting field $E$ over $\mathbb {Z} _{p}$ then the roots $a_{1},...a_{n}$ are distinct.

Factorization

One of the main motivations of this study is to determine the roots of a polynomial over a field. It is obvious that the roots of a product of polynomials is just their union (and in fact the multiplicities sum). Thus a good first step is to determine whether or not the given polynomial is a product of lower degree polynomials.

Recall we say a non-constant polynomial $f(x)\in F[x]$ is reducible if there exist non-constant polynomials $g(x)$ and $h(x)$ such that $f(x)=g(x)h(x)$. Otherwise, the polynomial is said to be irreducible. It is immediate that linear, i.e. degree 1, polynomials are irreducible. For low degree polynomials, it is easy to determine whether or not they are irreducible.

Lemma 4.2.1

If $f(x)\in F[x]$ is a degree 2 or degree 3 polynomial, it is reducible if and only if it has a root.

Proof. This simply amounts to noting that if $f(x)$ is of degree at most 3 then, any decomposition of the form $f(x)=g(x)h(x)$ must have at least one of $g(x)$ or $h(x)$ be linear. $\blacksquare$

Note that the statement does not hold for higher degree polynomials. For example $x^{4}-4$ has no roots in the rationals but $x^{4}-4=(x^{2}-2)(x^{2}+2)$ so it is reducible.

A case we are particularly interested in is polynomials over the rationals. A very useful theorem for this is the Rational Root Theorem which is a consequence of Gauss' Lemma.

Theorem 4.2.2 (Gauss' Lemma)

Let $f(x)\in \mathbb {Z} [x]$ be a primitive polynomial. Then $f(x)$ is irreducible over $\mathbb {Z} [x]$ if and only if it is irreducible over $\mathbb {Q} [x]$.

Proof. First we show that if $f(x)$ is reducible over $\mathbb {Q} [x]$ then it must be reducible over $\mathbb {Z} [x]$. Suppose we have $f(x)=g(x)h(x)$ where $g(x)$ and $h(x)$ are non-constant polynomials in $\mathbb {Q} [x]$. Suppose $d$ is the lowest common multiple of the denominators coefficients of the right hand side. Then$$df(x)=a(x)b(x)$$with $a(x),b(x)\in \mathbb {Z} [x]$. If $d=1$, we are done. So suppose $d>1$. We can write $d$ as a product of primes $d=p_{1}p_{2}\cdots p_{n}$. Modding out by $p_{1}$ we get$$0={\overline {a}}(x){\overline {b}}(x)$$where ${\overline {a}}(x),{\overline {b}}(x)$ are the corresponding polynomials in $\mathbb {Z} /p_{1}\mathbb {Z} [x]$ (in other words we mod each of the coefficients by $p_{1}$). Since $\mathbb {Z} /p_{1}\mathbb {Z} [x]$ is an integral domain, this means that at least one of the factors is 0. Without loss of generality we can assume that ${\overline {a}}(x)=0$. But this means that all of its coefficients are a multiple of $p_{1}$. Therefore we can cancel out $p_{1}$from both sides of the equation $df(x)=a(x)b(x)$. This leaves $n-1$ primes on the left hand side. We can apply the same argument and conclude via induction that $f(x)$ is reducible over $\mathbb {Z} [x]$.

The converse is easy to see since a decomposition over $\mathbb {Z} [x]$ is in particular a decomposition over $\mathbb {Q} [x]$. Since the coefficients don't share a factor this means that the decomposition is into a product of non-constant polynomials (in particular we avoid cases like $7x-7=7(x-1)$ which is a non-trivial decomposition in $\mathbb {Z} [x]$ but a trivial one in $\mathbb {Q} [x]$ since $7$ is only a unit in the latter ring).    $\blacksquare$

In particular this makes it easy to determine when a polynomial over the rationals has a rational root. Given $f(x)\in \mathbb {Q} [x]$, suppose it is monic with integer coefficients. Then if $f(x)$ has a root we can write $f(x)=(x-\alpha )(x^{n-1}+\cdots +\beta )$ where both factors have integer coefficients by Gauss' Lemma. Therefore in particular $\alpha$ is an integer and must be a factor of the constant polynomial. If $f(x)$ is not monic and its has a rational root $p/q$ then we would be able to write

$$f(x)=(px-q)(a_{n-1}x^{n-1}+\dots +a_{0})$$

In particular $p$ is a factor of the leading coefficient of $f(x)$ and $q$ is a factor of the constant term. This is known as the Rational Root Theorem. By trying all these possibilities, one can immediately determine whether or not there exist rational roots of a given polynomial over the rationals. (even if the coefficients are rational, one can multiply the polynomial by an integer to obtain a polynomial with integer coefficients and then work with this scaled polynomial, which has the same roots as the original).

Now that we know trying to reduce polynomials over $\mathbb {Q}$ is (essentially) equivalent to reducing them over $\mathbb {Z}$, it's useful to have some irreducibility criteria from the latter case. A very useful result for this is Eisenstein's criterion.

Lemma 4.2.3 (Eisenstein's Criterion)

Let $p$ be a prime in $\mathbb {Z}$ and $f(x)=x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}$ is a polynomial in $\mathbb {Z} [x]$. Suppose $p$ divides all the $a_{i}$ and $p^{2}$ does not divide the constant term $a_{0}$. Then $f(x)$ is irreducible over $\mathbb {Z} [x]$ and over $\mathbb {Q} [x]$.

Proof. Suppose $f(x)$ were reducible. Then there exist non-constant, monic polynomials $g(x),h(x)$ such that $f(x)=g(x)h(x)$. Consider the polynomial in the quotient $\mathbb {Z} /p\mathbb {Z}$. We find that$$x^{n}={\overline {g}}(x){\overline {h}}(x)$$

where ${\overline {g}}(x)$ and ${\overline {h}}(x)$ are the respective polynomials modulo $p$ (in other words ${\overline {g}}(x)=\pi _{*}(g(x))$ where $\pi :\mathbb {Z} \to \mathbb {Z} /p\mathbb {Z}$ is the canonical projection map). Since $g(x)$ and $h(x)$ were taken to be monic, we know their reductions ${\overline {g}}(x)$ and ${\overline {h}}(x)$ are also monic and hence non-constant. In particular then ${\overline {g}}(x){\overline {h}}(x)$ is a non-trivial decomposition of $x^{n}$.

By comparing coefficients above, we see that the product above has no constant term. Therefore at least one of ${\overline {g}}(x)$ and ${\overline {h}}(x)$ has no constant term (this is where we use the fact that $p$ is prime so in particular $\mathbb {Z} /p\mathbb {Z}$ is an integral domain). Suppose one of them does have a non-zero constant term. Then their product would contain lower degree terms but we know their product is exactly $x^{n}$. Therefore both ${\overline {g}}(x)$ and ${\overline {h}}(x)$ have no constant term. But this means the constant terms of $g(x)$ and $h(x)$ are both multiples of $p$ so in particular their product $a_{0}$ is a multiple of $p^{2}$ leading to a contradiction.     $\blacksquare$

Example: From Eisenstein's criterion, it is immediate that $x^{n}-2$ is irreducible over $\mathbb {Z}$ and hence over $\mathbb {Q}$ (by Gauss' Lemma). This is one way to show that ${\sqrt[{n}]{2}}$ are all irrational for $n\geq 1$.

Example: Here is a more sophisticated example. Consider the polynomial $$f(x)={\frac {x^{p}-1}{x-1}}=x^{p-1}+x^{p-2}+\cdots +x+1$$where $p$ is a prime. We observe that $$f(x+1)={\frac {(x+1)^{p}-1}{x}}={\frac {1}{x}}\sum _{k=1}^{p}{\binom {p}{k}}x^{k}=\sum _{k=0}^{p-1}{\binom {p}{k+1}}x^{k}$$In particular then $f(x+1)$ is a monic polynomial where every non-leading coefficient is a multiple of $p$ and the constant term is exactly $p$. Therefore by Eisenstein's criterion $f(x+1)$ is irreducible which in turn means that $f(x)$ is irreducible.

Once we have an irreducible polynomial, we know we can't decompose it any further so we need to start working with field extensions and splitting fields.

Exercises

1. Show that $x^{2}+x+1$ is irreducible over $\mathbb {F} _{2}$.
2. Find all irreducible polynomials of degree at most 3 over $\mathbb {F} _{2}$ and $\mathbb {F} _{3}$.
3. Show that $x^{2}+2$ is irreducible over $\mathbb {Q} (i)$.
4. Show that if ${\frac {x^{n}-1}{x-1}}$ is irreducible then $n$ is prime. Hint: Prove the contrapositive.

Splitting Fields and Algebraic Closures

Splitting Fields

Let F be a field and p(x) be a nonconstant polynomial in F(x). We already know that we can find a field extension of F that contains a root of p(x). However, we would like to know whether an extension E of F containing all of the roots of p(x) exists. In other words, can we find a field extension of F such that p(x) factors into a product of linear polynomials? What is the "smallest" extension containing all the roots of p(x)?

Let F be a field and $p(x)=\alpha _{0}+\alpha _{1}x+\cdots +\alpha _{n}x^{n}$ be a nonconstant polynomial in F[x]. An extension field E of F is a splitting field of p(x) if there exist elements $\alpha _{1},\cdots ,\alpha _{n}$ in E such that $E=F(\alpha _{1},\cdots ,\alpha _{n})$ and

$p(x)=(x-\alpha _{1})(x-\alpha _{2})\cdots (x-\alpha _{n})$ in E[x].

A polynomial $p(x)\in F[x]$ splits in E if it is the product of linear factors in E[x].

Example 1: Let $p(x)=x^{4}+2x^{2}-8$ be in $\mathbb {Q} [x]$. Then p(x) has irreducible factors $x^{2}-2$ and $x^{2}+4$. Therefore, the field $\mathbb {Q} ({\sqrt {2}},i)$ is a splitting field for p(x).

Example 2: Let $p(x)=x^{3}-3$ be in $\mathbb {Q} [x]$. Then p(x) has a root in the field $\mathbb {Q} ({\sqrt[{3}]{3}})$. However, this field is not a splitting field for p(x) since the complex cube roots of 3, ${\frac {-{\sqrt[{3}]{3}}\pm ({\sqrt[{6}]{3}})^{5}i}{2}}$ are not in $\mathbb {Q} ({\sqrt[{3}]{3}})$.

Theorem Let p(x) $\in$ F(x) be a nonconstant polynomial. Then there exists a splitting field E for p(x).

Proof. We will use mathematical induction on the degree of p(x). If $deg(p(x))=1$, then p(x) is a linear polynomial and $E=F$. Assume that the theorem is true for all polynomials of degree k with $1\leq k<n$ and let $deg(p(x))=n$. We can assume that p(x) is irreducible; otherwise, by our induction hypothesis, we are done. There exists a field K such that p(x) has a zero $\alpha _{1}$ in K. Hence, $p(x)=(x-\alpha _{1})q(x)$, where $q(x)\in K(x)$. Since $deg(q(x))=n-1$, there exists a splitting field $E\supset K$ of q(x) that contains the zeros $\alpha _{2},\cdots ,\alpha _{n}$ of p(x) by our induction hypothesis. Consequently,

$E=K(\alpha _{2},\cdots ,\alpha _{n})=F(\alpha _{1},\cdots ,\alpha _{n})$

is a splitting field of p(x).

The question of uniqueness now arises for splitting fields. This question is answered in the affirmative. Given two splitting fields K and L of a polynomial $p(x)\in F(x)$, there exists a field isomorphism $\phi :K\to L$ that preserves F. In order to prove this result, we must first prove a lemma.

Lemma Theorem Let $\phi :E\to F$ be an isomorphism of fields. Let K be an extension field of E and $\alpha \in K$ be algebraic over E with minimal polynomial p(x). Suppose that L is an extension field of F such that $\beta$ is root of the polynomial in F[x] obtained from p(x) under the image of $\phi$. Then $\phi$ extends to a unique isomorphism $\psi :E(\alpha )\to F(\beta )$ such that $\psi (\alpha )=\beta$ and $\psi$ agrees with $\phi$ on E.

Lemma Proof. If p(x) has degree n, then we can write any element in $E(\alpha )$ as a linear combination of $1,\alpha ,\cdots ,\alpha ^{n-1}$. Therefore, the isomorphism that we are seeking must be

$\phi (a_{0}+a_{1}\alpha +\cdots +a_{n-1}\alpha ^{n-1})=\psi (a_{0})+\psi (a_{1})\beta +\cdots +\psi (a_{n-1})\beta ^{n-1}$,

where

$a_{0}+a_{1}\alpha +\cdots +a_{n-1}\alpha ^{n-1}$

is an element in $E(\alpha )$. The fact that $\phi$ is an isomorphism could be checked by direct computation; however, it is easier to observe that $\phi$ is a composition of maps that we already know to be isomorphisms.

We can extend $\psi$ to be an isomorphism from E[x] to F[x], which we will also denote by $\psi$, by letting

$\psi (a_{0}+a_{1}x+\cdots +a_{n}x^{n})=\psi (a_{1})x+\cdots +\psi (a_{n})x^{n}$.

This extension agrees with the original isomorphism $\psi :E\to F$, since constant polynomials get mapped to constant polynomials. By assumption, $\psi (p(x))=q(x)$; hence, $\psi$ maps $\left\langle p(x)\right\rangle$ onto $\left\langle q(x)\right\rangle$. Consequently, we have an isomorphism ${\overline {\psi }}:E[x]/\left\langle p(x)\right\rangle \to F[x]/\left\langle q(x)\right\rangle$. We have isomorphisms $\sigma :E[x]/\left\langle p(x)\right\rangle \to F(\alpha )$ and $\tau :F[x]/\left\langle q(x)\right\rangle \to F(\beta )$, defined by evaluation at $\alpha$ and $\beta$, respectively. Therefore, $\psi =\tau ^{-1}{\overline {\phi }}\sigma$ is the required isomorphism.

Now write $p(x)=(x-\alpha )f(x)$ and $q(x)=(x-\beta )g(x)$, where the degrees of f(x) and g(x) are less than the degrees of p(x) and q(x), respectively. The field extension K is a splitting field for f(x) over E(α), and L is a splitting field for g(x) over F(β). By our induction hypotheses there exists an isomorphism $\psi :K\to L$ such that $\psi$ agrees with ${\bar {\phi }}$ on E(α). Hence, there exists an isomorphism $\psi :K\to L$ such that $\psi$ agrees with $\psi$ on E.

Corollary Let p(x) be a polynomial in F[x]. Then there exists a splitting field K of p(x) that is unique up to isomorphism.

Algebraic Closures

Given a field F, the question arises as to whether or not we can find a field E such that every polynomial p(x) has a root in E. This leads us to the following theorem.

Theorem 21.11 Let E be an extension field of F. The set of elements in E that are algebraic over F form a field.

Proof. Let $\alpha ,\beta \in E$ be algebraic over F. Then $F(\alpha ,\beta )$ is a finite extension of F. Since every element of $F(\alpha ,\beta )$ is algebraic over $F,\alpha \pm \beta ,\alpha \beta$, and $\alpha /\beta {\text{ }}(\beta \neq 0)$ are all algebraic over F. Consequently, the set of elements in E that are algebraic over F forms a field.

Corollary 21.12 The set of all algebraic numbers forms a field; that is, the set of all complex numbers that are algebraic over $\mathbb {Q}$ makes up a field.

Let E be a field extension of a field F. We define the algebraic closure of a field F in E to be the field consisting of all elements in E that are algebraic over F. A field F is algebraically closed if every nonconstant polynomial in F[x] has a root in F.

Theorem 21.13 A field F is algebraically closed if and only if every nonconstant polynomial in F[x] factors into linear factors over F[x].

Proof. Let F be an algebraically closed field. If $p(x)\in F[x]$ is a nonconstant polynomial, then p(x) has a zero in F, say α. Therefore, $x-\alpha$ must be a factor of p(x) and so $p(x)=(x-\alpha )q_{1}(x)$, where $deg(q_{1}(x))=deg(p(x))-1$. Continue this process with $q_{1}(x)$ to find a factorization

$p(x)=(x-\alpha )(x-\beta )q_{2}(x)$,

where $deg(q_{2}(x))=deg(p(x))-2$. The process must eventually stop since the degree of p(x) is finite.

Conversely, suppose that every nonconstant polynomial p(x) in F[x] factors into linear factors. Let $ax-b$ be such a factor. Then $p(b/a)=0$. Consequently, F is algebraically closed.

Corollary 21.14 An algebraically closed field F has no proper algebraic extension E.

Proof. Let E be an algebraic extension of F; then $F\subset E$. For $\alpha \in E$, the minimal polynomial of α is $x-\alpha$. Therefore, $\alpha \in F$ and $F=E$.

Theorem 21.15 Every field F has a unique algebraic closure.

It is a nontrivial fact that every field has a unique algebraic closure. The proof is not extremely difficult, but requires some rather sophisticated set theory. We refer the reader to [3], [4], or [8] for a proof of this result.

We now state the Fundamental Theorem of Algebra, first proven by Gauss at the age of 22 in his doctoral thesis. This theorem states that every polynomial with coefficients in the complex numbers has a root in the complex numbers. The proof of this theorem will be given in Abstract Algebra/Galois Theory.

Theorem 21.16 (Fundamental Theorem of Algebra) The field of complex numbers is algebraically closed.

Vector Spaces

Definition (Vector Space)

Let F be a field. A set V with two binary operations: + (addition) and $\times$ (scalar multiplication), is called a Vector Space if it has the following properties:

1. $(V,+)$ forms an abelian group
2. $(a+b)v=av+bv$ for $a,b\in F$ and $v\in V$
3. $a(v+u)=av+au$ for $a\in F$ and $v,u\in V$
4. $(ab)v=a(bv)$
5. $1_{F}v=v$

The scalar multiplication is formally defined by $F\times V{\xrightarrow {\phi }}V$, where $\phi ((f,v))=fv\in V$.

Elements in F are called scalars, while elements in V are called vectors.

Some Properties of Vector Spaces

1. $0_{F}v=0_{V}=a0_{V}$
2. $(-1_{F})v=-v$
3. $av=0\iff a=0{\text{ or }}v=0$

Proofs:

1. $0_{F}v=(0_{F}+0_{F})v=0_{F}v+0_{F}v\Rightarrow 0_{V}=0_{F}v.Also,a0_{V}=a(0_{V}+0_{V})=a0_{V}+a0_{V}\Rightarrow a0_{V}=0_{V}$
2. We want to show that $v+(-1_{F})v=0_{V}$, but $v+(-1_{F})v=1_{F}v+(-1_{F})v=(1_{F}+(-1_{F}))v=0_{F}v=0_{V}$
3. Suppose $av=0$ such that $a\neq 0$, then $a^{-1}(av)=a^{-1}0=0\Rightarrow 1_{F}v=v=0$

Algebras

In this section we will talk about structures with three operations. These are called algebras. We will start by defining an algebra over a field, which is a vector space with a bilinear vector product. After giving some examples, we will then move to a discussion of quivers and their path algebras.

Algebras over a Field

Definition 1: Let $F$ be a field, and let $A$ be an $F$-vector space on which we define the vector product $\cdot \,:\,A\times A\rightarrow A$. Then $A$ is called an algebra over $F$ provided that $(A,+,\cdot )$ is a ring, where $+$ is the vector space addition, and if for all $a,b,c\in A$ and $\alpha \in F$,

1. $a(bc)=(ab)c$,
2. $a(b+c)=ab+ac$ and $(a+b)c=ac+bc$,
3. $\alpha (ab)=(\alpha a)b=a(\alpha b)$.

The dimension of an algebra is the dimension of $A$ as a vector space.

Remark 2: The appropriate definition of a subalgebra is clear from Definition 1. We leave its formal statement to the reader.

Definition 2: If $(A,+,\cdot )$ is a commutative ring, $A$ is called a commutative algebra. If it is a division ring, $A$ is called a division algebra. We reserve the terms real and complex algebra for algebras over $\mathbb {R}$ and $\mathbb {C}$, respectively.

The reader is invited to check that the following examples really are examples of algebras.

Example 3: Let $F$ be a field. The vector space $F^{n}$ forms a commutative $F$-algebra under componentwise multiplication.

Example 4: The quaternions $\mathbb {H}$ is a 4-dimensional real algebra. We leave it to the reader to show that it is not a 2-dimensional complex algebra.

Example 5: Given a field $F$, the vector space of polynomials $F[x]$ is a commutative $F$-algebra in a natural way.

Example 6: Let $F$ be a field. Then any matrix ring over $F$, for example $\left({\begin{array}{cc}F&0\\F&F\end{array}}\right)$, gives rise to an $F$-algebra in a natural way.

Quivers and Path Algebras

Naively, a quiver can be understood as a directed graph where we allow loops and parallell edges. Formally, we have the following.

Definition 7: A quiver is a collection of four pieces of data, $Q=(Q_{0},Q_{1},s,t)$,

1. $Q_{0}$ is the set of vertices of the quiver,
2. $Q_{1}$ is the set of edges, and
3. $s,t\,:\,Q_{1}\rightarrow Q_{0}$ are functions associating with each edge a source vertex and a target vertex, respectively.

We will always assume that $Q_{0}$ is nonempty and that $Q_{0}$ and $Q_{1}$ are finite sets.

Example 8: The following are the simplest examples of quivers:

1. The quiver with one point and no edges, represented by $1$.
2. The quiver with $n$ point and no edges, $1\quad 2\quad ...\quad n$.
3. The linear quiver with $n$ points, $1\,{\stackrel {a_{1}}{\longrightarrow }}\,2\,{\stackrel {a_{2}}{\longrightarrow }}\,...\,{\xrightarrow {a_{n-1}}}\,n$.
4. The simplest quiver with a nontrivial loop, $1{\underset {a}{\stackrel {b}{\leftrightarrows }}}2$.

Definition 9: Let $Q$ be a quiver. A path in $Q$ is a sequence of edges $a=a_{m}a_{m-1}...a_{1}$ where $s(a_{i})=t(a_{i-1})$ for all $i=2,...,m$. We extend the domains of $s$ and $t$ and define $s(a)\equiv s(a_{0})$ and $t(a)\equiv t(a_{m})$. We define the length of the path to be the number of edges it contains and write $l(a)=m$. With each vertex $i$ of a quiver we associate the trivial path $e_{i}$ with $s(e_{i})=t(e_{i})=i$ and $l(e_{i})=0$. A nontrivial path $a$ with $s(a)=t(a)=i$ is called an oriented loop at $i$.

The reason quivers are interesting for us is that they provide a concrete way of constructing a certain family of algebras, called path algebras.

Definition 10: Let $Q$ be a quiver and $F$ a field. Let $FQ$ denote the free vector space generated by all the paths of $Q$. On this vector space, we define a vector product in the obvious way: if $u=u_{m}...u_{1}$ and $v=v_{n}...v_{1}$ are paths with $s(v)=t(u)$, define their product $vu$ by concatenation: $vu=v_{n}...v_{1}u_{m}...u_{1}$. If $s(v)\neq t(u)$, define their product to be $vu=0$. This product turns $FQ$ into an $F$-algebra, called the path algebra of $Q$.

Lemma 11: Let $Q$ be a quiver and $F$ field. If $Q$ contains a path of length $|Q_{0}|$, then $FQ$ is infinite dimensional.

Proof: By a counting argument such a path must contain an oriented loop, $a$, say. Evidently $\{a^{n}\}_{n\in \mathbb {N} }$ is a linearly independent set, such that $FQ$ is infinite dimensional.

Lemma 12: Let $Q$ be a quiver and $F$ a field. Then $FQ$ is infinite dimensional if and only if $Q$ contains an oriented loop.

Proof: Let $a$ be an oriented loop in $Q$. Then $FQ$ is infinite dimensional by the above argument. Conversely, assume $Q$ has no loops. Then the vertices of the quiver can be ordered such that edges always go from a lower to a higher vertex, and since the length of any given path is bounded above by $|Q_{0}|-1$, there dimension of $FQ$ is bounded above by $\mathrm {dim} \,FQ\leq |Q_{0}|^{2}-|Q_{0}|<\infty$.

Lemma 13: Let $Q$ be a quiver and $F$ a field. Then the trivial edges $e_{i}$ form an orthogonal idempotent set.

Proof: This is immediate from the definitions: $e_{i}e_{j}=0$ if $i\neq j$ and $e_{i}^{2}=e_{i}$.

Corollary 14: The element $\sum _{i\in Q_{0}}e_{i}$ is the identity element in $FQ$.

Proof: It sufficed to show this on the generators of $FQ$. Let $a$ be a path in $Q$ with $s(a)=j$ and $t(a)=k$. Then $\left(\sum _{i\in Q_{0}}e_{i}\right)a=\sum _{i\in Q_{0}}e_{i}a=e_{j}a=a$. Similarily, $a\left(\sum _{i\in Q_{0}}e_{i}\right)=a$.

To be covered:

- General R-algebras

Boolean algebra

Boolean Algebra

Boolean algebra is a deductive mathematical system closed over the values zero and one (false and true). A binary operator defined over this set of values accepts two boolean inputs and produces a single boolean output.

For any given algebra system, there are some initial assumptions, or postulates that the system follows. You can deduce additional rules, theorems, and other properties of the system from this basic set of postulates:

• Closure: The boolean system is closed with respect to a binary operator if for every pair of boolean values it produces a boolean result. For example, logical AND is closed in the boolean system because it accepts only boolean operands and produces only boolean results.
• Commutativity: A binary operator "#" is said to be commutative if A # B = B # A for all possible boolean values A and B.
• Associativity: A binary operator "#" is said to be associative if (A # B) # C = A # (B # C) for all boolean values A, B, and C.
• Distribution: Two binary operators "#" and "%" are distributive if A # (B % C) = (A # B) % (A # C) for all boolean values A, B, and C.
• Identity: A boolean value I is said to be the identity element with respect to some binary operator "#" if A # I = A
• Inverse: A boolean value I is said to be the inverse element with respect to some binary operator "#" if A # I = B and B ≠ A (i.e., B is the opposite value of A).

For our purposes, we will base boolean algebra on the following set of operators and values:

• The two possible values in the boolean system are zero and one. Often we will call these values false and true (respectively).
• The symbol "∧" represents the logical AND operation (conjunction); e.g., A ∧ B is the result of logically ANDing the boolean values A and B. When using single letter variable names, this text will drop the "∧" symbol; Therefore, AB also represents the logical AND of the variables A and B (we will also call this the product of A and B).
• The symbol "∨" represents the logical OR operation (disjunction); e.g., A ∨ B is the result of logical ORing the boolean values A and B. (We will also call this the sum of A and B.)
• Logical complement, negation, or NOT, is a unary operator. This text will use the prime symbol (′) to denote logical negation. For example, A′ denotes the logical NOT of A.
• If several different operators appear in a single boolean expression, the result of the expression depends on the precedence of the operators. We'll use the following precedences (from highest to lowest) for the boolean operators: parenthesis, logical NOT, logical AND, then logical OR. The logical AND and OR operators are left associative. The logical NOT operation is right associative, although it would produce the same result using left or right associativity since it is a unary operator.

We will also use the following set of postulates:

1. Boolean algebra is closed under the AND, OR, and NOT operations.
2. The identity element with respect to ∧ is one and ∨ is zero. There is no identity element with respect to logical NOT.
3. The ∧ and ∨ operators are commutative.
4. ∧ and ∨ are distributive with respect to one another. That is, A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) and A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C).
5. For every value A there exists a value A′ such that A ∧ A′ = 0 and A ∨ A′ = 1. This value is the logical complement (or NOT) of A.
6. ∧ and ∨ are both associative. That is, (A ∧ B) ∧ C = A ∧ (B ∧ C) and (A ∨ B) ∨ C = A ∨ (B ∨ C).

You can prove all other theorems in boolean algebra using these postulates. This text will not go into the formal proofs of these theorems, however, it is a good idea to familiarize yourself with some important theorems in boolean algebra. A sampling include:

1. A ∨ A = A
2. A ∧ A = A
3. A ∨ 0 = A
4. A ∧ 1 = A
5. A ∧ 0 = 0
6. A ∨ 1 = 1
7. (A ∨ B)′ = A′ ∧ B′
8. (A ∧ B)′ = A′ ∨ B′
9. A ∨ A ∧ B = A
10. A ∧ (A ∨ B) = A
11. A ∨ A′B = A ∨ B
12. A′ ∧ (A ∨ B′) = A′ B′
13. AB ∨ AB′ = A
14. (A′ ∨ B′) ∧ (A′ ∨ B) = A′
15. A ∨ A′ = 1
16. A ∧ A′ = 0

Theorems seven and eight above are known as DeMorgan's Theorems after the mathematician who discovered them.

The theorems above appear in pairs. Each pair (e.g. 1 & 2, 3 & 4, etc.) form a dual. An important principle in the boolean algebra system is that of duality. Any valid expression you can create using the postulates and theorems of boolean algebra remains valid if you interchange the operators and constants appearing in the expression. Specifically, if you exchange the ∧ and ∨ operators and swap the 0 and 1 values in an expression. you will wind up with an expression that obeys all the rules of boolean algebra. This does not mean the dual expression computes the same values, it only means that both expressions are legal in the boolean algebra system. Therefore, this is an easy way to generate a second theorem for any fact you prove in the boolean algebra system.

Although we will not be proving any theorems for the sake of boolean algebra in this text, we will use these theorems to show that two boolean equations are identical. This is an important operation when attempting to produce canonical representations of a boolean expression or when simplifying a boolean expression.

Boolean Functions and Truth Tables

A boolean expression is a sequence of zeros, ones, and literals separated by boolean operators. A literal is a primed (negated) or unprimed variable name. For our purposes, all variable names will be a single alphabetic character. A boolean function is a specific boolean expression; we will generally give boolean functions the name "F" with a possible subscript. For example, consider the following function:

F₀ = AB ∨ C

This function computes the logical AND of A and B and then logically ORs this result with C. If A=1, B=0, and C=1, then F₀ returns the value one (1 ∧ 0 ∨ 1 = 1).

Another way to represent a boolean function is a via a truth table. The previous chapter used truth tables to represent the AND and OR functions. Those truth tables took the forms:

AND Truth Table

AND	0	1
0	0	0
1	0	1

OR Truth Table

OR	0	1
0	0	1
1	1	1

For binary operators with two input variables, this form of a truth table is very natural and convenient. However, reconsider the boolean function F₀ above. That function has three input variables, not two. Therefore, one cannot use the truth table format given above. Fortunately, it is still very easy to construct truth tables for three or more variables. The following example shows one way to do this for functions of three variables:

A	B	C	AB	AB ∨ C
0	0	0	0	0
0	0	1	0	1
0	1	0	0	0
0	1	1	0	1
1	0	0	0	0
1	0	1	0	1
1	1	0	1	1
1	1	1	1	1

Clifford Algebras

In mathematics, Clifford algebras are a type of associative algebra. They can be thought of as one of the possible generalizations of the complex numbers and quaternions. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry and theoretical physics. They are named for the English geometer William Clifford.

Some familiarity with the basics of multilinear algebra will be useful in reading this section.

Introduction and basic properties

Specifically, a Clifford algebra is a unital associative algebra which contains and is generated by a vector space V equipped with a quadratic form Q. The Clifford algebra Cℓ(V,Q) is the "freest" algebra generated by V subject to the condition¹

$v^{2}=Q(v)\ {\mbox{ for all }}v\in V.$

If the characteristic of the ground field K is not 2, then one can rewrite this fundamental identity in the form

$uv+vu=\langle u,v\rangle {\mbox{ for all }}u,v\in V,$

where <u, v> = Q(u + v) − Q(u) − Q(v) is the symmetric bilinear form associated to Q. This idea of "freest" or "most general" algebra subject to this identity can be formally expressed through the notion of a universal property (see below).

Clifford algebras are closely related to exterior algebras. In fact, if Q = 0 then the Clifford algebra Cℓ(V,Q) is just the exterior algebra Λ(V). For nonzero Q there exists a canonical linear isomorphism between Λ(V) and Cℓ(V,Q) whenever the ground field K does not have characteristic two. That is, they are naturally isomorphic as vector spaces, but with different multiplications (in the case of characteristic two, they are still isomorphic as vector spaces, just not naturally). Clifford multiplication is strictly richer than the exterior product since it makes use of the extra information provided by Q. More precisely, they may be thought of as quantizations of the exterior algebra, in the same way that the Weyl algebra is a quantization of the symmetric algebra.

Quadratic forms and Clifford algebras in characteristic 2 form an exceptional case. In particular, if char K = 2 it is not true that a quadratic form is determined by its symmetric bilinear form, or that every quadratic form admits an orthogonal basis. Many of the statements in this article include the condition that the characteristic is not 2, and are false if this condition is removed.

Universal property and construction

Let V be a vector space over a field K, and let Q : V → K be a quadratic form on V. In most cases of interest the field K is either R or C (which have characteristic 0) or a finite field.

A Clifford algebra Cℓ(V,Q) is a unital associative algebra over K together with a linear map i : V → Cℓ(V,Q) defined by the following universal property: Given any associative algebra A over K and any linear map j : V → A such that

j(v)² = Q(v)1 for all v ∈ V

(where 1 denotes the multiplicative identity of A), there is a unique algebra homomorphism f : Cℓ(V,Q) → A such that the following diagram commutes (i.e. such that f o i = j):

Working with a symmetric bilinear form <·,·> instead of Q (in characteristic not 2), the requirement on j is

j(v)j(w) + j(w)j(v) = <v, w> for all v, w ∈ V.

A Clifford algebra as described above always exists and can be constructed as follows: start with the most general algebra that contains V, namely the tensor algebra T(V), and then enforce the fundamental identity by taking a suitable quotient. In our case we want to take the two-sided ideal I_Q in T(V) generated by all elements of the form

$v\otimes v-Q(v)1$ for all $v\in V$

and define Cℓ(V,Q) as the quotient

Cℓ(V,Q) = T(V)/I_Q.

It is then straightforward to show that Cℓ(V,Q) contains V and satisfies the above universal property, so that Cℓ is unique up to isomorphism; thus one speaks of "the" Clifford algebra Cℓ(V, Q). It also follows from this construction that i is injective. One usually drops the i and considers V as a linear subspace of Cℓ(V,Q).

The universal characterization of the Clifford algebra shows that the construction of Cℓ(V,Q) is functorial in nature. Namely, Cℓ can be considered as a functor from the category of vector spaces with quadratic forms (whose morphisms are linear maps preserving the quadratic form) to the category of associative algebras. The universal property guarantees that linear maps between vector spaces (preserving the quadratic form) extend uniquely to algebra homomorphisms between the associated Clifford algebras.

Basis and dimension

If the dimension of V is n and {e₁,…,e_n} is a basis of V, then the set

$\{e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}\mid 1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n{\mbox{ and }}0\leq k\leq n\}$

is a basis for Cℓ(V,Q). The empty product (k = 0) is defined as the multiplicative identity element. For each value of k there are n choose k basis elements, so the total dimension of the Clifford algebra is

$\dim C\ell (V,Q)=\sum _{k=0}^{n}{\begin{pmatrix}n\\k\end{pmatrix}}=2^{n}.$

Since V comes equipped with a quadratic form, there is a set of privileged bases for V: the orthogonal ones. An orthogonal basis in one such that

$\langle e_{i},e_{j}\rangle =0\qquad i\neq j.\,$

where <·,·> is the symmetric bilinear form associated to Q. The fundamental Clifford identity implies that for an orthogonal basis

$e_{i}e_{j}=-e_{j}e_{i}\qquad i\neq j.\,$

This makes manipulation of orthogonal basis vectors quite simple. Given a product $e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}$ of distinct orthogonal basis vectors, one can put them into standard order by including an overall sign corresponding to the number of flips needed to correctly order them (i.e. the signature of the ordering permutation).

If the characteristic is not 2 then an orthogonal basis for V exists, and one can easily extend the quadratic form on V to a quadratic form on all of Cℓ(V,Q) by requiring that distinct elements $e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}$ are orthogonal to one another whenever the {e_i}'s are orthogonal. Additionally, one sets

$Q(e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}})=Q(e_{i_{1}})Q(e_{i_{2}})\cdots Q(e_{i_{k}})$.

The quadratic form on a scalar is just Q(λ) = λ². Thus, orthogonal bases for V extend to orthogonal bases for Cℓ(V,Q). The quadratic form defined in this way is actually independent of the orthogonal basis chosen (a basis-independent formulation will be given later).

Examples: Real and complex Clifford algebras

The most important Clifford algebras are those over real and complex vector spaces equipped with nondegenerate quadratic forms.

Every nondegenerate quadratic form on a finite-dimensional real vector space is equivalent to the standard diagonal form:

$Q(v)=v_{1}^{2}+\cdots +v_{p}^{2}-v_{p+1}^{2}-\cdots -v_{p+q}^{2}$

where n = p + q is the dimension of the vector space. The pair of integers (p, q) is called the signature of the quadratic form. The real vector space with this quadratic form is often denoted R^p,q. The Clifford algebra on R^p,q is denoted Cℓ_p,q(R). The symbol Cℓ_n(R) means either Cℓ_n,0(R) or Cℓ_0,n(R) depending on whether the author prefers positive definite or negative definite spaces.

A standard orthonormal basis {e_i} for R^p,q consists of n = p + q mutually orthogonal vectors, p of which have norm +1 and q of which have norm −1. The algebra Cℓ_p,q(R) will therefore have p vectors which square to +1 and q vectors which square to −1.

Note that Cℓ_0,0(R) is naturally isomorphic to R since there are no nonzero vectors. Cℓ_0,1(R) is a two-dimensional algebra generated by a single vector e₁ which squares to −1, and therefore is isomorphic to C, the field of complex numbers. The algebra Cℓ_0,2(R) is a four-dimensional algebra spanned by {1, e₁, e₂, e₁e₂}. The latter three elements square to −1 and all anticommute, and so the algebra is isomorphic to the quaternions H. The next algebra in the sequence is Cℓ_0,3(R) is an 8-dimensional algebra isomorphic to the direct sum H ⊕ H called Clifford biquaternions.

One can also study Clifford algebras on complex vector spaces. Every nondegenerate quadratic form on a complex vector space is equivalent to the standard diagonal form

$Q(z)=z_{1}^{2}+z_{2}^{2}+\cdots +z_{n}^{2}$

where n = dim V, so there is essentially only one Clifford algebra in each dimension. We will denote the Clifford algebra on Cⁿ with the standard quadratic form by Cℓ_n(C). One can show that the algebra Cℓ_n(C) may be obtained as the complexification of the algebra Cℓ_p,q(R) where n = p + q:

$C\ell _{n}(\mathbb {C} )\cong C\ell _{p,q}(\mathbb {R} )\otimes \mathbb {C} \cong C\ell (\mathbb {C} ^{p+q},Q\otimes \mathbb {C} )$.

Here Q is the real quadratic form of signature (p,q). Note that the complexification does not depend on the signature. The first few cases are not hard to compute. One finds that

Cℓ₀(C) = C

Cℓ₁(C) = C ⊕ C

Cℓ₂(C) = M₂(C)

where M₂(C) denotes the algebra of 2×2 matrices over C.

It turns out that every one of the algebras Cℓ_p,q(R) and Cℓ_n(C) is isomorphic to a matrix algebra over R, C, or H or to a direct sum of two such algebras. For a complete classification of these algebras see classification of Clifford algebras.

Properties

Relation to the exterior algebra

Given a vector space V one can construct the exterior algebra Λ(V), whose definition is independent of any quadratic form on V. It turns out that if F does not have characteristic 2 then there is a natural isomorphism between Λ(V) and Cℓ(V,Q) considered as vector spaces (and there exists an isomorphism in characteristic two, which may not be natural). This is an algebra isomorphism if and only if Q = 0. One can thus consider the Clifford algebra Cℓ(V,Q) as an enrichment (or more precisely, a quantization, cf. the Introduction) of the exterior algebra on V with a multiplication that depends on Q (one can still define the exterior product independent of Q).

The easiest way to establish the isomorphism is to choose an orthogonal basis {e_i} for V and extend it to an orthogonal basis for Cℓ(V,Q) as described above. The map Cℓ(V,Q) → Λ(V) is determined by

$e_{i_{1}}e_{i_{2}}\cdots e_{i_{k}}\mapsto e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}}.$

Note that this only works if the basis {e_i} is orthogonal. One can show that this map is independent of the choice of orthogonal basis and so gives a natural isomorphism.

If the characteristic of K is 0, one can also establish the isomorphism by antisymmetrizing. Define functions f_k : V × … × V → Cℓ(V,Q) by

$f_{k}(v_{1},\cdots ,v_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}{\rm {sgn}}(\sigma )\,v_{\sigma (1)}\cdots v_{\sigma (k)}$

where the sum is taken over the symmetric group on k elements. Since f_k is alternating it induces a unique linear map Λ^k(V) → Cℓ(V,Q). The direct sum of these maps gives a linear map between Λ(V) and Cℓ(V,Q). This map can be shown to be a linear isomorphism, and it is natural.

A more sophisticated way to view the relationship is to construct a filtration on Cℓ(V,Q). Recall that the tensor algebra T(V) has a natural filtration: F⁰ ⊂ F¹ ⊂ F² ⊂ … where F^k contains sums of tensors with rank ≤ k. Projecting this down to the Clifford algebra gives a filtration on Cℓ(V,Q). The associated graded algebra

$\bigoplus _{k}F^{k}/F^{k-1}$

is naturally isomorphic to the exterior algebra Λ(V). Since the associated graded algebra of a filtered algebra is always isomorphic to the filtered algebra as filtered vector spaces (by choosing complements of F^k in F^k+1 for all k), this provides an isomorphism (although not a natural one) in any characteristic, even two.

Grading

The linear map on V defined by $v\mapsto -v$ preserves the quadratic form Q and so by the universal property of Clifford algebras extends to an algebra automorphism

α : Cℓ(V,Q) → Cℓ(V,Q).

Since α is an involution (i.e. it squares to the identity) one can decompose Cℓ(V,Q) into positive and negative eigenspaces

$C\ell (V,Q)=C\ell ^{0}(V,Q)\oplus C\ell ^{1}(V,Q)$

where Cℓⁱ(V,Q) = {x ∈ Cℓ(V,Q) | α(x) = (−1)ⁱx}. Since α is an automorphism it follows that

$C\ell ^{\,i}(V,Q)C\ell ^{\,j}(V,Q)=C\ell ^{\,i+j}(V,Q)$

where the superscripts are read modulo 2. This means that Cℓ(V,Q) is a Z₂-graded algebra (also known as a superalgebra). Note that Cℓ⁰(V,Q) forms a subalgebra of Cℓ(V,Q), called the even subalgebra. The piece Cℓ¹(V,Q) is called the odd part of Cℓ(V,Q) (it is not a subalgebra). This Z₂-grading plays an important role in the analysis and application of Clifford algebras. The automorphism α is called the main involution or grade involution.

Remark. In characteristic not 2 the algebra Cℓ(V,Q) inherits a Z-grading from the canonical isomorphism with the exterior algebra Λ(V). It is important to note, however, that this is a vector space grading only. That is, Clifford multiplication does not respect the Z-grading only the Z₂-grading. Happily, the gradings are related in the natural way: Z₂ = Z/2Z. The degree of a Clifford number usually refers to the degree in the Z-grading. Elements which are pure in the Z₂-grading are simply said to be even or odd.

If the characteristic of F is not 2 then the even subalgebra Cℓ⁰(V,Q) of a Clifford algebra is itself a Clifford algebra. If V is the orthogonal direct sum of a vector a of norm Q(a) and a subspace U, then Cℓ⁰(V,Q) is isomorphic to Cℓ(U,−Q(a)Q), where −Q(a)Q is the form Q restricted to U and multiplied by −Q(a). In particular over the reals this implies that

$C\ell _{p,q}^{0}(\mathbb {R} )\cong C\ell _{p,q-1}(\mathbb {R} )$ for q > 0, and

$C\ell _{p,q}^{0}(\mathbb {R} )\cong C\ell _{q,p-1}(\mathbb {R} )$for p > 0.

In the negative-definite case this gives an inclusion Cℓ_0,n−1(R) ⊂ Cℓ_{0, n}(R) which extends the sequence

R ⊂ C ⊂ H ⊂ H⊕H ⊂ …

Likewise, in the complex case, one can show that the even subalgebra of Cℓ_n(C) is isomorphic to Cℓ_n−1(C).

Antiautomorphisms

In addition to the automorphism α, there are two antiautomorphisms which play an important role in the analysis of Clifford algebras. Recall that the tensor algebra T(V) comes with an antiautomorphism that reverses the order in all products:

$v_{1}\otimes v_{2}\otimes \cdots \otimes v_{k}\mapsto v_{k}\otimes \cdots \otimes v_{2}\otimes v_{1}$.

Since the ideal I_Q is invariant under this reversal, this operation descends to an antiautomorphism of Cℓ(V,Q) called the transpose or reversal operation, denoted by x^t. The transpose is an antiautomorphism: $(xy)^{t}=y^{t}x^{t}$. The transpose operation makes no use of the Z₂-grading so we define a second antiautomorphism by composing α and the transpose. We call this operation Clifford conjugation denoted ${\bar {x}}$

${\bar {x}}=\alpha (x^{t})=\alpha (x)^{t}.$

Of the two antiautomorphisms, the transpose is the more fundamental.³

Note that all of these operations are involutions. One can show that they act as ±1 on elements which are pure in the Z-grading. In fact, all three operations depend only on the degree modulo 4. That is, if x is pure with degree k then

$\alpha (x)=\pm x\qquad x^{t}=\pm x\qquad {\bar {x}}=\pm x$

where the signs are given by the following table:

k mod 4	0	1	2	3
$\alpha (x)\,$	+	−	+	−	(−1)k
$x^{t}\,$	+	+	−	−	(−1)k(k−1)/2
${\bar {x}}$	+	−	−	+	(−1)k(k+1)/2

The Clifford scalar product

When the characteristic is not 2 the quadratic form Q on V can be extended to a quadratic form on all of Cℓ(V,Q) as explained earlier (which we also denoted by Q). A basis independent definition is

$Q(x)=\langle x^{t}x\rangle$

where <a> denotes the scalar part of a (the grade 0 part in the Z-grading). One can show that

$Q(v_{1}v_{2}\cdots v_{k})=Q(v_{1})Q(v_{2})\cdots Q(v_{k})$

where the v_i are elements of V — this identity is not true for arbitrary elements of Cℓ(V,Q).

The associated symmetric bilinear form on Cℓ(V,Q) is given by

$\langle x,y\rangle =\langle x^{t}y\rangle .$

One can check that this reduces to the original bilinear form when restricted to V. The bilinear form on all of Cℓ(V,Q) is nondegenerate if and only it is nondegenerate on V.

It is not hard to verify that the transpose is the adjoint of left/right Clifford multiplication with respect to this inner product. That is,

$\langle ax,y\rangle =\langle x,a^{t}y\rangle ,$ and

$\langle xa,y\rangle =\langle x,ya^{t}\rangle .$

Structure of Clifford algebras

In this section we assume that the vector space V is finite dimensional and that the bilinear form of Q is non-singular. A central simple algebra over K is a matrix algebra over a (finite dimensional) division algebra with center K. For example, the central simple algebras over the reals are matrix algebras over either the reals or the quaternions.

• If V has even dimension then Cℓ(V,Q) is a central simple algebra over K.
• If V has even dimension then Cℓ⁰(V,Q) is a central simple algebra over a quadratic extension of K or a sum of two isomorphic central simple algebras over K.
• If V has odd dimension then Cℓ(V,Q) is a central simple algebra over a quadratic extension of K or a sum of two isomorphic central simple algebras over K.
• If V has odd dimension then Cℓ⁰(V,Q) is a central simple algebra over K.

The structure of Clifford algebras can be worked out explicitly using the following result. Suppose that U has even dimension and a non-singular bilinear form with discriminant d, and suppose that V is another vector space with a quadratic form. The Clifford algebra of U+V is isomorphic to the tensor product of the Clifford algebras of U and (−1)^dim(U)/2dV, which is the space V with its quadratic form multiplied by (−1)^dim(U)/2d. Over the reals, this implies in particular that

$Cl_{p+2,q}(\mathbb {R} )=M_{2}(\mathbb {R} )\otimes Cl_{q,p}(\mathbb {R} )$

$Cl_{p+1,q+1}(\mathbb {R} )=M_{2}(\mathbb {R} )\otimes Cl_{p,q}(\mathbb {R} )$

$Cl_{p,q+2}(\mathbb {R} )=\mathbb {H} \otimes Cl_{q,p}(\mathbb {R} )$

These formulas can be used to find the structure of all real Clifford algebras.

The Clifford group Γ

In this section we assume that V is finite dimensional and the bilinear form of Q is non-singular.

The Clifford group Γ is defined to be the set of invertible elements x of the Clifford algebra such that

$xv\alpha (x)^{-1}\in V$

for all v in V. This formula also defines an action of the Clifford group on the vector space V that preserves the norm Q, and so gives a homomorphism from the Clifford group to the orthogonal group. The Clifford group contains all elements r of V of nonzero norm, and these act on V by the corresponding reflections that take v to v − <v,r>r/Q(r) (In characteristic 2 these are called orthogonal transvections rather than reflections.)

Many authors define the Clifford group slightly differently, by replacing the action xvα(x)⁻¹ by xvx⁻¹. This produces the same Clifford group, but the action of the Clifford group on V is changed slightly: the action of the odd elements Γ¹ of the Clifford group is multiplied by an extra factor of −1. This action used here has several minor advantages: it is consistent with the usual superalgebra sign conventions, elements of V correspond to reflections, and in odd dimensions the map from the Clifford group to the orthogonal group is onto, and the kernel is no larger than K^*. Using the action α(x)vx⁻¹ instead of xvα(x)⁻¹ makes no difference: it produces the same Clifford group with the same action on V.

The Clifford group Γ is the disjoint union of two subsets Γ⁰ and Γ¹, where Γⁱ is the subset of elements of degree i. The subset Γ⁰ is a subgroup of index 2 in Γ.

If V is finite dimensional with nondegenerate bilinear form then the Clifford group maps onto the orthogonal group of V and the kernel consists of the nonzero elements of the field K. This leads to exact sequences

$1\rightarrow K^{*}\rightarrow \Gamma \rightarrow O_{V}(K)\rightarrow 1,\,$

$1\rightarrow K^{*}\rightarrow \Gamma ^{0}\rightarrow SO_{V}(K)\rightarrow 1.\,$

In arbitrary characteristic, the spinor norm Q is defined on the Clifford group by

$Q(x)=x^{t}x\,$

It is a homomorphism from the Clifford group to the group K^* of non-zero elements of K. It coincides with the quadratic form Q of V when V is identified with a subspace of the Clifford algebra. Several authors define the spinor norm slightly differently, so that it differs from the one here by a factor of −1, 2, or −2 on Γ¹. The difference is not very important.

The nonzero elements of K have spinor norm in the group K^*2 of squares of nonzero elements of the field K. So when V is finite dimensional and non-singular we get an induced map from the orthogonal group of V to the group K^*/K^*2, also called the spinor norm. The spinor norm of the reflection of a vector r has image Q(r) in K^*/K^*2, and this property uniquely defines it on the orthogonal group. This gives exact sequences:

$1\rightarrow \{\pm 1\}\rightarrow Pin_{V}(K)\rightarrow O_{V}(K)\rightarrow K^{*}/K^{*2},\,$

$1\rightarrow \{\pm 1\}\rightarrow Spin_{V}(K)\rightarrow SO_{V}(K)\rightarrow K^{*}/K^{*2}.\,$

Note that in characteristic 2 the group {±1} has just one element.

Spin and Pin groups

In this section we assume that V is finite dimensional and its bilinear form is non-singular. (If K has characteristic 2 this implies that the dimension of V is even.)

The Pin group Pin_V(K) is the subgroup of the Clifford group Γ of elements of spinor norm 1, and similarly the Spin group Spin_V(K) is the subgroup of elements of Dickson invariant 0 in Pin_V(K). When the characteristic is not 2, these are the elements of determinant 1. The Spin group usually has index 2 in the Pin group.

Recall from the previous section that there is a homomorphism from the Clifford group onto the orthogonal group. We define the special orthogonal group to be the image of Γ⁰. If K does not have characteristic 2 this is just the group of elements of the orthogonal group of determinant 1. If K does have characteristic 2, then all elements of the orthogonal group have determinant 1, and the special orthogonal group is the set of elements of Dickson invariant 0.

There is a homomorphism from the Pin group to the orthogonal group. The image consists of the elements of spinor norm 1 ∈ K^*/K^*2. The kernel consists of the elements +1 and −1, and has order 2 unless K has characteristic 2. Similarly there is a homomorphism from the Spin group to the special orthogonal group of V.

In the common case when V is a positive or negative definite space over the reals, the spin group maps onto the special orthogonal group, and is simply connected when V has dimension at least 3. Warning: This is not true in general: if V is R^p,q for p and q both at least 2 then the spin group is not simply connected and does not map onto the special orthogonal group. In this case the algebraic group Spin_p,q is simply connected as an algebraic group, even though its group of real valued points Spin_p,q(R) is not simply connected. This is a rather subtle point, which completely confused the authors of at least one standard book about spin groups.

Spinors

Suppose that p+q=2n is even. Then the Clifford algebra Cℓ_p,q(C) is a matrix algebra, and so has a complex representation of dimension 2ⁿ. By restricting to the group Pin_p,q(R) we get a complex representation of the Pin group of the same dimension, called the spinor representation. If we restrict this to the spin group Spin_p,q(R) then it splits as the sum of two half spin representations (or Weyl representations) of dimension 2^n-1.

If p+q=2n+1 is odd then the Clifford algebra Cℓ_p,q(C) is a sum of two matrix algebras, each of which has a representation of dimension 2ⁿ, and these are also both representations of the Pin group Pin_p,q(R). On restriction to the spin group Spin_p,q(R) these become isomorphic, so the spin group has a complex spinor representation of dimension 2ⁿ.

More generally, spinor groups and pin groups over any field have similar representations whose exact structure depends on the structure of the corresponding Clifford algebras: whenever a Clifford algebra has a factor that is a matrix algebra over some division algebra, we get a corresponding representation of the pin and spin groups over that division algebra. For examples over the reals see the article on spinors.

Applications

Differential geometry

One of the principal applications of the exterior algebra is in differential geometry where it is used to define the bundle of differential forms on a smooth manifold. In the case of a (pseudo-)Riemannian manifold, the tangent spaces come equipped with a natural quadratic form induced by the metric. Thus, one can define a Clifford bundle in analogy with the exterior bundle. This has a number of important applications in Riemannian geometry.

Physics

Clifford algebras have numerous important applications in physics. Physicists usually consider a Clifford algebra to be an algebra spanned by matrices γ₁,…,γ_n called Dirac matrices which have the property that

$\gamma _{i}\gamma _{j}+\gamma _{j}\gamma _{i}=2\eta _{ij}\,$

where η is the matrix of a quadratic form of signature (p,q) — typically (1,3) when working in Minkowski space. These are exactly the defining relations for the Clifford algebra Cl_1,3(C) (up to an unimportant factor of 2), which by the classification of Clifford algebras is isomorphic to the algebra of 4 by 4 complex matrices.

The Dirac matrices were first written down by Paul Dirac when he was trying to write a relativistic first-order wave equation for the electron, and give an explicit isomorphism from the Clifford algebra to the algebra of complex matrices. The result was used to define the Dirac equation. The entire Clifford algebra shows up in quantum field theory in the form of Dirac field bilinears.

Footnotes

1. Mathematicians who work with real Clifford algebras and prefer positive definite quadratic forms (especially those working in index theory) sometimes use a different choice of sign in the fundamental Clifford identity. That is, they take v² = −Q(v). One must replace Q with −Q in going from one convention to the other.
2. The opposite is true when uses the alternate (−) sign convention for Clifford algebras: it is the conjugate which is more important. In general, the meanings of conjugation and transpose are interchanged when passing from one sign convention to the other. For example, in the convention used here the inverse of a vector is given by $v^{-1}=v^{t}/Q(v)$ while in the (−) convention it is given by $v^{-1}={\bar {v}}/Q(v)$.

References

• Carnahan, S. Borcherds Seminar Notes, Uncut. Week 5, "Spinors and Clifford Algebras".
• Lawson and Michelsohn, Spin Geometry, Princeton University Press. 1989. ISBN 0-691-08542-0. An advanced textbook on Clifford algebras and their applications to differential geometry.
• Lounesto, P., Clifford Algebras and Spinors, Cambridge University Press. 2001. ISBN 0-521-00551-5.
• Porteous, I., Clifford Algebras and the Classical Groups, Cambridge University Press. 1995. ISBN 0-521-55177-3.

External links

• Planetmath entry on Clifford algebras
• A history of Clifford algebras (unverified)

Shear and Slope

The first terms needed are triangle, base, vertex, and area. For instance, the proposition that for a triangle of given base and area, the locus of the vertex is a line parallel to the base. Imagine that the vertex is dragged along this line, deforming the triangle. Imagine also that the whole plane is similarly deformed by a transformation taking lines to lines. This transformation is a shear mapping.

The shear mapping is expressed as a linear transformation:

$(t,x){\begin{pmatrix}1&v\\0&1\end{pmatrix}}=(t,tv+x).$

Here it is written in the kinetic interpretation with a vertical (x) space axis as time (t) evolves horizontally, such as used in time series studies.

At t=1 the shear has transformed (1,0) to (1,v), the point where a slope v line intersects t=1. Thus the parameter v in the shear transformation can be called slope.

The rectangles given by constant t and x are transformed by the shear to parallelograms, but the area of one of these parallelograms equals the area of the rectangle before transformation. Thus shear transformations preserve area.

Let $e={\begin{pmatrix}0&1\\0&0\end{pmatrix}}$ and note that e² = 0, the zero matrix, and that the shear matrix is ve plus the identity matrix. Dual numbers are used in abstract algebra to provide a short-hand for the matrix subalgebra ${\begin{pmatrix}a&b\\0&a\end{pmatrix}}:$

Definition: $N=\{a+be:a,b\in R,\ e^{2}=0\}$ is the set of dual numbers. The basis {1,e} characterizes it as a 2-algebra over R. If z = a+be, let z* = a−be, a conjugate. Then

$(a+be)(a-be)=a^{2}$ since e² = 0.

Note that zz* = 1 implies z = ± 1 + be for some b in R. Furthermore, exp(be) = 1 + be since the exponential series is truncated after two terms when applied to the e-axis. Consequently the logarithm of 1 + ve is v. Thus v can be considered the angle of 1+ve in the same way that the logarithm of a point on the unit circle is the radian angle of the point, as in Euler’s formula (exp and log are inverses).

The shear mappings acting on the plane form a multiplicative group that is isomorphic to the additive group of real numbers.

The three angles

In Euclidean plane geometry there is the trichotomy right angle, acute angle, obtuse angle. Here a trichotomy of linear motions distinguishes three species of angle.

Each of the angles pivots on its peculiar motion: rotation for circular angle, squeeze mapping for hyperbolic angle, and shear for the slope. Furthermore, each motion evolves into its peculiar algebra of complexity: the dual numbers for shear, the split-binarions for hyperbolic angle, and the rotation and circular angle correspond to the plane of division binarions, called "complex numbers" by some. In fact, in the sense of a real 2-algebra, "complex" is ambiguous: each of the division binarions, split-binarions, and dual numbers forms a plane of "complex numbers".

A property of arc length on a circle is that it stays the same under rotation. It is said that "arc length is an invariant of rotation." A segment on t=1 that is transformed by a shear has the same length after the shear as before. Similarly, a hyperbolic angle is invariant under a squeeze. These three invariances can be seen together as consequences of area-invariance of the three motions: The hyperbolic angle is the area of the corresponding hyperbolic sector to xy=1, which has minimal radius √2 to (1,1). A circular angle corresponds to the area of its sector in a circle of radius √2. Finally, the slope is equal to the area of the triangle with base on t= √2 and hypotenuse corresponding to the slope. Since squeeze, shear, and rotation are all area-preserving, their motions in their corresponding planes preserve the central angles there. The traditional term for study of angle-preservation is conformal mapping, often presuming circular angles.

These three species of angle provide a parameter for polar coordinates in each of the three 2-algebras found as subspaces of 2 × 2 real matrices.

Quaternions

The algebra of Quaternions is a structure first studied by the Irish mathematician William Rowan Hamilton which extends the two-dimensional complex numbers to four dimensions. Multiplication is non-commutative in quaternions, a feature which enables its representation of three-dimensional rotation. Hamilton's provocative discovery of quaternions founded the field of hypercomplex numbers. Suggestive methods like dot products and cross products implicit in quaternion products enabled algebraic description of geometry now widely applied in science and engineering.

Definitions

Quaternion plaque on Broom Bridge, Dublin, which says:

Here as he walked by
on the 16th of October 1843
Sir William Rowan Hamilton
in a flash of genius discovered
the fundamental formula for
quaternion multiplication i² = j² = k² = ijk = −1 & cut it on a stone of this bridge

A Quaternion corresponds to an ordered 4-tuple $q=(a,b,c,d)$, where $a,b,c,d\in \mathbb {R}$. A quaternion is denoted $q=a+bi+cj+dk$. The sum $bi+cj+dk$ is called the vector part of q, and a is the real part. Hamiltion coined the term vector in this context. Subsequent developments have extended the usage of the term vector to any element of a linear space. The vectors in H form a 3-dimensional subspace V.

The set of all quaternions is denoted by $\mathbb {H}$. It is straightforward to define component-wise addition and scalar multiplication on $\mathbb {H}$, making it a real vector space.

Multiplication follows the rules of the "quaternion group" Q₈ = {1, -1, i, -i, j, -j, k, -k} that Hamilton carved into a stone of Broom Bridge, Dublin:

$i^{2}=j^{2}=k^{2}=ijk=-1$

The rules for the pairwise multiplication of $i$, $j$, and $k$ are:

$ij=k,\ \ jk=i,\ \ ki=j$ (positive cyclic products)

$ji=-k,\ \ kj=-i,\ \ ik=-j$ (negative cyclic products).

Using these, one can define a general rule for multiplication of quaternions. Because quaternion multiplication is not commutative, $\mathbb {H}$ is a not a field. However, every nonzero quaternion has a multiplicative inverse (see below), so the quaternions are an example of a division ring. It is important to note that the non-commutative nature of quaternion multiplication makes it impossible to define the quotient $p/q$ of two quaternions p and q unambiguously, as the quantities $pq^{-1}$ and $q^{-1}p$ are generally different.

Like the more familiar complex numbers, the quaternions have a conjugation, often denoted by a superscript star: $q^{*}$. The conjugate of the quaternion $q=a+bi+cj+dk$ is $q^{*}=a-bi-cj-dk$. As is the case for the complex numbers, the product $qq^{*}$ is always a positive real number equal to the sum of the squares of the quaternion's components. The norm of a quaternion is the square root of $qq^{*}$.

If pq is the product of two quaternions, then $(pq)(pq)^{*}=(pp^{*})(qq^{*}),$ implying that $\mathbb {H}$ forms a composition algebra.

The multiplicative inverse of a non-zero quaternion $q$ is given by

$q^{-1}={\frac {q^{*}}{qq^{*}}}$ where division is defined since $qq^{*}\neq 0.$

Unlike in the complex case, the conjugate $q^{*}$ of a quaternion $q$ can be computed algebraically:

$q^{*}=-{\frac {1}{2}}(q+iqi+jqj+kqk)$.

Versors and elliptic space

William Kingdon Clifford used Hamilton’s quaternions to explicate rotation geometry as an elliptic space with its own variety of lines, parallels, and surfaces. The ideas were reviewed in 1948 by Lemaitre and Coxeter and that sketch has these definitions:

A versor is a quaternion of norm one, thus it lies on a 3-dimensional sphere found in the 4-space of quaternions. The versors are given by Euler's formula for complex numbers where the imaginary unit is taken from the unit sphere in the 3-space of vector quaternions:

$v=\cos c+s\sin c=e^{cs},\ \ s^{2}=-1.$

The distance between two versors u and v is $d(u,v)=\arccos(uv^{*}+vu^{*})/2.$

A right parataxy on elliptic space is effected by multiplying on the right by a versor $v=e^{cs}.$ Similarly a left parataxy arises from left multiplication. In recognition of his contribution to elliptic geometry, a parataxy is called a Clifford translation.

The general displacement of elliptic space is a combination of two parataxies, one left, one right:$x\mapsto uxv.$ Note that if $u=v^{*},$ then the real line in the quaternions is fixed and the displacement is a rotation of the 3-space of quaternion vectors.

The term line is appropriated for elliptic geometry. These lines are not straight, but they are parametrized by real numbers. Each line is associated with a right versor like s when c = π/2 in v. Then $L=\{e^{cs}:c\in R\}$ is a typical elliptic line. It corresponds to the axis of the rotation

$x\mapsto e^{cs}xe^{-cx}.$

Now for u not on L, there are two Clifford parallels to L through u:

$\{ue^{cs}:c\in R\},\quad \{e^{cs}u:c\in R\}.$

For fixed right versors r and s, a Clifford surface can be formed as a union of Clifford parallels or as

$\{e^{cs}e^{dr}:b,c\in R\}.$

To form elliptic space from versors, two versors u and v are equivalent if u + v = 0. Modulo this equivalence, the versors, their algebra and geometry, represent elliptic space.

Linear viewpoint

Quaternions may be represented by 2×2 matrices with complex number entries: the place of $i,j,k$ is taken by these arrays:

${\begin{pmatrix}i&0\\0&-i\end{pmatrix}},\quad {\begin{pmatrix}0&1\\-1&0\end{pmatrix}},\quad {\begin{pmatrix}0&i\\i&0\end{pmatrix}}.$

One uses matrix multiplication to verify that these expressions obey the rules of presentation of Q₈.

M(2,C) denotes the full algebra of 2×2 complex matrices, which has eight real dimensions, and sustains a representation of $\mathbb {H}$ as a four-dimensional subalgebra. The linear properties of $\mathbb {H}$ and M(2,C) assure the fidelity of the representation once the copy of Q₈ has been identified.

Quaternions, like other associative hypercomplex systems of the 19th century, eventually were viewed as matrix algebras in the 20th century. However, in 1853 Hamilton included biquaternions in his book of Lectures on Quaternions.

Biquaternions are quaternions with complex number coefficients, sometimes called complex quaternions. Biquaternions form an algebra isomorphic to M(2,C). If the rows or columns of a matrix are proportional, then the determinant is zero, and there is no inverse. Nevertheless, such matrices have been used in physical science to represent events on a light-path from the origin. Authors Silberstein and Lanczos refer to this algebra as the biquaternions, but other writers have abandoned the label: Elie Cartan used M(2,C) extensively in The Theory of Spinors (1938), and Wolfgang Pauli, in his matrix mechanics of the atom, caused himself to be associated with M(2,C).

Pauli Spin Matrices

Quaternions are closely related to the Pauli spin matrices of Quantum Mechanics. The Pauli matrices are often denoted as

$\sigma _{1}={\begin{pmatrix}0&1\\1&0\end{pmatrix}}$ , $\sigma _{2}={\begin{pmatrix}0&-i\\i&0\end{pmatrix}}$ , $\sigma _{3}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}$

(Where $i$ is the well known quantity ${\sqrt {-1}}$ of complex numbers)

The 2×2 identity matrix is sometimes taken as $\sigma _{0}$.

Thus $S$, the real linear span of the matrices $\sigma _{0}$, $i\sigma _{1}$, $i\sigma _{2}$ and $i\sigma _{3}$, is isomorphic to $\mathbb {H}$. For example, take this matrix product:

${\begin{pmatrix}i&0\\0&-i\end{pmatrix}}{\begin{pmatrix}0&1\\-1&0\end{pmatrix}}={\begin{pmatrix}0&i\\i&0\end{pmatrix}}$

Or, equivalently,   $i\sigma _{3}\ i\sigma _{2}=i\sigma _{1}.$

All three of these matrices square to the negative of the identity matrix. If we take $1=\sigma _{0}$, $i=i\sigma _{3}$, $j=i\sigma _{2}$, and $k=i\sigma _{1}$, it is easy to see that the span of the these four matrices is "the same as" (that is, isomorphic to) the set of quaternions $\mathbb {H}$.

Exercises

1. Using the presentation equations of Q₈, write out the full product of two quaternions. In other words, given $q_{1}=a_{1}+b_{1}i+c_{1}j+d_{1}k$ and $q_{2}=a_{2}+b_{2}i+c_{2}j+d_{2}k$, find the components of their product $q=q_{1}q_{2}.$
2. Show the composition algebra property $(pq)(pq)^{*}=(pp^{*})(qq^{*}).$ Hint: use w: Euler's four-square identity.

Axial pencils

The axis of a pencil is the real axis in the 4-algebra

Hamilton's quaternions provide a picture of a pencil of complex number planes that fill out his hyperspace. Another pair of pencils provide alternative descriptions of 4-space as made up of planar algebras: The hyperspace is $\mathbb {R} ^{4}$ with the first coordinate taken as the real line, and as the axis of the various pencils. The Hamilton case uses the sphere of imaginary units

$S^{2}=\{q\in H:q^{2}=-1\}=\{xi+yj+zk:x^{2}+y^{2}+z^{2}=1\}.$

Any pair of antipodal points on this sphere generates a plane isomorphic to the ordinary complex plane $\mathbb {C} .$

The second and third pencils derive from the findings of James Cockle and Arthur Cayley. Cayley set up an arithmetic of matrix multiplication which has expedited modern science. For instance, the so-called imaginary units are represented by ${\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$ which has multiplicative square equal to the negative of the identity matrix. But then there is also by ${\begin{pmatrix}0&1\\1&0\end{pmatrix}}$ which generates an algebraic plane distinct from ordinary complex numbers. This algebra split-binarions, has inverse proportion included as a structural feature, such as found in economics or spacetime. In fact, the Lorentz boost is exhibited by a split-binarion multiplication. The inherent relation was recognized in the 19th century by J. Cockle, W.K. Clifford, and A. Macfarlane in the English world and by some Serbians.

The second pencil is an imaginary one without linear representation. As Hamilton had a sphere of imaginary units, Macfarlane would have a sphere of hyperbolic units u with u² = +1. The full algebra of split-binarions is $A=\{q=x+yu:x,y\in \mathbb {R} \}$ Any pair of elements that are polar opposite on this sphere generate a plane isomorphic to the split-binarions A. The 4-algebra containing this pencil is the hyperbolic quaternion algebra. As Oliver Heaviside and Willard Gibbs advocated a positive dot product for vectors, they have been associated with hyperbolic quaternions. When this algebra drew attention in the 1890s a "great vector debate" ensued in various publications including Nature. When the failure of the algebra to satisfy the associative law of multiplication was noted, it was realized that no matrix representation would be found.

Each plane of the pencil can represent a Lorentz boost. However, rotations of the vector subspace, an operation within the reach of Hamilton's structure, is beyond the means of hyperbolic quaternions, hence the Lorentz group cannot be represented with Macfarlane's algebra.

The third pencil arises from both imaginary units and hyperbolic units as found in the ring of 2x2 real matrices. In this figure there must be noted nilpotent matrices such as by ${\begin{pmatrix}0&1\\0&0\end{pmatrix}}$ which correspond to dual numbers in the matrix algebra. Such planes separate the complex and split-binarion planes, and are included in the pencil. The axis of the pencil is the line of matrices that are real multiples of the identity matrix. Over an alternate basis this ring is known as split-quaternions, and the pencil has three types of planar subrings.

2x2 real matrices

The associative algebra of 2×2 real matrices is denoted by M(2, R). Two matrices p and q in M(2, R) have a sum p + q given by matrix addition. The product matrix p q is formed through matrix multiplication. For

$q={\begin{pmatrix}a&b\\c&d\end{pmatrix}},$ let

$q^{*}={\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}.$

Then q q^* = q^* q = (ad − bc) I, where I is the 2×2 identity matrix. The real number ad − bc is called the determinant of q. When ad − bc ≠ 0, then q is an invertible matrix, and

$q^{-1}={\frac {q^{*}}{ad-bc}}.$

The collection of all such invertible matrices constitutes the general linear group GL(2, R). In the terms of abstract algebra, M(2, R) with the associated addition and multiplication operations forms a ring, and GL(2, R) is its group of units. M(2, R) is also a four-dimensional vector space, so it is also an associative algebra.

The 2×2 real matrices are in one-one correspondence with the linear mappings of the two-dimensional Cartesian coordinate system into itself by the rule

$(x,\ y)\mapsto (x,\ y){\begin{pmatrix}a&c\\b&d\end{pmatrix}}=(ax+by,\ cx+dy).$

M(2,R) is where all three types of planar angle come to common expression in terms of area. M(2,R) is described as a pencil on a real line that is shared by three types of 2-algebras appearing as subalgebras of M(2,R). They are the division binarions, split-binarions, and dual numbers which use circular angle, hyperbolic angle, and slope, respectively.

The hyperbolic angle is defined in terms of area under y=1/x. The circular angle equals the area of the corresponding sector of a circle of radius √2. Likewise, the slope equals the area of a triangle with base on a line and apex at a point √2 distance from the line.

The angles have the feature of invariance under motion, according to the type of plane. Either a rotation, a squeeze, or a shear as the case may be. Generalization of the notion of imaginary unit in M(2,R) is addressed first. It is matrix multiplication that produces the group action on a plane, so the characteristic of matrices that makes them preservers of area is addressed next.

Pencil of planar subalgebras

In synthetic geometry, the term pencil is used for the set of lines on a given point, and axial pencil for the set of planes on a given line. Here the axis is the set of multiples of the identity matrix I by real numbers. Every matrix that is not in this set is contained in a unique planar subalgebra. These subalgebras are division-binarions, split-binarions, or dual numbers.

Given a matrix m with m² in {I, 0, −I}, there is a subalgebra

$P_{m}=\{xI+ym:x,y\in \Re \}.$

Then P_m is a commutative subalgebra and M(2, R) = ⋃P_m  where the union is over all m such that m² ∈ {−I, 0, I }.

To identify such m, first square the generic matrix:

${\begin{pmatrix}aa+bc&ab+bd\\ac+cd&bc+dd\end{pmatrix}}.$

When a + d = 0 this square is a diagonal matrix.

Thus one assumes d = −a when looking for m to form commutative subalgebras. When mm = −I, then bc = −1 − aa, an equation describing a hyperbolic paraboloid in the space of parameters (a,b,c). Such an m serves as an imaginary unit. In this case P_m is isomorphic to the division binarions, also known as the field of (ordinary) complex numbers.

When mm = +I, m is an involutory matrix. Then bc = +1 − aa, also giving a hyperbolic paraboloid. If a matrix is an idempotent matrix, it must lie in such a P_m and in this case P_m is ring isomorphic to split-binarions.

The case of a nilpotent matrix, mm = 0, arises when only one of b or c is non-zero, and the commutative subalgebra P_m is then a copy of the dual number plane.

When M(2, R) is reconfigured with a change of basis, this pencil is seen in split-quaternions where the sets of square roots of I and −I take a symmetrical shape as hyperboloids.

Equi-areal mapping

First transform one differential vector into another:

$(du,\ dv)=(dx,\ dy){\begin{pmatrix}p&q\\r&s\end{pmatrix}}=(p\ dx+r\ dy,\ \ q\ dx+s\ dy).$

Areas are measured with density $dx\wedge dy$, an exterior product for which $dx\wedge dx=0=dy\wedge dy.$ In linear mapping this differential 2-form is transformed:

${\begin{aligned}du\wedge dv&=(p\ dx+r\ dy)\wedge (q\ dx+s\ dy)\\&=0+ps\ dx\wedge dy+qr\ dy\wedge dx+0\\&=(ps-qr)\ dx\wedge dy\\&=\det(g)\ dx\wedge dy.\end{aligned}}$

Area is preserved when the determinant is one. Thus the equi-areal mappings are identified with $SL(2,\mathbb {R} )=\{g\in M(2,\mathbb {R} ):\det(g)=1\},$ the special linear group. Given the profile above, every such g lies in a commutative subring P_m representing a type of complex plane according to the square of m. Since g g* = I, one of the following three alternatives occurs:

• mm = −I and g is a Euclidean rotation, or
• mm = I and g is a hyperbolic rotation, or
• mm = 0 and g is a shear mapping.

The preservation of area provides a common foundation for study of conformal mapping in a plane. In fact, there are three species of angle used in analysis, circular and hyperbolic angle and slope as an expression of angle in the dual number plane.

Functions of 2 × 2 real matrices

The commutative subalgebras of M(2, R) determine the function theory; in particular the three types of subalgebras each have their own algebraic structures which set the value of algebraic expressions. Consideration of the square root function and the logarithm function serves to illustrate the constraints implied by the special properties of each type of subalgebra P_m in the above pencil.

First note that the invertible elements, the units, of each plane form a topological group with one, two, or four components. The component that contains 1 is called the component of the identity. The polar coordinates of an element include an angle factor:

• If mm = −I, then z = ρ exp(θm) where θ is a circular angle.
• If mm = 0, then z = ρ exp(sm) or z = −ρ exp(sm) where s is a slope.
• If mm = I, then z = ρ exp(a m) or z = −p exp(a m) or

z = m ρ exp(a m) or z = −m ρ exp(a m) where a is a hyperbolic angle.

In the first case exp(θ m) = cos(θ) + m sin(θ), known as Euler's formula.

In the case of the dual numbers exp(s m) = 1 + s m. Finally, in the case of split-binarions there are four components in the group of units. The identity component is parameterized by ρ and exp(a m) = cosh(a) + m sinh(a).

Now ${\sqrt {\rho \ \exp(am)}}={\sqrt {\rho }}\ \exp \left({\frac {1}{2}}am\right)$ regardless of the subalgebra P_m, but the argument of the function must be taken from the identity component of its group of units. Half the plane is lost in the case of the dual number structure; three-quarters of the plane must be excluded in the case of the split-binarions.

Similarly, if ρ exp(a m) is an element of the identity component of the group of units of a plane associated with 2×2 matrix m, then the logarithm function results in a value log ρ+ a m. The domain of the logarithm function suffers the same constraints as does the square root function described above: half or three-quarters of P_m must be excluded in the cases mm = 0 or mm = I.

2 × 2 real matrices as species of complex numbers

Every 2×2 real matrix can be interpreted as one of three species of (generalized) complex number: a division binarion, a dual number, or a split-binarion. Above, the algebra of 2×2 matrices is profiled as a union of subalgebras P_m, all sharing the same real axis. One can determine to which type of subalgebra a given 2×2 matrix belongs as follows:

Consider the 2×2 matrix

$z={\begin{pmatrix}a&b\\c&d\end{pmatrix}}.$

The subalgebra P_m containing z is found by projections:

As noted above, the square of the matrix z is diagonal when a + d = 0. The matrix z must be expressed as the sum of a multiple of the identity matrix I and a matrix in the hyperplane a + d = 0. Projecting z alternately onto these subspaces of R⁴ yields

$z=xI+n,\quad x={\frac {a+d}{2}},\quad n=z-xI.$

Furthermore,

$n^{2}=pI$ where $p={\frac {(a-d)^{2}}{4}}+bc$.

Now z is n one of three species of subalgebra:

• If p < 0, then it is a division binarion:

  Let $q=1/{\sqrt {-p}},\quad m=qn$. Then $m^{2}=-I,\quad z=xI+m{\sqrt {-p}}$.

• If p = 0, then it is the dual number:

  $z=xI+n$.

• If p > 0, then z is a split-binarion:

  Let $q=1/{\sqrt {p}},\quad m=qn$. Then $m^{2}=+I,\quad z=xI+m{\sqrt {p}}$.

Similarly, a 2×2 matrix can also be expressed in polar coordinates with the caveat that there are two connected components of the group of units in the dual number plane, and four components in the split-binarion plane.

Projective group

A given 2 × 2 real matrix with ad ≠ bc acts on projective coordinates [x : y] of the real projective line P(R) as a linear fractional transformation:

$[x:y]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ =\ [ax+by:\ cx+dy].$ When cx + dy = 0, the image point is the point at infinity, otherwise

$[ax+by:\ cx+dy]\ \thicksim \left[{\frac {ax+by}{cx+dy}}:\ 1\right].$

Rather than acting on the plane as in the section above, a matrix acts on the projective line P(R), and all proportional matrices act the same way.

Let p = ad – bc ≠ 0. Then

${\begin{pmatrix}a&c\\b&d\end{pmatrix}}\times {\begin{pmatrix}d&-c\\-b&a\end{pmatrix}}\ =\ {\begin{pmatrix}p&0\\0&p\end{pmatrix}}.$

The action of this matrix on the real projective line is

$[x:y]{\begin{pmatrix}p&0\\0&p\end{pmatrix}}\ =\ [px:py]\thicksim [x:y]$ because of projective coordinates,

so that the action is that of the identity mapping on the real projective line. Therefore,

${\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ {\text{and}}\ {\begin{pmatrix}d&-c\\-b&a\end{pmatrix}}$ act as multiplicative inverses.

The projective group starts with the group of units GL(2,R) of M(2,R), and then relates two elements if they are proportional, since proportional actions on P(R) are identical: PGL(2,R) = GL(2,R)/~ where ~ relates proportional matrices. Every element of the projective linear group PGL(2,R) is an equivalence class under ~ of proportional 2 × 2 real matrices.

Autonomous differential equation

The differential equation $f^{\prime }=af$ has solution $f(t)=\exp(at)+C,$ where a is a given constant and C is an arbitrary constant.

Using division binarions, the equation $f^{\prime }=af$ may be interpreted as a tangent slope to a curve parametrized by t : for i² = − 1, the differential equation $f^{\prime }=aif$ has solution $f(t)=\exp(ait)+C.$

Similarly, for j² = +1, the differential equation $f^{\prime }=ajf$ has solution $f(t)=\exp(ajt)=\cosh at+j\sinh at,$ a branch of the unit hyperbola.

In the autonomous differential equation $f^{\prime }=Af,$ the matrix A corresponds to a constant binarion that relates the slope of the tangent and the curve. The solution of the matrix differential equation is given by the exponential function, using this constant as a cofactor in the argument. The solution is periodic when the constant is a division binarion, and not when it is a split-binarion. Evidently the constant also determines which subalgebra of M(2,R) contains the solution curve.

Whereas linear algebra is premised on simultaneous linear equations, there is the existence theorem for solution of a system of differential equations

${\frac {du_{i}}{dt}}=\sum _{k=1}^{p}c_{ik}u_{k}\quad (i=1,...p)\quad {\text{where the}}\quad c_{ik}$ are continuous functions.

Here p = 2, the matrix is constant, and the solution is exhibited. However, some notational gymnastics are expected of the mathematical reader. Following tradition, the matrix is written to the left and function notation is employed. So rather than row vectors fed into the matrix in previous sections, the function is read as a column vector, which the reader must reconstruct from a binarion:

References

• w:Rafael Artzy (1965) Linear Geometry, Chapter 2-6 Subgroups of the Plane Affine Group over the Real Field, p. 94, Addison-Wesley.
• Helmut Karzel & Gunter Kist (1985) "Kinematic Algebras and their Geometries", found in
  • Rings and Geometry, R. Kaya, P. Plaumann, and K. Strambach editors, pp. 437–509, esp 449,50, D. Reidel, ISBN 90-277-2112-2 .
• Svetlana Katok (1992) Fuchsian groups, pp. 113ff, University of Chicago Press ISBN 0-226-42582-7 .
• Garret Sobczyk (2012). "Chapter 2: Complex and Hyperbolic Numbers". New Foundations in Mathematics: The Geometric Concept of Number. Birkhäuser. ISBN 978-0-8176-8384-9.

Hypercomplex numbers

The terms group theory and ring theory are refinements of algebraic understanding that developed in the era of electronics and aircraft, the 20th century. The term hypercomplex number harkens back to the age of steam. For the most part, the hypercomplex systems have been assimilated through the resolution of vision provided by groups, rings, and fields, and the term has been retired from use other than historic reference. Similarly, the field of complex numbers $C=\{z=x+iy,\ x,y\in R\},\ i^{2}=-1,$ has an insufficiently descriptive name, and might be better described as division binarions C according to composition algebra theory.

W.R. Hamilton (1805−1865) studied quaternions and biquaternions

Hypercomplex numbers grew out of William Rowan Hamilton's construction of quaternions in the 1840s. The legacy of his vision continues in spatial vector algebra: for vectors $v=ai+bj+ck$ and $w=di+ej+fk,$ the well-known products are

• Dot: $v\cdot w=ad+be+cf\in R$
• Cross: $v\times w=(bf-ec)i-(af-dc)j+(ae-db)k\in R^{3}.$

These products are the severed remnants of Hamilton’s quaternion product: $\ \ vw=-v\cdot w+v\times w\in R^{4}.$

In 1845 John T. Graves and Arthur Cayley described an eight-dimensional hypercomplex system now referred to as octonions or Cayley numbers. They extend quaternions but associativity of multiplication is lost. James Cockle challenged the presumption of quaternions in four dimensions by presenting associative hypercomplex systems tessarines (1848) and coquaternions (1849). Hamilton had his own eight-dimensional system (biquaternions) that were explored in his Lectures on Quaternions (1853), but virtually ignored in Elements of Quaternions (completed by his son in 1865) and in the version edited by Charles Jasper Jolly in 1899.

Quaternions feature the property of anti-commutativity of the basis vectors i, j, k:

$ij=-ji=k,\quad jk=-kj=i,\quad ki=-ik=j.$ (in coquaternions $jk=-kj=-i$).

Due to anti-commutativity, squaring a vector leaves many cancelled terms:

$(ai+bj+ck)^{2}=-a^{2}-b^{2}-c^{2},$   thus for $r=ai+bj+ck,$

$(a^{2}+b^{2}+c^{2}=1)\ \equiv \ (r^{2}=-1).$

For any such r, the plane {x + y r : x,y in R} is a complex number plane, and by Euler's formula the mapping $ar\mapsto \cos a+r\sin a$ takes the ray through r to a wrapping of the unit circle in that plane. The unit sphere in quaternions is composed of these circles, considering the variable r. According to Hamilton, a unit quaternion is a versor; evidently every versor can be known by its parameters a and r.

W.K. Clifford (1845−1879) studied split-biquaternions

When the anti-commutativity axiom is changed to commutativity, then two square roots of minus one, say h and i, have a product hi with square $(hi)^{2}=hihi=h^{2}i^{2}=(-1)(-1)=+1.$ James Cockle’s tessarines are based on such an imaginary unit, now with plus one for its square. Cockle initiated the use of  j, j² = +1, to represent this new imaginary unit that is not a square root of minus one. The tessarines are z = w + z j where z, w are in C. The real tessarines $D=\{a+bj:a,b\in R\}$ feature a unit hyperbola, contrasting with the unit circle $\{a+bi:a^{2}+b^{2}=1\}\subset C.$ Whereas the circle surrounds the origin, a hyperbola has radii in only half of the directions of the plane and requires a conjugate hyperbola to cover the other half, and even then the asymptotes, that they share, provide even more directions in the plane. In 1873 William Kingdon Clifford exploited the real tessarines to modify Hamilton's biquaternions: where Hamilton had used elements of C (division binarions) for coefficients of a biquaternion q = w + x i + y j + z k, Clifford used real tessarines (now called split-binarions D). Clifford’s construction illustrated a process of generating new algebras from given ones in a procedure called tensor products: Hamilton’s biquaternions are $C\otimes H$, and the split biquaternions of Clifford are $D\otimes H.$

Clifford was precocious, particularly in his anticipation of a geometric model of gravitation as hills and valleys in a temporal plenum. But he lived before set theory, modern logical and mathematical symbology, and before abstract algebra with its firmament of groups, rings and fields. One of the realities of light is its finite speed: a foot per nanosecond, an astronomic unit in 500 seconds, or a light year in a year. When a diagram uses any of these pairs of units as axes, the diagonals through the origin represent the locus of light, one for the left beam, one for the right. The diagonals are asymptotes to hyperbolas, such as $aj\mapsto \cosh a+j\sinh a,$ a real tessarine. Eventually, over decades of deliberation, physicists realized that this hyperbola was the answer to a linear-velocity problem: How can v + w be the sum of two velocities when such accumulation may run over the speed of light?

The hyperbola lies between the asymptotes and will not run over the speed of light. In the real tessarine system the points of the hyperbola are $e^{aj}$ and $e^{bj},$ representing two velocities in the group $\{e^{xj}:x\in R\},$ a hyperbola. The sum of two velocities is found by their product $e^{aj}e^{bj}=e^{(a+b)j},$ another element of the hyperbola. After 1911, the parameter a was termed rapidity. Evidently this aspect of special relativity was born of real tessarines.

The electromagnetic work of Clerk-Maxell and Heinrich Hertz demanded a fitting context for theorizing with the temporal variable included. Maxwell had used Hamilton’s del operator

$\nabla =i{\frac {\partial }{\partial x}}+j{\frac {\partial }{\partial y}}+k{\frac {\partial }{\partial z}}$ in A Treatise on Electricity and Magnetism,

but the quaternion algebra is unsuitable: it is implicitly a Euclidean 4-space since $qq^{*}=w^{2}+x^{2}+y^{2}+z^{2},$ the square of the Euclidean norm.

Alex Macfarlane (1851−1913) studied hyperbolic quaternions

In the 1890s Alexander Macfarlane advocated Space Analysis with a hypercomplex system that exchanged Hamilton's sphere of imaginary units for a sphere of Cockle's imaginary units that square to +1. He retained the anti-commutative property of quaternions so that $qq^{*}=w^{2}-x^{2}-y^{2}-z^{2}.$ Then in this system of hyperbolic quaternions, for any r on the sphere, $\{x+yr:x,y\in R\}$ is a plane of split binarions, including unit hyperbola suitable to represent motion at any rapidity in direction r. The hyperbolic quaternions looked like an elegant model for electromechanics until it was found wanting. The problem was that the simple property of associative multiplication broke down in hyperbolic quaternions, and though it was a hypercomplex system with a useful model, loss of this property put it outside the purview of group theory, for instance.

Once the axioms of a vector space were established, hypercomplex systems were included. The axioms require a commutative group of vectors, a scalar field, and rules of operations. Putting the axioms of a vector space together with those for a ring establishes the meaning of an algebra in the study of abstract algebra.

For associative hypercomplex systems, Joseph Wedderburn removed all the mystery in 1907 when he showed that any such system could be represented with matrix rings over a field. For instance, 2 x 2 real matrices form an algebra M(2,R) isomorphic to coquaternions and 2 x 2 complex matrices form an algebra M(2,C) isomorphic to biquaternions. These algebras, along with R, C and tessarines form the associative composition algebras which are noted for the property

$(pq)(pq)^{*}=(pp^{*})(qq^{*}).$

About 1897 four cooperative efforts changed mathematics for the better. Giuseppe Peano began to assemble his Formulario Mathematico, Felix Klein spearheaded the mathematical encyclopedia project, the quadrennial series of International Congresses of Mathematics was begun, and the International Association for Promoting the Study of Quaternions and Allied Systems of Mathematics published a bibliography and annual review.

Peano's effort gave mathematicians the symbolic language to compress concepts and proofs using set theory. Klein's encyclopedia upheld German as the primary medium, and the Congresses drew together all nations. The Quaternion Society was the primary arena addressing hypercomplex numbers, and was dissolved after 1913 upon the death of its president, Alexander Macfarlane.

Hypercomplex number systems

The best-known hypercomplex number systems are the 4-dimensional quaternions, 8-dimensional octonions, and 16-dimensional sedenions, as summarized in the table below along with the real and complex number systems.

Name	Dimension	Symbol
real numbers	1 = 20	$\mathbb {R}$
complex numbers	2 = 21	$\mathbb {C}$
quaternions	4 = 22	$\mathbb {H}$
octonions	8 = 23	$\mathbb {O}$
sedenions	16 = 24	$\mathbb {S}$
2n-ions	2n

According to a 2002 paper by American mathematician Robert P. C. de Marrais, after the sedenions are the 32-dimensional pathions, the 64-dimensional chingons, the 128-dimensional routons, the 256-dimensional voudons (coined by Tony Smith), and ad infinitum. Except for the term voudon, these terms were all coined by de Marrais. They are summarized in the table below.

Name	Dimension	Symbol	Etymology	Other names
pathions	32 = 25	$\mathbb {P}$	32 paths of wisdom of Kabbalah, from the Sefer Yetzirah	trigintaduonions ($\mathbb {T}$), 32-ions
chingons	64 = 26	$\mathbb {X}$	64 hexagrams of the I Ching	sexagintaquattuornions, 64-ions
routons	128 = 27	$\mathbb {U}$	Massachusetts Route 128, of the "Massachusetts Miracle"	centumduodetrigintanions, 128-ions
voudons	256 = 28	$\mathbb {V}$	256 deities of the Ifá pantheon of Voodoo or West African Vodún	ducentiquinquagintasexions, 256-ions

Category theory

Category theory is the study of categories, which are collections of objects and morphisms (or arrows), from one object to another. It generalizes many common notions in Algebra, such as different kinds of products, the notion of kernel, etc. See Category Theory for additional information.

Definitions & Notations

Definition 1: A (locally small) category ${\mathcal {C}}$ consists of

A collection $\mathrm {Obj} ({\mathcal {C}})$ of objects.

A collection $\mathrm {Arr} ({\mathcal {C}})$ of morphisms.

For any $X,Y\in \mathrm {Obj} ({\mathcal {C}})$, $\mathrm {Hom} (X,Y)$ is the subcollection of $\mathrm {Arr} ({\mathcal {C}})$ of morphisms from $X$ to $Y$, where each $\mathrm {Hom} (X,Y)$ is required to be a set (hence the term locally small).

These obey the following axioms:

There is a notion of composition. If $X,Y,Z\in \mathrm {Obj} ({\mathcal {C}})$, $f\in \mathrm {Hom} (X,Y)$ and $g\in \mathrm {Hom} (Y,Z)$, then $f$ and $g$ are called a composable pair. Their composition is a morphism $g\circ f\in \mathrm {Hom} (X,Z)$.

Composition is associative. $f\circ (g\circ h)=(f\circ g)\circ h$ whenever the composition is defined.

For any object $X$, there is an identity morphism $\mathrm {id} _{X}\in \mathrm {Hom} (X,X)$ such that if $Y,Z$ are objects, $f\in \mathrm {Hom} (Y,X)$ and $g\in \mathrm {Hom} (X,Z)$, then $\mathrm {id} _{X}\circ f=f$ and $g\circ \mathrm {id} _{X}=g$.

Note that we demand neither $\mathrm {Obj} ({\mathcal {C}})$ nor $\mathrm {Arr} ({\mathcal {C}})$ to be sets; if they are both in fact sets, then we call our category small.

Definition 2: A morphism $f$ has associated with it two functions $\mathrm {dom}$ and $\mathrm {cod}$ called domain and codomain respectively, such that $f\in \mathrm {Hom} (X,Y)$ if and only if $\mathrm {dom} \,f=X$ and $\mathrm {cod} \,f=Y$. Thus two morphisms $f,g$ are composable if and only if $\mathrm {cod} \,f=\mathrm {dom} \,g$.

Remark 3: Unless confusion is possible, we will usually not specify which Hom-set a given morphism belongs to. Also, unless several categories are in play, we will usually not write $X\in \mathrm {Obj} ({\mathcal {C}})$, but just "$X$ is an object". We may write $X{\stackrel {f}{\longrightarrow }}Y$ or $f:X\to Y$ to implicitly indicate the Hom-set $f$ belongs to. We may also omit the composition symbol, writing simply $gf$ for $g\circ f$.

Basic Properties

Lemma 4: Let $X$ be an object of a category. The identity morphism for $X$ is unique.

Proof: Assume $i$ and $j$ are identity morphisms for $X$. Then $i=i\circ j=j$.

Example 5: We present some of the simplest categories:

i) $0$ is the empty category, with no objects and no morphisms.

ii) $1$ is the category containging only a single object and its identity morphism. This is the trivial category.

iii) $2$ is the category with two objects, $X$ and $Y$, their identity morphisms, and a single morphism $f\in \mathrm {Hom} (X,Y)$.

iv) We can also have a category like $2$, but where we have two morphisms $f,g\in \mathrm {Hom} (X,Y)$ with $f\neq g$. Then $f$ and $g$ are called parallel morphisms.

v) $3$ is the category with three objects $X,Y,Z$. We have $f\in \mathrm {Hom} (X,Y)$, $g\in \mathrm {Hom} (Y,Z)$ and $h=gf\in \mathrm {Hom} (X,Z)$.

Initial and Final Objects

Definition An object $I$ in a category is called initial or cofinal, if for any object $X$ there exists a unique morphism $f:I\to X$

Lemma If $I$ and $J$ are initial objects, then they are isomorphic.

Proof: Let $i:I\to J$ and $j:J\to I$ be the unique morphisms between $I$ and $J$. Given that both $I$ and $J$ have a unique endomorphism because of their initiality, this morphism must be the identity. Therefore $i\circ j$ and $j\circ i$ are the respective identity morphisms, making $I$ and $J$ isomorphic.

Definition An object $F$ in a category is called final or coinitial, if for any object $X$ there exists a unique morphism $f:X\to F$

Lemma If $T$ and $S$ are final objects, then they are isomorphic.

Proof Pass to isomorphicness of initial objects in the cocategory.

Some examples of categories

• $\mathbf {Set}$: the category whose objects are sets and whose morphisms are maps between sets.
• $\mathbf {FinSet}$: the category whose objects are finite sets and whose morphisms are maps between finite sets.
• The category whose objects are open subsets of $\mathbb {\mathbb {R} } ^{n}$ and whose morphisms are continuous (differentiable, smooth) maps between them.
• The category whose objects are smooth (differentiable, topological) manifolds and whose morphisms are smooth (differentiable, continuous) maps.
• Let $k$ be a field. Then we can define $k-\mathbf {Vect}$: the category whose objects are vector spaces over $k$ and whose morphisms are linear maps between vector spaces over $k$.
• $\mathbf {Group}$: the category whose objects are groups and whose morphisms are homomorphisms between groups.

In all the examples given thus far, the objects have been sets with the morphisms given by set maps between them. This is not always the case. There are some categories where this is not possible, and others where the category doesn't naturally appear in this way. For example:

• Let ${\mathcal {G}}$ be any category. Then its opposite category ${\mathcal {G}}^{op}$ is a category with the same objects, and all the arrows reversed. More formally, a morphism in ${\mathcal {G}}^{op}$ from an object $X$ to $Y$ is a morphism from $Y$ to $X$ in ${\mathcal {G}}$.
• Let $M$ be any monoid. Then we can define a category with a single object, with morphisms from that object to itself given by elements of $M$ with composition given by multiplication in $M$.
• Let $G$ be any group. Then we can define a category with a single object, with morphisms from that object to itself given by elements of $G$ with composition given by multiplication in $G$.
• Let ${\mathcal {C}}$ be any small category, and let ${\mathcal {D}}$ be any category. Then we can define a category ${\mathcal {D}}^{\mathcal {C}}$ whose objects are functors from ${\mathcal {C}}$ to ${\mathcal {D}}$ and whose morphisms are natural transformations between the functors from ${\mathcal {C}}$ to ${\mathcal {D}}$.
• $\mathbf {Cat}$: the category whose objects are small categories and whose morphisms are functors between small categories.

Lattice theory

A lattice is a poset such that each pair of elements has a unique least upper bound and a unique greatest lower bound.

Matroids

A matroid is an algebraic construct that is related to the notion of independence.

Matroids are an abstraction of several combinatorial objects, among them graphs and matrices. The word matroid was coined by Whitney in 1935 in his landmark paper "On the abstract properties of linear dependence". In defining a matroid Whitney tried to capture the fundamental properties of dependence that are common to graphs and matrices. Almost simultaneously, Birkhoff showed that a matroid can be interpreted as a geometric lattice. Maclane showed that matroids have a geometric representation in terms of points, lines, planes, dimension 3 spaces etc. Often the term combinatorial geometry is used instead of simple matroids. However, combinatorial geometry has another meaning in mathematical literature. Rank 3 combinatorial geometries are frequently called linear spaces. Matroids are a unifying concept in which some problems in graph theory, design theory, coding theory, and combinatorial optimization become simpler to understand.

Authors

Authors:

• A. Mani
• Jaden Mathos
• Richard Campanha
• The Scarlet Letter
• Mathmensch
• Rgdboer

Manual of Style

This section defines the style rules that should be applied throughout the Abstract Algebra wikibook.

Purpose

This is intended as a University-level textbook for students of mathematics. Readers are therefore expected to be familiar with math fundamentals, and with the material in the Algebra and Linear Algebra wikibooks.

Language

The style of the language should be that of an ordinary math textbook: clear and precise but without talking down to the reader. Personal comments should be avoided.

The book should use standard American English spelling throughout.

Structure

Each page should read like a section of a paper textbook, with external links to further reading where appropriate.(?)

Chapter and section titles

For top-level chapter titles, all words should be capitalised apart from articles and prepositions (e.g. "Equivalence Relations and Congruence Classes"). Sub-headings within a page should only have the first letter of the heading capitalised.

Page length restrictions

There are no additional page length restrictions imposed by this style guide, but do follow the global Wikibooks convention of limiting page lengths at 35k (?)

Templates

With the exception of unimportant comments, each paragraph of text should be preceded with a "type declaration". Common types are Definition, Theorem, Lemma, Example, Note and Remark. A proof should be preceded with the word "Proof" in italics and a semicolon, and ended with a black square: ∎ . Code:

{{Unicode|∎}}

The same counter should be used for all types of paragraphs. Example:

Definition 1: ...

Theorem 2: ...

Proof: ... ∎

Remark 3: ...

etc...

Links

Don't link outside the book (except in the introduction to the book as a whole, which can link to other books that are prerequisites).

Navigation

There are no navigation templates.

Images

All images should be in Wikimedia commons. Since the vast majority of images will be diagrams to illustrate a point in the surrounding text, thumbnails will probably not be appropriate.

Categories

All book chapters belong under the single category Book:Abstract Algebra

Notation

Left = first usage, right = last usage

• Groups: $G$
• Elements of groups: $\sigma ,\tau ,\rho$
• Subgroups: $H,K,I$
• Elements of subgroups: $\eta ,\kappa ,\iota$
• Normal subgroups: $N,M$
• Normal series: $N_{1},\ldots ,N_{n}$, $M_{1},\ldots ,M_{k}$
• Generic integers: $n,k,m,l,j$
• Summation indices: $j,k,n$
• Sequence indices: $l,m$

The hierarchy of rings

Commutative rings

Definition 11.1:

A ring $R$ with multiplication $\cdot$ is called commutative if and only if $a\cdot b=b\cdot a$ for all $a,b\in R$.

Examples 11.2:

• The whole numbers $\mathbb {Z}$ are commutative.
• The matrix ring $\mathbb {R} ^{n\times n}$ of $n$-by-$n$ real matrices with matrix multiplication and component-wise addition is not commutative for $n\geq 2$.

In commutative rings, a left ideal is a right ideal and thus a two-sided ideal, and a right ideal also.

Integral domains

Definition 11.3:

An integral domain is defined to be a commutative ring (that is, we assume commutativity by definition) such that whenever $ab=0$ ($a,b\in R$), then $a=0$ or $b=0$.

We can characterize integral domains in another way, and this involves the so-called zero-divisors.

Definition 11.4:

Let $R$

Thus, a ring is an integral domain iff it has no zero divisors.

Unique factorisation domains

Theorem 11.?:

Suppose that $R$ is a commutative ring

Principal ideal domains

Due to its importance in algebra, we'll briefly give the definition of noetherian rings, which is a fairly exhaustive class of rings for which many useful properties hold. The theory of noetherian rings is well-studied, powerful and extensive, and we'll only study it in detail in the wikibook on Commutative Algebra. The reason that we give the definition here is that principal ideal domains are noetherian rings, which will imply that they are, in fact, unique factorisation domains.

Definition 11.?:

Let $R$ be a commutative ring. $R$ is called noetherian iff for every sequence of ideals $(I_{n})_{n\in \mathbb {N} }$ of $R$ such that

$I_{1}\subseteq I_{2}\subseteq I_{3}\subseteq \cdots \subseteq I_{k}\subseteq \cdots$

there exists an $N\in \mathbb {N}$ such that $I_{N}=I_{N+1}=I_{N+2}=\cdots$.

This condition can be interpreted to state that every ascending chain of ideals stabilizes. Noetherian rings are named in honour of Emmy Noether.

Theorem 11.?:

Every PID is Noetherian.

Proof:

We observed earlier that the set of all ideals of a ring is inductive, with an explicit description of. If therefore we are given an ascending chain of ideals

Theorem 11.?:

Every PID is a UFD.

Proof:

Let $R$ be a PID, and let $a\in R$.

Euclidean domains

Example 11.? (Gaussian integers):

We have already seen that $\mathbb {Z}$ is a Euclidean domain. Now consider the ring

$\mathbb {Z} [i]:=\{a+ib|a,b\in \mathbb {Z} \}\subseteq \mathbb {C}$

with addition and multiplication induced by that of $\mathbb {C}$. We'll see in the exercises that this is indeed a commutative ring with identity. Furthermore, on it we define a Euclidean function as thus:

$N(a+ib):=a^{2}+b^{2}$

This is indeed a Euclidean function, the units of $\mathbb {Z} [i]$ are $\{+1,-1,+i,-i\}$ and furthermore we may precisely describe the prime elements of $\mathbb {Z} [i]$ and set them in relation to the prime elements of $\mathbb {Z}$:

1. If $p\in \mathbb {Z}$ is a prime in $\mathbb {Z}$, then either it is already a prime in $\mathbb {Z} [i]$, or there is a prime $\pi \in \mathbb {Z} [i]$ in the Gaussian primes such that $p=\pi {\overline {\pi }}$.
2. If $\pi \in \mathbb {Z} [i]$ is a Gaussian prime, then set $n:=\pi {\overline {\pi }}$. Either we have that $n$ is a prime in $\mathbb {Z}$, or $n=p^{2}$, where $p$ is a prime in $\mathbb {Z}$.
3. In 1., if $p\neq 2$, the former case happens if and only if $p\equiv 1\mod 4$ and the latter if and only if $p\equiv 3\mod 4$.

Proof:

First, the proof of multiplicativity of $N$ is relegated to the exercises, that is, you'll show in the exercises that

$N((a+ib)(c+id))=N(a+ib)N(c+id)$.

Then we have to prove that division with remainder holds. Let thus $\sigma :=a+ib$ and $\tau :=c+id$ be elements of $\mathbb {Z} [i]$.

Due to $1=(-1)^{2}=i^{4}=(-i)^{4}$, $1,-1,i,-i$ are units. Any other unit would have to have the form $a+ib$, where $|a|+|b|\geq 2$. Let $c+id$ be its inverse. Then $1=N((a+ib)(c+id))=N(a+ib)N(c+id)=(a^{2}+b^{2})(c^{2}+d^{2})\geq 2$, a contradiction.

Finally, let's prove the statements about the relation of the Gaussian primes to the integer primes.

1. Since $\mathbb {Z} [i]$ is a Euclidean domain, we have a decomposition of $p$ into prime elements of $\mathbb {Z} [i]$, say $p=u\pi _{1}\cdots \pi _{n}$, where $u\in \{+1,-1,+i,-i\}$ is a unit in $\mathbb {Z} [i]$. If $n=1$, we are done. If $n\geq 2$, observe that $p^{2}=N(p)=N(\pi _{1})\cdots N(\pi _{n})$, and since $p$ is prime, uniqueness of prime factorisation in the integers implies that at most two of $N(\pi _{1}),\ldots ,N(\pi _{n})$ are not one and those that are are either $p$ or $p^{2}$. If one is $p^{2}$, there is exactly one prime factor of $p^{2}$ in $\mathbb {Z} [i]$, which is absurd since $p^{2}$ is obviously not irreducible. If ${\displaystyle }$,

Exercises

1. Prove that the Gaussian integers as defined above do form a commutative ring with identity. Use your knowledge on complex numbers (cf. the corresponding chapter in the wikibook on complex analysis).

Rings, ideals, ring homomorphisms

Basic definitions

Definition 10.1:

A ring is a set $R$ together with two binary operations $+:R\times R\to R$ and $\cdot :R\times R\to R$ and two special elements, the unit $1$ and the zero $0$, such that:

1. $R$ is an abelian group with respect to $+$ with neutral element $0$.
2. $R$ is a monoid (that is, a group without inversion) with respect to $\cdot$ with neutral element $1$.
3. The distributive laws hold: $a\cdot (b+c)=a\cdot b+a\cdot c$, $(b+c)\cdot a=b\cdot a+c\cdot a$.

Examples 10.2:

• The whole numbers $\mathbb {Z}$ with respect to usual addition and multiplication are a ring.
• Every field is a ring.
• If $R$ is a ring, then all polynomials over $R$ form a ring. This example will be explained later in the section on polynomial rings.

Definition 10.3:

Let $R$ be a ring. A left ideal of $R$ is a subset $I\subseteq R$ such that the following two things hold:

1. $(I,+)$ is a subgroup of $(R,+)$.
2. $\forall r\in R:rI\subseteq I$, where $rI=\{ri|i\in I\}$ (closedness by left multiplication).

Replacing closedness by left multiplication by closedness by right multiplication, we can define right ideals, and then both-sided ideals. If $I\subseteq R$ is a both-sided ideal of $R$, we write $I\leq R$.

We'll now show an important property of the set of all ideals of a given ring, namely that it's inductive. This means:

Definition 10.4:

Let $(S,\leq )$ be a partially ordered set (that is, the usual conditions transitivity, reflexivity and anti-symmetry are satisfied). $S$ is called inductive if and only if every ascending chain of elements of $S$ (that is, a sequence $(s_{n})_{n\in \mathbb {N} }$ in $S$ such that $s_{1}\leq s_{2}\leq s_{3}\leq \cdots \leq s_{k}\leq \cdots$) has an upper bound (that is, an element $b\in S$ such that $\forall n\in \mathbb {N} :b\geq s_{n}$).

With this definition, we observe:

Theorem 10.5:

If a commutative ring $R$ is given, the set of all ideals $I$ of $R$, partially ordered by inclusion (i.e. $S=\{I\subset R|I\leq R\}\subset 2^{R}$, where we use the convention of Donald Knuth and denote the power set of a set $T$ by $2^{T}$) is inductive.

Proof:

If

$I_{1}\subseteq I_{2}\subseteq I_{3}\subseteq \cdots \subseteq I_{k}\subseteq \cdots$

is an ascending chain of ideals, we set

$J:=\bigcup _{n\in \mathbb {N} }I_{n}$

and claim that $J\leq R$. Indeed, if $a,b\in J$, find $m,n\in \mathbb {N}$ such that $a\in I_{n}$ and $b\in I_{m}$. Then set $N:=\max\{m,n\}$, so that $a,b,a+b\in I_{N}\subseteq J$ since $I_{N}\leq R$. Similarly, if $a\in J$ and $r\in R$, pick $n\in \mathbb {N}$ such that $a\in I_{n}$, whence $ra\in I_{n}\subseteq J$ since $I_{n}\leq R$.$\Box$

Residue class rings

Definition and theorem 10.4:

Let $R$ be a ring, and $I\leq R$. Then we define a relation $\sim _{I}$ on $R$ as follows:

$a\sim _{I}b:\Leftrightarrow a-b\in I$.

This relation is an equivalence relation, and an equivalence class $[a]$ shall be denoted by $a+I$ for $a\in R$. If we define an addition

$(a+I)+(b+I):=(a+b)+I$

and a multiplication

$(a+I)\cdot (b+I):=a\cdot b+I$,

then these two are well-defined (i. e. independent of the choice of the representatives $a$ and $b$) and turn $R/I$ into a ring, called the residue class ring with respect to the ideal $I$.

Proof:

First, we check that $\sim _{I}$ is an equivalence relation.

1. Reflexiveness: $a-a=0\in I$ since $I$ is an additive subgroup.
2. Symmetry: $a-b\in I\Leftrightarrow -(a-b)\in I$ since inverses are in the subgroup.
3. Transitivity: Let $a-b\in I$ and $b-c\in I$. Then $a-c=a-b+(b-c)\in I$, since a subgroup is closed under the group operation.

Then we check that addition and multiplication are well-defined. Let $a+I=a'+I$ and $b+I=b'+I$. Then

$a+b-(a'+b')=a+b-(a+i+b+j)=-i-j\in I$ for certain $i,j\in I$.

Furthermore,

$a\cdot b-a'\cdot b'=a\cdot b-a\cdot b-a\cdot j-i\cdot b-i\cdot b$

for these same $i,j\in I$; this is in $I$ by closedness by left and right multiplication.

The ring axioms directly carry over from the old ring $R$.$\Box$

Ring homomorphisms

Definition 10.5:

Let $R,S$ be rings. A ring homomorphism between the two is a map

$\varphi :R\to S$

such that:

1. For all $a,b\in R$ $\varphi (a+b)=\varphi (a)+\varphi (b)$ and $\varphi (a\cdot b)=\varphi (a)\cdot \varphi (b)$.
2. $\varphi (1_{R})=1_{S}$ ($1_{R}$ is the unit of $R$ and $1_{S}$ of $S$).

Sources

• M. Artin, Algebra (2nd edition)