Calculus/Hyperbolic angle

The usual approach to hyperbolic angle is to call it the argument of a hyperbolic function, like hyperbolic sine (sinh), hyperbolic cosine (cosh), or hyperbolic tangent (tanh). Then the question of hyperbolic angle is obviated by the use of the exponential function

$e^{x}\ =\ \exp(x)\ =\ \sum _{0}^{\infty }x^{n}/n!,$

and $\cosh x={\frac {1}{2}}(e^{x}+e^{-x}),\quad \sinh x={\frac {1}{2}}(e^{x}-e^{-x}),\quad \tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}.$

A more satisfying description of hyperbolic angle follows from analogy with circular angle, the so-called "ordinary angle" which comes with 360 degrees to a circle, or 2π radians. Both angles can be developed as area bounded by radial lines going to the circle or hyperbola.

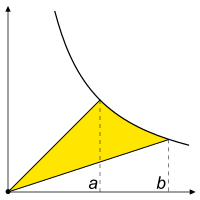
Consider first a circle of radius √2, then the area of the circle is 2π, so that for any sector of the circle, its area equals the radians between the demarcating radii. Similarly, the hyperbola xy = 1 bounds hyperbolic sectors, and the area of a sector is the magnitude of the hyperbolic angle.

Unit area when p = e as exploited by Euler.

Rotation of a circle leaves the size of a circular angle invariant and hyperbolic angle has a similar invariance. Consider the linear transformations that take a square to a rectangle of the same area. These transformations are written as a matrix with reciprocals on the diagonal. Since the hyperbolas xy = constant are preserved, such a transformation is a "hyperbolic rotation" or a "squeeze mapping" (considering the square-to-rectangle-of-the-same-area property).

The analogy breaks down when the potential size of a hyperbolic angle is considered. While circular angle is bounded, the hyperbolic angle is not. One should recall the harmonic series, where the terms become small but the sum is unbounded. The area between a hyperbola and its asymptote is unbounded, so too is hyperbolic angle.

The obscurity of hyperbolic angle flows from its origin. The quantity is essentially the quadrature of a hyperbola, something not accomplished until 1647 by Gregoire de Saint-Vincent. The challenge had stood for two millennia since Aristotle had written his Quadrature of the Parabola. The quadrature of the hyperbola was essentially a leap of faith that a function could be defined by its properties rather than an algebraic expression. The property identified was preservation of area under squeezing. Then for a number p > 1, the area under the hyperbola was called the "hyperbolic logarithm of p", later just the "natural logarithm". Generally, the area is viewed between x = 1 and x = p, but it is clearly equal to a hyperbolic sector between (1,1) and (p, 1/p): Just add the triangle {(0,0), (1,0), (1,1)}, and subtract the triangle {(0,0), (p,0), (p, 1/p)} (They both have area one-half).

Leonard Euler slickly developed the topic by first looking for a unit area: When p = 2.71828... the dented trapezoid or hyperbolic sector has exactly one unit of area. The number is now abbreviated as e. A matrix with e and 1/e on the diagonal transforms the unit sector to another between (e, 1/e) and (e², e⁻²) which is thinner and longer (but still one unit). Euler's approach uses this number as a base for exponentiation, similar to 10ⁿ or 2ⁿ. The standard treatment in precalculus courses uses the inverse of the exponential function to define natural logarithm. In this way the quadrature is avoided and hyperbolic angle obviated.

Rapidity

The various t axes represent time for observers in motion, the corresponding x axes are their lines of simultaneity

The naive approach to velocity does not have an upper bound, but the universe is characterized by the speed of light c: a foot in a nanosecond, an astronomic unit in 500 seconds, or a "light year" in a year. This speed is a high ratio of distance to time, but a finite one. All the speeds v of physics lie in the range [−c, c], so the ratio v/c is in [−1, 1]. This interval is the range of the hyperbolic tangent function; modern kinematics uses tanh(φ) = v/c with φ representing rapidity instead of velocity. Whereas the raw velocity is limited by c, the rapidity is a hyperbolic angle and is unbounded. In special relativity a change of velocity is accomplished by a hyperbolic rotation. Due to the preservation of area by this transformation, the rapidities of different frames of reference are preserved. In physics textbooks this transformation is called a Lorentz transformation or boost of a frame of reference.

Given two rapidities –∞ < x,y < ∞ , the angle sum formula for hyperbolic tangent expresses the velocity that results from the sum of their rapidities:

$\tanh(x+y)={\frac {\tanh x+\tanh y}{1+\tanh x\tanh y}}.$

Assume that v = tanh x and w = tanh y (using velocities expressed as a fraction of light-speed), the formula for the sum of velocities in relativity is

${\frac {v+w}{1+vw}}.$

The dotted line in the diagram is a light-track in spacetime. The green hyperbola is one temporal moment into the future from the origin, depending on velocity. The blue line represents a zero rapidity in (−∞, + ∞), which is arbitrary in light of the hyperbolic rotations. Thus there is an inherent principle of relativity in modeling velocity with rapidity.

Split-complex theory

The complex numbers C of the previous chapter extend R by a square root of minus one, i, a root of X² + 1. Another complex plane D extends R with j, a root of X² − 1. But this binomial equals (X + 1)(X – 1) so it is "already split", as opposed to the first binomial which is "split" by the factoring (X + i)(X − i). Therefore C is called a splitting field, and D is called "split-complex numbers" since its binomial is already split in R.

Elements of D are written $z=t+xj$ with the rule j² = +1. Note that jz then equals x + t j, so the action of j on D is to reflect the plane in the line x = t. The conjugate of z is ${\bar {z}}=t-xj.$

Refer to the series for e^x above and note that when the argument jx is inserted, the odd terms contain a j factor while j disappears in the even terms:

$\exp(jx)=\cosh x+j\sinh x.$

Thus exp maps the j-axis in D to a hyperbolic branch. Furthermore, $\exp(j(a+b))=\exp(ja)\exp(jb),$ so exp is a group homomorphism of the additive group on R into a multiplicative group on the hyperbola branch. In fact, the action of exp(jx) on the hyperbola branch corresponds to the hyperbolic rotation mentioned above.

The lines from 0 to w and z in D are hyperbolic orthogonal when  $z{\bar {w}}+w{\bar {z}}=0.$

The split-complex plane D is used to represent a world with one space dimension and one time dimension, where the units correspond to the speed of light, so that the diagonal lines x = t and x = − t represent the locus of light rays through the origin. Conventionally time is drawn vertically, corresponding to the t-axis here. Then the hyperbola branch exp(ja) through (1,0) represents events in the future of 0, each corresponding to a rapidity a.

The notion of simultaneous events in this world is expressed with hyperbolic orthogonality: if |t| > |x|, then z is a temporal event with respect to 0, and any w hyperbolic orthogonal to z is a space event simultaneous with 0.

For a real number s, the transformation by $z\mapsto e^{sj}z$ is called a boost of D by rapidity s.

Exercises

1) For a in R, find the conjugate of   j e^{a j}.

2) Show that e^{a j} is hyperbolic orthogonal to   j e^{a j}.

3) Draw a diagram with origin 0 and axes through 1 and j. The points in this diagram correspond to events in a world with time but only one space axis. Illustrate a rapidity, and a line of events simultaneous with 0 corresponding to the rapidity, by using the split-complex numbers in the previous exercise.

4) If a and b are two rapidities, show that any boost maps the events $e^{aj}\ {\text{and}}\ e^{bj}$ to events, the difference of whose rapidities is b – a.

5) If two lines are hyperbolic-orthogonal, show that the two images under a boost are also hyperbolic-orthogonal. (Hint: see exercise 3 in the previous chapter)