Trigonometry/Angles of Elevation and Depression

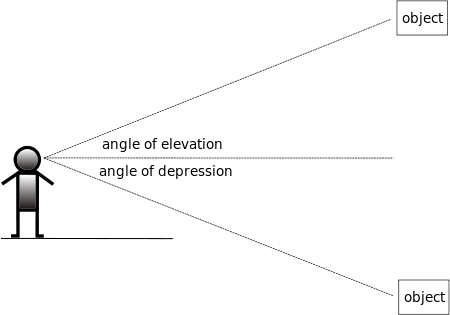
Suppose you are an observer at $O$ and there is an object $Q$ , not in the same horizontal plane. Let $OP$ be a horizontal line such that $O,P,Q$ are in a vertical plane. Then if $Q$ is above $0$ , the angle $\angle QOP$ is the angle of elevation of $Q$ observed from $P$ , and if $Q$ is below $O$, the angle $\angle QOP$ is the angle of depression.

Often when using angle of elevation and depression we ignore the height of the person, and measure the angle from some convenient 'ground level'.

Exercise 1: Opposite, Hypotenuse, Adjacent Look at the diagram above. $\angle MLT$ is a right angle. What would you give as the translation of the labels into English?

Example 1: A Flagpole From a point $10m$ from the base of a flag pole, its top has an angle of elevation of $50^{\circ }$ . Find the height of the pole. [diagram] If the height is $h$ , then ${\frac {h}{10}}=\tan(50^{\circ })$ . Thus $h=10\tan(50^{\circ })=11.92m$ (to two decimal places).

Example 2: A $15m$ High Flagpole A flag pole is known to be $15m$ high. From what distance will its top have an angle of elevation of $50^{\circ }$ ? [diagram] If the distance is $d$ , then ${\frac {15}{d}}=\tan(50^{\circ })$ . Thus $d={\frac {15}{\tan(50^{\circ })}}=12.59m$ (to two decimal places).

Example 3: A $20m$ Tower From the foot of a tower $20m$ high, the top of a flagpole has an angle of elevation of $30^{\circ }$ . From the top of the tower, it has an angle of depression of $25^{\circ }$ . Find the height of the flagpole and its distance from the tower. Let the height of the flagpole be h and its distance be d. Then (i) ${\frac {h}{d}}=\tan(30^{\circ })$ The top of the flagpole is below the top of the tower, since it has an angle of depression as viewed from the top of the tower. It must be $20-h$ metres lower, so (ii) ${\frac {20-h}{d}}=\tan(25^{\circ })$ Adding these two equations, we find (iii) ${\frac {20}{d}}=\tan(30^{\circ })+\tan(25^{\circ })$ From this (how?) we find $d=19.16m\ ,\ h=11.06m$ (both to two decimal places).

Example 4: Yet another Flagpole From a certain spot, the top of a flagpole has an angle of elevation of $30^{\circ }$ . Move $10m$ in a straight line towards the flagpole. Now the top has an angle of elevation of $50^{\circ }$ . Find the height of the flagpole and its distance from the second point. [diagram] Let the height be $h$ and its distance from the second point be $x$ . Then $\cot(50^{\circ })={\frac {x}{h}}\ ;\ \cot(30^{\circ })={\frac {x+10}{h}}$ Subtracting the first expression from the second, $\cot(30^{\circ })-\cot(50^{\circ })={\frac {10}{h}}$ $h={\frac {10}{\cot(30^{\circ })-\cot(50^{\circ })}}=11.20m$ $x=h\cot(50^{\circ })=9.40m$