Statistical Thermodynamics and Rate Theories/Printable version

Statistical Thermodynamics and Rate Theories

The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/Statistical_Thermodynamics_and_Rate_Theories

Permission is granted to copy, distribute, and/or modify this document under the terms of the Creative Commons Attribution-ShareAlike 3.0 License.

Molecular Energy Levels

To predict the properties of gases from their molecular properties, we must first know the different states the molecule can occupy and their energy levels.

Degrees of freedom

Molecular degrees of freedom refer to the number of ways a molecule in the gas phase may move, rotate, or vibrate in space. Three types of degrees of freedom exist, those being translational, rotational, and vibrational. The number of degrees of freedom of each type possessed by a molecule depends on both the number of atoms in the molecule and the geometry of the molecule, with geometry referring to the way in which the atoms are arranged in space. The number of degrees of freedom a molecule possesses plays a role in estimating the values of various thermodynamic variables using the equipartition theorem. These molecular degrees of freedom essentially describe how a molecule is able to contain and distribute its energy.

Degree of freedom	Monatomic	Linear molecules	Non-linear molecules
Translational	3	3	3
Rotational	0	2	3
Vibrational	0	3N - 5	3N - 6
Total	3	3N	3N

Translational degrees of freedom

Translational degrees of freedom arise from a gas molecule's ability to move freely in space. A molecule may move in the x, y, and z directions of a Cartesian coordinate system, appearing at a new position in space (relative to a starting position) via translation. A gas molecule is not restricted in which direction it may move, thus it has three translational degrees of freedom. This holds true for all gas molecules, whether they are monatomic, diatomic, or polyatomic, as any molecule may move freely in all directions in three-dimensional space.

Rotational degrees of freedom

A molecule's rotational degrees of freedom represent the number of unique ways the molecule may rotate in space about its center of mass which a change in the molecule's orientation. These axes may pass through atoms or bonds. By examining the molecule's symmetry (and, by extension, its geometry), the number of rotational degrees of freedom can quickly and easily be determined. A monatomic gaseous molecule such as a noble gas possesses no rotational degrees of freedom, as the center of mass sits directly on the atom and no rotation which creates change is possible.

A diatomic molecule, like H₂ or HCl, has two rotational degrees of freedom. The center of mass of a linear molecule rests somewhere between the two terminal atoms. In the case of HCl it exists somewhere along the bond. The center of mass can be taken as the origin of a three-dimensional Cartesian grid, the z axis of which runs along the bond and through the two atoms. Rotation about the x and y axes generates a noticeable change in the molecule's orientation, while rotation about the z axis (analogous to the monatomic case) produces no change in the molecule and is considered a 'lost' rotational degree of freedom.

A polyatomic molecule may have either two or three rotational degrees of freedom, depending on the geometry of the molecule. For a linear polyatomic, such as CO₂ or C₂H₂, the molecule has only two rotational degrees of freedom. The reason for this is discussed in the previous paragraph.

Vibrational degrees of freedom

The number of vibrational degrees of freedom (or vibrational modes) of a molecule is determined by examining the number of unique ways the atoms within the molecule may move relative to one another, such as in bond stretches or bends. This can be determined mathematically using the $3N-6=n_{DOF}$ rule, where $N$ is the number of atoms in the molecule and $n_{DOF}$ is the number of vibrational degrees of freedom. Note that for linear molecules, the rule instead becomes $3N-5=n_{DOF}$, meaning a linear polyatomic made up of $N$ atoms will have one more vibrational degree of freedom than a non-linear polyatomic with $N$ atoms. Application of the rule for linear molecules shows that a diatomic molecule has only one vibrational degree of freedom. This is a logical conclusion, as there is only one bond vibration possible, a stretch of the bond between the two atoms.

• The three normal vibrational modes of water: bending (left), symmetric stretch (centre), and asymmetric stretch (right).
• 
• 
• 

As an example, water, a non-linear triatomic, should have three vibrational degrees of freedom, since $3(3)-6=3$. The three vibrational modes corresponding to these three vibrational degrees of freedom can be seen above. These vibrational modes were determined computationally.

Translational energy

A gas particle can move through space in three independent directions: x, y, and z. Each of these directions is a distinct translational degree of freedom. For ideal gases, these particles can move freely through space in any of these directions until it collides with the wall of its container. For isolated systems, collisions with the wall of the container are assumed to be elastic, meaning no energy is lost upon impact.

Particle in a 1D Box

The first quantum mechanical model used for describing translation is a particle in a simple 1D box. It is free to move anywhere along one axis (usually assigned to be the x axis) between the arbitrarily assigned boundary limits 0 and a. At distances smaller than 0 and greater than “a” the potential energy function immediately rises to infinity. The particle cannot move past these points. 0 and a represent the walls of the 1D box. We can mathematically assign boundary conditions using this information which allows the derivation of the wave function for a particle in a 1D box. The resulting piece-wise function, wave function and energy level equation are given as follows,

${\mathcal {V}}(x)={\begin{cases}\infty ,x<0\\0,0{\leq }x{\leq }a\\\infty ,x>a\end{cases}}$

$\Psi (x)={\sqrt {\frac {2}{a}}}\sin {\left({\frac {n\pi x}{a}}\right)}$

$n=1,2,3,...$

As well as the corresponding energy levels of the system.

$\epsilon _{n}={\frac {h^{2}n^{2}}{8ma^{2}}}$

Note: In the equations above m represents the mass of the gas particle, and h is Planck's constant.

Zero-Point Energy

The energy levels for translation within the box are quantized, only discrete energy levels can be occupied by the particle at any given time. Each of these energy levels are defined by a single quantum number n. n can take on any integer values starting from 1 and up to a hypothetical infinity. The n = 0 state for a particle in a box does not exist. The particle, in accordance with the Heisenberg uncertainty principle cannot be motionless. If this were to be the case then both the momentum and position of the particle could be determined simultaneously, which is a violation of the principle. The energy of a particle in a 1D box at the lowest translational energy level is therefore non-zero (i.e., n = 1).

Probability Density Plots and the Correspondence Principle

It is possible to construct a probability density plot of the particle in a 1D box wave function. The plot is characterized by sizable “humps” at low values of n. For example, at n=1 there is one large hump which spans from a minimum at x = 0, a maximum somewhere in the center and a second minimum at x = a. These minimums represent regions of zero probability density. In other words, the particle will not be found in these regions.

As n increases the spacing between humps of the probability density plot becomes smaller and smaller until a near continuum is achieved at sufficiently high values of n. It must also be noted that the magnitude of the energy spacing’s between translational energy levels is extremely small relative to the amount of energy available to a particle under normal conditions. At room temperature ideal gas particles will occupy very high energy levels. As we increase the quantum number to a large enough value the behavior of the system will begin to reproduce that of classical mechanics in that the particle is essentially equally likely to be found anywhere in the box rather than within discrete hump regions seen at lower values of n. This is what is known as the correspondence principle.

Particle in a 3D Box

The correspondence principle applies to a 3D box as well. For a particle in a 3D box, the particle is able to move in any direction along the x, y and z axes. Since its motion now incorporates a combination of three possible directions the system must include two additional quantum numbers to compensate for the difference. n_x, n_y, and n_z for the x, y, and z dimensions, respectively. Both the wave function and the equation for the energy levels must be adjusted to compensate for the new quantum numbers. These are given as follows,

$\Psi _{n_{x},n_{y},n_{z}}={\sqrt {\frac {8}{abc}}}\sin \left({\frac {n_{x}{\pi }x}{a}}\right)\sin \left({\frac {n_{y}{\pi }y}{b}}\right)\sin \left({\frac {n_{z}{\pi }z}{c}}\right)$

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8m}}\left({\frac {{n_{x}}^{2}}{a^{2}}}+{\frac {{n_{y}}^{2}}{b^{2}}}+{\frac {{n_{z}}^{2}}{c^{2}}}\right)$

a, b, and c represent the length of each corresponding side of the box. If the box were a cube then the energy level equation can be simplified because sides a, b, and c of the cube are all equal. The resulting equation would take on the form,

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8m{a^{2}}}}({{n_{x}}^{2}}+{{n_{y}}^{2}}+{{n_{z}}^{2}})$

For a particle in a cube some combinations of quantum numbers will give the same energy level. Energy levels with a different set of quantum numbers but having the same energy are said to be degenerate and unless all three of the quantum numbers are identical there is always another combination of the three quantum numbers that will give rise to a degenerate state.

Example

Calculate the energy difference, $\Delta E$, for the translation of N₂ from the ground state to the first excited state. Assume the box is a cube with an edge length of 10 cm.

Solution

The ground state, where $n_{x}=n_{y}=n_{z}=1$, has a degeneracy of 1. The first excited state has a degeneracy of 3, involving the different combinations of quantum numbers $n=1,1,$ and 2. Can be determined by using the following equation:

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8m}}\left({\frac {{n_{x}}^{2}}{a^{2}}}+{\frac {{n_{y}}^{2}}{b^{2}}}+{\frac {{n_{z}}^{2}}{c^{2}}}\right)$

However because all edges of the cube is 10 cm, then a=b=c=10 cm = 0.1 m. Then the equation becomes:

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8m{a^{2}}}}\left({{n_{x}}^{2}}+{{n_{y}}^{2}}+{{n_{z}}^{2}}\right)$

The mass of N₂ can be determined with the following equation:

$\mu ={\cfrac {m_{N}m_{N}}{m_{N}+m_{N}}},\!\,$

$\mu ={\cfrac {m_{N}^{2}}{2m_{N}}},\!\,$

$\mu ={\cfrac {m_{N}}{2}},\!\,$

$\mu ={\cfrac {14.0067u}{2}},\!\,$

$\mu =(7.00335u)(1.660549\times 10^{-27}kg/u),\!\,$

$\mu =1.16294\times 10^{-26}kg,\!\,$

Using the mass the $\Delta E$ can now be determined.

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8m{a^{2}}}}({{n_{x}}^{2}}+{{n_{y}}^{2}}+{{n_{z}}^{2}})-({{n_{x}}^{2}}+{{n_{y}}^{2}}+{{n_{z}}^{2}})$

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {({6.626\times 10^{-34}})^{2}Js}{8(1.16294\times 10^{-26}kg){0.1m^{2}}}}({{2}^{2}}+{{1}^{2}}+{{1}^{2}})-({{1}^{2}}+{{1}^{2}}+{{1}^{2}})$

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {{4.3904\times 10^{-67}}J^{2}s^{2}}{9.30352\times 10^{-28}kgm^{2}}}(6-3)$

$\epsilon _{n_{x},n_{y},n_{z}}=1.4157\times 10^{-39}J$

Further Reading

Wikipedia entry on particle in a box models

Rotational Energy

Molecules that consist of more than one atom have rotational angular momentum. The rotational motion which is generated by these molecules is purely kinetic as each molecule rotates around the molecules centre of mass. A good approximation which makes interpreting the rotational energy levels easier is the rigid rotor approximation which is mentioned below. Essentially this approximation assumes that the molecule has a fixed bond length and it does not vibrate while it undergoes rotation about its centre of mass. This approximation makes it easy to calculate the bond length by simply knowing the rotational energy spacings of the molecule observed in a spectroscopic experiment.

The rotational kinetic energy of an object depends on its moment of inertia, I,

$I=\Sigma _{i}m_{i}r_{i}^{2}$

where $m_{i}$ is the mass of the atom $i$, $r_{i}$ is the distance of that atom from the centre of mass of the molecule. Any molecule has three perpendicular axes of rotation each of which intersect at the centre of mass for that molecule, the moment of inertia is the rotational motion found at the center of mass of a molecule. Each of these axes of rotation could be distant from one another, or they could all be equal which leads to different types of rigid rotors. A large moment of inertia is basically based on either larger atomic masses and/or longer bonds.

Types of Rigid Rotor

Type	Moments of Inertia	Examples
Linear Rotors	$I_{1}=I_{2}=I_{3}=0$	N2, CO2, C2H2
Spherical Rotors	$I_{1}=I_{2}=I_{3}\neq 0$	CH4, SF6
Symmetric Rotors	$I_{1}=I_{2}\neq I_{3}$	NH3, CH3Cl
Asymmetric Rotors	$I_{1}\neq I_{2}\neq I_{3}$	H2O, H2CO, Most Molecules

Linear Rotors

In this course we are mostly concerned with linear rotors, using these systems simplifies the math. If we are using a linear rigid rotor, the bond length is constant due to the rigid rotor approximation, and the centre of mass is constant, therefore the moment of inertia can be simplifies using the reduced mass as follows:

$I=\Sigma \mu r_{e}^{2}$

here, $\mu$ is the reduced mass of the linear rotor where ${\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$, and $r_{e}$ is the bond length of the diatomic linear rotor. The reduced mass the inertial mass of two atom system following Newtonian Mechanics. This can then be used to solve the Schrödinger equation which is given in example 2 below. By solving this equation we find that there are two quantum numbers which determine the energy levels of a rotating rigid rotor, M and J both of which are described below in example 2.

Zero Point Energy of Linear Rotors

Unlike the particles in a box model, which has a non zero energy minima due to the fact that the lowest energy state corresponds to the n=1 state, the linear rotor can have an energy of zero in the ground state corresponding to a molecule which is not rotating in space. This is the case since $J=0,1,2...$ when $J=0$ the energy of the system is equal to zero. Since the orientation in space is not known for a linear rotor it obeys the Heisenberg uncertainty principle which states that we cannot simultaneously determine the momentum and the position of the particle. Where each energy level can exist using following equation

$E_{J}={\frac {\hbar }{\mu r_{e}^{2}}}\times J(J+1)$

where J is the quantum number, $\mu$ is the reduced mass, r_e² is the length of the bond from the center of mass and ħ is reduced Planck's constant where Planck's constant is divided by 2π. From inserting J=0 in this equation above, we see $\epsilon _{0}=0$.

Degeneracy of Rotational States

The rotational levels of a diatomic only depend on the quantum number J (orbital angular momentum quantum number) and does not have any dependence on the quantum number M. However, as the quantum number J increases, the degeneracy of the states increases since there are more possible values of M, which is the magnetic quantum number which are as follows

$J=0,1,2...$

$M=-J,...,0,...,+J$

Therefore, as the quantum number J increases, the degeneracy of the states also increases. The degeneracy of the states can be calculated using the following equation:

$g_{J}=2J+1$

Degeneracy occurs when there are accessible states present at the same energy level, for example, when J=1, M_J= -1,0,+1 meaning there are 3 different degeneracies at quantum number J=1

Rotational Spectroscopy of Linear Rotors

Linear rotors which contain a permanent dipole are able to be observed through rotational-vibrational spectroscopy. These molecules exhibit fine structure of lines which are all separated by a constant value. This value can be used to determine the bond length of the diatomic in question but using the following equations.

$v=2B(J+1)$ and $B={\frac {h}{8\pi ^{2}cI}}$

where $v$ is the spacing of the rotational lines, $B$ is the rotational constant, $h$ is planks constant which has a value of $6.626\times 10^{-34}Js$, $c$ is the speed of light and $I$ is the moment of inertia. Once we know the value of $B$ we can then use this value to calculate the bond length of the diatomic which is being observed.

Example 1

Calculation of the bond length of HCl from the rotational constant.

Rotational Angular Momentum and the Rigid Rotor Approximation

Rotational energy is purely kinetic, which is a result of angular momentum in the molecule (How quickly the molecule is spinning in space). It can be assumed that the molecule is rigid for an ideal gas, this is because the change in the bond length for a vibration is small in comparison to the total length of the bond, this is called the Rigid Rotor Approximation.

Linear Rotors

The rotation of an object depends on its moment of inertia $I=\Sigma _{i}m_{i}r_{i}^{2}$ where $m_{i}$ is the mass of atom i, and $r_{i}$ is the distance of atom i to the axis of rotation. This expression works well if the diatomic molecule consists of only the same element (e.g. $O_{2},N_{2}$). For diatomic molecules which do not consist of the same elements (e.g. $HCl,NO,NaF$) this expression can be more work intensive then needed. For diatomic molecules which do not comprise of the same elements the expression $I=\mu r_{e}^{2}$ is significantly less work intensive to use in comparison to the previously stated equation. Where $r_{e}^{2}$ is the bond length of the diatomic molecule and $\mu$ is the reduced mass of the molecule, $\mu$ is given by the equation $\mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$ where $m_{1}$ is the atomic mass of atom 1, and $m_{2}$ is the atomic mass of atom 2.

Rotational Spacings

Example of a pure rotational absorption spectrum

The spacings of rotational transitions are constant, and are commonly referred to as a rotational constants ${\bar {B}}$. For linear rotors the spacing is $2{\bar {B}}$ between each rotational transition as can be seen in the image to the right.

Utilizing the equation for the rotational constant ${\bar {v}}=2{\bar {B}}(J+1)$ we can find the value for ${\bar {B}}$ and then use it in the equation ${\bar {B}}={\frac {h}{8\pi ^{2}cI}}$ and solve for the moment of inertia $I$, where $h$ is Planck's constant, and $c$ is the speed of light. Once the moment of inertia is calculated it is simply the matter of solving for the diatomic bond length $r_{e}$ which can be found by $r_{e}={\sqrt {\frac {I}{\mu }}}$.

Sample Problem

Calculate the Bond Length of HCl from the Rotational Constant.

Knowing HCl has a rotational constant value of 10.59341 cm⁻¹, the Planck's constant is 6.626 × 10⁻³⁴J s, and the speed of light being 2.998 × 10¹⁰ cm s⁻¹. We then solve for the moment of inertia such that:

${\bar {B}}={\frac {h}{8\pi ^{2}cI}}$

$I={\frac {h}{8\pi ^{2}c{\bar {B}}}}$

$I={\frac {6.626\times 10^{-34}Js}{8\pi ^{2}(2.998\times 10^{10}cm/s)(10.59341cm^{-1})}}$

$I=2.642401\times 10^{-47}Js^{2}$

$I=2.642401\times 10^{-47}(kgm^{2}/s^{2})s^{2}$

$I=2.642401\times 10^{-47}kgm^{2}$

The next step is to calculate the reduced mass $\mu$. Knowing that the mass of hydrogen is 1.00794 u, and the mass of chlorine is 35.4527 u.

$\mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$

$\mu ={\frac {(1.00794u)\times (35.4527u)}{(1.00794u)+(35.4527u)}}$

$\mu ={\frac {35.73419u^{2}}{36.46064u}}$

$\mu =0.9800758u$

$\mu =0.9800758u\times {\frac {1.6605\times 10^{-27}kg}{1u}}$

$\mu =1.627454\times 10^{-27}kg$

Now knowing all of the variable it is just a matter of solving for the bond length $r_{e}$.

$r_{e}={\sqrt {\frac {I}{\mu }}}$

$r_{e}={\sqrt {\frac {2.642401\times 10^{-47}kgm^{2}}{1.627454\times 10^{-27}kg}}}$

$r_{e}={\sqrt {1.623641\times 10^{-20}m^{2}}}$

$r_{e}=1.274222\times 10^{-10}m$

$r_{e}=1.274222$ Å

$r_{e}=1.274$ Å

Example 2

Calculation of the energy for the transition of N₂ from the ground to first excited rotational state.

Solution

For N₂, the reduced mass is calculated using an atomic mass of 14.0067 u for nitrogen. Since it is a diatomic molecule, the equation can be simplified to the following where $m$ represents the mass of a nitrogen atom:

$\mu ={\frac {m^{2}}{2m}}$

$\mu ={\frac {m}{2}}$

$\mu ={\frac {14.0067u}{2}}$

$\mu =7.0033u$

$\mu =(7.0033u)\left({\frac {1.660539040\times 10^{-27}kg}{u}}\right)$

$\mu =1.1629\times 10^{-26}kg$

For the rigid rotor, the lowest possible energy state is J=0 so the ground state rotational energy is always zero. The rotational energy levels are only dependent on quantum number J and only the ∆𝐽 = ±1 transitions can occur. In the case of the transition from the ground to the first excited state, the following is a diagram that represents the transition.

The energy for the transition J=1 ← J=0 is calculated as follows:

$\Delta \epsilon ={\frac {\hbar ^{2}}{2\mu r_{e}^{2}}}J(J+1)-{\frac {\hbar ^{2}}{2\mu r_{e}^{2}}}J(J+1)$

$\Delta \epsilon ={\frac {\hbar ^{2}}{2\mu r_{e}^{2}}}1(1+1)-{\frac {\hbar ^{2}}{2\mu r_{e}^{2}}}0(0+1)$

$\Delta \epsilon ={\frac {\hbar ^{2}}{\mu r_{e}^{2}}}$

$\Delta \epsilon ={\frac {(1.0545718Js)^{2}}{(1.1629\times 10^{-26}kg)(1.098\times 10^{-10}m)^{2}}}$

$\Delta \epsilon =7.9320\times 10^{-23}J$

Vibrational energy

Molecular vibrations occur when atoms in a molecule are in periodic motion while the molecule as a whole has constant translational and vibrational motion. Vibrational energy is different from translational energy (how a molecule translates through 3-dimensional space along the x,y, and z Cartesian coordinates) and rotational energy (how fast a molecule spins) in that the focus is placed on how a chemical bond behaves with respect to the quantum harmonic oscillator approximation.

Vibrational Energy Levels

Rotational-vibrational spectrum of HCl

The Potential Energy Surface of Molecules

Chemical bonds are formed due to electrostatic interactions between protons and electrons, and can occur as nuclear-electron attractions, electron-electron repulsion, and inter-nuclear repulsion. As a bond forms due to the nuclear electron attractions between a proton and electron, the electron density increases in the space between two nuclei. For a diatomic, the potential energy is only a function of the distance between the two atoms, and the strength of these components changes depending on the distance between the atoms. Bonding is generally stronger when two nuclei are close, but this close proximity also increases internuclear and core-core repulsions. Hence, the potential energy is lowest at the equilibrium bond length ${r_{e}}$. Short distances lead to high repulsion, long distances result in no interactions, and middle distances result in stabilized bonding.

Application of Hooke's Law

Molecules will have some amount of kinetic energy along this degree of freedom and harmonic oscillation will occur along the bond length. A bond between molecules can be approximated as a parabola centred around the equilibrium bond length ${r_{e}}$. Hooke's Law treats the bond as a spring. When a bond is stretched or compressed its potential energy increases, just like the behaviour of a spring under the harmonic oscillation approximation. ${k}$ is the constant corresponding to the stiffness of the spring, called the spring constant, and can be correlated to the stiffness of a molecular bond. Higher spring constants correlate to stiffer (stronger) bonds. For example, the value of ${k}$ will be larger for a double bond than in a single bond. Hence, a double bond is more stiff.

We can approximate the bond as a parabola centred around the equilibrium bond length ${r_{e}}$:

${\mathcal {V}}(r)={\frac {1}{2}}k_{bond}\left(r-r_{eq}\right)^{2}$

Quantum Harmonic Oscillator Approximation

Internuclear separation with respect to bond length.

There are several significant approximations associated with describing chemical bonds as harmonic oscillators:

1. The bond can never dissociate. In reality if we keep pulling two atoms apart the bond will eventually break, but according to the quantum harmonic oscillator approximation the potential energy just continues to increase and bonds are not allowed to break. This can be referred to as anharmonic effects; if bonds were really harmonic no chemical reaction would ever take place.
2. The repulsive wall isn't repulsive enough. In reality, short distances are dominated by repulsive interactions. The low potential energy structures of most important molecules are near the minimum energy geometry.
3. The spacing of the vibrational energy levels are exactly equal. However, in reality they become slightly smaller as quantum number ${n}$ increases.

Energy levels of a quantum harmonic oscillator follow:

$E_{n}=h{\nu }\left(n+{1 \over 2}\right)$

where ${h}$ is Planck's Constant (6.626×10⁻³⁴ J s), $\nu$ is the vibrational frequency of the oscillator in s^-1 and quantum number ${n}$= 0,1,2...

$\mu ={\cfrac {m_{1}m_{2}}{m_{1}+m_{2}}},\!\,$

${v}$ is related to the spring constant, ${k}$, and reduced mass of a diatomic,${\mu }$.

$v={1 \over {2\pi }}{\sqrt {k \over {\mu }}}\!$

Other Important Formulae

Since Planck's constant, $h$, and vibrational frequency, $\nu$, are related by $E=h\nu$, the relation can also be expressed as: $E={\frac {hc}{\lambda }}.$

Wavenumbers, also called vibrational frequency, are reported in reciprocal distance and chemists typically use reciprocal centimetres.

$v={\frac {1}{\lambda }}={\frac {E}{hc}}$

where ${E}$ is Energy in Joules, ${c}$ is the speed of light (2.9979×10⁸ m/s = 2.9979×10¹⁰ cm/s) and, ${\lambda }$ is wavelength. This molecular transition energy is usually extremely small and typically follows the order of 1×10⁻²⁰ joules, J.

Vibrational Zero Point Energy

The ground state does not have zero energy. This is the vibrational zero-point energy, and is consistent with the Heisenberg Uncertainty principle. If a molecule had zero vibrational energy it would be at rest at the minimum, and therefore we would know its position and momentum completely. Even in the lowest energy state, molecules still vibrate.

$E_{n=0}=h\nu \left(n+{1 \over 2}\right)=h\nu \left(0+{1 \over 2}\right)={1 \over 2}h\nu$

Vibrational Absorption Spectra

Vibrational transitions follow the selection rule $\Delta n=\pm 1$, and therefore all vibrational transitions have exactly the same energy.

$\Delta E=h{\nu }\left((n'+1)+{1 \over 2}\right)-h{\nu }\left(n'+{1 \over 2}\right)$

$\Delta E=h{\nu }\left((n'+1)+{1 \over 2}-(n'+{1 \over 2})\right)$

$\Delta E=h{\nu }(1)=h{\nu }$

The vibrational spectrum of diatomics is coupled with rotational transitions. The total selection rule is $\Delta n=\pm 1$ and $\Delta J=\pm 1$.

Vibrational States of Polyatomics

While monatomic gaseous atoms have a vibrational degree of freedom of zero, polyatomic molecules will have several vibrational degrees of freedom. These vibrations are treated as independent harmonic oscillators. Polyatomic molecules are divided into two categories: Linear and non-linear molecules.

For linear molecules: ${\textstyle n_{vib}=3N_{atom}-5}$

For non-linear molecules: $n_{vib}=3N_{atom}-6$

Trends in Vibrational Frequencies

• Strong bonds are stiff bonds, which have a large spring constant ($k$).
• Stiff bonds have large vibrational energy level spacings.

• Light atoms give small reduced masses (${\mu }$).
• Molecules with small reduced masses have large vibrational energy level spacings.

Vibrational Energy Example 1

The harmonic vibrational frequency of HF in wavenumbers is 4141.3 cm^-1.

Using this information, calculate the energy for the transition of HF from the ground to first excited vibrational state.

Solution

Vibrational energy levels of a quantum harmonic oscillator follow:

$E_{n}=h{v}\left(n+{1 \over 2}\right)$

However, this relationship requires the vibrational frequency to be in units of s^-1. To do this, we multiply the given value of 4141.3 cm^-1 by the speed of light, in centimetres.

$v={\widetilde {v}}c$$v=(4141.3cm^{-1})(2.9979\times 10^{10}cm/s)$

$v=1.2415\times 10^{14}s^{-1}$

Now that we have the correct units, the ground state vibrational energy can be calculated as follows:

$E_{0}=h{v}\left(n+{1 \over 2}\right)=h{v}\left(0+{1 \over 2}\right)={1 \over 2}h{v}$

$E_{0}=\left({1 \over 2}\right)(6.626\times 10^{-34}Js)(1.2415\times 10^{14}s^{-1})$

$E_{0}=4.1131\times 10^{-20}J$

Next, the first excited state vibrational energy is:

$E_{1}=h{v}\left(n+{1 \over 2}\right)=h{v}\left(1+{1 \over 2}\right)={3 \over 2}h{v}$

$E_{1}=\left({3 \over 2}\right)(6.626\times 10^{-34}Js)(1.2415\times 10^{14}s^{-1})$

$E_{1}=1.2339\times 10^{-19}J$

Finally, the energy for the transition from the ground state (n=0) to the first excited state (n=1) level is:

$\Delta E=E_{1}-E_{0}$

$\Delta E=1.2339\times 10^{-19}J-4.1131\times 10^{-20}J$

$\Delta E=8.2259\times 10^{-20}J$

Vibrational Energy Example 2

Calculation of the vibrational wavenumber of CO from the force constant and reduced mass.

Harmonic Oscillator Approximation

As there is some kinetic energy along the vibrational degree of freedom, the bond length undergoes oscillation. The Schrӧdinger equation for the movement of quantum mechanical particles given the potential energy function V(r) is complicated to solve. Instead, the Harmonic Oscillator Approximation is used which proposes that the bond behaves like a spring governed by Hooke's law.

Hooke's law: ${\mathcal {V}}(r)={\frac {1}{2}}k(r-r_{eq})^{2}$ where r is the internuclear distance and k is a constant corresponding to the stiffness of the spring

Given this approximation, the following relationship arises

$\nu ={1 \over {2\pi }}{\sqrt {k \over {\mu }}}\!$

where,

• $k$ is the force constant of the bond in ${\textrm {kg}}\ {\textrm {s}}^{-1}$
• $\mu$ is the reduced mass in kilograms
• $v$ is the vibrational frequency of the oscillator in $s^{-1}$

The reduced mass ${\mu }$ for a heteronuclear diatomic can be calculated as follows

${\mu }$ $={\cfrac {m_{1}m_{2}}{m_{1}+m_{2}}}$ where $m_{1}$ and $m_{2}$ corresponds to the masses of each atom.

Solution

Firstly, the reduced mass of the carbon monoxide molecule must be calculated given that the atomic masses of carbon and oxygen is $12.0107u$ and $15.9994u$ respectively.

$\mu ={\cfrac {m_{1}m_{2}}{m_{1}+m_{2}}}$

$\mu ={\cfrac {(12.0107\ u)(15.9994\ u)}{12.0107\ u+15.9994\ u}}$

$\mu ={\cfrac {192.164\ u^{2}}{28.0101\ u}}$

$\mu =6.8605\ u$

Convert into units of kilogram as follows

$\mu =(6.8605\ u)\left({\cfrac {1\ kg}{1000\ g}}\right)\left({\cfrac {1}{6.02214129\times 10^{23}\ mol^{-1}}}\right)$

$\mu =1.1392\times 10^{-26}\ kg$

The next step is to derive the vibrational frequency in $s^{-1}$ given the value of the reduced mass,$\mu =(1.1392)(10^{-26})kg$ , and the force constant $k=1860Nm^{-1}$ . Note that $1\ N\ m^{-1}=1\ kg\ s^{-2}$

$\nu ={1 \over {2\pi }}{\sqrt {k \over {\mu }}}\!$

$\nu ={1 \over {2\pi }}{\sqrt {1860kg/s^{2} \over {1.1392\times 10^{-26}\ kg}}}\!$

$\nu =(0.15915)({\sqrt {(1.6327\times 10^{29})\ s^{-2}}}\!$

$\nu =(0.15915)(4.0407\times 10^{14})\ s^{-1}\!$

$\nu =6.4308\times 10^{13}\ s^{-1}\!$

Convert the vibrational frequency into wavenumbers given the following relationship

${\tilde {v}}={\cfrac {vibrationalfrequency,v\ (s^{-1})}{\textrm {speedoflight}}}$

${\tilde {v}}={\cfrac {6.4308\times 10^{13})\ s^{-1}}{\textrm {speedoflight}}}\!$

${\tilde {v}}={\cfrac {6.4308\times 10^{13}s^{-1}}{2.99792458\times \ 10^{10}cm\ s^{-1}}}\!$

${\tilde {v}}=2145.1\ cm^{-1}\!$

Electronic energy

Atoms and molecules can hold different energy levels that correspond to different distributions in how the electron density is distributed around them. These are counted as electronic degrees of freedom.

For example, the simplest atom is the hydrogen atom, with 1 proton and 1 electron. The attraction between the proton and electron in the hydrogen atom is governed by Coulomb's Law,

principal quantum number	n=1,2,3,...
angular momentum quantum number	$l=0,1,...,n-1$
magnetic quantum number	$m_{l}=-l,-l+1,...,0,l-1,l$
spin quantum number	$m_{s}=+{\frac {1}{2}},-{\frac {1}{2}}$

${\mathcal {V}}(r)=-{\frac {e^{2}}{4\pi \epsilon _{0}r}}$

Where $e$ is the elementary charge of an electron, $r$ is the distance between the proton and electron in the hydrogen atom, and $\epsilon _{o}$ is the vacuum permittivity constant. When the Schrödinger equation is solved for this potential, four quantum numbers result, n, l, m_l, and m_s. This means that the particles can only take on certain discrete values of energy. The electronic energy of the hydrogen atom depends only on the principal quantum number $n$ via the following equation,

$\epsilon _{n}=-{\frac {m_{e}e^{4}}{32\pi ^{2}\epsilon _{o}^{2}\hbar ^{2}}}{\frac {1}{n^{2}}}$

Where $m_{e}$ is the mass of an electron. This means that all sets of angular momentum, l, and magnetic quantum numbers, m_l, and m_s, with the same value of n are degenerate, as they do not appear in this solution to the Schrödinger equation. This quantization of allowed energies give rise to the electronic energy levels of the hydrogen atom. This equation can also be used to calculate the energy levels of hydrogen like species such as He⁺. An atomic factor, $Z^{2}$, would be added in the numerator to account for the extra protons in the atom, which would pull the electrons in more than the hydrogen atom, and thereby increase the energy.

Example

Calculation of the energy for the excitation of O₂ from the triplet to singlet electronic state.

Singlet oxygen comes from the electronic excitation of triple oxygen, the energy is experimentally 0.98 electron volts per mole of electrons. The figure below illustrates the different states of oxygen. ¹Δ_g and ¹Σ_g⁺ represents singlet oxygen as it has a spin state equal to one, the triplet degenerate state is represented by ³Σ_g^-, the transition is represented by ¹Δ_g←³Σ_g^-

source: Singlet Oxygen-Singlet Oxygen

The degeneracy is calculated for this state is calculated from the formula g_el= 2S+1 where S is the sum of the spin of the electrons. For singlet oxygen it has one spin state of -1/2 and a spin state of +1/2 giving the sum to be 0 and the degeneracy to be calculated by g_el= 2(0)+1 to give a degeneracy of 1. Triple oxygen has two electrons in the spin up state to give it a value of 1. Which gives the degeneracy of 3 for this state.

The experimental value for this transition is experimentally calculated to be 0.98 eV found on Singlet Oxygen. This is for a wavelength of 1270 nm. the conversion factor from eV (electron volts) to kJ/mol is given by multiplying the number of electron volts by 96 kJ/mol, for the transition of triplet degenerate state to the singlet energy state it gives a value of 94.56 kJ/mol.

Raman spectroscopy

The Raman Effect

Examples of energy transitions for each type of Raman line

The Raman effect is a form of light scattering by a material. It can be observed when a sample is exposed to an intense, high energy, monochromatic light source, such as a laser. Most photons of this light that are scattered by the material will be scattered elastically, meaning that there will be no change in the frequency of light. This results in an intense line at the same frequency of the source, known as the Rayleigh line.

Photons can also undergo Raman scattering, where they are inelastically scattered. This means that they will emerge at a higher or lower frequency. This type of scattering is less common than elastic scattering, with only 1 in 10⁷ photons experiencing Raman scattering. Stokes lines occur when the scattered light emerges at a lower frequency. Anti-stokes lines occur when the scattered light emerges at a higher frequency.

The Raman effect is applicable even when the frequency of radiation does not correspond to a transition between molecular energy levels. This cannot be explained by standard absorption or emission and therefore must be the Raman effect.

Raman Spectroscopy

Raman spectroscopy is a spectroscopic technique which measures inelastic scattering. The gain or loss of energy by incident light corresponds to transitions between the energy levels of the molecules. These transitions are both rotational and vibrational. A high energy photon excites a molecule to a "virtual state" (v₁), following this the molecule returns to a different state (v₂) on emission. A different frequency of light is emitted due to the difference in initial and final energy levels.

The Gross Selection Rule for Raman Spectroscopy

The gross selection rule for Raman spectroscopy states that a molecule must be anisotropically polarizable to have a Raman spectrum. Anisotropic indicates that something is different in some directions, in this case the electron density of the molecule must be polarized heterogeneously allowing for it to be observed via Raman spectroscopy.

Examples of some molecules which are spherical tops

This selection rule explains why Raman spectroscopy can successfully analyze homonuclear diatomics, such as H₂ and N₂, when rotational and vibrational spectroscopic techniques cannot.

The Raman effect is present for any molecule that can be polarized anisotropically. Molecules that are spherical tops cannot be anisotropically polarized, this is because they have three equal moments of inertia. Therefore these molecules cannot be observed using Raman spectroscopy.

The Specific Selection Rule of Rotational Raman Spectroscopy

The specific selection rule for Raman spectroscopy of linear molecules is $\Delta J=0,\pm 2$. The Raman spectrum has regular spacing of lines, as seen previously in absorption spectra, but separation between the lines is doubled. The evenly spaced lines have a separation of: ${\widetilde {v}}=4{\widetilde {B}}(J+1)$ where: ${\widetilde {B}}={\frac {h}{8\pi ^{2}cI}}$

The rotational energy of the molecule can be calculated using the following equation: $E_{rot}={\frac {h^{2}}{4\pi ^{2}\mu r_{e}^{2}}}J(J+1)$

The Specific Selection Rule of Vibrational Raman Spectroscopy

The specific selection rule for vibrational Raman spectroscopy states that only Δv = ±1 transitions are allowed. This is the same as for vibrational absorption spectroscopy. Vibrational Raman transitions occur simultaneously with rotational Raman transitions, this results in branching caused by rotational transitions in the Δv = ±1 peaks. The vibrational transitions result in 3 branches with fine structure from rotational transitions. In the spectrum each line corresponds to a change in quantum numbers v, J, or both.

Branch	Energy Level Transition
O	ΔJ=-2
Q	ΔJ=0
S	ΔJ=2

Raman Spectroscopy Example 1

Calculation of rotational energy levels of N₂ from pure rotational Raman spectrum.

For a molecule to have a Raman spectrum it must be anisotropically polarizable and thus have a different electron cloud distortion along different axis. Given the Pure Rotational Raman Spectrum of a molecule it is possible to calculate the rotational energy levels based on the spectrum itself. Transitions of $\Delta J=\pm 1$ can be observed in the spectrum and used to find the energy levels.

A sample calculation to find the rotational energy levels of Nitrogen can be computed using the spacings and J values of the Raman spectrum below. This calculation will be done in three steps:

1. Finding the rotational constant, ${\widetilde {B}}$.

2. Finding the moment of Inertia, $I$.

3. Finding the rotational energy, $E_{rot}$.

Step 1: Computing the rotational constant B:

As seen from the figure above, the spacing, or v, is approximately 8.00 cm^-1 which corresponds to the quantum number J = 1. Using these values it is possible to compute B by re-arranging the formula below:

${\widetilde {\nu }}=4{\widetilde {B}}(J+1)$

${\widetilde {B}}={\frac {\widetilde {\nu }}{4(J+1)}}$

${\widetilde {B}}={\frac {8.00cm^{-1}}{4(1+1)}}$

${\widetilde {B}}=1.00cm^{-1}$

Step 2: Compute the moment of Inertia I using the formula below and the constant B determined above:

${\widetilde {B}}={\frac {h}{8\pi ^{2}cI}}$

$I={\frac {h}{8\pi ^{2}c{\widetilde {B}}}}$

Note: h is Planck's constant $6.62607004\times 10^{-34}J/s$ and c is the speed of light in cm/s: $2.99792458\times 10^{10}cm/s$. When using frequencies in units of wavenumber ($cm^{-1}$), the speed of light in units of cm/s should be used in order for them to cancel out during the calculation.

$I={\frac {6.626\times 10^{-34}J/s}{8\pi ^{2}(2.998\times 10^{10}cm/s)(1.00cm^{-1})}}$

$I=2.799\times 10^{-46}kg/m^{2}$

Step 3: Compute the rotational energy level using the value of I from above and the following two equations:

$I=\mu r_{e}^{2}$

$E_{rot}={\frac {h}{4\pi \mu r_{e}^{2}}}J(J+1)$

Note: Substituting the equation for I into the energy equation will give:

$E_{rot}={\frac {h^{2}}{4\pi ^{2}I}}J(J+1)$

$E_{rot}={\frac {(6.626\times 10^{-34}J/s)^{2}}{4\pi ^{2}(2.799\times 10^{-46}kg/m^{2})}}1(1+1)$

$E_{rot}=3.94\times 10^{-23}J$

Note: Since the calculated value of $E_{rot}$ was done using $J=1$, this corresponds to the energy of the $J=1$ energy level. This calculation can be repeated using different values of $J$ to determine the different energies of each rotational energy level.

Postulates of Statistical Thermodynamics

Postulates of Statistical Thermodynamics

Statistical thermodynamics is a branch of science which utilizes statistics in order to relate the microscopic properties of a system to the macroscopic properties. Classical thermodynamics describes macroscopic properties of a system composed of atoms or molecules such as pressure, enthalpy and internal energy. On the other hand, quantum mechanics utilizes quantized values of microscopic properties of a system, such as rotational and vibrational movement, to calculate the energy of the system. Using two different methodologies, both thermodynamics and quantum mechanics can be utilized to evaluate similar properties of a system without any clear connection between the two fields. Statistical thermodynamics provides this connection by averaging the microscopic values across a large set of microcanonical ensembles at an instant in time to arrive at macroscopic values. These microcanonical ensembles are physical systems in which the volume, energy and total number of particles are held constant. The total number of microcanonical ensembles (𝒜), can be averaged to obtain a mean result, known as the mechanical value.

First Postulate of Statistical Thermodynamics

The First Postulate of Statistical Thermodynamics states that the time average of a mechanical variable M in the thermodynamic system of interest is equal to the ensemble average of M as the limit of 𝒜 → ∞. This law states that the average value of a mechanical variable taken from the ensembles of microstates matches the mechanical value predicted by classical thermodynamics, so long as the number of microstates 𝒜 is an exceedingly high number. The First Postulate of Statistical Thermodynamics can be extended to arrive at the Gibbs Postulate, which relates the energy of said microstates to internal energy of a system as calculated by classical thermodynamics.

Gibbs's Postulate

Gibbs's Postulate relates the internal energy (U) of a system, determined by thermodynamics, to the average ensemble energy (E), determined by statistical mechanics.

$U=\langle E\rangle$

The average energy over the 𝒜 copies in the ensemble is given by the following equation.

$\langle E\rangle ={\frac {1}{A}}\sum _{i}^{A}E^{i}$

$E^{i}=hv(n_{1}^{i}+n_{2}^{i}+n_{3}^{i}+...)$

Through the Gibbs Postulate, the average ensemble energy can be used to define the thermodynamic values of Helmholtz energy ($A$), entropy ($S$), pressure ($p$), and thermodynamic potential ($\mu$) through the following relationships.

${A=U-TS}$

${S=-\left({\frac {\partial A}{\partial T}}\right)_{N,V,}}$

${p=-\left({\frac {\partial A}{\partial V}}\right)_{N,T,}}$

${\mu =\left({\frac {\partial A}{\partial N}}\right)_{T,V,}}$

Second Postulate of Statistical Thermodynamics

The Second Postulate of Statistical Thermodynamics states that for an ensemble representative of an isolated system, the systems of the ensemble are distributed uniformly. All states consistent with the specified microcanonical system will occur with equal probability. This is otherwise known as the principle of equal 'a priori' probabilities. For example, in two microcanonical systems with three particles capable of occupying a quantum level $n$, with $n=0,1,2,3...$, there is an equal probability of the first system occupying the states $n_{1}=1,n_{2}=0,n_{3}=2$, as there is the second system occupying the states $n_{1}=6,n_{2}=4,n_{3}=9$. Across the distribution for each system there is an indiscriminate occupation of each quantum state which is just as likely as any other.

Microcanonical ensemble

A microcanonical ensemble is a statistical ensemble which is used to represent the possible states of a mechanical system in which the total energy of the system is exactly specified. A micro-canonical ensemble is assumed to be isolated, thus the system cannot exchange energy or particles with the environment. The system, which can be composed of a solid, liquid or a gas is completely isolated from its surroundings and has constant energy (E), number of particles (N), and volume (V). This ensemble composes of an assembly of “copies” of this isolated system; the energy of each copy is the same, thus E=U, considering one copy of this system is sufficient.

Combinatorial Mathematics

Even though the energy of each copy of the system in a microcanonical ensemble is the same, these copies can exist in different quantum states. For example, consider a system composed of 2 hydrogen molecules, with the total vibrational energy of 2hυ.

$E_{vib}=\sum _{i}n_{i}h\nu =2h\nu$

$\sum _{i}n_{i}=2$

The vibrational quantum numbers must add up to 2, however, there are, in fact, three ways of achieving this. Two possible configurations are where one molecule has n = 2, and the other has n = 0; and the third configuration is where both molecules have n = 1.

It can be noted that in the example above that the three configurations (also called microstates) form two macrostates (states with unique sets of quantum numbers) - {0,2} with a weight of 2 (because there are two ways of arriving at this configuration), and {1,1} with a weight of one. The weights of these states play an important role in Statistical Mechanics, so it is important to know a way to quickly determine them, rather than just counting them directly.

Let's consider the weights of configurations {1,2}, {1,2,3} and {1,2,3,4}. Counting the weights gives 2, 6 and 24 or 2!, 3! and 4! respectively for these three states where

$n!=1\cdot 2\cdot 3\cdot ...\cdot n$

represents factorial of the number n. The weights of the configurations are just permutations or ways a given set of the quantum numbers can be arranged. Using combinatorial mathematics, the weight of a certain vibrational state in the example above can be found to be

$W(n_{1},n_{2},n_{3},...)={\frac {N!}{n_{1}\cdot n_{2}\cdot n_{3}\cdot ...}}={\frac {N!}{\prod _{i}n_{i}!}}$

where N is the total number of molecules and n_i is the number of molecules in the state i.

Generalizing, the weight of a system with occupancies $a_{1},a_{2},a_{3},...$ in an ensemble containing ${\mathcal {A}}$ systems is

$W(a_{1},a_{2},a_{3},...)={\frac {{\mathcal {A}}!}{a_{1}\cdot a_{2}\cdot a_{3}\cdot ...}}={\frac {{\mathcal {A}}!}{\prod _{i}a_{i}!}}$

Example

If there are three molecules and four units of vibrational energy, what are the possible macrostates of this system and what is the weight of each macrostate?

A number of microstates in the same system can have the same composition. These systems can be weighted depending on the occupancies of the systems. The weight of a macrostate can be defined by the equation:

$W(a_{1},a_{2},a_{3},..)={\frac {{\mathcal {A}}!}{\prod _{i}a_{i}!}}$

Where, ${\mathcal {A}}!$ represents the total number of systems in the ensemble and $\prod _{i}a_{i}!$ represents the product of the factorial of the occupancies of each level.

For three molecules with four units of vibrational energy, we have four unique ways to distribute the four units of vibrational energy between the three molecules, {0,0,4}, {0,1,3}, {1,1,2} and {0,2,2,}. So for this example, ${\mathcal {A}}$ = 4 and the weights of each variation of the system would then be:

$W(0,0,4)={\frac {{\mathcal {A}}!}{\prod _{i}a_{i}!}}={\frac {4!}{4!0!0!}}=1$

$W(0,1,3)={\frac {{\mathcal {A}}!}{\prod _{i}a_{i}!}}={\frac {4!}{0!1!3!}}=4$

$W(1,1,2)={\frac {{\mathcal {A}}!}{\prod _{i}a_{i}!}}={\frac {4!}{1!1!2!}}=12$

$W(0,2,2)={\frac {{\mathcal {A}}!}{\prod _{i}a_{i}!}}={\frac {4!}{0!2!2!}}=6$

References

University of Delaware.http://www.physics.udel.edu/~glyde/PHYS813/Lectures/chapter_6.pdf (accessed Feb 24, 2017).

Balakrishnan, V. The Microcanonical Ensemble, 2017.

Boltzmann Distribution

Developing the Canonical Ensemble

The first step is to develop a model of how the energy is distributed; the model which will be used is a canonical ensemble which is a system at constant number of particles, volume and temperature. A canonical ensemble can be created by first taking a microcanonical ensemble of a large number of systems, ${\mathcal {A}}$, all at the same number of particles, volume and energy. The entire microcanonical ensemble is then immersed into a heat bath. The systems are then allowed to exchange energy with the heat bath until all the systems come to a thermal equilibrium. The microcanonical ensemble is the removed from the heat bath such that the systems can only exchange energy with the other systems around it. The systems will now have a distribution of all possible total energies. These energy states can then be numbered in increasing energy (i.e., lowest energy is $E_{1}$). Since each of these energy states can have any number of systems with that energy, then the number of systems with total energy $E_{i}$ can be defined as the occupation of the state $i$ with variable $a_{i}$. The entire ensemble can then be defined as the occupancies of the energy states, where the total number of systems, ${\mathcal {A}}$, is:

$\Sigma _{i}a_{i}={\mathcal {A}}$

and the total energy of the entire ensemble, or energy level, $\varepsilon$, is:

$\Sigma _{i}a_{i}E_{i}=\varepsilon$

The Weight of a Configuration

The occupancy of any of these energy levels depends on how many possible ways the total energy of the ensemble can be distributed amongst the systems or can be described by the occupancies of the energy states. Some of these configurations of the occupancies are mathematically more likely than others.

The weight of a configuration, or the number of ways to distribute the energy of the ensemble, is important. By combinatorial mathematics the weight of a system with occupancies $a_{1},a_{2},a_{3},...$ in an ensemble containing ${\mathcal {A}}$ systems is:

$W(a_{1},a_{2},a_{3},...)={\frac {{\mathcal {A}}!}{a_{1}!a_{2}!a_{3}!...}}={\frac {{\mathcal {A}}!}{\Pi _{i}a_{i}!}}$

System Weighting

Consider an ensemble of ${\mathcal {A}}$ systems divided into two states. The occupancy of the first state is N and therefore the occupancy of the second state is A-N. The weight of this configuration as a function of N is:

$W(N)={\frac {{\mathcal {A}}!}{N!({\mathcal {A}}-N)!}}$

It can be shown that as ${\mathcal {A}}$ increases the most probable distribution (N=${\mathcal {A}}$ /2) becomes much more heavily weighted than any other configuration.

The Most Probable Distribution

To describe a canonical ensemble, only the most probable set of occupancies need to be determined, denoted as a*. For a very large ${\mathcal {A}}$, the configuration with the largest weight will be much more heavily weighted than the other configurations. Therefore, this set of occupancies will be the most probable, and any configuration with a significantly large weight will be close to a*.

However, for any given ensemble, not all occupancies are possible. This is due to the imposition of constraints upon the occupancies by the specific ensemble. In a canonical ensemble there are two constraints which were previously used to define a canonical system:

1. The sum over all energy levels has to add up to the total energy of the ensemble, denoted as $\varepsilon$ :$\Sigma _{i}a_{i}E_{i}=\varepsilon$
2. The sum of all of the occupancies must be equal to ${\mathcal {A}}$ :$\Sigma _{i}a_{i}={\mathcal {A}}$ Therefore, given these two constraints, we must find a* that agrees with the above imposed constraints of the canonical ensemble.

Calculating the Most Probable Occupancy

To calculate the most probable occupancy, we must calculate the occupancies that would give the maximum weight. Lagrange multipliers are used to maximize this function.

Mathematical Manipulation of W

It was previously given that $W(a_{1},a_{2},a_{3},...)={\frac {{\mathcal {A}}!}{a_{1}!a_{2}!a_{3}!...}}={\frac {{\mathcal {A}}!}{\Pi _{i}a_{i}!}}$ However, this equation is difficult to manipulate. But, for a positive function, the maximum occurs at the same location as it does in the natural logarithm of the function. Since the maximum is what we’re really interested in finding, we can use $\ln {W}$ to find the maximum, which makes the mathematics easier to manipulate. Therefore the equation becomes:

$\ln {W}(a_{1},a_{2},a_{3},...)=\ln {\left({\frac {{\mathcal {A}}!}{\Pi _{i}a_{i}!}}\right)}$

$=\ln {{\mathcal {A}}!}-\ln {\Pi _{i}a_{i}!}$

$=\ln {{\mathcal {A}}!}-\Sigma _{i}\ln {a_{i}!}$

Applying the Math to a Canonical Ensemble

Using the Lagrange multipliers as previously described, we can determine the most probable occupancy of the canonical system. When Lagrange multipliers are applied to the $\ln {W}$ equation, following the aforementioned constraints, the new equation becomes:

${\frac {\partial }{\partial a_{j}}}\left[\ln W(a_{1},a_{2},a_{3}...)-{\alpha }[({\Sigma _{i}a_{i}})-{\mathcal {A}}]-{\beta }[({\Sigma _{i}a_{i}E_{i}})-{\varepsilon }]\right]=0$

Next, we must simplify each of the three terms in the equation and solve for the unknown constants $\alpha$ and $\beta$.

Term 1

${\frac {\partial }{\partial a_{j}}}\ln W(a_{1},a_{2},a_{3}...)={\frac {\partial }{\partial a_{j}}}\ln {{\mathcal {A}}!}-\ln {\Pi _{i}a_{i}!}=-{\frac {\partial }{\partial a_{j}}}\ln {a_{j}!}$

Using Stirling’s Approximation:

$-{\frac {\partial }{\partial a_{j}}}\ln {(a_{j}!)}=-{\frac {\partial }{\partial a_{j}}}[{a_{j}}\ln {(a_{j})}-{a_{j}}]={-a_{j}}{\frac {1}{a_{j}}}-\ln {(a_{j})}+{1}=-\ln {(a_{j})}$

Term 2

${\frac {\partial }{\partial a_{j}}}\alpha [(\Sigma _{i}a_{i})-{\mathcal {A}}]$

For ${\Sigma _{i}a_{i}}$ , there will be one term of the sum where i = j, everything else is equal to zero. Therefore, this term becomes:

${\frac {\partial }{\partial a_{j}}}{\alpha }{a_{j}}={\alpha }$

Term 3

${\frac {\partial }{\partial a_{j}}}{\beta }[({\Sigma _{i}a_{i}E_{i}})-{\varepsilon }]$

Like term 2, for ${\Sigma _{i}E_{i}}$ , there will be one term of the sum where i = j, everything else is equal to zero. Therefore, this term becomes:

${\frac {\partial }{\partial a_{j}}}\beta {E_{j}a_{j}}=\beta {E_{j}}$

Now that the three terms have been simplified, we can combine them into one equation to solve. This gives us:

$-\ln {(a_{j})}-{\alpha }-{\beta }{E_{j}}=0$

Solving for ${a_{j}}$ gives:

${a_{j}}={e^{-\alpha }}{e^{-{\beta }{E_{j}}}}$

Determining $\alpha$ and $\beta$

The next step of the derivation is to determine the constants $\alpha$ and $\beta$.

We can use one of the constraints to determine $\alpha$.

$a_{i}={e^{-\alpha }}{e^{-\beta {E_{i}}}}$

$\Sigma _{i}a_{i}={\mathcal {A}}$

${\Sigma _{i}}{e^{-\alpha }}{e^{{-\beta }{E_{i}}}}={\mathcal {A}}$

${e^{-\alpha }}{\Sigma _{i}}{e^{{-\beta }{E_{i}}}}={\mathcal {A}}$

${e^{\alpha }}={\frac {1}{\mathcal {A}}}{\Sigma _{i}}{e^{{-\beta }{E_{i}}}}$

Using this equation and the constraint, we can define the probability of a system in the ensemble as the occupation of state i divided by the total number of systems in the ensemble, which can be represented by the following equation.

${P_{i}}={\frac {a_{i}}{\mathcal {A}}}={\frac {e^{{-\beta }{E_{i}}}}{{\Sigma _{i}}{e^{{-\beta }{E_{j}}}}}}$

Determining $\beta$ requires connecting it to classical thermodynamics. We can determine the average of a variable (<M>) over the states of a system by employing the equation

$\langle M\rangle ={M_{i}}{P_{i}}$

The average energy is

$\langle E\rangle ={\frac {{\Sigma _{j}}{E_{j}}{e^{{-\beta }{E_{j}}}}}{{\Sigma _{i}}{e^{{-\beta }{E_{j}}}}}}$

The average pressure is

$\langle p\rangle ={\frac {{\Sigma _{j}}-\left({\frac {\partial E_{j}}{\partial V}}\right)_{N}{e^{{-\beta }{E_{i}}}}}{{\Sigma _{i}}{e^{{-\beta }{E_{j}}}}}}$

Knowing these equations and combining two other equations we can come up with the following equation, which can be compared to a classical thermodynamic equation shown below.

$\left({\frac {\partial \langle E\rangle }{\partial V}}\right)_{N,{\beta }}+{\beta }\left({\frac {\partial \langle p\rangle }{\partial {\beta }}}\right)_{N,V}=-\langle p\rangle$

$\left({\frac {\partial U}{\partial V}}\right)_{T,N}-{T}\left({\frac {\partial p}{\partial T}}\right)_{N,V}=-{p}$

In order to better compare the equations, we can perform a calculation such that the signs in front of ${\beta }$ and T are the same, giving the following equations:

$\left({\frac {\partial \langle E\rangle }{\partial V}}\right)_{N,{\beta }}+{\beta }\left({\frac {\partial \langle p\rangle }{\partial {\beta }}}\right)_{N,V}=-{\langle p\rangle }$

$\left({\frac {\partial U}{\partial V}}\right)_{T,N}+{\frac {1}{T}}\left({\frac {\partial p}{\partial {\frac {1}{T}}}}\right)_{N,V}=-p$

Since multiplying through by a constant would not change the equations, we can determine that ${\beta }$ is only proportional to ${\frac {1}{T}}$.

$\beta \propto {\frac {1}{T}}$

We can introduce ${k_{B}}$ as a proportionality constant to convert the proportionality to an equation as follows:

$\beta ={\frac {1}{k_{B}T}}$

The Boltzmann Distribution

Earlier we determined the probability of a state within a system. Now that we know ${\alpha }$ and ${\beta }$, we can complete the equation to determine the Boltzmann Distribution.

${P_{i}}={\frac {a_{i}}{\mathcal {A}}}={\frac {e^{-\beta E_{i}}}{\sum _{i}e^{-\beta E_{j}}}}={\frac {e^{-E_{i}/{k_{B}T}}}{\sum _{i}e^{-E_{i}/{k_{B}T}}}}$

Example

Consider a system with two singly-degenerate energy levels separated by $10^{-21}$ J. Derive an equation for the probability of the system being in the ground state. Plot the probability of the system being in the ground state between temperatures 1 K and 1000 K.

${P_{i}}={\frac {a_{i}}{\mathcal {A}}}={\frac {e^{-\beta E_{i}}}{\sum _{i}e^{-\beta E_{j}}}}={\frac {e^{-E_{i} \over {k_{B}T}}}{\sum _{i}e^{-E_{i} \over {k_{B}T}}}}$

$k_{B}=1.380\times 10^{-23}{J \over k}$ is the Boltzmann constant in joules per Kelvin. The ground state has an energy level of zero (${E_{o}=0}$). Since the ground energy level is known and the difference between the ground energy level and the first high energy level is given (∆E = $10^{-21}$J), the high energy level can be determined using the following equation:

${\Delta E=E_{1}-E_{0}}$

After using the actual values, the equation should look like this

${10^{-21}=E_{1}-0}$

${E_{1}=10^{-21}}$

The probability equation can then be simplified to the following:

${P_{i}}={\frac {e^{-E_{i} \over {k_{B}T}}}{e^{-E_{i} \over {k_{B}T}}+{e^{-E_{i} \over {k_{B}T}}}}}$

${P_{0}}={\frac {e^{-E_{0} \over {k_{B}T}}}{e^{-E_{0} \over {k_{B}T}}+{e^{-E_{1} \over {k_{B}T}}}}}$

After substituting the values determined into the equation, the probability equation should be the following:

${P_{0}}={\frac {e^{0 \over {k_{B}T}}}{e^{0 \over {k_{B}T}}+{e^{{\Biggl (}{-(10^{-21}) \over {1.380\times 10^{-}23{\bigl (}{J \over K}{\bigr )}\times T}}{\Biggr )}}}}}$

Since the $e^{0}=1$, the equation can be simplified to

$P_{0}={\frac {1}{1+{e^{{\Biggl (}{-(10^{-21}) \over {{1.380\times 10^{-23}{\bigl (}{J \over K}{\bigr )}}\times T}}{\Biggr )}}}}}$ Note: The probability does not have units.

This equation can be used to determine the probability of the system as the temperature changes in Kelvin.

Zoomed in graph of the probability of the Boltzmann distribution over the change of temperature in Kelvin

The probability of the system, which starts from one, gradually decreases as the temperature increases. the reason why can be observed from the equation. Since the temperature is in the denominator, the probability should be smaller as the denominator increases. After about 300 k, the line pattern starts to have a slight decrease toward 0.5 of probability. In other words, the probability of Boltzmann distribution at this system becomes less probable as the temperature exceeds 1000 K.

Molecular partition functions

The partition function of a system, Q, provides the tools to calculate the probability of a system occupying state i .Partition function depends on composition,volume and number of particle. Larger the partition function allows to have more accessible energy states at that temperature.The general form of a partition function is a sum over the states of the system,

$Q=\sum _{i}\exp \left({\frac {-E_{i}}{k_{B}T}}\right)$

Two equivalent ways could be used to write the the partition function. Sum over states approach allows to give different indices to the states with the same energy. Energy levels approach suggests that only energy levels with distinct energies have their own index.

This requires that the energies levels of the entire system must be known and the calculations have to be calculated from sums over states. This limits the types of the systems that we can derive properties for.

For ideal gases, we assume that the energy states of molecules are independent of those in other molecules. The molecular partition function, q, is defined as the sum over the states of an individual molecule.

$q=\sum _{i}\exp \left({\frac {-\epsilon _{i}}{k_{B}T}}\right)$

The particles of an ideal gas could be considered distinguishable if they are different from each other and, therefore, the unique label could be assigned to each.On the contrary, the indistinguishable particles are impossible to assign a unique label, as they are the identical to each other.This article considers the indistinguishable particles of an ideal gas for which the partition function of the system (Q) could be expressed in terms of the molecular partition function (q),and the number of particles in the system (N).As the partition function allows to calculate the probability of the system occupying the state j.Such system could be assumed as isolated, as a microcanonical ensemble of particles, where the total volume, the total energy and number of particles are constant. However, the range of energies appropriate for composition, volume and temperature of canonical ensembles contributing to the system must be still considered for composition, volume and temperature.

Partition function of an ideal gas of indistinguishable particles $Q={\frac {q^{N}}{N!}}$

Molecular Partition Functions

The energy levels of a molecule can be approximated as the sum of energies in the various degrees of freedom of the molecule,

$\epsilon =\epsilon _{trans}+\epsilon _{rot}+\epsilon _{vib}+\epsilon _{elec}$

Correspondingly, we can divide molecular partition function (q),

$q=\sum _{i}\exp \left({\frac {-(\epsilon _{trans}+\epsilon _{rot}+\epsilon _{vib}+\epsilon _{elec})}{k_{B}T}}\right)$

$q=\sum _{i}\exp \left({\frac {-\epsilon _{trans,i}}{k_{B}T}}\right)\sum _{i}\exp \left({\frac {-\epsilon _{rot,i}}{k_{B}T}}\right)\sum _{i}\exp \left({\frac {-\epsilon _{vib,i}}{k_{B}T}}\right)\sum _{i}\exp \left({\frac {-\epsilon _{elec,i}}{k_{B}T}}\right)$

$q=\sum _{i}\exp \left({\frac {-\epsilon _{trans,i}}{k_{B}T}}\right)\times \sum _{i}\exp \left({\frac {-\epsilon _{rot,i}}{k_{B}T}}\right)\times \sum _{i}\exp \left({\frac {-\epsilon _{vib,i}}{k_{B}T}}\right)\times \sum _{i}\exp \left({\frac {-\epsilon _{elec,i}}{k_{B}T}}\right)$

$q=q_{trans}\times q_{rot}\times q_{vib}\times q_{elec}$

Translational Partition Function

The translational partition function, q_trans, is the sum of all possible translational energy states, which could be represented using one,two and three dimensional models for a particle in the box equation, depending on the system of the coordinates .The one and two dimensionsal spaces for a particle in the box equation forms are less commonly used than the three dimensional form as those do not account for the force acting on the particles inside of a box. For a molecule in the three dimensional space, the energy term in the general partition function equation is replaced with the particle in a 3D box equation. All molecules have three translational degrees of freedom, one for each axis the molecule can move along in three dimensional space.

Particle in a 3D Box Equation $E_{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8mL^{2}}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})$

The assumption that energy levels are continuous is valid because the space between energy levels is extremely small, resulting in minimal error. This form is convenient as it does not include a sum to infinity and can therefore be solved with relative ease. The translational partition function can be simplified further by defining a DeBroglie wavelength, $\Lambda$, of a molecule at a given temperature.

$q_{trans}={\frac {V}{\Lambda ^{3}}}$

$\Lambda =\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{-1/2}$

Rotational Partition Function

The rotational partition function, $q_{rot}$, is the sum of all possible rotational energy levels. This sum is found by substituting the equation for the energy levels of a linear rigid rotor:

$E_{j}={\frac {\hbar ^{2}}{2\mu r^{2}}}J(J+1),J=0,1,2,...$

Into the partition function, to produce an open form of the rotational partition function:

$q_{rot}=\sum _{j=1}^{\infty }\ g_{i}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)$

By solving this sum using a definite integral from zero to infinity, a closed form of this function can be found, making numerical evaluation much easier:

$q_{rot}={\frac {2k_{B}T\mu r^{2}}{{\text{ħ}}^{2}}}$

The full derivation of the closed form of the rotational partition function of a linear rotor is given here.

The special case of rotational partition function for homonuclear diatomics could cause the lower weight for alternating states,and result in the change of the rotational partition function. This case is based on the assumption that the total wavefunction of the two exchanging nuclei must be either asymmetric for the nuclei with the even spins (integer spins),or symmetric for the nuclei with odd spins. This function applies only to heteronuclear diatomic molecules. However, this equation can be altered by adding a variable to alter the equation based on the nature of the diatomic molecule being studied:

$q_{rot}={\frac {2k_{B}T\mu r^{2}}{\sigma \hbar ^{2}}}$

where $\sigma$ is 1 for heteronuclear diatomics, and 2 for homonuclear diatomics.

The characteristic temperature is the constant that combines many constants calculated for partition functions of rotational and vibrational levels,introducing the fact of partition function dependence on the temperature change. The characteristic temperature is now defined as , $\Theta _{rot}$ where,

$\Theta _{rot}={\frac {\hbar ^{2}}{2k_{B}\mu r^{2}}}$

determining the rotational partition function can be calculated much easier using,

$q_{rot}={\frac {T}{\sigma \Theta _{rot}}}$

Vibrational Partition Function

A Partition Function (Q) is the denominator of the probability equation. It corresponds to the number of accessible states in a given molecule. Q represents the partition function for the entire system, which is broken down and calculated from each individual partition function of each molecule in the system. These individual partition functions are denoted by q. All molecules have four different types of partition functions: translational, rotational, vibrational, and electronic. Looking only at the vibrational aspect of the system, there is a specific unique equation used to calculate its partition function:

The vibrational partition function of a linear molecule is,

$q_{vib}={\frac {1}{1-\exp \left({\frac {-h\nu }{k_{B}T}}\right)}}$

In general, the molecule partition function can be written as an infinite sum. This is called the open form of the equation:

$q=\sum _{j}g_{i}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)$

It is much easier and more convenient to write this as a closed sum. This turns the equation into an approximative algebraic expression, with the following parameters in variables:

• degeneracy $g_{j}=1$
• quantum number $n=1,2,3...$
• energy levels $\varepsilon _{n}=h\nu (n+({\frac {1}{2}}))$

The energy levels, $\Delta E_{J}$ are defined relative to the ground state of the system (i.e., the zero point energy is subtracted from each level),

$\Delta E_{J}=\varepsilon _{j}-\varepsilon _{0}$

$=h\nu (j+{\frac {1}{2}})-h\nu (0+{\frac {1}{2}})=h{\nu }j+{\frac {1}{2}}h{\nu }-{\frac {1}{2}}h{\nu }=h{\nu }j$

By exploring some substitutions and derivations, the equation listed above for a linear molecule is achieved. The substitutions made include:

• $g_{j}=1$
• $E_{j}=h{\nu }j$
• $j=0,1,2...$

At the same time, it is important to note that ${\nu }$ represents the vibrational frequency of the molecule. It can be calculated on its own prior by the following relation:

$v={\frac {1}{2\pi }}\left({\frac {k}{\mu }}\right)^{\frac {1}{2}}$

where k represents the spring constant of the molecule and μ represents the reduced mass of the same molecule.

Electronic Partition Function

The electronic partition function (q_el) of a system describes the electronic states of the system at thermodynamic equilibrium. This can be written as a sum over states,

$q_{el}=\sum g_{j}\exp(-\beta \epsilon _{j})$

however due to high energy levels being present under most circumstances, the electronic partition function can be reduced to:

$q_{el}=g_{0}$

Thus, the electronic partition function can usually be approximated as the ground state degeneracy of the atom or molecule.

Molecular Partition Function

The molecular partition function, q, is the total number of states accessible to the atom or molecule. It is the product of the vibrational, rotational and translational partition functions:

$q=q_{trans}\times q_{rot}\times q_{vib}\times q_{el}$

Sample problems

Problem 1

Calculate the probability of a molecule of N₂ being in the ground vibrational state at 298 K.

The probability that a system occupies a given state at an instant of time and a specific temperature is given by the Boltzmann distribution.

$P_{i}={\frac {\exp \left({\frac {-E_{i}}{k_{B}T}}\right)}{\sum _{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)}}$

$P_{i}={\frac {\exp \left({\frac {-E_{i}}{k_{B}T}}\right)}{Q}}$

where:

• _i is the energy of the specific state, i, of interest
• k_B is Boltzmann's constant, which equals $1.3806\times 10^{-34}$ JK^-1
• T is the temperature in Kelvin

The denominator of this function is known as the partition function, Q, which corresponds to the total number of accessible states of the molecule.

The closed form of the molecular vibrational partition function is given by:

$q_{vib}={\frac {1}{1-e^{-h\nu /k_{B}T}}}$

where:

• $\nu$ is the fundamental vibrational frequency of N₂ in s^-1
• h is Planck's constant, which is $6.62607\times 10^{-34}$ Js

This is equivalent to Q since only the vibrational energy states are of interest and there is only one molecule of N₂. The equation for determining the partition function Q, from molecular partition functions, q, is given by:

$Q={\frac {q^{N}}{N!}}$

where:

• N is the number of molecules

The fundamental vibrational frequency of N₂ in wavenumbers, ${\tilde {\nu }}$, is 2358.6cm^-1

The fundamental vibrational frequency in s^-1 is given by:

$\nu ={\tilde {\nu }}\times c$

where

• c is the speed of light, which is $2.9979\times 10^{10}$ cm/s

For N₂,

$\nu$ = (2358.6cm^-1) \times (2.9979 \times 10^{10| cm/s) = 7.0708 \times 10^{13}</math>

For N₂ at 298 K,

$q_{v}=\left({\frac {1}{1-e^{-(6.62607\times 10^{-34}Js\times 7.0708\times 10^{13}s^{-1})/(1.3806\times 10^{-23}JK^{-1}\times 298K)}}}\right)=1.000011333$

The vibrational energy levels follow that of a quantum mechanical harmonic oscillator. The energy levels are represented by:

$E_{n}=h\nu (n+{\frac {1}{2}})$

where:

• n is the quantum vibrational number, which equals 0, 1, 2,...

For the ground state (n=0), the energy becomes:

$E_{0}={\frac {1}{2}}h\nu$

Since the vibrational zero point energy is not zero, the energy levels are defined relative to the n=0 level. This is used in the molecular partition function above and therefore, the ground state is regarded as having zero energy.

For N₂ the probability of being in the ground state at 298K is:

$P_{0}={\frac {e^{-E_{0}/k_{B}T}}{q_{v}}}$

$P_{0}={\frac {e^{(0J)/(1.3806\times 10^{-23}\times 298K)}}{1.000011333}}$

$P_{0}=0.999988667$

This means that at room temperature, the probability of a molecule of N₂ being in the ground vibrational state is 99.9988667%.

Problem 2

Derive an equation for the population of rotational state i of a linear diatomic. Make a bar graph of the distribution of rotational states of N₂ at 298 K.

1. Equation for the population of rotational state i

For a diatomic molecule, it can be approximated as a rigid rotor. Solving Schrödinger equation of rigid rotors gives the energy levels of the molecule at state J:

$E(J)=BJ(J+1)$

where $J$ is the quantum number for total rotational angular momentum; $B$ is the rotational constant in cm^-1.

• $B={\frac {h}{8\pi ^{2}cI}}$,

where $h$ is Planck constant; $c$ is the vacuum light speed in cm/s; and $I$ is the moment of inertia.

• $I=\mu r^{2}$,

where $\mu$ is the reduced mass and $r$ is the bond length.

By the Maxwell–Boltzmann_distribution, the population of rotational state i comparing to ground state is:

${\frac {N_{i}}{N_{0}}}={\frac {g_{i}}{g_{0}}}\left({\frac {e^{-E_{i}/k_{B}T}}{e^{-E_{0}/k_{B}T}}}\right)$

where $g$ is the degeneracy of the state; $E$ is the energy of the state; $k_{B}$ is Boltzmann constant and $T$ is the temperature.

Substitute $E_{i}=hcBi(i+1)$ ,$E_{0}=hcB0(0+1)=0$, and the degeneracy of the state i $g_{i}=2i+1$ to the equation, get:

${\frac {N_{i}}{N_{0}}}=(2i+1)\left({\frac {e^{-hcBi(i+1)/k_{B}T}}{e^{0/k_{B}T}}}\right)=(2i+1)e^{-hcBi(i+1)/k_{B}T}$

2. Distribution of rotational states of N₂

For N₂, the population of state i is:

${\frac {N_{i}}{N_{0}}}=(2i+1)e^{-hcBi(i+1)/k_{B}T}$

Combine the constant part, define constant $a=hcB/k_{B}T={\frac {h^{2}}{8\pi ^{2}k_{B}T\mu r^{2}}}$.

The reduced mass μ of Nitrogen is 7.00D a=1.16×10^-26 kg and the bond length r of N₂ is 110 pm = 1.10×10^-10m.

Substitute T = 298 K, $a={\frac {h^{2}}{8\pi ^{2}k_{B}T\mu r^{2}}}=9.60\times 10^{-3}$

By sum over states, q_rot=1/a = 104, so the probability of N₂ occupying the ground vibrational state at 298 K is 1/104 = 9.60×10^-3

The bar graph of the distribution of rotational states of N₂ at 298 K is:

Distribution of rotational states of nitrogen gas at 298 K.

Problem 3

Estimate the number of translational states that are available to a molecule of N₂ in 1 m³ container at 298 K.

The equation that is used to determine translational states of the molecule of N₂ at 298 K is shown below.

$q_{trans}(V,T)=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{\frac {3}{2}}$$V$

Where $q_{trans}$(V,T) represents the partition function for translation, $m$ represents the mass of the particle in kilograms (kg), $k_{B}$ represents Boltzmann's constant $(1.38064852\times 10^{-23}J\times K^{-1})$, $T$ represents the temperature in kelvins $(K)$, $h^{2}$ represents Planck's constant $(6.626\times 10^{-34}J\times s)$ and $V$ represents the volume in 3 dimensions in $m^{3}$.

The steps for solving this problem is shown below:

m = $28.0102$ amu

m = $(28.0102amu)(1.6605\times 10^{-27}kg)$

m = $4.6512\times 10^{-26}kg$

$q_{trans}(V,T)=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{3/2}V$

$q_{trans}(V,T)=\left({\frac {2\times 3.14159\times (4.6512\times 10^{-26}kg)\times (1.38064852\times 10^{-23}J/K)\times 298K}{{(6.626\times 10^{-34}J\times s})^{2}}}\right)^{3/2}(1.000m^{3})$

$q_{trans}(V,T)=1.4322\times 10^{32}$

Therefore, there should be $1.4322\times 10^{32}$ translational states for N₂ at 298 K.

Problem 4

Calculate the DeBroglie wavelength, rotational temperature, and vibrational temperature of N₂ and Cl₂ at 298 K.

The DeBroglie Wavelength

$\Lambda =\left({\frac {2{\pi }mk_{B}T}{h^{2}}}\right)^{-1/2}$

where:

• m is the mass of the molecule.
• Boltzmann's constant k_B = 1.3806488×10^-23 J K^-1
• Planck's constant h = 6.62606957×10^-34 J s

For N₂ at 298K,

$m=2\times 14.0067u$

$m=28.0134u\times {\frac {1.66054\times 10^{-27}kg}{u}}$

$m=4.65173712\times 10^{-26}kg$

$\Lambda =\left({\frac {2{\pi }(4.65173712\times 10^{-26}kg)(1.3806488\times 10^{-23}JK^{-1})(298K)}{(6.62606957\times 10^{-34}Js)^{2}}}\right)^{-1/2}$

$\Lambda =\left({\frac {1.20252611\times 10^{-45}kgJ}{4.39047979\times 10^{-67}J^{2}s^{2}}}\right)^{-1/2}$

$\Lambda =(2.738940097\times 10^{-21}kgJ^{-1}s^{-2})^{-1/2}$

$\Lambda =1.9107714\times 10^{-11}m$

For Cl₂ at 298K,

$m=2\times 35.453u$

$m=70.906u\times {\frac {1.66054\times 10^{-27}kg}{u}}$

$m=1.17742249\times 10^{-25}kg$

$\Lambda =\left({\frac {2{\pi }(1.17742249\times 10^{-25}kg)(1.3806488\times 10^{-23}JK^{-1})(298K)}{(6.62606957\times 10^{-34}Js)^{2}}}\right)^{-1/2}$

$\Lambda =\left({\frac {3.04376893\times 10^{-45}kgJ}{4.39047979\times 10^{-67}J^{2}s^{2}}}\right)^{-1/2}$

$\Lambda =(6.932656726\times 10^{21}kgJ^{-1}s^{-2})^{-1/2}$

$\Lambda =1.20101976\times 10^{-11}m$

Unit Conversion for the DeBroglie Wavelength:

$(kgJ^{-1}s^{-2})^{-1/2}=\left({\frac {kg}{kgm^{2}s^{-2}s^{2}}}\right)^{-1/2}$

$(kgJ^{-1}s^{-2})^{-1/2}=(m^{-2})^{-1/2}$

$(kgJ^{-1}s^{-2})^{-1/2}=m$

The Rotational Temperature

$\Theta _{r}={\frac {\hbar ^{2}}{2k_{B}\mu r_{e}^{2}}}$

where:

• Planck's constant $\hbar ={\frac {h}{2\pi }}={\frac {6.62606957\times 10^{-34}Js}{2\pi }}=1.054571726\times 10^{-34}Js$
• μ is the reduced mass.
• r_e is the bond length between two atoms in a molecule

For N₂,

r_e = 1.09769Å = 1.09769×10^-10m

$\mu ={\frac {m_{N}m_{N}}{m_{N}+m_{N}}}={\frac {m_{N}^{2}}{2m_{N}}}={\frac {m_{N}}{2}}={\frac {14.00307400529u}{2}}=7.001537003u$

$\mu =7.001537003u\times {\frac {1.66054\times 10^{-27}kg}{u}}$

$\mu =1.16263323\times 10^{-26}kg$

$\Theta _{r}={\frac {(1.054571726\times 10^{-34}Js)^{2}}{2(1.3806488\times 10^{-23}JK^{-1})(1.16263323\times 10^{-26}kg)(1.09769\times 10^{-10}m)^{2}}}$

$\Theta _{r}={\frac {1.11212153\times 10^{-68}J^{2}s^{2}}{3.86825738\times 10^{-69}JK^{-1}kgm^{2}}}$

$\Theta _{r}=2.874993624Js^{2}Kkg^{-1}m^{-2}$

$\Theta _{r}=2.874993624K$

For Cl₂,

r_e = 1.988Å = 1.988×10^-10m

$\mu ={\frac {m_{Cl}m_{Cl}}{m_{Cl}+m_{Cl}}}={\frac {m_{Cl}^{2}}{2m_{Cl}}}={\frac {m_{Cl}}{2}}={\frac {34.968852714u}{2}}=17.48442636u$

$\mu =17.4842636u\times {\frac {1.66054\times 10^{-27}kg}{u}}$

$\mu =2.90335893\times 10^{-26}kg$

$\Theta _{r}={\frac {(1.054571726\times 10^{-34}Js)^{2}}{2(1.3806488\times 10^{-23}JK^{-1})(2.90335893\times 10^{-26}kg)(1.988\times 10^{-10}m)^{2}}}$

$\Theta _{r}={\frac {1.11212153\times 10^{-68}J^{2}s^{2}}{3.16844888\times 10^{-68}JK^{-1}kgm^{2}}}$

$\Theta _{r}=0.350998729Js^{2}Kkg^{-1}m^{-2}$

$\Theta _{r}=0.350998729K$

Unit Conversion for the Rotational Temperature:

$Js^{2}Kkg^{-1}m^{-2}=J(kg^{-1}m^{-2}s^{2})K$

$Js^{2}Kkg^{-1}m^{-2}=JJ^{-1}K$

$Js^{2}Kkg^{-1}m^{-2}=K$

The Vibrational Temperature

$\Theta _{v}={\frac {h\nu }{k_{B}}}$

$\Theta _{v}={\frac {h{\tilde {\nu }}c}{k_{B}}}$

where:

• ${\tilde {\nu }}$ the vibrational frequency of the molecule in wavenumbers.
• The speed of light c = 2.99792458×10¹⁰cm s^-1

For N₂,

${\tilde {\nu }}=2358.57cm^{-1}$

$\Theta _{v}={\frac {(6.62606957\times 10^{-34}Js)(2358.57cm^{-1})(2.99792458\times 10^{10}cms^{-1})}{1.3806488\times 10^{-23}JK^{-1}}}$

$\Theta _{v}={\frac {4.6851712\times 10^{-20}J}{1.3806488\times 10^{-23}JK^{-1}}}$

$\Theta _{v}=3393.456175K$

For Cl₂,

${\tilde {\nu }}=559.7cm^{-1}$

$\Theta _{v}={\frac {(6.62606957\times 10^{-34}Js)(559.7cm^{-1})(2.99792458\times 10^{10}cms^{-1})}{1.3806488\times 10^{-23}JK^{-1}}}$

$\Theta _{v}={\frac {1.11181365\times 10^{-20}J}{1.3806488\times 10^{-23}JK^{-1}}}$

$\Theta _{v}=805.2834645K$

References

Molecule	N2	Cl2
$\Lambda$	1.91×10-11 m	1.20×10-11m
$\Theta _{r}$	2.87 K	0.351 K
$\Theta _{v}$	3.39×103 K	805 K

Problem 5

At what temperature would the probability for N₂ being the ground vibrational state be reduced to 50%?

50% of the N₂ molecules are in the ground state, and 50% are in the excited state. So, the population can be expressed in the following equation:

$P_{0}=0.5$

The value for the ${\tilde {\nu }}$ wavenumber value for the N₂ molecule, taken from the NIST Webbook, is 2358.57 cm^-1

This can be converted into the fundamental vibrational frequency by the relation,

$\nu ={\tilde {\nu }}\times c$

where:

• ${\tilde {\nu }}$ is fundamental wavenumber for the molecule in cm^-1.
• $c$ is the speed of light, 2.998x10¹⁰ cm/s By knowing this relation, the fundamental vibrational frequency can be calculated.

$\nu ={\tilde {\nu }}\times c=2358.57cm^{-1}\times 2.998\times 10^{10}cm/s=7.07099\times 10^{13}s^{-1}$

The population of a system can be expressed by the following equation:

$P_{0}={\frac {\exp \left({\frac {-E_{0}}{k_{B}T}}\right)}{q_{vib}}}$

where:

• $P_{0}$ is the population of the ground state molecules
• $E_{0}$ is the energy at the ground state
• $k_{B}$is the Boltzmann constant, 1.38064853 \times 10^-23 J/K
• $T$ is the temperature of the system in K
• $q_{vib}$ is the molecular vibrational partition function

$q_{vib}$ is related by the following equation:

$q_{vib}={\frac {1}{1-\exp \left({\frac {-h\nu }{k_{B}T}}\right)}}$

where:

• h is the Planck constant, 6.626*10^-34 J*s

Knowing these relations, we can solve for the temperature of the system when the molecule is reduced to 50% ground state, which is when 50% of the molecules are in the ground state and 50% of the molecules are excited.

$P_{0}={\frac {\exp {\frac {-E_{0}}{k_{B}T}}}{q_{vib}}}=50\%=0.5$

$q_{vib}={\frac {\exp \left({\frac {-E_{0}}{k_{B}T}}\right)}{P_{0}}}$

$q_{vib}={\frac {\exp(0)}{0.5}}=2$

Knowing the value of $q_{vib}$, we can solve the molecular vibrational partition function to obtain the exact value of T for when 50% of the molecules are in the ground state.

$q_{vib}={\frac {1}{1-e^{\frac {-h\nu }{k_{B}T}}}}$$=2$

$2={\frac {1}{1-\exp ^{\frac {-h\nu }{k_{B}T}}}}$

$2(1-\exp ^{\frac {-h\nu }{k_{B}T}})=1$

$2-2\exp ^{\frac {-h\nu }{k_{B}T}}=1$

$-2\exp \left({\frac {-h\nu }{k_{B}T}}\right)=-1$

$\exp \left({\frac {-h\nu }{k_{B}T}}\right)=0.5$

$\ln(\exp \left({\frac {-h\nu }{k_{B}T}}\right)=\ln(0.5)$

${\frac {-h\nu }{k_{B}T}}=-0.6931472$

$T={\frac {h\nu }{0.6931472k_{B}}}$

Therefore, by substituting the Planck constant, fundamental vibrational frequency and the Boltzmann constant into the equation, we can obtain the temperature for when half of the molecules are in the ground state.

$T=6.626\times 10^{-34}J\cdot s\times 7.07099\times 10^{13}s^{-}1/(0.6931472\times 1.38064853\times 10^{-23}J/K)=4895.792994K$

The temperature at which 50% of the N₂ molecules are in the ground vibrational state is 4895 K.

Variables of the Canonical Ensemble

The Canonical Ensemble partition function depends on variables including the composition (N), volume (V) and temperature (T) of a given system, where the above partition function equation is still valid with $Q_{N,V,T}=Q(N,V,T)$.

The partition function of the canonical ensemble is defined as the sum over all states of a particular system involving each states respective energies, and represented by the following equation,

$Q=\sum _{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)$

In this equation, $k_{B}$ represents the Boltzmann Constant with a value of $k_{B}=1.3806503\times 10^{-23}JK^{-1}$, T represents the temperature in kelvin and $E_{j}$ is the energy at state j.

Internal Energy

The partition function can also be related to all state functions from classical thermodynamics, such as U, A, G and S. The ensemble average of the internal energy in a given system is the thermodynamic equivalent to internal energy, as stated by the Gibbs postulate, and defined by,

$U=\langle E\rangle ={\frac {\sum _{j}E_{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)}{Q}}$

Where the variable Q here represents the partition function term. For a canonical ensemble, the internal energy can be derived from the above equation by considering the derivative of Q with respect to T,

${\begin{alignedat}{7}{\frac {\partial {}}{\partial {T}}}Q={\frac {\partial {}}{\partial {T}}}\sum _{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)&\\=\sum _{j}{\frac {\partial {}}{\partial {T}}}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)&\\=\sum _{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right){\frac {\partial {}}{\partial {T}}}\left({\frac {-E_{j}}{k_{B}T}}\right)&\\={\frac {E_{j}}{k_{B}}}{\frac {1}{T^{2}}}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)&\\\end{alignedat}}$

${\begin{alignedat}{7}{\frac {\partial {}}{\partial {T}}}Q=\sum _{j}{\frac {E_{j}}{k_{B}}}{\frac {1}{T^{2}}}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)={\frac {1}{k_{B}T^{2}}}\sum _{j}E_{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)&\\={\frac {Q}{Q}}{\frac {1}{k_{B}T^{2}}}\sum _{j}E_{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)&\\=Q{\frac {1}{k_{B}T^{2}}}{\frac {\sum _{j}E_{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)}{Q}}&\\={\frac {Q}{k_{B}T^{2}}}{\frac {\sum _{j}E_{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)}{Q}}={\frac {Q}{k_{B}T^{2}}}\langle E\rangle \end{alignedat}}$

Rearranging this resulting equation for $\langle E\rangle$ yields,

$\langle E\rangle =k_{B}T^{2}{\frac {1}{Q}}\left({\frac {\partial {Q}}{\partial {T}}}\right)_{N,V}$

and from the Gibbs Postulate,

$U=k_{B}T^{2}\left({\frac {\partial {\textrm {ln}}Q}{\partial T}}\right)_{N,V}$

Helmholtz Energy

The Helmholtz Energy, or Helmholtz Free Energy, of a Canonical Ensemble represents the amount of work and energy obtainable by a certain closed system under constant concentration, volume and temperature. The expression for A utilizes both the internal energy and entropy of the system, and is derived by,

$A=U-TS$

Where A is the Helmholtz Energy term, U represents the internal energy and S represents the entropy of the system being studied. Substituting the per-determined values for the canonical ensemble,

$A=\langle E\rangle -T\left({\frac {\langle E\rangle }{T}}+k_{B}\ln {Q}\right)$

$A=\langle E\rangle -\langle E\rangle -k_{B}T\ln {Q}$

$A=-k_{B}T\ln \left(Q\right)$

Q represents the partition function for this particular system, and is proportional to the absolute free energy. Thus, an increase in $\ln(Q)$ will occur with an increase in the number of total accessible states, and a more negative free energy.

Entropy

The Gibbs definition of Entropy is described by,

$S=-k_{B}\sum _{j}P_{j}\ln {P_{j}}$

where $P_{j}$ represents the Probability of being in state i and described by the weight of the state divided by the sum of all possible weights, such as,

$P_{i}={\frac {\exp \left({\frac {-E_{i}}{k_{B}T}}\right)}{\sum _{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)}}$

and thus large probabilities of multiple states correlate with large values of S. By using the above Gibbs definition, the entropy of a Canonical Ensemble (NVT) can be derived, in terms of Q, to yield the following expression,

$S={\frac {\langle E\rangle }{T}}+k_{B}\ln {Q}$ or $S=k_{B}T\left({\frac {\partial {\ln {Q}}}{\partial {T}}}\right)_{N,V}+k_{B}\ln {Q}$

The value of Q in this equation can also be represented as $Q={\frac {q^{n}}{N!}}$, where q is equivalent to the partition function of the molecules, with N representing the number of molecules, in the system.

The partition function is also represented by the denominator of the probability term for a certain state, given by the following,

$P_{i}={\frac {\exp \left({\frac {-E_{j}}{k_{B}T}}\right)}{Q}}$

Chemical potential

The Chemical Potential, μ, represents the change in the Helmholtz free energy when an additional particle is added to the canonical ensemble system. A heterogeneous system represents a system containing more than one type of gas and the expression for the chemical potential here is μi, where i represents each differing species. This term is derived from Helmholtz free energy, A, with respect to number of molecules for a certain species i. Thus,

$\mu _{i}=\left({\frac {\partial {A}}{\partial {N_{i}}}}\right)_{T,V,N}$

And utilizing the above Helmholtz expression, the following can be derived,

$=\left({\frac {\partial {}-k_{B}T\ln {Q}}{\partial {N_{i}}}}\right)_{T,V,N}$

$=-k_{B}T\left({\frac {\partial {\ln {\frac {q_{i}\left(V,T\right)^{N_{i}}}{N_{i}!}}}}{\partial {N_{i}}}}\right)_{T,V,N}$

$=-k_{B}T\left({\frac {\partial {\ln {q_{i}\left(V,T\right)^{N_{i}}}}-\ln {N_{i}!}}{\partial {N_{i}}}}\right)_{T,V,N}$

$=-k_{B}T\left({\frac {\partial {N_{i}\ln {q_{i}\left(V,T\right)}}-N_{i}\ln {N_{i}}+N_{i}}{\partial {N_{i}}}}\right)_{T,V,N}$

$=-k_{B}T\left(\ln {q_{i}}\left(V,T\right)-\ln {N_{i}}-1+1\right)_{T,V,N}$

$\mu =-k_{B}T\ln {}\left({\frac {q_{i}\left(V,T\right)}{N_{i}}}\right)$

This definition helps describe the change in the Helmholtz free energy with a changing system composition, such as a reaction forming and/or consuming certain molecules in a system.

Heat Capacity

In this section, we will complete the deviation of heat capacity in terms of the partition function Q.

$Q={\displaystyle \sum _{j}\exp(-E_{j}/k_{B}T)}$

According to the Gibbs postulate, the ensemble average is equal to the average internal energy, U

$U=\langle E\rangle ={\frac {\displaystyle \sum _{j}E_{j}\exp(-E_{j}/k_{B}T)}{Q}}$

Substitute equation for partition function into ensemble average.

$\langle E\rangle ={\frac {\displaystyle \sum _{j}E_{j}\exp(-E_{j}/k_{B}T)}{\displaystyle \sum _{j}\exp(-E_{j}/k_{B}T)}}$

$\beta ={\frac {1}{k_{B}T}}$ , which is the Boltzmann's Constant.

Now substituting $\beta$ you get,

$\langle E\rangle ={\frac {\displaystyle \sum _{j}E_{j}\exp(-\beta E_{j})}{\displaystyle \sum _{j}\exp(-\beta E_{j})}}$

$C_{v}=\left({\frac {d\langle E\rangle }{dT}}\right)$, which is the heat capacity.

To find the equation of heat capacity using Statistical Mechanics we first have to differentiate the ensemble average with respect to $\beta$.

$\left({\frac {d\langle E\rangle }{dT}}\right)_{N,V}={\frac {\displaystyle \sum _{j}E_{j}\exp(-\beta E_{j})}{\displaystyle \sum _{j}\exp(-\beta E_{j})}}$ $={\frac {-1}{Q}}\left({\frac {dQ}{d\beta }}\right)_{N,V}$

Therefore, the equation of heat capacity with respect to the partition function Q is,

$C_{v}={\frac {-1}{Q}}\left({\frac {dQ}{d\beta }}\right)_{N,V}$

Chemical Equilibrium

Chemical Equilibrium from Statistical Thermodynamics

Consider the general gas phase chemical reaction represented by

${\ce {\nu_{A}A + \nu_{B}B <=>\nu_{C}C + \nu_{D}D}}$

where A, B, C and D are the reactants and products of the reaction, and $\nu _{A}$ is the stoichiometric coefficient of chemical A, $\nu _{B}$ is the stoichiometric coefficient of chemical B, and so on. Each of the gases involved in the reaction will eventually reach an equilibrium concentration when the forward and reverse reaction rates become equal. The distribution of reactants to products at the quilibrium point is represented by the equilibrium constant ($K_{c}$):

$K_{c}={\frac {[C]^{\nu _{C}}[D]^{\nu _{D}}}{[A]^{\nu _{A}}[B]^{\nu _{B}}}}={\frac {\rho _{C}^{\nu _{C}}\rho _{D}^{\nu _{D}}}{\rho _{A}^{\nu _{A}}\rho _{B}^{\nu _{B}}}}$

If the system is not at equilibrium, a shift in the number of reactants and products will occur to lower the overall energy of the system. The difference in the energy of the system at this non-equilibrated point and the energy of the system at equilibrium for any particular species is termed chemical potential. When both temperature and volume are constant for both points aforementioned, the chemical potential $\mu$ of species i is expressed by the equation

$\mu _{i}={\left({\frac {\partial A}{\partial N_{i}}}\right)}_{T,V,N_{j\neq 1}}$

where A is the Helmholtz energy, and $N_{i}$ is the number of molecules of species i. The Helmholtz energy can be determined as a function of the total partition function, Q:

$A=-k_{B}T\ln Q$

where $k_{B}$ is the Boltzmann constant and T is the temperature of the system. The total partition function is given by

$Q={\frac {q_{i}(V,T)^{Ni}}{N_{i}!}}$

where $q_{i}$ is the molecular partition function of chemical species i. Substituting the molecular partition funCtion into the equation for helholtz energy yields:

$A=-k_{B}T\ln \left({\frac {q_{i}(V,T)^{Ni}}{N_{i}!}}\right)$

and then further substituting this equation into the definition of chemical potential yields:

$\mu _{i}={\left({\frac {\partial -k_{B}T\ln \left({\frac {q_{i}(V,T)^{Ni}}{N_{i}!}}\right)}{\partial N_{i}}}\right)}_{T,V,N_{j\neq 1}}$

rearranging this equation the following derivative can be set-up:

$\mu _{i}=-k_{B}T{\left({\left({\frac {\partial {Ni}\ln \left({q_{i}(V,T)}\right)}{\partial N_{i}}}\right)}-{\left({\frac {\partial \ln \left({N_{i}!}\right)}{\partial N_{i}}}\right)}\right)}_{T,V,N_{j\neq 1}}$

From this point Sterling's approximation

$\ln {N!}=N\ln N-N$

can be substituted into the derivative to yield:

$\mu _{i}=-k_{B}T{\left({\left({\frac {\partial {Ni}\ln \left({q_{i}(V,T)}\right)}{\partial N_{i}}}\right)}-{\left({\frac {\partial \left({N_{i}\ln N_{i}-N_{i}}\right)}{\partial N_{i}}}\right)}\right)}_{T,V,N_{j\neq 1}}$

From here the derivative can be rearranged and solved:

$\mu _{i}=-k_{B}T{\left({\ln \left({q_{i}(V,T)}\right)}{\frac {\partial {N_{i}}}{\partial N_{i}}}+{{N_{i}}{\frac {\partial \ln \left({q_{i}(V,T)}\right)}{\partial N_{i}}}}-{\ln \left({N_{i}}\right){\frac {\partial {N_{i}}}{\partial N_{i}}}}-{{N_{i}}{\frac {\partial \ln \left({N_{i}}\right)}{\partial N_{i}}}}+{\frac {\partial {N_{i}}}{\partial N_{i}}}\right)}_{T,V,N_{j\neq 1}}$

$\mu _{i}=-k_{B}T{\left({\ln {\left({q_{i}(V,T)}\right)}}+{0}-{\ln \left({N_{i}}\right)}-{N_{i}{\frac {1}{N_{i}}}}+{1}\right)}$

$\mu _{i}=-k_{B}T{\left({\ln {\left({q_{i}(V,T)}\right)}}-{\ln \left({N_{i}}\right)}\right)}$

$\mu _{i}=-k_{B}T\ln \left({\frac {q_{i}(V,T)}{N_{i}}}\right)$

A variable, $\lambda$, is then defined such that $dN_{j}=\nu _{j}d\lambda$, where j = A, B, C or D and $\nu _{j}$ is taken to be positive for products and negative for reactants. A change in $\lambda$ therefore corresponds to a change in the concentrations of the reactants and products. Thus, at equilibrium,

$\left({\frac {\partial A}{\partial \lambda }}\right)_{T,V}=0$

Helmholtz Energy with respect to Equilibrium Shifts

From Classical thermodynamics, the total differential of A is:

$dA=-SdT-pdV+\sum _{j}\mu _{j}dN_{j}$

For a reaction at a fixed volume and temperature (such as in the canonical ensemble), $dT$ and $dV$ equal 0. Therefore,

$dA=\sum _{j}\mu _{j}dN_{j}$

$dA=\sum _{j}\mu _{j}\nu _{j}d\lambda$

$dA=d\lambda \sum _{j}\mu _{j}\nu _{j}$

$\sum _{j}\mu _{j}\nu _{j}=0$

Substituting the expanded form of chemical potential:

$-k_{B}T\sum _{j}\ln \left({\frac {q_{i}}{N_{i}}}\right)\nu _{j}=0$

$\sum _{j}\ln \left({\frac {q_{i}}{N_{i}}}\right)\nu _{j}=0$

$\sum _{j}\nu _{j}[\ln(q_{j})-\ln(N_{j})]=0$

For the reaction ${\ce {\nu_{a}A + \nu_{b}B <=>\nu_{c}C + \nu_{d}D}}$:

$[\nu _{C}\ln(q_{C})-\nu _{C}\ln(N_{C})]+[\nu _{D}\ln(q_{D})-\nu _{D}\ln(N_{D})]-[\nu _{A}\ln(q_{A})-\nu _{A}\ln(N_{A})]-[\nu _{B}\ln(q_{B})-\nu _{B}\ln(N_{B})]=0$

This equation simplifies to

${\frac {(q_{C})^{\nu _{C}}(q_{D})^{\nu _{D}}}{(q_{A})^{\nu _{A}}(q_{B})^{\nu _{B}}}}={\frac {(N_{C})^{\nu _{C}}(N_{D})^{\nu _{D}}}{(N_{A})^{\nu _{A}}(N_{B})^{\nu _{B}}}}$

By dividing all terms by volume, and noting the relationship ${\frac {N_{A}}{V}}={\frac {\#molecules}{volume}}=\rho _{A}=[A]$ where $\rho$ is referred to a number density, the following equation is obtained:

$K_{c}={\frac {\rho _{C}^{\nu _{C}}\rho _{D}^{\nu _{D}}}{\rho _{A}^{\nu _{A}}\rho _{B}^{\nu _{B}}}}={\frac {(q_{C}/V)^{\nu _{C}}(q_{D}/V)^{\nu _{D}}}{(q_{A}/V)^{\nu _{A}}(q_{B}/V)^{\nu _{B}}}}$

Partition Functions

The molecular partition function, $q_{i}$ is defined as the product of the translational, rotational, vibration and electronic partition functions:

$q=q_{trans}q_{rot}q_{vib}q_{elec}$

These components of the molecular partition function may be defined as follows:

$q_{trans}=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{3/2}V$

where m is the mass of a single particle and h is Planck's constant, and T is temperature.

$q_{rot}={\frac {2k_{B}T\mu {r_{e}}^{2}}{\sigma \hbar ^{2}}}$

where $\mu$ is the reduced mass of the molecule, $r_{e}$ is the bond length between the atoms in the molecule, and $\hbar$ is the reduced Planck's constant.

$q_{vib}={\frac {1}{1-\exp \left({\frac {-h\nu }{k_{B}T}}\right)}}$

where $\nu$ is the vibrational frequency of the molecule.

$q_{elec}=g_{1}e^{D_{0}/k_{b}T}$

where $g_{1}$ is the degeneracy of the ground state, and $D_{0}$ is the bond energy of the molecule.

Thus, the equilibrium constant of a chemical reaction can be expressed in terms of the molecular partition functions and the difference in atomization energies of the products and reactants $\Delta D_{0}$.

$K_{eq}={\frac {\prod _{i}^{products}\left(q_{i}/V\right)^{v_{i}}}{\prod _{i}^{reactants}\left(q_{i}/V\right)^{v_{i}}}}\exp \left({\frac {\Delta D_{0}}{k_{B}T}}\right)$

$\Delta D_{0}=\sum _{products}^{i}D_{0,i}-\sum _{reactants}^{i}D_{0,i}$

Example

Calculate the equilibrium constant for the reaction of ${\ce {H2 (g)}}$ and ${\ce {Cl2 (g)}}$ at 650 K.

${\ce {H2 (g) + Cl2 (g) <=> 2HCl (g)}}$

Equilibrium Constant Equation (From Molecular Partition Functions) $K_{c}(T)={\left({\frac {{\Bigl (}{\frac {q_{\text{HCl}}}{V}}{\Bigr )}^{2}}{{\Bigl (}{\frac {q_{{\text{H}}_{2}}}{V}}{\Bigr )}{\Bigl (}{\frac {q_{{\text{Cl}}_{2}}}{V}}{\Bigr )}}}\right)}$

$K_{c}(T)={\left({\frac {{\Bigl (}{\frac {q_{trans{\text{HCl}}}q_{rot{\text{HCl}}}q_{vib{\text{HCl}}}q_{elec{\text{HCl}}}}{V}}{\Bigr )}^{2}}{{\Bigl (}{\frac {q_{trans{\text{H}}_{2}}q_{rot{\text{H}}_{2}}q_{vib{\text{H}}_{2}}q_{elec{\text{H}}_{2}}}{V}}{\Bigr )}({\frac {q_{trans{\text{Cl}}_{2}}q_{rot{\text{Cl}}_{2}}q_{vib{\text{Cl}}_{2}}q_{elec{\text{Cl}}_{2}}}{V}}{\Bigr )}}}\right)}$
A simple problem solving strategy for finding equilibrium constants via statistical mechanics is to separate the equation into the molecular partition functions of each of the reactant and product species, solve for each one, and recombine them to arrive at a final answer.

$\left({\frac {q_{\text{HCl}}}{V}}\right)=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{3/2}\times {\frac {2k_{B}T\mu r_{e}^{2}}{\sigma \hbar ^{2}}}\times {\frac {1}{1-\exp {{\Bigl (}{\frac {-h\nu }{k_{B}T}}{\Bigr )}}}}\times g_{1}\exp(D_{0}/K_{B}T)$

In order to simplify the calculations of molecular partition functions, the characteristic temperature of rotation ($\Theta _{r}$) and vibration ($\Theta _{\nu }$) are used. These values are constants that incorporate the physical constants found in the rotational and vibrational partition functions of the molecules. Tabulated values of $\Theta _{r}$ and $\Theta _{\nu }$ for select molecules can be found here.

Species	$\Theta _{\nu }$ (K)	$\Theta _{r}$ (K)	$D_{0}$ (kJ mol-1)
${\ce {Cl2 (g)}}$	6125	0.351	239.0
${\ce {H2 (g)}}$	808	87.6	431.9
${\ce {HCl (g)}}$	4303	15.2	427.7

$\left({\frac {q_{\text{HCl}}}{V}}\right)=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{3/2}\times {\frac {T}{\sigma \Theta _{r}}}\times {\frac {1}{1-\exp {{\Bigl (}{\frac {-\Theta _{\nu }}{T}}{\Bigr )}}}}\times g_{1}\exp(D_{0}/RT)$ $\left({\frac {q_{\text{HCl}}}{V}}\right)=\left({\frac {2\pi (2.1957\times 10^{-24}{\text{kg}})(1.38065\times 10^{-23}{\text{JK}}^{-1})(650K)}{(6.62607\times 10^{-34}{\text{Js}})^{2}}}\right)^{3/2}\times {\frac {650{\text{K}}}{(2)(15.2{\text{K}})}}\times {\frac {1}{1-\exp {{\Bigl (}{\frac {-4303{\text{K}}}{650{\text{K}}}}{\Bigr )}}}}\times (1)\exp((427700{\text{Jmol}}^{-1})/(8.3145{\text{JKmol}}^{-1})(650{\text{K}}))$ $\left({\frac {q_{\text{HCl}}}{V}}\right)=(1.4975\times 10^{35}{\text{m}}^{-3})(21.4)(1.0013)(2.3419\times 10^{34})$

$\left({\frac {q_{{\text{H}}_{2}}}{V}}\right)=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{3/2}\times {\frac {T}{\sigma \Theta _{r}}}\times {\frac {1}{1-\exp {{\Bigl (}{\frac {-\Theta _{\nu }}{T}}{\Bigr )}}}}\times g_{1}\exp(D_{0}/RT)$ $\left({\frac {q_{{\text{H}}_{2}}}{V}}\right)=\left({\frac {2\pi (1.2140\times 10^{-25}{\text{kg}})(1.38065\times 10^{-23}{\text{JK}}^{-1})(650K)}{(6.62607\times 10^{-34}{\text{Js}})^{2}}}\right)^{3/2}\times {\frac {650{\text{K}}}{(2)(87.6{\text{K}})}}\times {\frac {1}{1-\exp {{\Bigl (}{\frac {-808{\text{K}}}{650{\text{K}}}}{\Bigr )}}}}\times (1)\exp((431900{\text{Jmol}}^{-1})/(8.3145{\text{JKmol}}^{-1})(650{\text{K}}))$ $\left({\frac {q_{{\text{H}}_{2}}}{V}}\right)=(1.9468\times 10^{33}{\text{m}}^{-3})(3.71)(1.41)(5.0942\times 10^{34})$

$\left({\frac {q_{{\text{Cl}}_{2}}}{V}}\right)=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{3/2}\times {\frac {T}{\sigma \Theta _{r}}}\times {\frac {1}{1-\exp {{\Bigl (}{\frac {-\Theta _{\nu }}{T}}{\Bigr )}}}}\times g_{1}\exp(D_{0}/RT)$ $\left({\frac {q_{{\text{Cl}}_{2}}}{V}}\right)=\left({\frac {2\pi (4.2700\times 10^{-24}{\text{kg}})(1.38065\times 10^{-23}{\text{JK}}^{-1})(650K)}{(6.62607\times 10^{-34}{\text{Js}})^{2}}}\right)^{3/2}\times {\frac {650{\text{K}}}{(2)(0.351{\text{K}})}}\times {\frac {1}{1-\exp {{\Bigl (}{\frac {-6125{\text{K}}}{650{\text{K}}}}{\Bigr )}}}}\times (1)\exp((239000{\text{Jmol}}^{-1})/(8.3145{\text{JKmol}}^{-1})(650{\text{K}}))$ $\left({\frac {q_{{\text{Cl}}_{2}}}{V}}\right)=(5.4839\times 10^{35}{\text{m}}^{-3})(925.9)(1.00)(1.606\times 10^{19})$

Combining the terms from each species, the following expression is obtained:

$K_{c}={\frac {(1.9468\times 10^{33}{\text{m}}^{-3})^{2}}{(1.9468\times 10^{33}{\text{m}}^{-3})(5.4839\times 10^{35}{\text{m}}^{-3})}}\times {\frac {(21.4)^{2}}{(3.71)(925.9)}}\times {\frac {(1.0013)^{2}}{(1.41)(1.00)}}\times {\frac {(2.3419\times 10^{34})^{2}}{(1.606\times 10^{19})(5.0942\times 10^{34})}}$ $K_{c}=(0.003550)(0.1333)(0.711)(6.7037\times 10^{14})$ $K_{c}=(2.26\times 10^{11})$

At 650 K, the reaction between ${\ce {H2 (g)}}$ and ${\ce {Cl2 (g)}}$ proceeds spontaneously towards the products. From a statistical mechanics point of view, the product ${\ce {HCl (g)}}$ molecule has more states accessible to it than the reactant species. The spontaneity of this reaction is largely due to the electronic partition function: two very strong H—Cl bonds are formed at the expense of a very strong H—H bond and a relatively weak Cl—Cl bond.

Eyring Transition State Theory

Figure 1: Reaction coordinate diagram for the bimolecular nucleophilic substitution (S_N2) reaction between bromomethane and the hydroxide anion

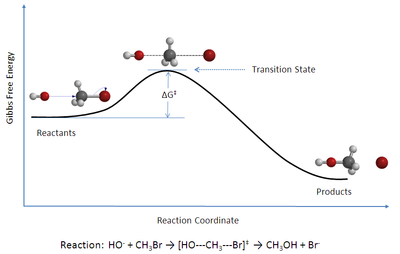
Chemical kinetics describes the rates of change of the concentration of species through chemical reactions.

Rate=$k[A]^{v_{a}}[B]^{v_{b}}$

The rate constant, k, is depends on the chemical species undergoing reaction and the reaction conditions (i.e, temperature).

Rate constants of elementary gas phase chemical reactions can be estimated by statistical thermodynamics using a rate theory. One of the simplest and more widely used theories is Eyring conventional transition state theory.

In Eyring conventional transition state theory, the rate constant of a chemical reaction can be expressed in terms of the partition functions of the transition state and the reactants. $\Delta E^{\ddagger }$ is the barrier height of the reaction.

$k={\frac {k_{B}T}{h}}{\frac {q_{TS}/V}{\prod _{i}^{reactants}\left(q_{i}/V\right)^{v_{i}}}}{\textrm {exp}}\left({\frac {-\Delta E^{\ddagger }}{k_{B}T}}\right)$

Assumptions of Transition State Theory

Transition state theory relies on three key assumptions in its derivation.

1. Reactants are in constant equilibrium with the transition state structure.
2. The energy of the particles follow a Boltzmann distribution.
3. Once reactants become the transition state, the transition state structure does not collapse back to the reactants.

Given a reaction where reactants A and B are converted to a transition state C:

${\ce {A+B<=>{}[C]^{\ddagger }}}$

The equilibrium constant, K^‡, can be written in terms of the concentrations of the reactants and the transition state.

$K^{\ddagger }={\frac {\ce {[C]^{\ddagger }}}{\ce {[A][B]}}}$

This reaction exists as an equilibrium because we assume that not every collision results in the formation of the transition state. Rewriting the concentrations in terms of the partition functions yields the equation below.

$k={\frac {k_{B}T}{h}}{\frac {q_{TS}/V}{\prod _{i}^{reactants}\left(q_{i}/V\right)^{v_{i}}}}{\textrm {exp}}\left({\frac {-\Delta E^{\ddagger }}{k_{B}T}}\right)$

Thermodynamic Representation of Eyring Equation

The Eyring equation can also be expressed in terms thermodynamic parameters. The standard free energy, ΔG^‡, can be written in terms of the equilibrium constant.

$\Delta G^{\ddagger }=-RT\ln(K^{\ddagger })$

$K^{\ddagger }=e^{\frac {-\Delta G^{\ddagger }}{RT}}$

Using the equation for standard Gibb's energy, the Eyring equation can be written as:

$k={\frac {k_{B}T}{h}}e^{\frac {-(\Delta H^{\ddagger }-T\Delta S^{\ddagger })}{RT}}$

Here, $\Delta H^{\ddagger }$is the enthalpy of activation and represents the enthalpy or energetic stability of the transition state structure; it is the energy needed to break the bonds of the reactants and form the transition state. Similar to standard enthalpy, a negative value represents a more stable energetic structure and vice versa. $\Delta S^{\ddagger }$is the entropy of activation, which represents the entropy, or disorder of the transition state and is the number of accessible states of transition state compared to the reactants. Likewise, a positive entropy represents a more disordered system while a negative entropy corresponds to a more ordered system.

Using the thermodynamical representation of the Eyring equation allows for the prediction of the type of mechanism a reaction can take. An associative mechanism involves a molecule bonding to another to form the transition state, while a dissociative mechanism involves the breaking of a molecule to form the transition state. In general, an associative mechanism occurs when the entropy of the transition state is lower than the reactants and thus the transition state is more ordered; this means change in entropy is negative. the result of this is that the entropy is lower and the structure is more ordered and has less accessible states. Contrary, a dissociative mechanism occurs when the entropy of the transition state is positive or higher for the transition state relative to the reactants. Thus, the transition state is less ordered than the initial reactants.

Partition functions of the transition state

TST requires the calculation of the partition functions for the transition state structure.

$q_{TS}=q_{trans,TS}\times q_{rot,TS}\times q_{vib,TS}^{'}\times q_{el,TS}$

The translational and rotational partition functions of the transition state have the same form as those used for the reactant species. The vibrational partition function differs slightly because the vibration that corresponds to crossing the barrier is removed from this term (it "becomes" the $k_{B}T/h$ term. As result, there is one fewer term in the vibrational partition function. For non-linear transition states, there will be $3N_{atom}-5$ terms. For linear transition states, there will be $3N_{atom}-4$ terms.

$q_{vib,TS}^{'}=\prod _{i}^{n_{vib}-1}{\frac {1}{1-\exp \left({\frac {-h{\nu }}{k_{B}T}}\right)}}$

Calculation of a rate constant using this theory requires that all the structural and mechanical properties of the transition state be known. This is a challenge because it is very difficult to use spectroscopy to determine the structural properties of a transition state, which typically only exists for 10-200 fs. Instead, computational chemistry is commonly used to calculate the properties of transition states.

Example

Calculate the rate constant for the reaction of H + H₂ at 300 K.

H + H₂ → H₂ + H

To calculate the rate constant the following are required, for both the reactants and the transition state:

• the masses of isotopes
• vibrational frequencies (q_vib)
• moments of inertia (q_rot)
• electronic degeneracies'
• reaction barrier height

Species	Vibration	$\nu$(cm-1)
H2	H-H stretch	4401.1272
H-H-H‡	H-H-H bend (degeneracy of 2)	875.62
H-H-H‡	H-H-H symmetric stretch	2050.67

R = 0.743 Å for the reactant R = 0.931 Å for the transition state $\Delta E$^‡ = 38.61 kJ mol^-1

translational partition functions:

$q_{trans}(V,T)=\left({\frac {2\pi k_{B}Tm}{h^{2}}}\right)^{3/2}$

for H₂: $q_{trans}(V,T)=\left({\frac {2\pi (1.381\times 10^{-23}JK^{-1})(300K)(2\times 1.6735575\times 10^{-27}kg)}{(6.626\times 10^{-34}Js)^{2}}}\right)^{3/2}$ $q_{trans}(V,T)=2.795\times 10^{29}m^{-3}$

For H-H-H:$q_{trans}(V,T)=\left({\frac {2\pi (1.381\times 10^{-23}JK^{-1})(300K)(3\times 1.6735575\times 10^{-27}kg)}{(6.626\times 10^{-34}Js)^{2}}}\right)^{3/2}$ $q_{trans}(V,T)=5.135\times 10^{30}m^{-3}$

rotational partition functions:

for H₂ : $q_{rot}(T)=\left({\frac {2k_{B}T\mu r_{e}^{2}}{\sigma \hbar ^{2}}}\right)$

         $q_{rot}(T)=\left({\frac {(2)(1.381\times 10^{-23}JK^{-1})(300K)(0.5)(1.674\times 10^{-27}kg)(7.43\times 10^{-11}m)^{2}}{2(1.058\times 10^{-34}Js)^{2}}}\right)$
         $q_{rot}(T)=1.71$

For H-H-H: $q_{rot}(T)=\left({\frac {2k_{B}T(2m_{A}R^{2})}{\sigma \hbar ^{2}}}\right)$

          $q_{rot}(T)=\left({\frac {2(1.381\times 10^{-27}JK^{-1}(300K)(2)(1.674\times 10^{-27}kg)(9.31\times 10^{-11}m)^{2}}{2(1.058\times 10^{-34}Js)^{2}}}\right)$
          $q_{rot}(T)=10.7$

vibrational partition functions:

for H₂:$q_{vib}(T)=\left({\frac {1}{1-\exp {\frac {-hc\nu _{1}}{k_{b}T}}}}\right)\left({\frac {1}{1-\exp {\frac {-hc\nu _{2}}{k_{B}T}}}}\right)\left({\frac {1}{1-\exp {\frac {-hc\nu _{3}}{k_{B}T}}}}\right)$

                  $q_{vib}(T)=\left({\frac {1}{1-\exp {\frac {-hc(875.62cm^{-1})}{k_{B}T}}}}\right)\left({\frac {1}{1-\exp {\frac {-hc(875.62cm^{-1})}{k_{B}T}}}}\right)\left({\frac {1}{1-\exp {\frac {-hc(2043.95cm^{-1})}{k_{B}T}}}}\right)$
                  $q_{vib}(T)=(1.015)(1.015)(1.000)$
                  $q_{vib}(T)=1.030$

Rate constant k:

$k=\left({\frac {k_{B}T}{h}}\right)\left({\frac {q_{trans,TS}/V}{(q_{trans,H}/V)(q_{trans,H_{2}}/V)}}\right)\left({\frac {q_{rot,TS}}{q_{rot,H_{2}}/V}}\right)\left({\frac {q'_{vib,H_{2}}}{q_{vib,H_{2}}}}\right)\left({\frac {g_{TS}}{g_{H}g_{H_{2}}}}\right)e^{-\Delta E^{\ddagger }/k_{B}T}$

$k=\left({\frac {(1.381\times 10^{-23}JK^{-1})(300K)}{6.626\times 10^{-34}Js}}\right)\left({\frac {5.135\times 10^{30}m^{-3}}{(9.883\times 10^{29}m^{-3})(2.795\times 10^{30}m^{-3})}}\right)\left({\frac {10.7}{1.71}}\right)\left({\frac {1.030}{1.00}}\right)\left({\frac {2}{2\times 1}}\right)e^{-38610Jmol^{-1}/6.022\times 10^{23}mol^{-1}/1.307\times 10^{-23}JK^{-1}\times 300K}$ $k=(6.251\times 10^{12}s^{-1})(1.8588\times 10^{-30}m^{3})(6.25)(1.03)(1)(1.894\times 10^{-7})$

$k=1.42\times 10^{-23}m^{3}s^{-1}$

Links

w:Transition state theory

References

Atkins, P., de Paula, J., Elements of Physical Chemistry, 5th ed.; Oxford University Press, 2009.

Blackbody Radiation

Blackbody radiation is the phenomenon where a heated object will emit electromagnetic radiation

As the temperature decreases, the peak of the black-body radiation curve moves to lower intensities and longer wavelengths. The black-body radiation graph is also compared with the classical model of Rayleigh and Jeans.

$B_{\nu }(\nu ,T)={\frac {8\pi \nu ^{2}}{c^{3}}}\times {\langle E(\nu ,T)\rangle }$

Rayleigh–Jeans Law

The average thermal energy of a classical harmonic oscillator is predicted by equipartition theorem to be,

$\langle E(\nu ,T)\rangle =k_{B}T$

Combined with the Rayleigh model, the blackbody intensity is predicted to be,

$B_{\nu }(\nu ,T)={\frac {8\pi \nu ^{2}}{c^{3}}}\times k_{B}T$

This purely classical theory is known as the Rayleigh–Jeans Law. Although it provides a reasonable description of the intensity of blackbody radiation at low frequencies, it incorrectly predicts that the intensity will continue to increase at higher frequencies, although experiments show that the intensity should reach a maximum and then decline at high frequencies. This is known as the ultraviolet catastrophe.

Planck's Law

$B_{\nu }(\nu ,T)={\frac {8\pi \nu ^{2}}{c^{3}}}\times \langle E(\nu ,T)\rangle$

If we derive the average energy for the oscillator based on the quantum harmonic oscillator, this equations becomes

$B_{\nu }(\nu ,T)={\frac {8\pi \nu ^{2}}{c^{3}}}\times {\frac {h\nu }{\exp \left({\frac {h\nu }{k_{B}T}}\right)-1}}$

Planck's law states that

$B_{\nu }(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\left(h\nu /k_{B}T\right)}-1}},$

where

B_ν(T) is the spectral radiance (the power per unit solid angle and per unit of area normal to the propagation) density of frequency ν radiation per unit frequency at thermal equilibrium at temperature T.

h is the Planck constant;

c is the speed of light in a vacuum;

k_B is the Boltzmann constant;

$\nu$ is the frequency of the electromagnetic radiation;

T is the absolute temperature of the body.

Principles of the Kinetic Theory of Gases

Kinetic Theory of Gases

The kinetic theory of gases is a simple model used to describe the behavior of molecules in the gas phase. It is based on the following assumptions:

1. The gas is made up of a collection of non-interacting particles separated by a distance larger than its dimensions
2. Particles move in random directions such that direction of motion has a negligible effect on the properties of the gas (it is isotropic).
3. All collisions are perfectly elastic. Particles may collide with the walls of the container or with each other.
4. Particles carry only translational kinetic energies.

Given that translational energy spacing is relatively small compared to KT, particles behave classically and follow Newtons law's of motion. In large systems, in is unrealistic to monitor the velocity of individual particles so instead an average is taken. Of the range of possible velocities some will be more common than others, giving rise to a probability distribution, better known as the Maxwell distribution.

The probability that a particle will have a given velocity is provided by the equation below. Ω is the probability density.

$\Omega (v_{x},v_{y},v_{z})dv_{x}dv_{y}dv_{z}=f(v_{x})dv_{x}f(v_{y})dv_{y}f(v_{z})dv_{z}$

Here we have assumed that the probability distributions in each direction are independent of each other, thus it is seperable.

Each particle has translational kinetic energy characterized by

$\varepsilon _{trans}={\frac {1}{2}}m(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})$

The energy distribution is expected to have a form similar of that of the canonical ensemble as follows.

$P(\varepsilon _{trans})\propto e^{-\varepsilon _{trans}/k_{B}T}$

By analogy, the velocity distribution is

$f(v_{i})=Ae^{-{\frac {1}{2}}m(v_{i}^{2})/k_{B}T}$

A is later found to be $A=\left({\frac {m}{2\pi k_{B}T}}\right)^{\frac {1}{2}}$

In order to find the probability of having a particular velocity we must integrate Equation 1 over all space. The function must be normalized such that the probability is unity. The leading coefficient C will take care of this.

$\textstyle \int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\displaystyle \Omega (v_{x},v_{y},v_{z})dv_{x}dv_{y}dv_{z}$

Recall that $e^{a+b}=e^{a}e^{b}$ , which leads to the following.

$\textstyle \int _{-\infty }^{\infty }e^{-{\frac {1}{2}}mv_{x}^{2}/k_{B}T}dv_{x}\int _{-\infty }^{\infty }e^{-{\frac {1}{2}}mv_{y}^{2}/k_{B}T}dv_{y}\int _{-\infty }^{\infty }\displaystyle e^{-{\frac {1}{2}}mv_{z}^{2}/k_{B}T}dv_{z}={\frac {1}{C}}={\frac {1}{A^{3}}}$

The exponentials are of the form of the Gaussian curve and follow

$\textstyle \int _{-\infty }^{\infty }\displaystyle e^{-ax^{2}}{\textrm {d}}x={\sqrt {\frac {\pi }{a}}}$

In this case, $a={\frac {m}{2k_{B}T}}$

Evaluating gives

$C=\left({\frac {m}{2\pi k_{B}T}}\right)^{\frac {3}{2}}$

Since the gas is isotropic the function Ω must depend only on speed. The magnitude of the velocity vector is given as follows.

$\mathbf {v} \cdot \mathbf {v} =u^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}$

Up to this point, everything has been done using Cartesian coordinates. However due to the spherical symmetry of the system is it much more natural to work in spherical coordinates.

The Maxwell Distribution of Molecular Speeds

$$f(v)dv=4\pi v^{2}\left({\frac {m}{2\pi k_{B}T}}\right)^{3/2}e^{-{\frac {1}{2}}mv^{2}/k_{B}T}dv$$

The $4\pi v^{2}$ term comes from the conversion to spherical coordinates (Integrating over the entire surface).

Example

Find the average value of $v_{x}^{2}$ and the kinetic energy associated with motion along the x-direction.

It is best to approach this problem using the Cartesian form since we the integral is simplified considering that the function is independent of y and z.

$\langle v_{x}^{2}\rangle =\textstyle \int \limits _{-\infty }^{\infty }\displaystyle v_{x}^{2}\Omega (v_{x})dx$

$\langle v_{x}^{2}\rangle =\textstyle \left({\frac {m}{2\pi k_{B}T}}\right)^{\frac {1}{2}}\int \limits _{-\infty }^{\infty }\displaystyle v_{x}^{2}e^{-{\frac {1}{2}}m(v_{i}^{2})/k_{B}T}{\textrm {d}}x$

This is an even function, therefore we can integrate over one half of the function then multiply by 2.

$\langle v_{x}^{2}\rangle =2\left({\frac {m}{2\pi k_{B}T}}\right)^{\frac {1}{2}}\int \limits _{0}^{\infty }\displaystyle v_{x}^{2}e^{-{\frac {1}{2}}m(v_{i}^{2})/k_{B}T}{\textrm {d}}x={\frac {k_{B}T}{m}}$

Multiplying this result by ${\frac {1}{2}}m$ will give a kinetic energy of ${\frac {1}{2}}k_{B}T$. For 3 independent direction, the total kinetic energy for an ideal gas in equilibrium is ${\frac {3}{2}}k_{B}T$.

Sources

“Kinetic Theory of Gases and the Boltzmann Equation.” Statistical Mechanics, by Donald A. McQuarrie, New York, 1976.

Engel, Thomas, et al. Physical chemistry, quantum chemistry, and spectroscopy. Pearson Education, Inc., 2019.

Effusion

Effusion of a gas from a container

Consider a container filled with a gas at a given pressure. The container is separated from another container containing no gas (i.e. a vacuum) by a partition with a small hole of surface area $A_{0}$. The gas from the first container will travel through the hole and into the second container at a given rate. This phenomenon is called effusion and the rate at which the gas travels through the hole is called the rate of effusion.

The rate of effusion can be defined as the product of the hole's surface area, $A_{0}$, and the rate at which the particles collide with the walls of the container, $Z_{w}$.

Rate =${\frac {dN}{dt}}=Z_{w}A_{0}$

Where $Z_{w}$ is given by:

$Z_{w}={\frac {p}{\left(2\pi mk_{B}T\right)^{1/2}}}$

Derivation of the time dependancy on pressure

The rate of effusion derived below is the rate with respect to the gas escaping the filled container.

Rate =$-{\frac {dN}{dt}}=-Z_{w}A_{0}={\frac {-pA_{0}}{\left(2\pi mk_{B}T\right)^{1/2}}}$

$N={\frac {pV}{k_{B}T}}$

${\frac {d}{dt}}{\frac {pV}{k_{B}T}}={\frac {-pA_{0}}{\left(2\pi mk_{B}T\right)^{1/2}}}$

${\frac {V}{k_{B}T}}{\frac {dp}{dt}}={\frac {-pA_{0}}{\left(2\pi mk_{B}T\right)^{1/2}}}$

${\frac {dp}{dt}}={\frac {-A_{0}p(k_{B}T)^{1/2}}{V\left(2\pi m\right)^{1/2}}}$

${\frac {dp}{dt}}={\frac {-A_{0}p(k_{B}T)^{1/2}}{V\left(2\pi m\right)^{1/2}}}$

Solving the differential by integration.

${\frac {1}{p}}dp={\frac {-A_{0}}{V}}{\left({\frac {k_{B}T}{2\pi m}}\right)}^{1/2}dt$

$\int _{p_{0}}^{p}\!{\frac {1}{p}}dp=-\int _{0}^{t}\!{\frac {A_{0}}{V}}{\left({\frac {k_{B}T}{2\pi m}}\right)}^{1/2}dt$

$\int _{p_{0}}^{p}\!{\frac {1}{p}}dp=-{\frac {A_{0}}{V}}{\left({\frac {k_{B}T}{2\pi m}}\right)}^{1/2}\int _{0}^{t}\!dt$

$\left[\ln \left(p\right)\right]_{p_{0}}^{p}=-{\frac {A_{0}}{V}}{\left({\frac {k_{B}T}{2\pi m}}\right)}^{1/2}\left[t\right]_{0}^{t}$

$\ln \left(p\right)-\ln \left(p_{0}\right)=-{\frac {A_{0}}{V}}{\left({\frac {k_{B}T}{2\pi m}}\right)}^{1/2}\left(t-0\right)$

$\ln \left({\frac {p}{p_{0}}}\right)=-{\frac {A_{0}}{V}}{\left({\frac {k_{B}T}{2\pi m}}\right)}^{1/2}t$

$p=p_{0}\exp \left[-{\frac {A_{0}}{V}}\left({\frac {k_{B}T}{2\pi m}}\right)^{1/2}t\right]$

Viscosity

What is Viscosity?

The viscosity of a fluid (gas or liquid) is a measurement of the resistance said fluid has to its deformation by stress. For a liquid, this is a relatively easy concept to understand. Water, for example, has a lower viscosity than maple syrup. The concept is slightly less tangible when considering a gas. The system we will analyze in order to better understand the viscosity of a gas is two parallel plates where the gas is contained between them.

In order to establish this relationship, we must consider the bottom plate stationary. That is,

$u_{bottom}=0$

The top plate is considered to be moving with constant velocity. That is,

$u_{top}=U$

where $U$ is a constant velocity.

When a gas is filling the gap between the two plates, the gas molecules exert a force of drag on the motion of the upper plate. This Shear Stress is the previously mentioned force of drag per unit area between the two parallel planes. This relationship is shown by the following formula:

$\tau ={\frac {F(drag)}{A}}$

where $\tau$ is the shear stress of the gas on the motion of the upper plate. The shear stress can also be represented by the relationship:

$\tau =-\eta {\frac {U}{a}}$

where a is the distance between the plates and $\eta$ is the viscosity coefficient of the specific molecule between the plates.

Viscosity Coefficient

As previously mentioned, the viscosity coefficient is a specific constant for the gas being examined. The Kinetic Theory of Gases must be considered in order to derive the equation for the viscosity coefficient. It is assumed from this theory that:

• The particles are hard spheres which implies that elastic collisions occur when particles are within the radius of another molecule.
• The distributions of these velocities follow the Maxwell Distribution of molecular speeds.

From these requirements determined by the Kinetic Theory of Gases, the simple version of the viscosity coefficient can be derived.

$\eta _{simple}={\frac {1}{3}}\left({\frac {2}{\pi }}\right)^{3/2}{\frac {(mk_{B}T)^{1/2}}{\sigma ^{2}}}$

This value of $\eta _{simple}$ is derived by a simple method for the derivation of transport properties of hard spheres. A more rigorous analysis shows that the true values for the viscosity coefficients of gasses follows this formula more closely:

$\eta _{collision}={\frac {5}{16\pi ^{1/2}}}{\frac {(mk_{B}T)^{1/2}}{\sigma ^{2}}}$

The only difference between these two determinations of the viscosity coefficient is the numerical factor. The ratio of these two equations is determined here:

${\frac {\eta _{simple}}{\eta _{collision}}}={\frac {{\frac {1}{3}}\left({\frac {2}{\pi }}\right)^{3/2}}{\frac {5}{16\pi ^{1/2}}}}=0.96$

This ratio shows that the simple derivation is essentially correct and is close enough where the viscosity coefficient of gasses is considered.

When looking at the formula for the viscosity coefficient, it is clear that the viscosity if a gas is not dependent on very many factors. The viscosity coefficient only depends on the mass of the molecule,$m$, the collision cross section, $\sigma$, and the Temperature of the gas. Since the viscosity coefficient of a gas is proportional to the viscosity of the gas, the impacts of these values are outlined below:

• The viscosity of the gas increases as the mass of the molecule increases.
• The viscosity of the gas decreases as the collisional cross section of the molecule increases.
• The viscosity of the gas increases as the temperature of the molecule increases.

These general trends are the most important take away of the viscosity coefficient.

Viscosity Comparisons

We will now look at some examples of the viscosity coefficients of some molecules and determine how the trends outlined above apply. The first example we will look at is the viscosity coefficients of N₂ and CO₂ at 273.15 K. The value of $\eta$ for these molecules respectively are 16.6 and 13.7 respectively. Even though the mass of COTemplate:Sub is much higher than that of N₂, the viscosity coefficient of CO₂ is slightly lower than that of NTemplate:Sub. This is due to the fact that since carbon dioxide is much larger in its collision cross section, this outweighs the fact that it is heavier than nitrogen. This is most because the collision cross section is squared while the mass of the molecule is square-rooted. This concludes that the viscosity coefficient of the molecule depends more on its collision cross section than its mass.

Another example of the phenomenon outlined above is the viscosity coefficients of helium and argon. The viscosity coefficients of these molecules are 29.7 and 21.0 $\times 10^{-5}$ Pa s. Helium is much lighter than argon but it has a much larger viscosity coefficient due to its much smaller collision cross section.

One example which shows a greater dependence on the mass than the collision cross section is shown when examining the viscosity coefficients of argon and krypton. The viscosity coefficients of these molecules at 273.15 K are 21.0 and 23.3 $\times 10^{-5}$ Pa s, respectively. This is because the collision cross sections of the two atoms are relatively close so the masses begin to have a larger impact. The mass of krypton is almost double of that of argon so this drastic difference in mass combined with the relatively close collision cross sections makes it so that the viscosity of krypton is larger than the viscosity of argon.

Thermal conductivity

Thermal Conductivity of a gas based on the Kinetic Theory of Gases

Kinetic Theory of Gases

Systems of gases as described by the Kinetic Theory of Gases

The Kinetic Theory of Gases is a set of assumptions about a system of gas particles. These assumptions consider the system in the classical sense, as opposed to a realistic or quantum system. The gas particles are considered as perfectly round spheres, with each sphere having equal mass. It is assumed that a system has a statistically sufficient number of these spheres. Each sphere is assumed to be experiencing a very large number of collusions with other spheres and the boundaries of the system. These collisions are assumed to be perfectly elastic as there is no loss of energy from either sphere upon impact. It is also assumed that each sphere is in constant, random motion within the system. The velocities of the gas particles follow the Maxwell distribution.

Transport Properties of Gases: Momentum

Using the Kinetic Theory of gases, the function relating the transport of a property through a gas can be determined. One can imagine two parallel plates along an x-axis separated by some amount a of the z-axis. The area between these plates contains many gas particles. The upper plate moves along the x-axis at some constant velocity. A drag force is acted on this movement by the gas particles between the two plates. This is due to the transfer of momentum from the plate to the gas particles. The shear stress ($\tau$) is defined as the drag force per unit area. The magnitude of this drag force is dependent on the velocity of the plate, the spacing between the two plates, and the type of gas particles in the system. Each gas has a constant that effects the drag force. The viscosity coefficient, defined as $\eta$, is proportional to the stress the upper plate exerts.
${\frac {F_{drag}}{A}}=\tau =\eta {\frac {U}{a}}$
The gas particles nearest both plates are assumed to share equal linear momentum in the x-axis to the respective plates. That is the momentum of gas particles near the plate in motion share equal linear momentum in the direction of plate movement. A function of linear momentum in relation to the height on the z-axis is defined as G(x). It is assumed as well that each gas particle at some value on the z-axis (Z) shares the same momentum as all other gas particles at Z. With this assumption, G(x) can be defined as:
$G(x)={\frac {mUz}{a}}$
Gas particles closer to the plate in motion will contain a greater momentum. These gas particles will tend to transfer their momentum to particles closer to the stationary plate. This transfer of momentum is defined as momentum flux, and can be expressed by the rate that momentum is transferred across a plane in the system per unit area, per second. The number of particles crossing a given plane within a given time is constrained by the velocity of any given gas particle to cross the plane. The distance the particle would have to travel to pass through the plane within a given time frame is directly related to the velocity of the particle. The net flux of momentum for particles at some height z’ can be determined by integrating the product of the x-momentum of particles at z’ with the number of particles crossing through a plane. By expressing the momentum of the particles in terms of z on the z-axis and substituting G(z’) in terms of G(z) by use of a Taylor series approximation the viscosity coefficient is defined as:

$\eta ={\frac {1}{3}}\left({\frac {2}{\pi }}\right)^{\frac {3}{2}}{\frac {\left(mk_{b}T\right)^{\frac {1}{2}}}{\sigma ^{2}}}$

Transport Properties of Gases: Kinetic Energy

If the two plates described above are kept stationary but have differing temperatures, a temperature gradient will form between them. Gas particles closer to the higher temperature plate will contain more kinetic energy than the gas particles by the lower temperature plate. This is due to the particles gaining energy when they collide with the higher temperature plate. In much the same way as momentum was transferred through the gas particles, the kinetic energy is also transferred. The rate at which this occurs is measured as the flux (J) of energy through the gas. The flux for a system is equal to the temperature gradient $\left({\frac {dG}{dz}}\right)$ multiplied by the viscosity coefficient ($\eta$). This flux can then be multiplied by the area of the plate to yield the rate of heat transfer. By defining a new function $G(z)=\langle \xi (z)\rangle$ as the average energy of a particle at height z, one can replace $\left({\frac {dG(z)}{dz}}\right)$ in the above equation to determine the thermal conductivity coefficient.
${\frac {dG}{dz}}={\frac {1}{N_{A}}}C_{v,m}{\frac {dT}{dz}}$

$J=-\eta {\frac {dG}{dz}}$

$J=-{\frac {1}{3}}\left({\frac {2}{\pi }}\right)^{\frac {3}{2}}{\frac {\left(mk_{B}T\right)^{\frac {1}{2}}}{\sigma ^{2}}}{\frac {1}{N_{A}}}C_{v,m}{\frac {dT}{dz}}$

$\lambda _{simple}={\frac {1}{3}}\left({\frac {2}{\pi }}\right)^{3/2}\left({\frac {k_{B}T}{m}}\right)^{1/2}{\frac {C_{v,m}}{N_{A}\sigma ^{2}}}$
A more rigorous derivation of the thermal conductivity coefficient based on the Newtonian mechanics of the collisions of gas particles provides a more accurate equation :
$\lambda _{rigorous}={\frac {25}{32}}\left({\frac {k_{B}T}{\pi m}}\right)^{1/2}{\frac {C_{v,m}}{N_{A}\sigma ^{2}}}$

This equation has a different numerical prefactor than the simple derivation, but has the same dependence on the temperature and heat capacity.

Interpretation of Thermal Conductivity

The thermal conductivity coefficient for a gas is independent of its pressure. The amount of gas within a system does not affect the thermal conductivity coefficient. However, the thermal conductivity is dependent on temperature. An increase in temperature relates directly to an increase in a gases thermal conductivity. Gases with a larger radius, $\sigma ^{2}$, have a lower thermal conductivity. This is due to the distance traveled between collisions being shorter. A gas particle with a amount of momentum or kinetic energy will travel a shorter distance towards the lower plate, in the system described above, than a gas with shorter $\sigma$.

Diffusion

Diffusion

Diffusion is the movement of chemicals from an area of high concentration to an area of lower concentration due to random movement of particles. Molecules diffuse so that they are spread out evenly in they space they are occupying, which can effect where a chemical reaction takes place.

Diffusion is pressure, temperature, and mass dependent. Diffusion is slower at high pressure and for heavier particles, and diffusion is faster at high temperatures.

Fick's Law

Fick's law relates the concentration gradient to the rate of diffusion. In other words, the rate of flow of a molecule is related to the concentration gradient of that species and its diffusion coefficient. The equation for the rate of diffusion in one dimension is

$J=-D\operatorname {d} \!\rho _{N}/\operatorname {d} \!x$

where D is the diffusion coefficient, and ρ_N is the number density of the particle.

Diffusion of HCN in air over time based on integrated Fick’s law for diffusion in a 1D space

For particular boundary conditions, Fick's law can be integrated to give the position-dependent number density of the diffusing gases at a function of time.

$\rho _{N}(x,t)=\rho _{N,0}{\text{erfc}}({\sqrt {x/2\surd (Dt)}}$

Diffusion of two Gases

If there are two gases in a container with different masses and velocities, the diffusion coefficients of the gases will be

$D_{N}=1/3l_{N}(v_{N})$

where l is the mean free path length of particle N, and v_N is the average velocity of particle N.

The mean free path length of two component forms is complex due to the fact that more than one type of collision can occur, and the collision cross section of each species is involved,

$l_{1}=4/(4\pi ^{2}\sigma _{1}^{2}\rho _{1,N}+\pi (\sigma _{1}+\sigma _{2})^{2}\rho _{2,N})$

where σ is the collision cross section.

Combining the diffusion coefficient equation and the mean free path length equation, the diffusion coefficient for one particle becomes,

$D_{1}=1/3(4/(4\pi ^{2}\sigma _{1}^{2}\rho _{1,N}+\pi (\sigma _{1}+\sigma _{2})^{2}\rho _{2,N}))(v_{N})$

or,

$D_{1}=1/3(8k_{B}T/\pi m_{2})^{1/2}(4/(4\pi ^{2}\sigma _{1}^{2}\rho _{1,N}+\pi (\sigma _{1}+\sigma _{2})^{2}\rho _{2,N}))$

Self Diffusion

The self diffusion of a gas occurs when there is only one component in the system. Self diffusion occurs constantly as a gas molecule moves around in it's container. It can be observed by isotopic labeling. Since the gas molecules are the same the equation for the diffusion constant simplifies to

$D_{simple}={\frac {1}{3}}\left({\frac {2}{\pi }}\right)^{3/2}\left({\frac {k_{B}T}{m}}\right)^{1/2}{\frac {1}{\rho _{N}\sigma ^{2}}}$

or,

$D_{collision}={\frac {3}{8\pi ^{1/2}}}\left({\frac {k_{B}T}{m}}\right)^{1/2}{\frac {1}{\rho _{N}\sigma ^{2}}}$

for the diffusion coefficient in terms of collisions.

Definition of variables

This section will contain a list of definitions of physical variables used in this book.

Variable	Name	Definition
U	Internal Energy	Internal energy is the total energy needed to create a system. It can be divided into the sum of two other energies (internal kinetic energy and internal potential energy).
H	Enthalpy	Enthalpy is a thermodynamic variable which corresponds to the total energy of the system and the energy required to create a volume. It has units of energy and can be calculated using the equation H = U +pV
q	Heat	The thermal energy transferred from the surroundings to the system.
w	Work	The energy corresponding to the expansion of the system against the surroundings.
S	Entropy	Changes in the state of a system can also involve a change in the degree of disorder in the system and surroundings. The thermodynamic function entropy corresponds to this disorder.
A	Helmholtz Energy	The change in energy found within a canonical ensemble. This can be calculated by the following equation: A = U - T x S
G	Gibb's Energy	The change in energy found within an isothermal-isobaric ensemble. This can be calculated by the following equation: G = H - T x S
I	Inertia	The moment of inertia is what the rotation of an object depends on.
Q	Partition Function	The sum over all states of a system. It is used in the denominator of the Boltzmann distribution.
μ	Chemical Potential	For the canonical ensemble, the chemical potential, is the Helmholtz free energy change when a particle is added to the system.
F	Fraction of Molecules at a Given Speed	The fraction of molecules within a range of speed (F) is an integral over the probability distribution.
ℓ	Mean Free Path	The mean free path is the average distance that a molecule can travel before it will undergo a collision.
τ	Shear Stress	The drag force per unit area.
J	Momentum Flux	The rate that momentum passes through a plane per unit area, per unit second

Equations for reference

Equation Sheet 1

Translational States

The translational energy of a particle in a 3 dimensional box is given by the equation:

$E_{n_{x},n_{y},n_{z}}={h^{2} \over 8m}\left({{{n_{x}}^{2}} \over {a^{2}}}+{{{n_{y}}^{2}} \over {b^{2}}}+{{{n_{z}}^{2}} \over {c^{2}}}\right)$

Where h is Planck's constant $(6.626068\times 10^{-34}Js)$, m is the mass of the particle in kg, n is the translational quantum number for the denoted direction of translation (x, y, z) and a, b, and c are the length of the box in the x, y, and z directions respectively. The translational quantum number, n, may possess any positive integer value.

Rotational States

The moment of inertia for a rigid rotor is given by the equation:

$I=\sum _{i}{m_{i}}{r_{i}^{2}}$

where m_i is the mass an atom in the molecule and r_i is the distance in meters from that atom to the molecule's center of mass. For a diatomic molecule this formula may be simplified to:

$I=\mu {r_{e}^{2}}$

where r_e is the internuclear distance and μ is the reduced mass for the diatomic molecule:

$\mu ={{m_{1}}{m_{2}} \over {m_{1}+m_{2}}}$

In the case of a homonuclear diatomic molecule, the reduced mass, μ, can be further simplified to:

$\mu ={{m_{1}}{m_{1}} \over {m_{1}+m_{1}}}={{m_{1}^{2}} \over {2m_{1}}}={{m_{1}} \over {2}}$

The energy of a rigid rotor occupying a rotational quantum state J (J = 0,1,2,...) is given by the equation:

$E_{J}={{\hbar }^{2} \over 2\mu {r_{e}^{2}}}J(J+1)$

where $\hbar ={h \over 2\pi }$ and the degeneracy of each rotational state is given by $g_{J}=2J+1$.

The frequency of radiation corresponding to the energy of rotation at a given rotational quantum state is given by:

${\tilde {\nu }}=2{\tilde {B}}(J+1)$

where ${\tilde {B}}$ is the rotational constant, and can be related to the moment of inertia by the equation:

${\tilde {B}}={h \over {8{\pi }^{2}cI}}$

where c is the speed of light.

To avoid confusing in obtaining values for the frequency of radiation, ${\tilde {\nu }}$, and the rotational constant, ${\tilde {B}}$, c is often expressed in units of cm/s ($c=2.99792458\times 10^{10}cm/s$)

Vibrational States

The energy of a simple harmonic oscillator is given by the equation:

$E_{n}=h\nu (n+{1 \over 2})$

where n = 0,1,2,... is the vibrational quantum number and ν is the fundamental frequency of vibration, given by:

$\nu ={1 \over 2\pi }{\sqrt {k \over \mu }}$

where k is the bond force constant.

Electronic States

An electron in an atom may be described by four quantum numbers: the principle quantum number, $n=1,2,...$; the angular momentum quantum number, $l=0,1,...,(n-1)$; the magnetic quantum number, $m_{l}=-l,-l+1,...,l-1,l$; the spin quantum number, $m_{s}=\pm {1 \over 2}$.

For a hydrogen-like atom (possessing only a single electron), the energy of the electron is given by the equation:

$E_{n}=-\left({{{m_{e}}e^{4}} \over {32{\pi }^{2}{\epsilon }_{0}^{2}{\hbar }^{2}}}\right){1 \over n^{2}}$

where $m_{e}$ is the mass of an electron, e is the charge of an electron, and ${\epsilon }_{0}$ is the permittivity of free space.

For a system with multiple electrons, the total spin for the system is given the sum:

$S=\sum _{i}m_{s,i}$

The electronic degeneracy of the system may then be determined by

$g_{el}=2S+1$.

Thermodynamic Relations

There exist a number of equations which allow for the relation of thermodynamic variables, such that it is possible to determine values for many of these variables mathematically starting with just a few:

$H=U+pV$

where H is enthalpy, U is internal energy, p is pressure, and V is volume;

$G=H-TS$

where G is Gibbs energy, T is temperature and S is entropy;

$A=U-TS$

where A is Helmholtz energy;

$\Delta U=q+w$

where q is heat and w is work;

$dS={dq_{rev} \over T}$

where $dq_{rev}$ is the heat associated with a reversible process;

$pV=nRT$

where n is the number of moles of a gas and R is the ideal gas constant ($8.314JK^{-1}mol^{-1}$).

The heat capacity for a gas at constant volume may be estimated by the differential:

$C_{v}=\left({\partial U \over \partial T}\right)_{V,n}$

while pressure may be estimated by the similar calculation:

$p=-({\partial U \over \partial V})_{n}$

$C_{v}$ allows for the determination of q:

$q=C_{v}\Delta T$

$C_{v}$ may also be related to the heat capacity at constant pressure:

$C_{p}=C_{v}+nR$

which in turn allows for the determination of enthalpy:

$\Delta H=C_{p}\Delta T$

Overall heat capacity in each case may be related to molar heat capacity by relating the number of moles of gas:

$C_{v}=nC_{v}^{m}$

$C_{p}=nC_{p}^{m}$

Finally, the internal energy contribution from translational, rotational, and vibrational energies of a gas may be determined by the equation:

$U={1 \over 2}n_{trans}nRT+{1 \over 2}n_{rot}nRT+n_{vib}nRT$

where $n_{trans},n_{rot},n_{vib}$ are the translational, rotational, and vibrational degrees of freedom for the molecule, respectively.

For linear molecules the internal energy simplifies to:

$U={3 \over 2}nRT+nRT+(3n_{atom}-5)nRT$

And for non-linear molecules:

$U={3 \over 2}nRT+{3 \over 2}nRT+(3n_{atom}-6)nRT$

Equation Sheet 2

Formula to calculate the internal energy is given by the formula

$U=\langle E\rangle ={\sum _{j}{E_{j}}{\exp(-E_{j}/{k_{B}}T)} \over Q}$

Where U is the internal energy of the system ${E_{j}}$ is the energy of the system, $k_{B}$ is the Boltzmann constant (1.3807 x 10^-23 J K^-1), T is the temperature in Kelvin, and Q is the partition function of the system.

Canonical Ensemble

Internal Energy, U, of Canonical Ensemble:

$U=\langle E\rangle =k_{B}T^{2}\left({\partial \ln Q \over \partial T}\right)_{N,V}$

Where $k_{B}$ is the Boltzmann constant, T is the temperature in Kelvin, and Q is the partition function of the system.

Entropy, S, of the Canonicial Ensemble:

$S={\langle E\rangle \over T}+k_{B}\ln Q$

Where E is the ensemble average energy of the system, $k_{B}$ is the Boltzmann constant, T is the temperature in Kelvin, and Q is the partition function of the system.

Helmholtz Free Energy, A, of the Canonical Ensemble

$A=-k_{B}T\ln Q$

Where $k_{B}$ is the Boltzmann constant, T is the temperature in Kelvin, and Q is the partition function of the system.

Partition Functions

Function to calculate the partition function, Q, in a system of N identical indistinguishable particles can be calculated by:

$Q={q^{N} \over N!}$

Where q is the molecular partition functions.

Molecular Partition Function

$q=q_{trans}q_{rot}q_{vib}q_{elec}$

In which q is the molecular partition function, $q_{trans}$ is the molecular partition function of the translational degree of freedom, $q_{rot}$ is the molecular partition function of the rotational degree of freedom, $q_{vib}$ is the molecular partition function of the vibrational degree of freedom, and $q_{elec}$ is the molecular partition function of the electronic degree of freedom.

Molecular Translational Partition Function

$q_{trans}=\left({2\pi mk_{B}T \over h^{2}}\right)^{3 \over 2}\times V$

Where $q_{trans}$ is the molecular partition function of the translational degree of freedom, $k_{B}$ is the Boltzmann constant, m is the mass of the molecule, T is the temperature in Kelvin, V is the volume of the system.

To simplify the calculation, the de Broglie wavelength, Λ, of the molecule at a given temperature may be used. The de Broglie wavelength is defined as:

$\Lambda =\left({2\pi mk_{B}T \over h^{2}}\right)^{-1/2}$

This simplifies the translational molecular partition function to:

$q_{trans}={V \over \Lambda ^{3}}$

Molecular Rotational Partition Function

$q_{rot}={8{\pi }^{2}k_{B}T\mu r_{e}^{2} \over \sigma h^{2}}={2k_{B}T\mu r_{e}^{2} \over \sigma {\hbar }^{2}}$

Where $q_{rot}$ is the molecular partition function of the rotational degree of freedom, T is the temperature in Kelvin, ${k_{B}}$ is the Boltzmann constant, $r_{e}$ is the bond length of the molecule, μ is the reduced mass, h is Planck's constant, $\hbar$ is defined as $h \over {2\pi }$, and σ is the symmetry factor (σ = 2 for homonuclear molecules and σ = 1 for heteronuclear molecules).

The constants in the rotational molecular partition function can be simplified to the characteristic temperature, Θ_r, which has units of Kelvin:

$\Theta _{r}={h^{2} \over {8{\pi }^{2}k_{B}\mu r_{e}^{2}}}={{\hbar }^{2} \over {2k_{B}\mu r_{e}^{2}}}$

Using the characteristic temperature, the rotational molecular partition function is simplified to:

$q_{rot}={T \over {\sigma \Theta _{r}}}$

Molecular Vibrational Partition Function

$q_{vib}={1 \over {1-\exp \left({{-hv} \over {k_{b}T}}\right)}}$

Where $q_{vib}$ is the molecular partition function of the vibrational degree of freedom, T is the temperature in Kelvin, $k_{B}$ is the Boltzmann constant, h is Planck's constant, and υ is the vibrational frequency of the molecule defined as:

$\nu ={1 \over {2\pi }}\left({k \over \mu }\right)^{1/2}$

Where k is the spring constant of the molecule and μ is the reduced mass of the molecule.

The characteristic temperature Θ_υ may be used to simplify the constants in the molecular vibrational partition function to the following:

$\Theta _{\nu }={h\nu \over k_{B}}$

Using the characteristic temperature, the vibrational molecular partition function is simplified to:

$q_{vib}={1 \over {1-\exp \left({-\Theta _{\nu } \over T}\right)}}$

Molecular Electronic Partition Function

$q_{elec}=g_{1}$

Where $q_{elec}$ is the molecular partition function of the electronic state and g₁ is the degeneracy of the ground state.

For large temperatures, the equation turns to:

$q_{elec}=g_{1}\exp \left({D_{0} \over k_{B}T}\right)$

Where D₀ is the bond dissociation energy of the molecule, and $k_{B}$ is the Boltzmann constant.

Simplified Molecular Partition Function

All molecular partition functions combined are defined as:

$q={\left({2\pi mk_{B}T \over h^{2}}\right)^{3 \over 2}V\times \left({2k_{B}T\mu r_{e}^{2} \over \hbar ^{2}}\right)\times \left({1 \over 1-\exp \left({-hv \over k_{B}T}\right)}\right)\times g_{1}}$

Which simplifies further when utilizing the de Broglie wavelength for the translational molecular partition function and the characteristic temperatures for the rotational and vibrational molecular partition functions.

$q={V \over \Lambda ^{3}}\times {T \over \sigma \Theta _{r}}\times {1 \over 1-\exp \left({-\Theta _{\nu } \over T}\right)}\times g_{1}$

Which is equivalent to:

$q=q_{trans}q_{rot}q_{vib}q_{elec}$

Chemical Equilibrium

Determination of equilibrium constant $K_{c}$ is found by the following equation:

$K_{c}(T)={((q_{C}/V)^{\nu _{C}}(q_{D}/V)^{\nu _{D}}) \over ((q_{A}/V)]^{\nu _{A}}(q_{B}/V)^{\nu _{B}})}={{\rho _{C}}^{\nu _{C}}{\rho _{D}}^{\nu _{D}} \over {\rho _{A}}^{\nu _{A}}{\rho _{B}}^{\nu _{B}}}$

In which q_A, q_B, q_C, and q_D are partition functions of each species and with corresponding ν and ρ values for corresponding stoichiometric coefficients and partial pressures.

The equilibrium constant in terms of pressure can be expressed as;

$K_{p}(t)={{\rho _{C}}^{\nu _{C}}{\rho _{D}}^{\nu _{D}} \over {\rho _{A}}^{\nu _{A}}{\rho _{B}}^{\nu _{B}}}=(k_{B}T)^{\nu _{C}+\nu _{D}-\nu _{A}-\nu _{B}}K_{c}(T)$

The chemical potential can be determined by

$\mu _{i}=-k_{B}T^{2}\ln({q_{i}(V,T) \over N_{i}})$

in which $\mu _{i}$ is the change in Helmholtz energy when a new particle is added to the system

The pressure, p, can then be determined by

$p=k_{B}T({\partial \ln Q \over \partial V})_{N,T}$

Data

Molecule	$\Theta _{r}$(K)	$\Theta _{v}$(K)
H2	87.547	6332.52
N2	2.0518	3393.54
O2	2.0793	2273.60
F2	1.2808	1318.87
HF	41.345	5954.27
HCl	15.240	4303.41
NO	2.4524	2739.79
C2H2	1.7012

Example

Calculate the ground state characteristic rotational ($\Theta _{r}$) and characteristic vibrational ($\Theta _{v}$) temperatures for molecular hydrogen, H₂.

$\Theta _{r}={\frac {\hbar ^{2}}{2k_{B}\mu {r_{e}}^{2}}}$

Where ${\bar {h}}=h/2\pi$ is the reduced Planck constant, $r_{e}$ is the internuclear distance for ground state hydrogen, $k_{B}$ is the Boltzmann constant, and $\mu$ is the reduced mass.

$\Theta _{r}={\frac {{1.0546\times 10^{-34}{\text{J s}}}^{2}}{2{1.3806\times 10^{-23}{J \over K}}\times {8.35942\times 10^{-28}{\text{kg}}}\times {{7.4144\times 10^{-11}{\text{m}}}^{2}}}}$

$\Theta _{r}={\frac {1.11212\times 10^{-68}{\text{J}}^{2}{\text{s}}^{2}}{1.2703\times 10^{-70}{\text{J}}^{2}{\text{K}}^{-1}}}$

$\Theta _{r}=87.54_{7}{\text{K}}$

The characteristic vibrational temperature ($\Theta _{v}$) is calculated using the following equation

$\Theta _{v}={\frac {h\nu }{k_{B}}}$

Where $h$ is Planck's constant, $k_{B}$ is the Boltzmann constant, and $\nu$ is the vibrational frequency of the molecule. To retain units of K the vibrational frequency must be changed to units of s^-1.

$\Theta _{v}={\frac {{6.6261\times 10^{-34}{\text{J s}}}\times {4401.21{\text{cm}}^{-1}}\times {2.998\times 10^{10}{cm \over s}}}{1.3806\times 10^{-23}{J \over K}}}$

$\Theta _{v}=6332.5_{2}{\text{K}}$

Essential mathematics for statistical thermodynamics

Exponentials and Logarithms

Exponential functions in Statistical Thermodynamics play an important role. Most of the functions that are used in this area follow a gaussian distribution. Meaning, a normalized exponential function. Therefore, it is important the understanding of some of the basic properties of this type of functions.

In mathematics, exponential functions are in the form of:

$f(x)=b^{x}$

Where $b$ is any constant, and $x$ appears as an exponent. This functions have the particularity to have a close relationship between its derivative and the function itself, due to direct relationship between both of them. However, probably the most relevant exponential function for the Statistical Thermodynamics has to be the exponential function with a base equal to Euler number ($e\approx 2.71828...$), which is the only constant of proportionality between its derivative and the function is 1.

On the other hand, exponential functions have logarithms as their inverse function, having the form of:

$f(x)=\log _{b}(x)$

This function, also has a particular a relevant significance due to its mathematical properties. It is important to highlight that, along with the exponential function with base , logarithms with base $e$ are called natural logarithms.

Some of the properties of the exponential functions are:

• $e^{x+y}=e^{x}e^{y}\,$
• $e^{0}=1\,$
• $e^{x}\neq 0$
• ${\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}$
• $\left(e^{x}\right)^{n}=e^{nx},n\in \mathbb {Z}$

Some of the properties of logarithm functions are:

• $\log _{b}(xy)=\log _{b}x+\log _{b}y$
• $\log _{b}\!{\frac {x}{y}}=\log _{b}x-\log _{b}y$
• $\log _{b}\left(x^{p}\right)=p\log _{b}x$
• $\log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}$

See Also

• Wikipedia:Exponential_function
• Wikipedia:Logarithm
• Wikipedia:Series_(mathematics)

Tips for deriving relations with partition functions

Use the rules of logarithms

You can use the rules of logarithms to isolate terms.

${\textrm {ln}}(ab)={\textrm {ln}}(a)+{\textrm {ln}}(b)$

${\textrm {ln}}\left({\frac {a}{b}}\right)={\textrm {ln}}(a)-{\textrm {ln}}(b)$

Derivatives of Constants are Equal to Zero

If you are taking a derivative of a function, you can use the rules of logarithms to isolate a term that depends on that variable. Now, you only need to take the derivative on this term. the derivatives of all other terms will be zero

${\frac {\partial {\textrm {ln}}(xy)}{\partial x}}={\frac {\partial {\textrm {ln}}(x)}{\partial x}}+{\frac {\partial {\textrm {ln}}(y)}{\partial x}}$

${\frac {\partial {\textrm {ln}}(xy)}{\partial x}}={\frac {\partial {\textrm {ln}}(x)}{\partial x}}+{\frac {\partial {\textrm {ln}}(y)}{\partial x}}$

${\frac {\partial {\textrm {ln}}(xy)}{\partial x}}={\frac {\partial {\textrm {ln}}(x)}{\partial x}}+0$

${\frac {\partial {\textrm {ln}}(xy)}{\partial x}}={\frac {\partial {\textrm {ln}}(x)}{\partial x}}$

Lagrange multipliers

Constrained Optimization

When constraints are imposed on a system, Lagrange multipliers can be incorporated to determine the maximum of the multivariable function. The new process for determining maximum of this function within the constraint becomes:

1. Write the constraint as a function. i.e., $g(x,y)=c$
2. Define a new equation. $f(x,y)+{\alpha }({g(x,y)}-{c})$ where $\alpha$ is an undefined constant
3. Solve this set of equations to find the maximum, using the previous three steps for determining the maximum of an unconstrained system.

For example, suppose we have a function $f(x,y)=-{2x}^{2}-{y}^{2}-{xy}-{10y}$ and we impose the following constraint upon the function: $y=x+5$

The constraint would be written as $g(x,y)=x+y=5$

We would then define the new equation following the constraint as $(-{2x}^{2}-{y}^{2}-{xy}-{10y})+{\alpha }({x}+{y}-{5})$

Next, we take the partial derivative with respect for both x and y, set it to zero, and solve for x and y.

First of all taking the partial derivative with respect for x set to zero:

${\frac {\partial }{\partial x}}[(-{2x}^{2}-{y}^{2}-{xy}-{10y})+{\alpha }({x}+{y}-{5})]=0$

Evaluating this will give:

${\alpha }-4x-y=0$

${\alpha }=4x+y$

Now, the partial derivative with respect for y set to zero will be taken:

${\frac {\partial }{\partial y}}[(-{2x}^{2}-{y}^{2}-{xy}-{10y})+{\alpha }({x}+{y}-{5})]=0$

${\alpha }-x-2y-10=0$

${\alpha }=x+2y+10$

This leads to the following system of equations that can be solved to determine the maximum:

${\alpha }=4x+y$

${\alpha }=x+2y+10$

$x+y=5$

From Solving this set of equations the maximum subjected to the constraint of $x+y=5$ is found to be:

$(x,y)=\left({\frac {-35}{8}},{\frac {5}{8}}\right)$

Unconstrained Optimization

Determining the maximum of an unconstrained system follows very similar steps it just will not have a lagrange multiplier as the system is not subjected to the

maximum along a given line, rather the maximum of the system itself. The steps to solve an unconstrained system becomes:

1. Calculate the partial derivatives
2. set them to zero
3. solve for the variables

For example given the same function of $f(x,y)=-{2x}^{2}-{y}^{2}-{xy}-{10y}$ first the partial derivatives will be calculated to be:

$({\frac {\partial f}{\partial x}})_{y}=-4x-y$

$({\frac {\partial f}{\partial y}})_{x}=-2y-x$

Let both partial derivatives be zero:

$-4x-y=0$

$-2y-x=0$

Finally the variables will be solved for. Giving a maximum that is different than that of the constrained system:

$(x,y)=\left({\frac {10}{7}},{\frac {-40}{7}}\right)$

Translational partition function

Derivation of Translational Partition Function

A Molecular Energy State or is the sum of available translational, vibrational, rotational and electronic states available. The Translational Partition Function gives a "sum over" the available microstates.

$q_{trans}=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{3/2}V$

The derivation begins with the fundamental partition function for a canonical ensemble that is classical and discrete which is defined as:

$q=\sum _{j}^{\infty }e^{-\beta \epsilon _{j}}$

where j is the index, $\beta ={\frac {1}{k_{B}T}}$ and $\epsilon _{j}$is the total energy of the system in the microstate

For a particle in a 3D box with length $L$, mass $m$ and quantum numbers $n_{x},n_{y},n_{z}$ the energy levels are given by:

$\epsilon _{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8mL^{2}}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})$

Substituting the energy level equation $\epsilon _{n_{x},n_{y},n_{z}}$ for $\epsilon _{j}$ in the partition function

$q_{trans}=\sum _{j}^{\infty }e^{-\beta [{\frac {h^{2}}{8mL^{2}}}(n_{x}^{2}+n_{y}^{2}+n_{z}^{2})]}$

$q_{trans}=\sum _{n_{x},n_{y},n_{z}=1}^{\infty }e^{-\beta [{\frac {h^{2}}{8mL^{2}}}(n_{x}^{2})]}e^{-\beta [{\frac {h^{2}}{8mL^{2}}}(n_{y}^{2})]}e^{-\beta [{\frac {h^{2}}{8mL^{2}}}(n_{z}^{2})]}$

Using rules of summations we can split the above formula into a product of three summation formulas

$q_{trans}=\sum _{n_{x}=1}^{\infty }e^{-\beta {\frac {h^{2}}{8mL^{2}}}(n_{x}^{2})}\sum _{n_{y}=1}^{\infty }e^{-\beta {\frac {h^{2}}{8mL^{2}}}(n_{y}^{2})}\sum _{n_{z}=1}^{\infty }e^{-\beta {\frac {h^{2}}{8mL^{2}}}(n_{z}^{2})}$

Defining the dimensions of the box (Particle In A Box Model) in each direction to be equivalent $n_{x}=n_{y}=n_{z}$

$q_{trans}={\Bigg [}\sum _{n=1}^{\infty }e^{-\beta {\frac {h^{2}}{8mL^{2}}}(n^{2})}{\Bigg ]}^{3}$

Because the spacings between translational energy levels are very small they can be treated as continuous and therefore approximate the sum over energy levels as an integral over n

$\sum _{n=1}^{\infty }e^{-\beta {\frac {h^{2}}{8mL^{2}}}(n^{2})}\approx \int _{0}^{\infty }e^{-\beta {\frac {h^{2}}{8mL^{2}}}(n^{2})}\,dn$

Using the substitutions $\alpha =\beta {\frac {h^{2}}{8mL^{2}}}$ and $n=x$ The integral simplifies to

$\int \limits _{0}^{\infty }e^{-\alpha x^{2}}\,dx$

From The list of definite integrals the simplified integral has a known solution:

$q_{trans}=\int \limits _{0}^{\infty }e^{-\alpha x^{2}}\,dx={\frac {1}{2}}{\sqrt {\frac {\pi }{\alpha }}}$

Therefore,

$q_{trans}={\Bigg (}{\frac {1}{2}}{\sqrt {\frac {\pi }{\alpha }}}{\Bigg )}^{3}$

Re-substituting $\alpha =\beta {\frac {h^{2}}{8mL^{2}}}$ and $\beta ={\frac {1}{k_{B}T}}$

$q_{trans}={\Bigg (}{\frac {1}{2}}{\sqrt {\frac {\pi }{\beta {\frac {h^{2}}{8mL^{2}}}}}}{\Bigg )}^{3}$

$q_{trans}={\Bigg (}{\sqrt {\frac {2\pi mk_{B}TL^{2}}{h^{2}}}}{\Bigg )}^{3}$

Since $L$ is length and $L^{3}=V$

$q_{trans}={\Bigg (}{\frac {2\pi mk_{B}T}{h^{2}}}{\Bigg )}^{3/2}V$

Rotational partition function of a linear molecule

Derivation

The rotational partition function, $Q_{rot}$ is a sum over state calculation of all rotational energy levels in a system, used to calculate the probability of a system occupying a particular energy level. The open form of the partition function is an infinite sum, as shown below. By making a few substitutions and replacing the sum with an integral, an algebraic expression for the rotational partition function can be derived. $I=\mu {r_{e}}^{2}$ $q=\sum _{j}^{\infty }g_{j}\exp \left({\frac {-E_{j}}{k_{B}T}}\right)$

The degeneracy, g, of a rotational energy level, j, is the number of different measurable states that have the same energy. For rotational energy levels, this is given by:

$g=2J+1$

The rotational energy of a molecule is:

$E_{J}={\frac {\hbar ^{2}}{2I}}J(J+1)$

Substituting these values into the open form of the partition function, we get

$q_{rot}=\sum _{j}^{\infty }(2J+1)\exp \left({\frac {-\hbar ^{2}}{2k_{B}TI}}J(J+1)\right)$

Since the spacings of the rotational energy levels is small, the sum can be approximated as an integral over J,

$q_{rot}=\int _{0}^{\infty }(2J+1)\exp \left({\frac {-\hbar ^{2}}{2k_{B}TI}}J(J+1)\right){\textrm {d}}J$

From a table of integrals:

$\int (2x+1)\exp(-ax(x+1)){\textrm {d}}x={\frac {\exp(-ax(x+1))}{a}}$

Letting x = J and $a={\frac {-\hbar ^{2}}{2k_{B}TI}}$ we get

$q_{rot}={-{\frac {-\exp(-ax(x+1))}{a}}}{\bigg |}_{0}^{\infty }$

$=0-{\frac {1}{a}}=-{\frac {1}{a}}$

$={\frac {2k_{B}TI}{\hbar ^{2}}}$

A symmetry factor $\sigma$ is introduced to account for the nuclear spin states of homonuclear diatomic molecules. $\sigma$ has a value of 2 for homonuclear diatomics and 1 for other linear molecules.

$q_{rot}={\frac {2k_{B}TI}{\hbar ^{2}\sigma }}$

The rotational characteristic temperature $\theta _{rot}$ is introduced to simplify the rotational partition function expression.

$\theta _{rot}={\frac {\hbar ^{2}}{2k_{B}I}}$

The physical meaning of the characteristic rotational temperature is an estimate of which thermal energy is comparable to energy level spacing. Substituting this into the partition function gives us

$q_{rot}={\frac {T}{\sigma \theta _{rot}}}$

Vibrational partition function of a diatomic molecule

The general form of the molecular partition function is an infinite sum which is open form, making it difficult to calculate, this is why the sum is approximated as a closed form which leads to an algebraic equation. The derivation of the closed form on the equation is as follows:

The open form of the vibrational partition function:$q_{vib}=\sum _{j}g_{j}\exp \left({\frac {-\epsilon _{j}}{k_{B}T}}\right)$

solving for $\epsilon _{j}$

$\epsilon _{j}$$=E_{j}-E_{0}$

$\epsilon _{j}$$=$$h\nu$ $(j+{\frac {1}{2}})$$-h\nu$$(0-{\frac {1}{2}})$

$\epsilon _{j}$$=h\nu$$j$$-$ ${\frac {1}{2}}$ $h\nu$$-$${\frac {1}{2}}$$h\nu$$=h$$\nu$$j$

(where j=0,1,2...)

and by substituting $g_{j}$$=1$ (i.e., singly degenerate) into the summation for $q_{vib}$ the resulting equation is:

$q_{vib}=\sum _{j=0}^{\infty }$$\exp \left({\frac {-h\nu j}{k_{B}T}}\right)=\sum _{j=0}^{\infty }[\exp \left({\frac {-h\nu }{k_{B}T}}\right)]^{j}$ The j is taken outside the brackets by the common exponent rule: $\exp(ab)=\exp(a)\exp(b)$

Note that $E_{n}$$=$$h\nu (n+{\frac {1}{2}})$ is the equation that represents the energy levels of a harmonic oscillator which is used to approximate the vibrational molecular degree of freedom. The vibrational zero point energy is not negligible and must be defined at n=0.

Next, in order for the open system to be converted into the closed system, the equation must take the form of a geometric series identity, like in calculus.

if x<1, $\sum _{i=0}^{\infty }$$x^{i}$$=$ ${\frac {1}{1-x}}$

This is done by first letting $e^{\left({\frac {-h\nu }{k_{B}T}}\right)}$ $=x$

Then, $q_{vib}=\sum _{j=0}^{\infty }$ $x^{j}$

this converges when x<1, giving ${\frac {1}{1-x}}$ and by replacing x with the original expression, you have:

$q_{vib}=$${\frac {1}{1-\exp \left({\frac {-h\nu j}{k_{B}T}}\right)}}$

where $\nu$ is the vibrational frequency of the molecule, which can by found by the following equation: $\nu$=${\frac {1}{2\pi }}$$\left({\frac {k}{\mu }}\right)^{\frac {1}{2}}$

where k is the spring constant of the molecule and $\mu$ is the reduced mass

Example

Calculate the population of the ground vibrational state of $N_{2}$ at 298.15 K. ($\nu =7.072\times 10^{13}s^{-1}$)

$q_{vib}={\frac {1}{1-\exp \left({\frac {-h\nu j}{k_{B}T}}\right)}}$

$={\frac {1}{1-\exp \left({\frac {-(6.626068\times 10^{-34}Js\times 7.072\times 10^{13}s^{-1}}{1.3807\times 10^{-23}JK^{-1}\times 298.15K}}\right)}}=1.000011$

Next the Probability of the ground state can be calculated: $P_{0}={\frac {\exp \left({\frac {-E_{0}}{k_{B}T}}\right)}{q_{vib}}}={\frac {\exp(0)}{1.000011}}=0.999998$

This means that 99.9998% of all $N_{2}$ molecules are in the ground vibrational state at 298.15 K.