Discrete Mathematics/Print version
| This is the print version of Discrete Mathematics You won't see this message or any elements not part of the book's content when you print or preview this page. |
The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/Discrete_Mathematics
Introductory discrete mathematics
editSet Theory
editIntroduction
editSet Theory starts very simply: it examines whether an object belongs, or does not belong, to a set of objects which has been described in some non-ambiguous way. From this simple beginning, an increasingly complex (and useful!) series of ideas can be developed, which lead to notations and techniques with many varied applications.
Definition: Set
editThe present definition of a set may sound very vague. A set can be defined as an unordered collection of entities that are related because they obey a certain rule.
'Entities' may be anything, literally: numbers, people, shapes, cities, bits of text, ... etc
The key fact about the 'rule' they all obey is that it must be well-defined. In other words, it must describe clearly what the entities obey. If the entities we're talking about are words, for example, a well-defined rule is:
X is English
A rule which is not well-defined (and therefore couldn't be used to define a set) might be:
X is hard to spell
- where X is any word
Elements
editAn entity that belongs to a given set is called an element of that set. For example:
Henry VIII is an element of the set of Kings of England. : kings of England {Henry VIII}
Set Notation
edit- To list the elements of a set, we enclose them in curly brackets, separated by commas. For example:
- The elements of a set may also be described verbally:
- The set builder notation may be used to describe sets that are too tedious to list explicitly. To denote any particular set, we use the letter :
- or equivalently
- The symbols and denote the inclusion and exclusion of element, respectively:
- Sets can contain an infinite number of elements, such as the set of prime numbers. Ellipses are used to denote the infinite continuation of a pattern:
Note that the use of ellipses may cause ambiguities, the set above may be taken as the set of integers individible by 4, for example.
- Sets will usually be denoted using upper case letters: , , ...
- Elements will usually be denoted using lower case letters: , , ...
Special Sets
editThe universal set
editThe set of all the entities in the current context is called the universal set, or simply the universe. It is denoted by .
The context may be a homework exercise, for example, where the Universal set is limited to the particular entities under its consideration. Also, it may be any arbitrary problem, where we clearly know where it is applied.
The empty set
editThe set containing no elements at all is called the null set, or empty set. It is denoted by a pair of empty braces: or by the symbol .
It may seem odd to define a set that contains no elements. Bear in mind, however, that one may be looking for solutions to a problem where it isn't clear at the outset whether or not such solutions even exist. If it turns out that there isn't a solution, then the set of solutions is empty.
For example:
- If then .
- If then .
Operations on the empty set
editOperations performed on the empty set (as a set of things to be operated upon) can also be confusing. (Such operations are nullary operations.) For example, the sum of the elements of the empty set is zero, but the product of the elements of the empty set is one (see empty product). This may seem odd, since there are no elements of the empty set, so how could it matter whether they are added or multiplied (since “they” do not exist)? Ultimately, the results of these operations say more about the operation in question than about the empty set. For instance, notice that zero is the identity element for addition, and one is the identity element for multiplication.
Special numerical sets
editSeveral sets are used so often, they are given special symbols.
Natural numbers
editThe 'counting' numbers (or whole numbers) starting at 1, are called the natural numbers. This set is sometimes denoted by N. So N = {1, 2, 3, ...}
Note that, when we write this set by hand, we can't write in bold type so we write an N in blackboard bold font:
Integers
editAll whole numbers, positive, negative and zero form the set of integers. It is sometimes denoted by Z. So Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
In blackboard bold, it looks like this:
Real numbers
editIf we expand the set of integers to include all decimal numbers, we form the set of real numbers. The set of reals is sometimes denoted by R.
A real number may have a finite number of digits after the decimal point (e.g. 3.625), or an infinite number of decimal digits. In the case of an infinite number of digits, these digits may:
- recur; e.g. 8.127127127...
- ... or they may not recur; e.g. 3.141592653...
In blackboard bold:
Rational numbers
editThose real numbers whose decimal digits are finite in number, or which recur, are called rational numbers. The set of rationals is sometimes denoted by the letter Q.
A rational number can always be written as exact fraction p/q; where p and q are integers. If q equals 1, the fraction is just the integer p. Note that q may NOT equal zero as the value is then undefined.
- For example: 0.5, -17, 2/17, 82.01, 3.282828... are all rational numbers.
In blackboard bold:
Irrational numbers
editIf a number can't be represented exactly by a fraction p/q, it is said to be irrational.
- Examples include: √2, √3, π.
Set Theory Exercise 1
editClick the link for Set Theory Exercise 1
Relationships between Sets
editWe’ll now look at various ways in which sets may be related to one another.
Equality
editTwo sets and are said to be equal if and only if they have exactly the same elements. In this case, we simply write:
Note two further facts about equal sets:
- The order in which elements are listed does not matter.
- If an element is listed more than once, any repeat occurrences are ignored.
So, for example, the following sets are all equal:
(You may wonder why one would ever come to write a set like . You may recall that when we defined the empty set we noted that there may be no solutions to a particular problem - hence the need for an empty set. Well, here we may be trying several different approaches to solving a problem, some of which in fact lead us to the same solution. When we come to consider the distinct solutions, however, any such repetitions would be ignored.)
Subsets
editIf all the elements of a set are also elements of a set , then we say that is a subset of and we write:
For example:
In the examples below:
If and , then If and , then If and , then
Notice that does not imply that must necessarily contain extra elements that are not in ; the two sets could be equal – as indeed and are above. However, if, in addition, does contain at least one element that isn’t in , then we say that is a proper subset of . In such a case we would write:
In the examples above:
contains ... -4, -2, 0, 2, 4, 6, 8, 10, 12, 14, ... , so
contains $, ;, &, ..., so
But and are just different ways of saying the same thing, so
The use of and ; is clearly analogous to the use of < and ≤ when comparing two numbers.
Notice also that every set is a subset of the universal set, and the empty set is a subset of every set.
(You might be curious about this last statement: how can the empty set be a subset of anything, when it doesn’t contain any elements? The point here is that for every set , the empty set doesn’t contain any elements that aren't in . So for all sets .)
Finally, note that if and must contain exactly the same elements, and are therefore equal. In other words:
Disjoint
editTwo sets are said to be disjoint if they have no elements in common. For example:
If and , then and are disjoint sets
Venn Diagrams
editA Venn diagram can be a useful way of illustrating relationships between sets.
In a Venn diagram:
- The universal set is represented by a rectangle. Points inside the rectangle represent elements that are in the universal set; points outside represent things not in the universal set. You can think of this rectangle, then, as a 'fence' keeping unwanted things out - and concentrating our attention on the things we're talking about.
- Other sets are represented by loops, usually oval or circular in shape, drawn inside the rectangle. Again, points inside a given loop represent elements in the set it represents; points outside represent things not in the set.


On the left, the sets A and B are disjoint, because the loops don't overlap.
On the right A is a subset of B, because the loop representing set A is entirely enclosed by loop B.
Venn diagrams: Worked Examples
edit
Example 1
Fig. 3 represents a Venn diagram showing two sets A and B, in the general case where nothing is known about any relationships between the sets.
Note that the rectangle representing the universal set is divided into four regions, labelled i, ii, iii and iv.
What can be said about the sets A and B if it turns out that:
- (a) region ii is empty?
- (b) region iii is empty?
(a) If region ii is empty, then A contains no elements that are not in B. So A is a subset of B, and the diagram should be re-drawn like Fig 2 above.
(b) If region iii is empty, then A and B have no elements in common and are therefore disjoint. The diagram should then be re-drawn like Fig 1 above.
Example 2
- (a) Draw a Venn diagram to represent three sets A, B and C, in the general case where nothing is known about possible relationships between the sets.
- (b) Into how many regions is the rectangle representing U divided now?
- (c) Discuss the relationships between the sets A, B and C, when various combinations of these regions are empty.
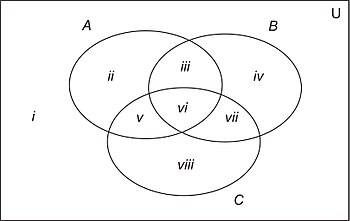
(a) The diagram in Fig. 4 shows the general case of three sets where nothing is known about any possible relationships between them.
(b) The rectangle representing U is now divided into 8 regions, indicated by the Roman numerals i to viii.
(c) Various combinations of empty regions are possible. In each case, the Venn diagram can be re-drawn so that empty regions are no longer included. For example:
- If region ii is empty, the loop representing A should be made smaller, and moved inside B and C to eliminate region ii.
- If regions ii, iii and iv are empty, make A and B smaller, and move them so that they are both inside C (thus eliminating all three of these regions), but do so in such a way that they still overlap each other (thus retaining region vi).
- If regions iii and vi are empty, 'pull apart' loops A and B to eliminate these regions, but keep each loop overlapping loop C.
- ...and so on. Drawing Venn diagrams for each of the above examples is left as an exercise for the reader.
Example 3
The following sets are defined:
- U = {1, 2, 3, …, 10}
- A = {2, 3, 7, 8, 9}
- B = {2, 8}
- C = {4, 6, 7, 10}
Using the two-stage technique described below, draw a Venn diagram to represent these sets, marking all the elements in the appropriate regions.
The technique is as follows:
- Draw a 'general' 3-set Venn diagram, like the one in Example 2.
- Go through the elements of the universal set one at a time, once only, entering each one into the appropriate region of the diagram.
- Re-draw the diagram, if necessary, moving loops inside one another or apart to eliminate any empty regions.
Don't begin by entering the elements of set A, then set B, then C – you'll risk missing elements out or including them twice!
Solution
After drawing the three empty loops in a diagram looking like Fig. 4 (but without the Roman numerals!), go through each of the ten elements in U - the numbers 1 to 10 - asking each one three questions; like this:
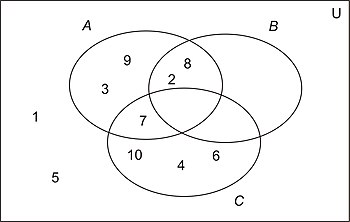
First element: 1
- Are you in A? No
- Are you in B? No
- Are you in C? No
A 'no' to all three questions means that the number 1 is outside all three loops. So write it in the appropriate region (region number i in Fig. 4).
Second element: 2
- Are you in A? Yes
- Are you in B? Yes
- Are you in C? No
Yes, yes, no: so the number 2 is inside A and B but outside C. Goes in region iii then.
...and so on, with elements 3 to 10.
The resulting diagram looks like Fig. 5.

The final stage is to examine the diagram for empty regions - in this case the regions we called iv, vi and vii in Fig. 4 - and then re-draw the diagram to eliminate these regions. When we've done so, we shall clearly see the relationships between the three sets.
So we need to:
- pull B and C apart, since they don't have any elements in common.
- push B inside A since it doesn't have any elements outside A.
The finished result is shown in Fig. 6.
The regions in a Venn Diagram and Truth Tables
editPerhaps you've realized that adding an additional set to a Venn diagram doubles the number of regions into which the rectangle representing the universal set is divided. This gives us a very simple pattern, as follows:
- With one set loop, there will be just two regions: the inside of the loop and its outside.
- With two set loops, there'll be four regions.
- With three loops, there'll be eight regions.
- ...and so on.
It's not hard to see why this should be so. Each new loop we add to the diagram divides each existing region into two, thus doubling the number of regions altogether.
| In A? | In B? | In C? |
|---|---|---|
| Y | Y | Y |
| Y | Y | N |
| Y | N | Y |
| Y | N | N |
| N | Y | Y |
| N | Y | N |
| N | N | Y |
| N | N | N |
But there's another way of looking at this, and it's this. In the solution to Example 3 above, we asked three questions of each element: Are you in A? Are you in B? and Are you in C? Now there are obviously two possible answers to each of these questions: yes and no. When we combine the answers to three questions like this, one after the other, there are then 23 = 8 possible sets of answers altogether. Each of these eight possible combinations of answers corresponds to a different region on the Venn diagram.
The complete set of answers resembles very closely a Truth Table - an important concept in Logic, which deals with statements which may be true or false. The table on the right shows the eight possible combinations of answers for 3 sets A, B and C.
You'll find it helpful to study the patterns of Y's and N's in each column.
- As you read down column C, the letter changes on every row: Y, N, Y, N, Y, N, Y, N
- Reading down column B, the letters change on every other row: Y, Y, N, N, Y, Y, N, N
- Reading down column A, the letters change every four rows: Y, Y, Y, Y, N, N, N, N
Set Theory Exercise 2
editClick link for Set Theory Exercise 2
Operations on Sets
editJust as we can combine two numbers to form a third number, with operations like 'add', 'subtract', 'multiply' and 'divide', so we can combine two sets to form a third set in various ways. We'll begin by looking again at the Venn diagram which shows two sets A and B in a general position, where we don't have any information about how they may be related.

| In A? | In B? | Region |
|---|---|---|
| Y | Y | iii |
| Y | N | ii |
| N | Y | iv |
| N | N | i |
The first two columns in the table on the right show the four sets of possible answers to the questions Are you in A? and Are you in B? for two sets A and B; the Roman numerals in the third column show the corresponding region in the Venn diagram in Fig. 7.
Intersection
editRegion iii, where the two loops overlap (the region corresponding to 'Y' followed by 'Y'), is called the intersection of the sets A and B. It is denoted by A ∩ B. So we can define intersection as follows:
- The intersection of two sets A and B, written A ∩ B, is the set of elements that are in A and in B.
(Note that in symbolic logic, a similar symbol, , is used to connect two logical propositions with the AND operator.)
For example, if A = {1, 2, 3, 4} and B = {2, 4, 6, 8}, then A ∩ B = {2, 4}.
We can say, then, that we have combined two sets to form a third set using the operation of intersection.
Union
editIn a similar way we can define the union of two sets as follows:
- The union of two sets A and B, written A ∪ B, is the set of elements that are in A or in B (or both).
The union, then, is represented by regions ii, iii and iv in Fig. 7.
(Again, in logic a similar symbol, , is used to connect two propositions with the OR operator.)
- So, for example, {1, 2, 3, 4} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 6, 8}.
You'll see, then, that in order to get into the intersection, an element must answer 'Yes' to both questions, whereas to get into the union, either answer may be 'Yes'.
The ∪ symbol looks like the first letter of 'Union' and like a cup that will hold a lot of items. The ∩ symbol looks like a spilled cup that won't hold a lot of items, or possibly the letter 'n', for i'n'tersection. Take care not to confuse the two.
Difference
edit- The difference of two sets A and B (also known as the set-theoretic difference of A and B, or the relative complement of B in A) is the set of elements that are in A but not in B.
This is written A - B, or sometimes A \ B.
The elements in the difference, then, are the ones that answer 'Yes' to the first question Are you in A?, but 'No' to the second Are you in B?. This combination of answers is on row 2 of the above table, and corresponds to region ii in Fig.7.
- For example, if A = {1, 2, 3, 4} and B = {2, 4, 6, 8}, then A - B = {1, 3}.
Complement
editSo far, we have considered operations in which two sets combine to form a third: binary operations. Now we look at a unary operation - one that involves just one set.
- The set of elements that are not in a set A is called the complement of A. It is written A′ (or sometimes AC, or ).
Clearly, this is the set of elements that answer 'No' to the question Are you in A?.
- For example, if U = N and A = {odd numbers}, then A′ = {even numbers}.
Notice the spelling of the word complement: its literal meaning is 'a complementary item or items'; in other words, 'that which completes'. So if we already have the elements of A, the complement of A is the set that completes the universal set.
Properties of set operations
edit1. Commutative
edit2. Associative
edit3. Distributive
edit4. Special properties of complements
edit5. De Morgan's Law
edit- .
Summary
edit
Cardinality
editFinally, in this section on Set Operations we look at an operation on a set that yields not another set, but an integer.
- The cardinality of a finite set A, written | A | (sometimes #(A) or n(A)), is the number of (distinct) elements in A. So, for example:
- If A = {lower case letters of the alphabet}, | A | = 26.
Generalized set operations
editIf we want to denote the intersection or union of n sets, A1, A2, ..., An (where we may not know the value of n) then the following generalized set notation may be useful:
- A1 ∩ A2 ∩ ... ∩ An = Ai
- A1 ∪ A2 ∪ ... ∪ An = Ai
In the symbol Ai, then, i is a variable that takes values from 1 to n, to indicate the repeated intersection of all the sets A1 to An.
Set Theory Exercise 3
editClick link for Set Theory Exercise 3
Set Theory Page 2
editPower Sets
editThe power set of a set A is the set of all its subsets (including, of course, itself and the empty set). It is denoted by P(A).
Using set comprehension notation, P(A) can be defined as
- P(A) = { Q | Q ⊆ A }
Example 4
- Write down the power sets of A if:
(a) A = {1, 2, 3}
(b) A = {1, 2}
(c) A = {1}
(d) A = ø
Solution
(a) P(A) = { {1, 2, 3}, {2, 3}, {1, 3}, {1, 2}, {1}, {2}, {3}, ø }
(b) P(A) = { {1, 2}, {1}, {2}, ø }
(c) P(A) = { {1}, ø }
(d) P(A) = { ø }
Cardinality of a Power Set
editLook at the cardinality of the four sets in Example 4, and the cardinality of their corresponding power sets. They are:
| | A | | | P(A) | | |
| (a) | 3 | 8 |
| (b) | 2 | 4 |
| (c) | 1 | 2 |
| (d) | 0 | 1 |
Clearly, there's a simple rule at work here: expressed as powers of 2, the cardinalities of the power sets are 23, 22, 21 and 20.
It looks as though we have found a rule that if | A | = k, then | P(A) | = 2k. But can we see why?
Well, the elements of the power set of A are all the possible subsets of A. Any one of these subsets can be formed in the following way:
- Choose any element of A. We may decide to include this in our subset, or we may omit it. There are therefore 2 ways of dealing with this first element of A.
- Now choose a second element of A. As before, we may include it, or omit it from our subset: again a choice of 2 ways of dealing with this element.
- ...and so on through all k elements of A.
Now the fundamental principle of combinatorics tells us that if we can do each of k things in 2 ways, then the total number of ways of doing them all, one after the other, is 2k.
Each one of these 2k combinations of decisions - including elements or omitting them - gives us a different subset of A. There are therefore 2k different subsets altogether.
So if | A | = k, then | P(A) | = 2k.
The Foundational Rules of Set Theory
editThe laws listed below can be described as the Foundational Rules of Set Theory. We derive them by going back to the definitions of intersection, union, universal set and empty set, and by considering whether a given element is in, or not in, one or more sets.
The Idempotent Laws
As an example, we'll consider the ′I heard you the first time′ Laws – more correctly called the Idempotent Laws - which say that:
- A ∩ A = A and A ∪ A = A
This law might be familiar to you if you've studied logic. The above relationship is comparable to the tautology.
These look pretty obvious, don't they? A simple explanation for the intersection part of these laws goes something like this:
The intersection of two sets A and B is defined as just those elements that are in A and in B. If we replace B by A in this definition we get that the intersection of A and A is the set comprising just those elements that are in A and in A. Obviously, we don't need to say this twice (I heard you the first time), so we can simply say that the intersection of A and A is the set of elements in A. In other words:
- A ∩ A = A
We can derive the explanation for A ∪ A = A in a similar way.
De Morgan's Laws
There are two laws, called De Morgan's Laws, which tell us how to remove brackets, when there's a complement symbol - ′ - outside. One of these laws looks like this:
- (A ∪ B) ′ = A ′ ∩ B ′
(If you've done Exercise 3, question 4, you may have spotted this law already from the Venn Diagrams.)
Look closely at how this Law works. The complement symbol after the bracket affects all three symbols inside the bracket when the brackets are removed:
- A becomes A ′
- B becomes B ′
- and ∪ becomes ∩.
To prove this law, note first of all that when we defined a subset we said that if
- A ⊆ B and B ⊆ A, then A = B
So we prove:
- (i) (A ∪ B) ′ ⊆ A ′ ∩ B ′
and then the other way round:
- (ii) A ′ ∩ B ′ ⊆ (A ∪ B) ′
The proof of (i) goes like this:
Let's pick an element at random x ∈ (A ∪ B) ′. We don't know anything about x; it could be a number, a function, or indeed an elephant. All we do know about x, is that
- x ∈ (A ∪ B) ′
So
- x ∉ (A ∪ B)
because that's what complement means.
This means that x answers No to both questions Are you in A? and Are you in B? (otherwise it would be in the union of A and B). Therefore
- x ∉ A and x ∉ B
Applying complements again we get
- x ∈ A ′ and x ∈ B ′
Finally, if something is in two sets, it must be in their intersection, so
- x ∈ A ′ ∩ B ′
So, any element we pick at random from (A ∪ B) ′ is definitely in A ′ ∩ B ′. So by definition
- (A ∪ B) ′ ⊆ A ′ ∩ B ′
The proof of (ii) is similar:
First, we pick an element at random from the first set, x ∈ A ′ ∩ B ′
Using what we know about intersections, that means
- x ∈ A ′ and x ∈ B ′
So, using what we know about complements,
- x ∉ A and x ∉ B
And if something is in neither A nor B, it can't be in their union, so
- x ∉ A ∪ B
So, finally:
- x ∈ (A ∪ B) ′
So:
- A ′ ∩ B ′ ⊆ (A ∪ B) ′
We've now proved (i) and (ii), and therefore:
- (A ∪ B) ′ = A ′ ∩ B ′
This gives you a taste for what's behind these laws. So here they all are.
The Laws of Sets
editCommutative Laws
- A ∩ B = B ∩ A
- A ∪ B = B ∪ A
Associative Laws
- (A ∩ B) ∩ C = A ∩ (B ∩ C)
- (A ∪ B) ∪ C = A ∪ (B ∪ C)
Distributive Laws
- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
- A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Idempotent Laws
- A ∩ A = A
- A ∪ A = A
Identity Laws
- A ∪ ø = A
- A ∩ U = A
- A ∪ U = U
- A ∩ ø = ø
Involution Law
(A ′) ′ = A
Complement Laws
- A ∪ A' = U
- A ∩ A' = ø
- U ′ = ø
- ø ′ = U
De Morgan’s Laws
- (A ∩ B) ′ = A ′ ∪ B ′
- (A ∪ B) ′ = A ′ ∩ B ′
Duality and Boolean Algebra
editYou may notice that the above Laws of Sets occur in pairs: if in any given law, you exchange ∪ for ∩ and vice versa (and, if necessary, swap U and ø) you get another of the laws. The 'partner laws' in each pair are called duals, each law being the dual of the other.
- For example, each of De Morgan's Laws is the dual of the other.
- The first complement law, A ∪ A ′ = U, is the dual of the second: A ∩ A ′ = ø.
- ... and so on.
This is called the Principle of Duality. In practical terms, it means that you only need to remember half of this table!
This set of laws constitutes the axioms of a Boolean Algebra. See Boolean Algebra for more.
Proofs using the Laws of Sets
editWe may use these laws - and only these laws - to determine whether other statements about the relationships between sets are true or false. Venn diagrams may be helpful in suggesting such relationships, but only a proof based on these laws will be accepted by mathematicians as rigorous.
Example 5
Using the Laws of Sets, prove that the set (A ∪ B) ∩ (A ′ ∩ B) ′ is simply the same as the set A itself. State carefully which Law you are using at each stage.
Before we begin the proof, a few do's and don't’s:
| Do start with the single expression (A ∪ B) ∩ (A ′ ∩ B) ′, and aim to change it into simply A. | Don’t begin by writing down the whole equation (A ∪ B) ∩ (A ′ ∩ B) ′ = A – that’s what we must end up with. |
| Do change just one part of the expression at a time, using just one of the set laws at a time. | Don't miss steps out, and change two things at once. |
| Do keep the equals signs underneath one another. | Don't allow your work to become untidy and poorly laid out. |
| Do state which law you have used at each stage. | Don't take even the simplest step for granted. |
Solution
| Law Used | ||
| (A ∪ B) ∩ (A ′ ∩ B) ′ | = (A ∪ B) ∩ ((A ′) ′ ∪ B ′) | De Morgan’s |
| = (A ∪ B) ∩ (A ∪ B ′) | Involution | |
| = A ∪ (B ∩ B ′) | Distributive | |
| = A ∪ ø | Complement | |
| = A | Identity |
We have now proved that (A ∪ B) ∩ (A ′ ∩ B) ′ = A whatever the sets A and B contain. A statement like this – one that is true for all values of A and B – is sometimes called an identity.
Hints on Proofs
There are no foolproof methods with these proofs – practice is the best guide. But here are a few general hints.
- Start with the more complicated side of the equation, aiming to simplify it into the other side.
- Look for places where the Distributive Law will result in a simplification (like factorising in 'ordinary' algebra - see the third line in Example 5 above).
- You’ll probably use De Morgan’s Law to get rid of a ' symbol from outside a bracket.
- Sometimes you may need to 'complicate' an expression before you can simplify it, as the next example shows.
Example 6
Use the Laws of Sets to prove that A ∪ (A ∩ B) = A.
Looks easy, doesn’t it? But you can go round in circles with this one. (Try it first before reading the solution below, if you like.) The key is to 'complicate' it a bit first, by writing the first A as A ∩ U (using one of the Identity Laws).
Solution
| Law Used | ||
| A ∪ (A ∩ B) | = (A ∩ U) ∪ (A ∩ B) | Identity |
| = A ∩ (U ∪ B) | Distributive | |
| = A ∩ (B ∪ U) | Commutative | |
| = A ∩ U | Identity | |
| = A | Identity |
Set Theory Exercise 4
editClick link for Set Theory Exercise 4.
Cartesian Products
editOrdered pair
editTo introduce this topic, we look first at a couple of examples that use the principle of combinatorics that we noted earlier (see Cardinality); namely, that if an event R can occur in r ways and a second event S can then occur in s ways, then the total number of ways that the two events, R followed by S, can occur is r × s. This is sometimes called the r-s Principle.
Example 7
| MENU |
| Main Course |
| Poached Halibut |
| Roast Lamb |
| Vegetable Curry |
| Lasagne |
| Dessert |
| Fresh Fruit Salad |
| Apple Pie |
| Gateau |
How many different meals – Main Course followed by Dessert - can be chosen from the above menu?
Solution
Since we may choose the main course in four ways, and then the dessert in three ways to form a different combination each time, the answer, using the r-s Principle, is that there are 4 × 3 = 12 different meals.
Example 8
You're getting ready to go out. You have 5 different (clean!) pairs of underpants and two pairs of jeans to choose from. In how many ways can you choose to put on a pair of pants and some jeans?
Solution
Using the r-s Principle, there are 5 × 2 = 10 ways in which the two can be chosen, one after the other.
In each of the two situations above, we have examples of ordered pairs. As the name says, an ordered pair is simply a pair of 'things' arranged in a certain order. Often the order in which the things are chosen is arbitrary – we simply have to decide on a convention, and then stick to it; sometimes the order really only works one way round.
In the case of the meals, most people choose to eat their main course first, and then dessert. In the clothes we wear, we put on our underpants before our jeans. You are perfectly free to fly in the face of convention and have your dessert before the main course - or to wear your underwear on top of your trousers - but you'll end up with different sets of ordered pairs if you do. And, of course, you'll usually have a lot of explaining to do!
The two 'things' that make up an ordered pair are written in round brackets, and separated by a comma; like this:
- (Lasagne, Gateau)
You will have met ordered pairs before if you've done coordinate geometry. For example, (2, 3) represents the point 2 units along the x-axis and 3 units up the y-axis. Here again, there's a convention at work in the order of the numbers: we use alphabetical order and put the x-coordinate before the y-coordinate. (Again, you could choose to do your coordinate geometry the other way round, and put y before x, but once again, you'd have a lot of explaining to do!)
Using set notation, then, we could describe the situation in Example 7 like this:
- M = {main courses}, D = {desserts}, C = {complete meals}.
Then C could be written as:
- C = { (m, d) | m ∈ M and d ∈ D }.
C is called the set product or Cartesian product of M and D, and we write:
- C = M × D
(read 'C equals M cross D')
Suppose that the menu in Example 7 is expanded to include a starter, which is either soup or fruit juice. How many complete meals can be chosen now?
Well, we can extend the r-s Principle to include this third choice, and get 2 × 4 × 3 = 24 possible meals.
If S = {soup, fruit juice}, then we can write:
- C = S × M × D
An element of this set is an ordered triple: (starter, main course, dessert). Notice, then, that the order in which the individual items occur in the triple is the same as the order of the sets from which they are chosen: S × M × D does not give us the same set of ordered triples as M × D × S.
Ordered n-tuples
editIn general, if we have n sets: A1, A2, ..., An, then their Cartesian product is defined by:
- A1 × A2 × ... × An = { (a1, a2, ..., an) | a1 ∈ A1, a2 ∈ A2, ..., an ∈ An) }
and (a1, a2, ..., an) is called an ordered n-tuple.
Notation
A1 × A2 × ... × An is sometimes written:
- Ai
The Cartesian Plane
edit
You probably know already the way in which a point in a plane may be represented by an ordered pair. The diagram in Fig. 8 illustrates a Cartesian Plane, showing the point represented by the ordered pair (5, 2).
The lines are called axes: the x-axis and the y-axis. The point where they meet is called the origin. The point (5, 2) is then located as follows: start at the origin; move 5 units in the direction of the x-axis, and then 2 units in the direction of the y-axis.
Using set notation:
If X = {numbers on the x-axis} and Y = {numbers on the y-axis}, then:
- (5, 2) ∈ X × Y
and, indeed, if X = {all real numbers}, and Y = {all real numbers} then X × Y as a whole represents all the points in the x-y plane.
(This is why you will sometimes see the x-y plane referred to as R2, where R = {real numbers}.)
Example 9
It is believed that, if A, B, P and Q are sets where B ⊂ A and Q ⊂ P, then:
- B × Q ⊂ A × P
Use a carefully shaded and labelled Cartesian diagram to investigate this proposition.
Solution
Bearing in mind what we said above about the ordered pairs in X × Y corresponding to points in the x-y plane, if we want to represent a Cartesian product like A × P on a diagram, we shall need to represent the individual sets A and P as sets of points on the x- and y- axes respectively.
The region representing the Cartesian product A × P is then represented by the points whose x- and y-coordinates lie within these sets A and P. Like this:

The same can also be said about B and Q: B must lie on the x-axis, and Q on the y-axis.
In addition, since B ⊂ A, then we must represent B as a set chosen from within the elements of A. Similarly, since Q ⊂ P, the elements of Q must lie within the elements of P.
When we add these components on to the diagram it looks like this:
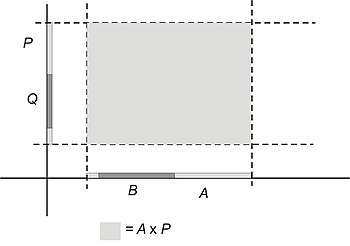
Finally, when we represent the set B × Q as a rectangle whose limits are determined by the limits of B and Q, it is clear that this rectangle will lie within the rectangle representing A × P:

So, the proposition B × Q ⊂ A × P appears to be true.
Set Theory Exercise 5
editClick link for Set Theory Exercise 5.
Functions and relations
editIntroduction
editThis article examines the concepts of a function and a relation.
A relation is any association or link between elements of one set, called the domain or (less formally) the set of inputs, and another set, called the range or set of outputs. Some people mistakenly refer to the range as the codomain(range), but as we will see, that really means the set of all possible outputs—even values that the relation does not actually use. (Beware: some authors do not use the term codomain(range), and use the term range instead for this purpose. Those authors use the term image for what we are calling range. So while it is a mistake to refer to the range or image as the codomain(range), it is not necessarily a mistake to refer to codomain as range.)
For example, if the domain is a set Fruits = {apples, oranges, bananas} and the codomain(range) is a set Flavors = {sweetness, tartness, bitterness}, the flavors of these fruits form a relation: we might say that apples are related to (or associated with) both sweetness and tartness, while oranges are related to tartness only and bananas to sweetness only. (We might disagree somewhat, but that is irrelevant to the topic of this book.) Notice that "bitterness", although it is one of the possible Flavors (codomain)(range), is not really used for any of these relationships; so it is not part of the range (or image) {sweetness, tartness}.
Another way of looking at this is to say that a relation is a subset of ordered pairs drawn from the set of all possible ordered pairs (of elements of two other sets, which we normally refer to as the Cartesian product of those sets). Formally, R is a relation if
for the domain X and codomain(range) Y. The inverse relation of R, which is written as R-1, is what we get when we interchange the X and Y values:
Using the example above, we can write the relation in set notation: {(apples, sweetness), (apples, tartness), (oranges, tartness), (bananas, sweetness)}. The inverse relation, which we could describe as "fruits of a given flavor", is {(sweetness, apples), (sweetness, bananas), (tartness, apples), (tartness, oranges)}. (Here, as elsewhere, the order of elements in a set has no significance.)
One important kind of relation is the function. A function is a relation that has exactly one output for every possible input in the domain. (The domain does not necessarily have to include all possible objects of a given type. In fact, we sometimes intentionally use a restricted domain in order to satisfy some desirable property.) The relations discussed above (flavors of fruits and fruits of a given flavor) are not functions: the first has two possible outputs for the input "apples" (sweetness and tartness); and the second has two outputs for both "sweetness" (apples and bananas) and "tartness" (apples and oranges).
The main reason for not allowing multiple outputs with the same input is that it lets us apply the same function to different forms of the same thing without changing their equivalence. That is, if f is a function with a (or b) in its domain, then a = b implies that f(a) = f(b). For example, z - 3 = 5 implies that z = 8 because f(x) = x + 3 is a function unambiguously defined for all numbers x.
The converse, that f(a) = f(b) implies a = b, is not always true. When it is, there is never more than one input x for a certain output y = f(x). This is the same as the definition of function, but with the roles of X and Y interchanged; so it means the inverse relation f-1 must also be a function. In general—regardless of whether or not the original relation was a function—the inverse relation will sometimes be a function, and sometimes not.
When f and f-1 are both functions, they are called one-to-one, injective, or invertible functions. This is one of two very important properties a function f might (or might not) have; the other property is called onto or surjective, which means, for any y ∈ Y (in the codomain), there is some x ∈ X (in the domain) such that f(x) = y. In other words, a surjective function f maps onto every possible output at least once.
A function can be neither one-to-one nor onto, both one-to-one and onto (in which case it is also called bijective or a one-to-one correspondence), or just one and not the other. (As an example which is neither, consider f = {(0,2), (1,2)}. It is a function, since there is only one y value for each x value; but there is more than one input x for the output y = 2; and it clearly does not "map onto" all integers.)
Relations
editIn the above section dealing with functions and their properties, we noted the important property that all functions must have, namely that if a function does map a value from its domain to its co-domain, it must map this value to only one value in the co-domain.
Writing in set notation, if a is some fixed value:
- |{f(x)|x=a}| ∈ {0, 1}
The literal reading of this statement is: the cardinality (number of elements) of the set of all values f(x), such that x=a for some fixed value a, is an element of the set {0, 1}. In other words, the number of outputs that a function f may have at any fixed input a is either zero (in which case it is undefined at that input) or one (in which case the output is unique).
However, when we consider the relation, we relax this constriction, and so a relation may map one value to more than one other value. In general, a relation is any subset of the Cartesian product of its domain and co-domain.
All functions, then, can be considered as relations also.
Notations
editWhen we have the property that one value is related to another, we call this relation a binary relation and we write it as
- x R y
where R is the relation.
For arrow diagrams and set notations, remember for relations we do not have the restriction that functions do and we can draw an arrow to represent the mappings, and for a set diagram, we need only write all the ordered pairs that the relation does take: again, by example
- f = {(0,0),(1,1),(-1,1),(2,2),(-2,2)}
is a relation and not a function, since both 1 and 2 are mapped to two values, (1 and -1, and 2 and -2 respectively) example let A=2,3,5;B=4,6,9 then A*B=(2,4),(2,6),(2,9),(3,4),(3,6),(3,9),(5,4),(5,6),(5,9) Define a relation R=(2,4),(2,6),(3,6),(3,9) add functions and problems to one another.
Some simple examples
editLet us examine some simple relations.
Say f is defined by
- {(0,0),(1,1),(2,2),(3,3),(1,2),(2,3),(3,1),(2,1),(3,2),(1,3)}
This is a relation (not a function) since we can observe that 1 maps to 2 and 3, for instance.
Less-than, "<", is a relation also. Many numbers can be less than some other fixed number, so it cannot be a function.
Properties
editWhen we are looking at relations, we can observe some special properties different relations can have.
Reflexive
editA relation is reflexive if, we observe that for all values a:
- a R a
In other words, all values are related to themselves.
The relation of equality, "=" is reflexive. Observe that for, say, all numbers a (the domain is R):
- a = a
so "=" is reflexive.
In a reflexive relation, we have arrows for all values in the domain pointing back to themselves:
Note that ≤ is also reflexive (a ≤ a for any a in R). On the other hand, the relation < is not (a < a is false for any a in R).
Symmetric
editA relation is symmetric if, we observe that for all values of a and b:
- a R b implies b R a
The relation of equality again is symmetric. If x=y, we can also write that y=x also.
In a symmetric relation, for each arrow we have also an opposite arrow, i.e. there is either no arrow between x and y, or an arrow points from x to y and an arrow back from y to x:
Neither ≤ nor < is symmetric (2 ≤ 3 and 2 < 3 but neither 3 ≤ 2 nor 3 < 2 is true).
Transitive
editA relation is transitive if for all values a, b, c:
- a R b and b R c implies a R c
The relation greater-than ">" is transitive. If x > y, and y > z, then it is true that x > z. This becomes clearer when we write down what is happening into words. x is greater than y and y is greater than z. So x is greater than both y and z.
The relation is-not-equal "≠" is not transitive. If x ≠ y and y ≠ z then we might have x = z or x ≠ z (for example 1 ≠ 2 and 2 ≠ 3 and 1 ≠ 3 but 0 ≠ 1 and 1 ≠ 0 and 0 = 0).
In the arrow diagram, every arrow between two values a and b, and b and c, has an arrow going straight from a to c.
Antisymmetric
editA relation is antisymmetric if we observe that for all values a and b:
- a R b and b R a implies that a=b
Notice that antisymmetric is not the same as "not symmetric."
Take the relation greater than or equal to, "≥" If x ≥ y, and y ≥ x, then y must be equal to x. a relation is anti-symmetric if and only if a∈A, (a,a)∈R
Trichotomy
editA relation satisfies trichotomy if we observe that for all values a and b it holds true that: aRb or bRa
The relation is-greater-or-equal satisfies since, given 2 real numbers a and b, it is true that whether a ≥ b or b ≥ a (both if a = b).
Problem set
editGiven the above information, determine which relations are reflexive, transitive, symmetric, or antisymmetric on the following - there may be more than one characteristic. (Answers follow.) x R y if
- x = y
- x < y
- x2 = y2
- x ≤ y
Answers
edit- Symmetric, Reflexive, and transitive
- Transitive, Trichotomy
- Symmetric, Reflexive, and transitive (x2 = y2 is just a special case of equality, so all properties that apply to x = y also apply to this case)
- Reflexive, Transitive and Antisymmetric (and satisfying Trichotomy)
Equivalence relations
editWe have seen that certain common relations such as "=", and congruence (which we will deal with in the next section) obey some of these rules above. The relations we will deal with are very important in discrete mathematics, and are known as equivalence relations. They essentially assert some kind of equality notion, or equivalence, hence the name.
Characteristics of equivalence relations
editFor a relation R to be an equivalence relation, it must have the following properties, viz. R must be:
- symmetric
- transitive
- reflexive
(A helpful mnemonic, S-T-R)
In the previous problem set you have shown equality, "=", to be reflexive, symmetric, and transitive. So "=" is an equivalence relation.
We denote an equivalence relation, in general, by .
Example proof
editSay we are asked to prove that "=" is an equivalence relation. We then proceed to prove each property above in turn (Often, the proof of transitivity is the hardest).
- Reflexive: Clearly, it is true that a = a for all values a. Therefore, = is reflexive.
- Symmetric: If a = b, it is also true that b = a. Therefore, = is symmetric
- Transitive: If a = b and b = c, this says that a is the same as b which in turn is the same as c. So a is then the same as c, so a = c, and thus = is transitive.
Thus = is an equivalence relation.
Partitions and equivalence classes
editIt is true that when we are dealing with relations, we may find that many values are related to one fixed value.
For example, when we look at the quality of congruence, which is that given some number a, a number congruent to a is one that has the same remainder or modulus when divided by some number n, as a, which we write
- a ≡ b (mod n)
and is the same as writing
- b = a+kn for some integer k.
(We will look into congruences in further detail later, but a simple examination or understanding of this idea will be interesting in its application to equivalence relations)
For example, 2 ≡ 0 (mod 2), since the remainder on dividing 2 by 2 is in fact 0, as is the remainder on dividing 0 by 2.
We can show that congruence is an equivalence relation (This is left as an exercise, below Hint use the equivalent form of congruence as described above).
However, what is more interesting is that we can group all numbers that are equivalent to each other.
With the relation congruence modulo 2 (which is using n=2, as above), or more formally:
- x ~ y if and only if x ≡ y (mod 2)
we can group all numbers that are equivalent to each other. Observe:
This first equation above tells us all the even numbers are equivalent to each other under ~, and all the odd numbers under ~.
We can write this in set notation. However, we have a special notation. We write:
- [0]={0,2,4,...}
- [1]={1,3,5,...}
and we call these two sets equivalence classes.
All elements in an equivalence class by definition are equivalent to each other, and thus note that we do not need to include [2], since 2 ~ 0.
We call the act of doing this 'grouping' with respect to some equivalence relation partitioning (or further and explicitly partitioning a set S into equivalence classes under a relation ~). Above, we have partitioned Z into equivalence classes [0] and [1], under the relation of congruence modulo 2.
Problem set
editGiven the above, answer the following questions on equivalence relations (Answers follow to even numbered questions)
- Prove that congruence is an equivalence relation as before (See hint above).
- Partition {x | 1 ≤ x ≤ 9} into equivalence classes under the equivalence relation
Answers
edit2. [0]={6}, [1]={1,7}, [2]={2,8}, [3]={3,9}, [4]={4}, [5]={5}
Partial orders
editWe also see that "≥" and "≤" obey some of the rules above. Are these special kinds of relations too, like equivalence relations? Yes, in fact, these relations are specific examples of another special kind of relation which we will describe in this section: the partial order.
As the name suggests, this relation gives some kind of ordering to numbers.
Characteristics of partial orders
editFor a relation R to be a partial order, it must have the following three properties, viz R must be:
- reflexive
- antisymmetric
- transitive
(A helpful mnemonic, R-A-T)
We denote a partial order, in general, by .
Question:
- Suppose R is a relation on a set of integers Z then prove that R is a partial order relation on Z iff a=b raise to power r.
Example proof
editSay we are asked to prove that "≤" is a partial order. We then proceed to prove each property above in turn (Often, the proof of transitivity is the hardest).
Reflexive
editClearly, it is true that a ≤ a for all values a. So ≤ is reflexive.
Antisymmetric
editIf a ≤ b, and b ≤ a, then a must be equal to b. So ≤ is antisymmetric
Transitive
editIf a ≤ b and b ≤ c, this says that a is less than b and c. So a is less than c, so a ≤ c, and thus ≤ is transitive.
Thus ≤ is a partial order.
Problem set
editGiven the above on partial orders, answer the following questions
- Prove that divisibility, |, is a partial order (a | b means that a is a factor of b, i.e., on dividing b by a, no remainder results).
- Prove the following set is a partial order: (a, b) (c, d) implies ab≤cd for a,b,c,d integers ranging from 0 to 5.
Answers
edit2. Simple proof; Formalization of the proof is an optional exercise.
- Reflexivity: (a, b) (a, b) since ab=ab.
- Antisymmetric: (a, b) (c, d) and (c, d) (a, b) since ab≤cd and cd≤ab imply ab=cd.
- Transitive: (a, b) (c, d) and (c, d) (e, f) implies (a, b) (e, f) since ab≤cd≤ef and thus ab≤ef
Posets
editA partial order imparts some kind of "ordering" amongst elements of a set. For example, we only know that 2 ≥ 1 because of the partial ordering ≥.
We call a set A, ordered under a general partial ordering , a partially ordered set, or simply just poset, and write it (A, ).
Terminology
editThere is some specific terminology that will help us understand and visualize the partial orders.
When we have a partial order , such that a b, we write to say that a but a ≠ b. We say in this instance that a precedes b, or a is a predecessor of b.
If (A, ) is a poset, we say that a is an immediate predecessor of b (or a immediately precedes b) if there is no x in A such that a x b.
If we have the same poset, and we also have a and b in A, then we say a and b are comparable if a b or b a. Otherwise they are incomparable.
Hasse diagrams
editHasse diagrams are special diagrams that enable us to visualize the structure of a partial ordering. They use some of the concepts in the previous section to draw the diagram.
A Hasse diagram of the poset (A, ) is constructed by
- placing elements of A as points
- if a and b ∈ A, and a is an immediate predecessor of b, we draw a line from a to b
- if a b, put the point for a lower than the point for b
- not drawing loops from a to a (this is assumed in a partial order because of reflexivity)
Operations on Relations
editThere are some useful operations one can perform on relations, which allow to express some of the above mentioned properties more briefly.
Inversion
editLet R be a relation, then its inversion, R-1 is defined by
R-1 := {(a,b) | (b,a) in R}.
Concatenation
editLet R be a relation between the sets A and B, S be a relation between B and C. We can concatenate these relations by defining
R • S := {(a,c) | (a,b) in R and (b,c) in S for some b out of B}
Diagonal of a Set
editLet A be a set, then we define the diagonal (D) of A by
D(A) := {(a,a) | a in A}
Shorter Notations
editUsing above definitions, one can say (lets assume R is a relation between A and B):
R is transitive if and only if R • R is a subset of R.
R is reflexive if and only if D(A) is a subset of R.
R is symmetric if R-1 is a subset of R.
R is antisymmetric if and only if the intersection of R and R-1 is D(A).
R is asymmetric if and only if the intersection of D(A) and R is empty.
R is a function if and only if R-1 • R is a subset of D(B).
In this case it is a function A → B. Let's assume R meets the condition of being a function, then
R is injective if R • R-1 is a subset of D(A).
R is surjective if {b | (a,b) in R} = B.
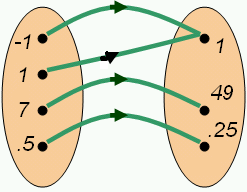
Functions
editA function is a relationship between two sets of numbers. We may think of this as a mapping; a function maps a number in one set to a number in another set. Notice that a function maps values to one and only one value. Two values in one set could map to one value, but one value must never map to two values: that would be a relation, not a function.
|
For example, if we write (define) a function as:
then we say:
- 'f of x equals x squared'
and we have
and so on.
This function f maps numbers to their squares.
Range and codomain
editIf D is a set, we can say
which forms a née of f is usually a subset of a larger set. This set is known as the codomain of a function. For example, with the function f(x)=cos x, the range of f is [-1,1], but the codomain is the set of real numbers.
Notations
editWhen we have a function f, with domain D and range R, we write:
If we say that, for instance, x is mapped to x2, we also can add
Notice that we can have a function that maps a point (x,y) to a real number, or some other function of two variables -- we have a set of ordered pairs as the domain. Recall from set theory that this is defined by the Cartesian product - if we wish to represent a set of all real-valued ordered pairs we can take the Cartesian product of the real numbers with itself to obtain
- .
When we have a set of n-tuples as part of the domain, we say that the function is n-ary (for numbers n=1,2 we say unary, and binary respectively).
Other function notation
editFunctions can be written as above, but we can also write them in two other ways. One way is to use an arrow diagram to represent the mappings between each element. We write the elements from the domain on one side, and the elements from the range on the other, and we draw arrows to show that an element from the domain is mapped to the range.
For example, for the function f(x)=x3, the arrow diagram for the domain {1,2,3} would be:
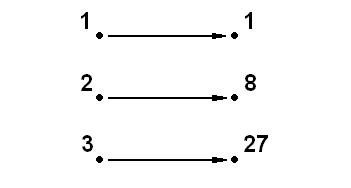
Another way is to use set notation. If f(x)=y, we can write the function in terms of its mappings. This idea is best to show in an example.
Let us take the domain D={1,2,3}, and f(x)=x2. Then, the range of f will be R={f(1),f(2),f(3)}={1,4,9}. Taking the Cartesian product of D and R we obtain F={(1,1),(2,4),(3,9)}.
So using set notation, a function can be expressed as the Cartesian product of its domain and range.
f(x)
This function is called f, and it takes a variable x. We substitute some value for x to get the second value, which is what the function maps x to.
Types of functions
editFunctions can either be one to one (injective), onto (surjective), or bijective.
INJECTIVE Functions are functions in which every element in the domain maps into a unique elements in the codomain.
SURJECTIVE Functions are functions in which every element in the codomain is mapped by an element in the domain.
'BIJECTIVE Functions are functions that are both injective and surjective.
---onto functions a function f form A to B is onto ,
Number theory
editIntroduction
edit'Number theory' is a large encompassing subject in its own right. Here we will examine the key concepts of number theory.
Unlike real analysis and calculus which deals with the dense set of real numbers, number theory examines mathematics in discrete sets, such as N or Z. If you are unsure about sets, you may wish to revisit Set theory.
Number Theory, the study of the integers, is one of the oldest and richest branches of mathematics. Its basic concepts are those of divisibility, prime numbers, and integer solutions to equations -- all very simple to understand, but immediately giving rise to some of the best known theorems and biggest unsolved problems in mathematics. The Theory of Numbers is also a very interdisciplinary subject. Ideas from combinatorics (the study of counting), algebra, and complex analysis all find their way in, and eventually become essential for understanding parts of number theory. Indeed, the greatest open problem in all mathematics, the Riemann Hypothesis, is deeply tied into Complex Analysis. But never fear, just start right into Elementary Number Theory, one of the warmest invitations to pure mathematics, and one of the most surprising areas of applied mathematics!
Divisibility
editNote that in R, Q, and C, we can divide freely, except by zero. This property is often known as closure -- the quotient of two rationals is again a rational, etc.. However, if we move to performing mathematics purely in a set such as Z, we come into difficulty. This is because, in the integers, the result of a division of two integers might not be another integer. For example, we can of course divide 6 by 2 to get 3, but we cannot divide 6 by 5, because the fraction 6/5 is not in the set of integers.
However we can introduce a new relation where division is defined. We call this relation divisibility, and if is an integer, we say:
- divides
- is a factor of
- is a multiple of
- is divisible by
Formally, if there exists an integer such that then we say that divides and write . If does not divide then we write :
Proposition. The following are basic consequences of this definition. Let a, b, and c be integers:
- (a) If a|b then a|(bc).
- (b) If a|b and b|c, then a|c.
- (c) If a|b and a|c, then for any integers x and y, a|(xb+yc) -- in other words a divides any linear combination of its multiples.
- (d) If both a|b and b|a, then a = b or a = -b.
- (e) If c is not 0, then a|b is equivalent to ca|cb.
Quotient and divisor theorem
editFor any integer n and any k > 0, there is a unique q and r such that:
- n = qk + r (with 0 ≤ r < k)
Here n is known as dividend.
We call q the quotient, r the remainder, and k the divisor.
It is probably easier to recognize this as division by the algebraic re-arrangement:
- n/k = q + r/k (0 ≤ r/k < 1)
Modular arithmetic
editWhat can we say about the numbers that divide another? Pick the number 8 for example. What is the remainder on dividing 1 by 8? Using the division theorem above
- 0 = 8*0 + 0
- 1 = 8*0 + 1
- 2 = 8*0 + 2
- :
- 8 = 8*1 + 0
- 9 = 8*1 + 1
- 10 = 8 * 1 + 2
- :
- and so on
We have a notation for the remainders, and can write the above equations as
- 0 mod 8 = 0
- 1 mod 8 = 1
- 2 mod 8 = 2
- 3 mod 8 = 3
- 4 mod 8 = 4
- 5 mod 8 = 5
- 6 mod 8 = 6
- 7 mod 8 = 7
- 8 mod 8 = 0
- 9 mod 8 = 1
- 10 mod 8 = 2
- :
We can also write
- 1 ≡ 1 (mod 8)
- 2 ≡ 2 (mod 8)
- 3 ≡ 3 (mod 8)
- 4 ≡ 4 (mod 8)
- 5 ≡ 5 (mod 8)
- 6 ≡ 6 (mod 8)
- 7 ≡ 7 (mod 8)
- 8 ≡ 0 (mod 8)
- 9 ≡ 1 (mod 8)
- 10 ≡ 2 (mod 8)
- :
These notations are all short for
- a = 8k+r for some integer k.
So x ≡ 1 (mod 8), for example, is the same as saying
- x = 8k+1
Observe that the remainder here, in comparing it with the division algorithm is 1. x ≡ 1 (mod 8) asks what numbers have the remainder 1 on division by 8? Clearly the solutions are x=8×0+1, 8×1+1,... = 1, 9, ...
Often the entire set of remainders on dividing by n - which we say modulo n - are interesting to look at. We write this set Zn. Note that this set is finite. The remainder on dividing 9 by 8 is 1 - the same as dividing 1 by 8. So in a sense 9 is really "the same as" 1. In fact, the relation "≡"
- x ≡ y iff x mod n = y mod n.
is an equivalence relation. We call this relation congruence. Note that the equivalence classes defined by congruence are precisely the elements of Zn.
We can find some number a modulo n (or we say a congruent to n) by finding its decomposition using the division algorithm.
Addition, subtraction, and multiplication work in Zn - for example 3 + 6 (mod 8) = 9 (mod 8) = 1 (mod 8). The numbers do look strange but they follow many normal properties such as commutativity and associativity.
If we have a number greater than n we often reduce it modulo n first - again using the division algorithm. For example if we want to find 11+3 mod 8, its often easier to calculate 3 + 3 (mod 8) rather than reducing 14 mod 8. A trick that's often used is that, say, if we have 6 + 7 (mod 8) we can use negative numbers instead so the problem becomes -2 + -1 = -3 = 5 (mod 8).
We often use the second notation when we want to look at equations involving numbers modulo some n. For example, we may want to find a number x such that
- 3x ≡ 5 (mod 8)
We can find solutions by trial substitution (going through all the numbers 0 through 7), but what if the moduli are very large? We will look at a more systematic solution later.
Note: we often say that we are working in Zn and use equals signs throughout. Familiarize yourself with the three ways of writing modular equations and expressions.
The Consistency of Modular Arithmetic
editLet denote an arbitrary base. Given an arbitrary integer , the sequence of integers are all congruent to each other modulo :
In modular arithmetic, two integers and that are congruent modulo () both "represent" the same quantity from . It should be possible to substitute an arbitrary integer in place of integer provided that .
This means that:
- Given arbitrary integers and , if and , then .
Since , there exists an integer such that .
Since , there exists an integer such that .
It can be derived that so therefore .
- Given arbitrary integers and , if and , then .
Since , there exists an integer such that .
Since , there exists an integer such that .
It can be derived that so therefore .
Number Bases
editConverting between various number bases is one of the most tedious processes in mathematics.
The numbers that are generally used in transactions are all in base-10. This means that there are 10 digits that are used to describe a number. These ten digits are {0,1,2,3,4,5,6,7,8,9}.
Similarly, base-4 has 4 digits {0,1,2,3} and base-2 has two digits {0,1}. Base two is sometimes referred to as Binary.
There are also bases greater than 10. For these bases, it is customary to use letters to represent digits greater than 10. An example is Base-16 (Hexadecimal). The digits used in this base are {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}.
In order to convert between number bases, it is critical that one knows how to divide numbers and find remainders.
To convert from decimal to another base one must simply start dividing by the value of the other base, then dividing the result of the first division and overlooking the remainder, and so on until the base is larger than the result (so the result of the division would be a zero). Then the number in the desired base is the remainders read from end to start.
The following shows how to convert a number (105) which is in base-10 into base-2.
| Operation | Remainder |
|---|---|
| 105 / 2 = 52 | 1 |
| 52 / 2 = 26 | 0 |
| 26 / 2 = 13 | 0 |
| 13 / 2 = 6 | 1 |
| 6 / 2 = 3 | 0 |
| 3 / 2 = 1 | 1 |
| 1 / 2 = 0 | 1 |
Answer : 1101001
After finishing this process, the remainders are taken and placed in a row (from bottom to top) after the final quotient (1101001, in this example) is shown as the base-2 equivalent of the number 105.
To sum up the process, simply take the original number in base 10, and divide that number repeatedly, keeping track of the remainders, until the quotient becomes less than the numerical value of the base.
This works when converting any number from base-10 to any base. If there are any letters in the base digits, then use the letters to replace any remainder greater than 9. For example, writing 11(of base-10) in base 14.
| Operation | Remainder |
|---|---|
| 11 / 14 = 0 | B (=11) |
Answer: B
As 11 is a single remainder, it is written as a single digit. Following the pattern {10=A, 11=B, 12=C...35=Z}, write it as B. If you were to write "11" as the answer, it would be wrong, as "11" Base-14 is equal to 15 in base-10!
In order to convert from a number in any base back to base ten, the following process should be used:
Take the number 3210 (in base-10). In the units place (100), there is a 0. In the tens place (101), there is a 1. In the hundreds place (102), there is a 2. In the thousands place (103), there is a 3.
The formula to find the value of the above number is:
3×103 + 2×102 + 1×101 + 0×100 = 3000 + 200 + 10 + 0 = 3210.
The process is similar when converting from any base to base-10. For example, take the number 3452 (in base-6). In the units place (60), there is a 2. In the sixths place (61) there is a 5. In the thirty-sixths place (62), there is a 4. In the 216th place (63), there is a 3.
The formula to find the value of the above number (in base-10) is:
3×63 + 4×62 + 5×61 + 2×60 = 648 + 144 + 30 + 2 = 824.
The value of 3452 (base-6) is 824 in base-10.
A more efficient algorithm is to add the left-most digit and multiply by the base, and repeat with the next digit and so on.
((3 * 6 + 4) * 6 + 5) * 6 + 2 = 824
The processes to convert between number bases may seem difficult at first, but become easy if one practices often.
Prime numbers
editPrime numbers are the building blocks of the integers. A prime number is a positive integer greater than one that has only two divisors: 1, and the number itself. For example, 17 is prime because the only positive integers that divide evenly into it are 1 and 17. The number 6 is not a prime since more than two divisors 1, 2, 3, 6 divide 6. Also, note that 1 is not a prime since 1 has only one divisor.
Some prime numbers
editThe prime numbers as a sequence begin
- 2, 3, 5, 7, 11, 13, 17, 19, 23, ...
Euclid's Proof that There are Infinitely Many Primes
editThe Greek mathematician Euclid gave the following elegant proof that there are an infinite number of primes. It relies on the fact that all non-prime numbers --- composites --- have a unique factorization into primes.
Euclid's proof works by contradiction: we will assume that there are a finite number of primes, and show that we can derive a logically contradictory fact.
So here we go. First, we assume that that there are a finite number of primes:
- p1, p2, ... , pn
Now consider the number M defined as follows:
- M = 1 + p1 * p2 * ... * pn
There are two important --- and ultimately contradictory --- facts about the number M:
- It cannot be prime because pn is the biggest prime (by our initial assumption), and M is clearly bigger than pn. Thus, there must be some prime p that divides M.
- It is not divisible by any of the numbers p1, p2, ..., pn. Consider what would happen if you tried to divide M by any of the primes in the list p1, p2, ... , pn. From the definition of M, you can tell that you would end up with a remainder of 1. That means that p --- the prime that divides M --- must be bigger than any of p1, ..., pn.
Thus, we have shown that M is divisible by a prime p that is not on the finite list of all prime. And so there must be an infinite number of primes.
These two facts imply that M must be divisible by a prime number bigger than pn. Thus, there cannot be a biggest prime.
Note that this proof does not provide us with a direct way to generate arbitrarily large primes, although it always generates a number which is divisible by a new prime. Suppose we know only one prime: 2. So, our list of primes is simply p1=2. Then, in the notation of the proof, M=1+2=3. We note that M is prime, so we add 3 to the list. Now, M = 1 +2 *3 = 7. Again, 7 is prime. So we add it to the list. Now, M = 1+2*3*7 = 43: again prime. Continuing in this way one more time, we calculate M = 1+2*3*7*43 = 1807 =13*139. So we see that M is not prime.
Viewed another way: note that while 1+2, 1+2*3, 1+2*3*5, 1+2*3*5*7, and 1+2*3*5*7*11 are prime, 1+2*3*5*7*11*13=30031=59*509 is not.
Testing for primality
editThere are a number of simple and sophisticated primality tests. We will consider some simple tests here. In upper-level courses we will consider some faster and more sophisticated methods to test whether a number is prime.
Inspection
editThe most immediate and simple test to eliminate a number n as a prime is to inspect the units digit or the last digit of a number.
If the number n ends in an even number 0, 2, 4, 6, 8 we can show that number n cannot be a prime. For example, take n = 87536 = 8753(10) + 6. Since 10 is divisible by 2 and 6 is divisible by 2 then 87536 must be divisible by 2. In general, any even number can be expressed in the form n = a*10 + b, where b = 0, 2, 4, 6, 8. Since 10 is divisible by 2 and b is divisible by 2 then n = a*10 + b is divisible by 2. Consequently, any number n which ends in an even number such as 7777732 or 8896 is divisible by 2 so n is not a prime.
In a similar type of argument, if a number n ends in a 5 we can show the number n cannot be a prime. If the last digit of n, call it b, is a 5 we can express n in the form n = a*10 + b, where b = 5. Since 10 is divisible by 5 and b = 5 is divisible by 5 then n = a*10 + b is divisible by 5. Hence, any number n which ends in a 5 such as 93475 is divisible by 5 so n is not a prime.
Thus, if a number greater than 5 is a prime it must end with either a 1, 3, 7, or 9. Note that this does not mean all numbers that end in a 1, 3, 7, or 9 are primes. For example, while the numbers 11, 23, 37, 59 are primes, the numbers 21 = 3*7, 33 = 3*11, 27 = 3*9, 39 = 3*13 are not primes. Consequently, if a number ends in a 1, 3, 7, or 9 we have to test further.
Trial Division Method
editTo test if a number n that ends in a 1, 3, 7, or 9 is prime, we could simply try the smallest prime number and try to divide it in n. If that doesn't divide, we would take the next largest prime number and try again etc. Certainly, if we took all primes numbers in this manner that were less than n and we could not divide n then we would be justified in saying n is prime. However, it can be shown that you don't have to take all primes smaller than n to test if n is prime. We can stop earlier by using the Trial Division Method.
The justification of the Trial Division Method is if a number n has no divisors less than or equal to then n must be a prime. We can show this by contradiction. Let us assume n has no divisors less than or equal to . If n is not a prime, there must be two numbers a and b such that . In particular, by our assumption and . But then . Since a number can not be greater than itself the number n must be a prime.
Trial Division Method is a method of primality testing that involves taking a number n and then sequentially dividing it by primes up to .
For example, is 113 prime? is approximately 10.63... We only need to test whether 2, 3, 5, 7 divide 113 cleanly (leave no remainder, i.e., the quotient is an integer).
- 113/2 is not an integer since the last digit is not even.
- 113/3 (=37.666...) is not an integer.
- 113/5 is not an integer since the last digit does not end in a 0 or 5.
- 113/7 (=16.142857...) is not an integer.
So we need not look at any more primes such as 11, 13, 17 etc. less than 113 to test, since 2, 3, 5, 7 does not divide 113 cleanly, 113 is prime.
Notice that after rejecting 2 and 3 as a divisor, we next considered the next prime number 5 and not the next number 4. We know not to consider 4 because we know 2 does not divide 113. If 2 cannot divide 113 then certainly 4 cannot because if 4 divided 113 and since 2 divides 4 then 2 would divide 113. So we only use the next cheapest available prime to test not the next consecutive number.
If we test 91 we get,
- 91/2 is not an integer since that last digit is not even.
- 91/3= (30.333) is not an integer.
- 91/5= is not an integer since the last digit does not end in a 0 or 5.
- 91/7=13 is an integer
So we know since 7 divides 91, 91 is not a prime.
Trial division is normally only used for relatively small numbers due to its inefficiency. However this technique has the two advantages that firstly once we have tested a number we know for sure that it is prime and secondly if a number is not prime it also gives us the number's factors.
To obtain a few small primes, it may be best to use the Sieve of Eratosthenes than to test each number sequentially using trial division. The Sieve of Eratosthenes method is basically a process of finding primes by elimination. We start by taking a list of consecutive numbers say 1 to 100. Cross out the number 1 because the number is not prime. Take the next least uncrossed off number which is 2 and circle it. Now cross out all multiples of 2 on the list. Next take the next least uncircled number which is 3. Circle the number 3 and cross out all multiples of 3. The next least uncircled number should be 5 since 4 is a multiple of 2 and should have been crossed off. Circle the number 5 and cross out all multiples of 5. The next least uncircled number should be a 7 since 6 is a multiple of 2. Circle the 7 and mark off all multiples of 7. Now the next uncrossed off number should be 11 since 8,9,10 is a multiple of 2, 3, and 2. If we continue in this manner what is left is the circled numbers which are primes. But notice we can actually stop now and circle all the unmarked numbers after crossing off multiples of 7 because of the result that since any number less than 100 which is not prime must be divisible by 2, 3, 5, or 7.
The Fundamental Theorem of Arithmetic
editThe Fundamental Theorem of Arithmetic is an important theorem relating to the factorization of numbers. The theorem basically states that every positive integer can be written as the product of prime numbers in a unique way (ignoring reordering the product of prime numbers).
In particular, The Fundamental Theorem of Arithmetic means any number such as 1,943,032,663 is either a prime or can be factored into a product of primes. If a number such as 1,943,032,663 can be factored into primes such as 11×13×17×19×23×31×59 it is futile to try to find another different combination of prime numbers that will also give you the same number.
To make the theorem work even for the number 1, we think of 1 as being the product of zero prime numbers.
More formally,
- For all n∈N
- n=p1p2p3...
- where the pi are all prime numbers, and can be repeated.
Here are some examples.
- 4 = 2 × 2 = 22
- 12 = 2 × 2 × 3 = 22 × 3
- 11 = 11.
A proof of the Fundamental Theorem of Arithmetic will be given after Bezout's identity has been established.
LCM and GCD
editTwo characteristics we can determine between two numbers based on their factorizations are the lowest common multiple, the LCM and greatest common divisor, the GCD (also greatest common factor, GCF)
LCM
editThe lowest common multiple, or the least common multiple, for two numbers a and b is the smallest number designated by LCM(a,b) that is divisible by both the number a and the number b. We can find LCM(a,b) by finding the prime factorization of a and b and choosing the maximum power for each prime factor.
In another words, if the number a factors to , and the number b factors to , then LCM(a,b) = where for i = 1 to n.
An example, let us see the process on how we find lowest common multiple for 5500 and 450 which happens to be 49500. First, we find the prime factorization for 5500 and 450 which is
- 5500=22 53 11
- 450=2 3 2 52
Notice the different primes we came up for both the number 5500 and the number 450 are 2, 3, 5, and 11. Now let us express 5500 and 450 completely in a product of these primes raised to the appropriate power.
- 5500=22 53 11 = 22 30 53 111
- 450=2 32 52 = 21 32 52 110
The LCM(5500,450) is going to be in the form 2? 3? 5? 11?. All we now have to do is find what the powers of each individual prime will be.
So now we compare the power of each prime for 5500 and 450. Let us consider the powers of the first prime 2. In the number 5500, the prime 2 is raised to the second power and in the number 450, prime 2 is raised to the first power. Since the maximum between 2 and 1 for the power of the prime 2 is 2, we use 2 for the power of the prime 2.
Now let us consider the powers of the prime 3. In the number 5500, the prime 3 is raised to the zero power and in the number 450 the prime 3 is raised to the second power. Since the maximum between 0 and 2 for the power of the prime 3 is 2, we use 2 for the power of the prime 3.
Similarly, let us consider the powers of the next prime 5. In the number 5500, the prime 5 is raised to the third power and in the number 450 the prime 5 is raised to the second power. Since the maximum between 3 and 2 for the power of the prime 5 is 3, we use 3 for the power of the prime 5.
Finally, let us consider the powers of the prime 11, the last prime on our list. In the number 5500, the prime 11 is raised to the first power and in the number 450 the prime 11 is raised to the zero power. Since the maximum between 1 and 0 for the power of the prime 11 is 1, we use 1 for the power of the last prime 11.
Consequently, the product of our results is LCM(5500,450)=22 32 53 111 = 49500.
GCD
editThe greatest common divisor for two numbers a and b is the biggest number designated by GCD(a,b) that divides both the number a and the number b. In a similar process to finding LCM(a,b), we can find GCD(a,b) by finding the prime factorization of a and b but choosing the minimum power for each prime factor instead.
In other words, if the number a factors to , and the number b factors to , then GCD(a,b) = where for i = 1 to n.
An example, let us see the process on how we find the greatest common divisor for 5500 and 450 which happens to be 50. First, we find the prime factorization for 5500 and 450 which is
- 5500=22 53 11
- 450=2 3 2 52
Notice the different primes we came up for both the number 5500 and the number 450 are 2, 3, 5, and 11. Now let us express 5500 and 450 completely in a product of these primes raised to the appropriate power.
- 5500=22 53 11 = 22 30 53 111
- 450=2 32 52 = 21 32 52 110
The GCD(5500,450) is going to be in the form 2? 3? 5? 11?. All we now have to do is find what the powers of each individual prime will be.
So now we compare the power of each prime for 5500 and 450. Let us consider the powers of the first prime 2. In the number 5500, the prime 2 is raised to the second power and in the number 4</syntaxhighlight> 50, prime 2 is raised to the first power. Since the minimum between 2 and 1 for the power of the prime 2 is 1, we use 1 for the power of the prime 2.
Now let us consider the powers of the prime 3. In the number 5500, the prime 3 is raised to the zero power and in the number 450 the prime 3 is raised to the second power. Since the minimum between 0 and 2 for the power of the prime 3 is 0, we use 0 for the power of the prime 3.
Similarly, let us consider the powers of the next prime 5. In the number 5500, the prime 5 is raised to the third power and in the number 450 the prime 5 is raised to the second power. Since the minimum between 3 and 2 for the power of the prime 5 is 2, we use 2 for the power of the prime 5.
Finally, let us consider the powers of the prime 11, the last prime on our list. In the number 5500, the prime 11 is raised to the first power and in the number 450 the prime 11 is raised to the zero power. Since the minimum between 1 and 0 for the power of the prime 11 is 0, we use 0 for the power of the last prime 11.
Consequently, the product of our results is GCD(5500,450)=21 30 52 110 = 50.
Properties
edit- gcd(a,b)=gcd(b,a)
- gcd(a,b) = gcd(b,q), where q is the remainder of a divided by b
- gcd(a/d, b/d)=1, where d is gcd(a,b)
The Euclidean algorithm
editThe Euclidean algorithm is such that we can find the gcd of two numbers without finding the factorization*. The Euclidean algorithm consists of only addition and multiplication, and uses the above properties of gcd as its basis.
* Factorization is a "hard" process, that is, to factor a number takes a long time depending on the length of the number. This is why later, when you need to find the gcd of a pair of numbers, you will most likely never factorize the numbers and use the properties of the primes but will use the Euclidean algorithm instead.
An example
editWe will see how this works by calculating gcd(458,44)
First, divide 458 by 44 and obtain the remainder:
- 458 = 44 × 10 + 18
Now suppose that a number is a common divisor of 458 and 44. Then it must also be a divisor of 18. To see this, rearrange the above equation to:
- 458 - 44×10 =18
When this equation is divided by a common divisor of 44 and 458, an integer is obtained on the left, and so must also be obtained on the right. This, by definition, means that the number is also a divisor of 18. By the same reasoning, any common divisor of 18 and 44 is also a divisor of 458. Since all of the common divisors of 458 and 44 are equal to common divisors of 44 and 18, then in particular the greatest common divisors are equal. So we have gcd(458,44)=gcd(44,18)
The next step in the algorithm is to divide 44 by 18 and find the remainder.
- 44 = 18 × k + r
- 44 = 18 × 2 + 8
Repeat this process; keep dividing the previous divisor by the previous remainder:
- 18 = 8 × 2 + 2
- 8 = 2 × 4 + 0
Our gcd is the last remainder before the zero, in this case, 2. This is because the reasoning that proved gcd(458,44)=gcd(44,18) applies at every step, so gcd(458,44)=gcd(44,18)=gcd(18,8)=gcd(8,2)=gcd(2,0)=2.
The Matrix Method
editWe can construct a matrix that provides an alternative method for calculating the greatest common divisor. In its general form, the matrix is
Recall that one way to write the gcd of two numbers is as an integral linear combination. If we are finding the gcd, for example, we could represent it as as + bt, where a and b are the two numbers we are comparing, and s and t are integers. We also know that b = aq + r where r is the remainder upon division of b by a. After we subtract row 2 from row 1, we get
If r_2 is nonzero, we must continue the process; this time, subtracting row 1 from row 2. We continue this process until one of the r's has been reduced as far as possible. We now have our gcd. The numbers that are in that row, where the 1 and the 0 used to be, represent t and s, respectively.
Let us now look at a computational example.
We see that it would be trivial at this point to go any further; we would just end up with row-2 containing a zero where a used to be. So we look at row-1 and remember that the 1 represents our remainder, 1(=t) multiplies b and -14(=s) multiplies a such that
This can be checked by the Euclidean algorithm that gcd(7,99)=1.
The extended Euclidean algorithm
editWhat happens if we try and reverse the process of the Euclidean algorithm by substituting back? Back-substitution is rather tedious and prone to error, so here is a faster method.
Draw up a table with four columns, label these from left to right q, r, u, v. For convenience label a column i representing the step we're currently up to. Place a and b with the greater of these on top in the column r, and place 1s and 0s accordingly:
Now iterate downwards by taking the quotient of b/a and putting it in the next space in the q column, then of b-aq in the r column.
To update u and v, take
- ui = ui-2-ui-1qi
- vi = vi-2-vi-1qi
Indeed, you are looking for u and v such that au + bv = gcd (a,b). At some point, gcd (a,b) is in fact the remainder at the ith stage, so you might as well compute ui and vi such that aui + bvi = ri, at EACH stage.
Deriving the recurrences found above results from these three equations (the second equation is Euclid's algorithm's basic property, the other two are constraints we set to attain our desired goal):
- aui-1 + bvi-1 = ri-1
- ri-2 = qiri-1 + ri
- aui + bvi = ri
The trick is to then appropriately express ri-2.
Stop writing when you obtain a 0 in the r column.
Finding then, gcd(450,44) (this is the same as gcd(44,450) )
The bold number is the gcd. Observe (9)×450+(-92)×44=2 Clearly these u and v are very special. What can we say about the general case?
Bezout's identity
editIn the above case we have 9×450+(-92)×44=gcd(450,44). So the greatest common divisor of 450 and 44 can be written as a linear combination of 450 and 44 with integer coefficients. This turns out to be true of any pair of integers. This result is known as "Bezout's Identity" and can be stated as follows:
- For any pair of nonzero integers, a and b, there exists integers u and v such that
- au+bv=gcd(a,b)
Proof
- If a and b are any pair of integers, not both 0, then clearly there exist integers u and v such that au+bv is positive (just match the signs of u and v to those of a and b, respectively, for instance), and for all integer u and v, au+bv is also an integer (because the integers are closed under addition and multiplication). So there is a non-empty set of positive integers consisting of numbers of the form au+bv; call it S. Since S is a non-empty set of positive integers, it must have a smallest element (this is the so called Well-ordering principle). Call this number d. The claim is that . Since d belongs to S, then
- (1)
- for suitable u and v. Let n be any positive common divisor of a and b. Since n divides the right side of (1), it also divides d. So for some integer . So any common divisor of a and b is less than or equal to d. Therefore, if d is a common divisor of a and b, it is the greatest one. It only remains to show that d is in fact a common divisor.
- To prove this, it will be shown that any element of S is divisible by d. This will prove that d is a common divisor of a and b because a and b are both elements of S (because a = 1×a + 0×b and b = 0×a + 1×b). Let t be any element of S. Then, by the division algorithm
- for some . If r is not 0, then it is in S. This is because d and t are in S, so
- But, since and d is the least element of S, this is impossible. The only other possibility is that r=0. Therefore any element, t, of S is divisible by d. Since this includes both a and b, d is a common divisor. Combining this with the previous result establishes Bezout's Identity.
The numbers u and v can either be obtained using the tabular methods or back-substitution in the Euclidean Algorithm.
Proof of the Fundamental Theorem of Arithmetic
editOne use of Bezout's identity is in a proof of the Fundamental Theorem of Arithmetic. Before this is proven, two other results are needed: Lemma 1: If a prime number, p, divides a product of two integers, , then it must divide a or b (or both).
- Proof: If p divides both a and b, there is nothing to prove. Assume p does not divide a. If it can be proven under that assumption that p does divide b, the lemma will be proven.
- Since p does not divide a, then gcd(a,p)=1 (because the only divisors of p are 1 and p, but p is not a common divisor). Therefore, by Bezout's Identity, there exist integers u and v such that
- Multiply this equation by b to obtain:
- p divides both terms on the right hand side and, therefore, divides the left hand side. Hence, p divides b, as was to be shown.
Lemma 2: If a prime number, p, divides a product of integers, , then it must divide at least one of the factors.
- Proof: The proof is by induction on n, the number of factors. The statement is true for n=2, by Lemma 1. Assume the statement is true for n=k and consider a product of k+1 factors. If p divides more than one of the factors, once again there is nothing to prove. Assume that p does not divide any of the factors . It will be shown that p must divide . Since the statement is true for n=k, then since p does not divide any of the factors in , it must not divide the product (by Contrapositive). Let . Then . The conclusion then follows by Lemma 1.
Fundamental Theorem of Arithmetic: Any positive integer, n, can be expressed as a product of primes. This product is unique up to the order in which the terms appear.
- Proof: The proof of the first part of the theorem is by induction on n. If n=1, it is the product of 0 primes. Assume all positive integers less than n can be expressed as a product of primes. If n is prime, then it is the product of 1 prime. Assume n is not prime or 1. Then ,for some positive integers a and b both less than n. Since a and b are both less than n, they can be written as a product of primes by the induciton hypothesis. Combining these products gives n as a product of primes as required.
- Now to prove the second part. Assume there are two prime factorizations of n,
- divides the left side and so must also divide the right side. By Lemma 2, this means that must divide one of the . But these are all prime, so the only way can divide is if for some i. Canceling from both sides of the equation forms another equation of the same form. So it can likewise be proven that for some other i, and so on until all the factors on the left are exhausted. After this, there must not be any factors remaining on the right side since it must equal 1. This proves that any two prime factorizations consist of the same prime factors, as was to be shown.
Partitioning the Divisors of Products
editThe Fundamental Theorem of Arithmetic can also be derived from the following lemma:
Lemma: Given integers , , and , if divides (denoted by ), then there exist integers and such that and and .
In other words, an integer that divides a product can itself be factored into a product where each factor divides the corresponding factor from . This means that no new primes are "created" when and are multiplied together.
This Lemma follows from the Fundamental Theorem of Arithmetic and Bezout's identity, but here a more direct proof will be given.
Proof: If any of , , or is , then the Lemma is trivial. In addition, if any of , , or is negative, then if the Lemma holds for the absolute values , , and , then it is trivial to show that the Lemma holds for , , and . It will now be assumed that , , and are all strictly positive integers.
Form an array of integers that has columns and rows. will denote the integer at column and row . Fill the array by sweeping the array row by row starting with row 1, with each row swept starting from column 1. During this "raster" sweep of , assign values to using the following cyclical pattern: . In essence, is the unique integer from the range such that . Since , it is the case that and .
As previously indicated, the "raster sweep" through array is a cyclical progression through the entries of where column index cycles around , and every time transitions from to , row index advances by one step around the cycle .
In the image below, the grid where ; ; and is depicted both explicitly and using a brickwork pattern.
Array can be endlessly replicated and used to form the infinite array . For arbitrary integers and , the block of entries in formed by columns to and rows to is a copy of . For arbitrary integers and , the entry of is the unique integer from the range such that .
Given any column and row , the entry of located at is the unique integer from such that . Given an arbitrary displacement column displacement and row displacement , the difference is separated from by a multiple of . This gives the entries of the following symmetries:
- Given column displacement and columns , and row displacement and rows , then . Specifically if then since the difference between any two entries of is confined to the set .
- Given columns , and rows , if , then shifting by columns and rows does not change the entries of .
The columns of that contain are spaced evenly due to the aforementioned symmetry. Let denote the smallest positive integer such that every column contains .
- The entries and so it must be the case that is an integer multiple of the period : .
- The entries and so it must be the case that is an integer multiple of the period : .
The rows of eventually repeat (not allowing any column shifts) with a period of . A row does not appear twice in a single cycle due to the symmetry of . Row is identical to row so it must be the case that is an integer multiple of the period : .

It will now be proven that by showing that a sub-block of that consists of columns and rows contains every integer from exactly once.
To clarify notation, given the column indices where , and the row indices where , then will denote the sub-block of consisting of columns through to , and rows through to .
Since a row can be uniquely determined from a single cell and the rows only repeat with a period of , any block will contain exactly unique entries.
Columns that contain occur with a period of . Due to the symmetry of , given any integer , columns that contain occur with a period of . Any block will contain exactly unique entries.
Given any integer , integer will occur in every column, and within that column, in every cell. Any block will contain . Any block will contain every integer from exactly once. So therefore . .
Solving linear modular equations - back to Bezout
editBezout's identity above provides us with the key to solving equations in the form
- ax ≡ b (mod m)
Coprime case - gcd(a, m) is 1
editConsider the case where
- ax ≡ b (mod m)
but with gcd(a, m)=1
Because of Bezout's identity
- 1 = au+mv
When we calculate u, this number is special.
Say if we have the equation
- 4x=11 (mod 21)
4 and 21 are coprime since gcd(4,21)=1. Now 1=4*16+(-3)*(21). Our u in this case is 16. Observe now that 4*16=64. 64 (mod 21) = 1. This number u is very special - it is known as the multiplicative inverse. It is the number u on multiplication by a gives 1 mod m. Bezout's identity on calculating gcd(a, m) will always give you the multiplicative inverse of a modulo m. The multiplicative inverse of a is often written a-1 but note that this does not mean 1/a since we have seen in the first sections that we can not always divide in the integers.
Note that in Zp there is one number without a multiplicative inverse - 0. It may be useful to exclude 0 when considering modular arithmetic, so instead of having to say Zp\{0} all the time, we merely write Zp*.
Now since we have the magic multiplicative inverse, our problem becomes relatively easy to solve. 4-1=16 in Z21 and now, on multiplying throughout by 16
- x = 11 × 16 (mod 21)
(since 4×16=1 because 16 is 4's multiplicative inverse mod 21). 11×16=176 and using a calculator or using the division theorem we obtain
- x = 8 (mod 21)
which is our solution! Verify - 8×4 = 32 = 11 (mod 21).
The general case
editConsider the general case where
- ax ≡ b (mod m)
with no restrictions on a, b and m.
Firstly we calculate gcd(a, m) again to obtain d. Now d is a divisor since the d in gcd means greatest common divisor. So we can now divide a and m - but what about b? Since we have calculated the gcd of a and m but not b we have no guarantees that d will divide b. This then becomes a condition that the equation has no solution.
Now we have reduced the problem to the previous coprime case because gcd(a/d, m/d)=1 with d as above. However we do not have 1 solution any more - this is true because we have reduced the solution to being x = c (mod m/d) and we must bring the solution back mod m. This will be come clearer in the examples.
Let's work through some examples.
Example 1. Solve 4x ≡ 3 (mod 20). Firstly, gcd(4, 20) = 4. 4 does not divide 3 and we have no solution.
Example 2. Solve 9x ≡ 6 (mod 15). gcd(9, 15) = 3 and 3 does divide 6 and we have 3 solutions.
Now, divide through by 3 to obtain
- 3x ≡ 2 (mod 5)
gcd(3, 5) = 1 = 3 × 2 + -1 × 5 So the inverse of 3 mod 5 is 2. Now we obtain the solution
- x ≡ 4 (mod 5)
Now in Z15 we must obtain the two extra solutions 9 and 14 mod 15 - 9 mod 5 = 4 and 14 mod 5 = 4.
Generally we can say that if we have the solution to the reduced equation x, the general solution is x+(m/d)k for k={0, 1, .., d-1}.
Chinese Remainder Theorem
editVery often congruence relations are required to hold simultaneously. Given positive integer bases and and arbitrary integers and where and , a common question is what integers satisfy the following congruence relations simultaneously:
The Chinese Remainder Theorem dictates that when , for any choice of and there exists a unique integer such that:
- the only integers that satisfy simultaneously are those that satisfy
In essence, when and are coprime, there is a 1-to-1 correspondence between ordered pairs from and the set .
Proof 1
editProof: To begin, observe that and so it is possible to pair each with a unique ordered pair and vice-versa.
Given any , integer can be reduced modulo to get an integer , and can be reduced modulo to get an integer . Integers and satisfy:
It is not obvious that for any choice of that there exists a unique such that
Let denote an infinite array with two rows indexed by , and an infinite number of columns indexed by . will denote the entry of at column and row . is the unique integer from where .

Given column indices where , then will respectively denote the sub-blocks formed by columns through to and row sets .
Partition into the series of blocks where block is .
Row 1 of block will always be the sequence . Row 2 of block can be uniquely determined by its first entry, since . The blocks only differ by row 2, and row 2 for each block is uniquely determined by its first entry .
and so . This implies that the first entry of row 2 for the next block can be uniquely determined from the first entry of row 2 for the current block.
Since each block is uniquely determined from the previous block, the row 2 pattern for each block will repeat after a regular period of blocks: . Let set denote the total range of values attained by . It is the case that . Let be the minimum positive difference between any two elements from . The cyclical nature of the elements from makes it easy to show that any element is congruent to a multiple of modulo . In essence: . Since is the minimum positive difference between any two elements of , both and are multiples of (in fact, ). Since , it must be the case that . This implies that and that . A total of blocks are encountered before any repetition occurs in array , and therefore all possible columns occur exactly once in a column period of in array . This establishes the Chinese Remainder Theorem.
Proof 2
editA second (more intuitive) proof can be derived by constructing a mesh to depict the space . This mesh is a rectangular array of points with columns and rows. The columns are indexed from left to right by , and the rows are indexed from bottom to top by . Most importantly, the mesh will "wrap around" in the horizontal and vertical dimensions. This means that moving to the right from column will return you to column ; moving to the left from column will send you to column ; moving up from row will return you to row ; and moving down from row will send you to row .
The mesh has points, and the horizontal and vertical coordinates of each point are the remainders from dividing an integer by and respectively. For convenience, given an arbitrary dividend , and will denote the remainders after is divided by and respectively. If the dividend is incremented by , then the coordinate formed by the remainders moves to the right by one step, and up by one step, wrapping around if necessary. corresponds to the coordinate . Increasing in steps of will trace a ray that originates from and moves one step to the right and one step up each interation, wrapping around if necessary. The images below give examples of this ray for and for . In the images below, a copy of column 0 and row 0 appears at the right and top of the mesh respectively to illustrate the wrap around property. When , and are not coprime and fail to satisfy the conditions of the Chinese remainder theorem.
The ray forms diagonal "stripes" in the mesh, and if these stripes are all equally spaced by , then the ray passes through every point in the mesh exactly once proving that every remainder pair is possible and hence the Chinese remainder theorem. When , and are not coprime and fail to satisfy the conditions of the Chinese remainder theorem, hence the ray does not hit every mesh point. The wrap around property of the mesh makes the mesh "symmetric" in both the horizontal and vertical dimensions, which means that if the wrap around "seams" were moved to any column and row where the ray passes through the lower left corner, then the ray is completely unchanged. This requires that the stripes be equally spaced. Let denote this equal spacing, and it will be shown that and . The ray passes through row every steps to the right. The ray passes through , and the wrap around property implies that moving steps to the right returns to this same intersection point. This can only occur if . By a similar argument . If and are coprime, then , the stripes are evenly spaced by , every remainder pair is possible, and the Chinese remainder theorem is therefore true.
Logic
editIntroduction
editIn conventional algebra, letters and symbols are used to represent numbers and the operations associated with them: +, -, ×, ÷, etc. Doing so can help simplify and solve complex problems. In Logic, we seek to express statements, and the connections between them in algebraic symbols - again with the object of simplifying complicated ideas. Unfortunately, like ordinary algebra, the opposite seems true initially. This is probably because simple examples always seem easier to solve by common-sense methods!
Propositions
editA proposition is a statement which has truth value: it is either true (T) or false (F).
Example 1
Which of the following are propositions?
- (a) 17 + 25 = 42
- (b) July 4 occurs in the winter in the Northern Hemisphere.
- (c) The population of the United States is less than 250 million.
- (d) Is the moon round?
- (e) 7 is greater than 12.
- (f) x is greater than y.
Answers
- (a) is a proposition; and of course it has the 'truth value' true.
- (b) is a proposition. Of course, it's false, but it's still a proposition.
- (c) is a proposition, but we may not actually know whether it's true or false. Nevertheless, the fact is that the statement itself is a proposition, because it is definitely either true or false.
- (d) is not a proposition. It's a question.
- (e) is a proposition. It's false again, of course 7<12.
- (f) is a bit more debatable! It's certainly a potential proposition, but until we know the values of x and y, we can't actually say whether it is true or false. Note that this isn't quite the same as (c), where we may not know the truth value because we aren't well-enough informed. See the next paragraph.
Propositional Functions
editA function is, loosely defined, an operation that takes as input one or more parameter values, and produces a single, well-defined output.
You're probably familiar with the sine and cosine functions in trigonometry, for example. These are examples of functions that take a single number (the size of an angle) as an input and produce a decimal number (which in fact will lie between +1 and -1) as output.
If we want to, we can define a function of our own, say RectangleArea, which could take two numbers (the length and width of a rectangle) as input, and produce a single number as output (formed by multiplying the two input numbers together).
In (f) above, we have an example of a Propositional Function. This is a function that produces as output not a number like sine, cosine or RectangleArea, but a truth value. It's a statement, then, that becomes a proposition when it is supplied with one or more parameter values. In (f), the parameters are x and y. So if x = 2 and y = 7, its output is False; if x = 4 and y = -10, its output is True.
More about propositional functions later.
Notation
editWe shall often represent propositions by lower-case letters p, q, ...
Compound Propositions
editPropositions may be modified by means of one or more logical operators to form what are called compound propositions.
There are three logical operators:
- conjunction: meaning AND
- disjunction: ∨ meaning OR
- negation: ¬ meaning NOT
Example 2
- p represents the proposition "Henry VIII had six wives".
- q represents the proposition "The English Civil War took place in the nineteenth century".
- (a) Connect these two propositions with OR. Is the resulting compound proposition true or false?
- (b) Now connect them with AND. Is this compound proposition true or false?
- (c) Is the 'opposite' of p true or false?
Answers
- (a) p ∨ q is "Henry VIII had six wives or the English Civil War took place in the nineteenth century"
- This is true. The first part of the compound proposition is true, and this is sufficient to make the whole statement true – if a little odd-sounding!
If you think that this example seems very artificial, imagine that you're taking part in a History Quiz; there are two questions left, and you need to get at least one right to win the quiz. You make the two statements above about Henry VIII and the Civil War. Do you win the quiz? Yes, because it is true that either Henry VIII had six wives or the English Civil War took place in the nineteenth century.
Note that this is an inclusive OR: in other words, we don't rule out both parts being true. So p ∨ q means "Either p is true, or q is true, or both".
- (b) p q is "Henry VIII had six wives and the English Civil War took place in the nineteenth century"
- This is false.
To be true, both parts would have to be true. This is equivalent to your needing both questions right to win the quiz. You fail, because you got the second one wrong.
- (c) The opposite of p, which we write as ¬p, is "Henry VIII did not have six wives". This is clearly false. And in general, if p is true, then ¬p is false, and vice versa.
Example 3
- p is "The printer is off-line"
- q is "The printer is out of paper"
- "r" is "The document has finished printing"
- Write as English sentences, in as natural a way as you can:
- (a) p ∨ q
- (b) r q
- (c) q ¬r
- (d) ¬(p ∨ q)
Answers
- (a) The printer is off-line or out of paper.
Notice how we often leave words out when we're writing or speaking English. This sounds much more natural than "The printer is off-line or the printer is out of paper".
- (b) The document has finished printing and the printer is out of paper.
The subject of each part of the sentence is different now, so no words are missing this time.
- (c) The printer is out of paper and the document has not finished printing.
But and And
The statement in (c) could be someone reporting a problem, and they might equally well say:
- (c) The printer is out of paper but the document has not finished printing.
So note that, in logic, but and and mean the same thing. It's just that we use but to introduce a note of contrast or surprise. For example, we might well say:
- The sun is shining brightly, but it's freezing cold outside.
Logically, we could use and to connect both parts of this sentence, but(!) it's more natural to use but.
In (d) what does ¬(p ∨ q) mean? Well, p ∨ q means either p is true or q is true (or both). When we place ¬ in front, we negate this. So it means (literally):
- It is not true that either the printer is off-line or the printer is out of paper.
In other words:
- (d) The printer is neither off-line nor out of paper.
Notice that it's often convenient to translate ¬ using the phrase 'It is not true that …'.
Logic Exercise 1
editClick link for Logic Exercise 1.
Truth Tables
editConsider the possible values of the compound proposition p q for various combinations of values of p and q. The only combination of values that makes p q true is where p and q are both true; any other combination will include a false and this will render the whole compound proposition false. On the other hand, the compound proposition p ∨ q will be true if either p or q (or both) is true; the only time p ∨ q is false is when both p and q are false.
We summarise conclusions like these in what is called a Truth Table, the truth table for AND being:
| p | q | p q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
The truth table for OR is:
| p | q | p ∨ q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
The order of the Rows in a Truth Table
editNotice the pattern of T's and F's in the first two columns of each of the truth tables above. In the first column (the truth values of p), there are 2 T's followed by 2 F's; in the second (the values of q), the T's and F's change on each row. We shall adopt this order of the rows throughout this text. Adopting a convention for the order of the rows in a Truth Table has two advantages:
- It ensures that all combinations of T and F are included. (That may be easy enough with just two propositions and only four rows in the Truth Table; it's not so easy with, say, 4 propositions where there will be 16 rows in the table.)
- It produces a standard, recognisable output pattern of T's and F's. So, for example, T, F, F, F is the output pattern (or 'footprint' if you like) of AND (), and T, T, T, F is the footprint of OR (∨).
The truth table for NOT
editEach of the two truth tables above had two 'input' columns (one for the values of p and one for q), and one 'output' column. They each needed four rows, of course, because there are four possible combinations of T's and F's when two propositions are combined. The truth table for NOT (¬) will be simpler, since ¬ is a unary operation – one that requires a single proposition as input. So it just two columns – an input and an output – and two rows.
| p | ¬p |
| T | F |
| F | T |
Drawing up Truth Tables
editThe method for drawing up a truth table for any compound expression is described below, and four examples then follow. It is important to adopt a rigorous approach and to keep your work neat: there are plenty of opportunities for mistakes to creep in, but with care this is a very straightforward process, no matter how complicated the expression is. So:
- Step 1: Rows
- Decide how many rows the table will require. One input requires only two rows; two inputs require 4 rows; three require 8, and so on. If there are n propositions in the expression, 2n rows will be needed.
- Step 2: Blank Table
- Draw up a blank table, with the appropriate number of input columns and rows, and a single output column wide enough to accommodate comfortably the output expression. If 8 or more rows are needed, you'll probably find it helps to rule a horizontal line across the table every four rows, in order to keep your rows straight.
- Step 3: Input Values
- Fill in all the input values, using the convention above for the Order of Rows in a Truth Table; that is to say, begin with the right-most input column and fill in the values T and F, alternating on every row. Then move to the next column to the left, and fill in T's and F's changing on every second row. And so on for all the remaining columns. The left-most column will then contain T's in the first half of all the rows in the table, and F's in the second half.
- Step 4: Plan your strategy
- Study carefully the order in which the operations involved in evaluating the expression are carried out, taking note of any brackets there may be. As in conventional algebra, you don't necessarily work from left to right. For example, the expression p ∨ ¬q will involve working out ¬q first, then combining the result with p using ∨. When you've worked out the order in which you need to carry out each of the operations, rule additional columns under the output expression - one for each stage in the evaluation process. Then number each of the columns (at its foot) in the order in which it will be evaluated. The column representing the final output will be the last stage in the evaluation process, and will therefore have the highest number at its foot.
- Step 5: Work down the columns
- The final stage is to work down each column in the order that you've written down in Step 4. To do this, you'll use the truth tables for AND, OR and NOT above using values from the input columns and any other columns that have already been completed. Remember: work down the columns, not across the rows. That way, you'll only need to think about one operation at a time.
You're probably thinking that this all sounds incredibly complicated, but a few examples should make the method clear.
Worked examples
editExample 4
Produce truth tables for:
- (a) ¬(¬p)
- (b) p (¬q)
- (c) (p q) ∨ (¬p ∨ ¬q)
- (d) q (p ∨ r)
Solutions
(a) ¬(¬p) is pretty obviously the same as p itself, but we'll still use the above method in this simple case, to show how it works, before moving on to more complicated examples. So:
- Step 1: Rows
There's just one input variable here, so we shall need two rows.
- Step 2: Blank Table
So the table is:
| p | ¬(¬p) |
| . | |
| . |
- Step 3: Input Values
Next, we fill in the input values: just one T and one F in this case:
| p | ¬(¬p) |
| T | |
| F |
- Step 4: Plan your strategy
As in 'ordinary' algebra we evaluate whatever's in brackets first, so we shall first (1) complete the (¬p) values, followed (2) by the left-hand ¬ symbol, which gives us the final output values of the whole expression. We rule an extra column to separate these two processes, and write the (1) and (2) at the foot of these two columns. Thus:
| p | ¬ | (¬p) |
| T | ||
| F | ||
| (2)
Output |
(1) |
- Step 5: Work down the columns
Finally we insert the values in column (1) – F followed by T – and then use these values to insert the values in column (2). So the completed truth table is:
| p | ¬ | (¬p) |
| T | T | F |
| F | F | T |
| (2)
Output |
(1) |
As we said at the beginning of this example, ¬(¬p) is clearly the same as p, so the pattern of the output values, T followed by F, is identical to the pattern of the input values. Although this may seem trivial, the same technique works in much more complex examples, where the results are far from obvious!
(b) p (¬q)
- Step 1
There are two input variables, p and q, so we shall need four rows in the table.
- Steps 2 & 3
In the q column write T's and F's alternating on every row; in the p column alternate every two rows. At this stage, the table looks like this:
| p | q | p (¬q) |
| T | T | |
| T | F | |
| F | T | |
| F | F |
- Steps 4 & 5
As Example (a), we begin (1) by evaluating the expression in brackets, (¬q), and then (2) we combine these results with p using the operator. So we divide the output section of the table into two columns; then work down column (1) and finally column (2). The completed table is:
| p | q | p | (¬q) |
| T | T | F | F |
| T | F | T | T |
| F | T | F | F |
| F | F | F | T |
| (2)
output |
(1) |
(c) (p q) ∨ (¬p ∨ ¬q)
- Steps 1 to 3
As in Example (b).
- Steps 4 & 5
There will be 5 stages in evaluating the expression (p q) ∨ (¬p ∨ ¬q). In order, they are:
- (1) The first bracket: (p q)
- (2) The ¬p in the second bracket
- (3) The ¬q in the second bracket
- (4) The ∨ in the second bracket
- (5) The ∨ between the two brackets. This final stage, then, represents the output of the complete expression.
Reminder: Don't work across the rows; work down the columns in order (1) to (5). That way, you'll only have to deal with a single operation at a time.
The completed table is:
| p | q | (p q) | ∨ | (¬p | ∨ | ¬q) |
| T | T | T | T | F | F | F |
| T | F | F | T | F | T | T |
| F | T | F | T | T | T | F |
| F | F | F | T | T | T | T |
| (1) | (5)
output |
(2) | (4) | (3) |
Notice that the output consist solely of T's. This means that (p q) ∨ (¬p ∨ ¬q) is always true whatever the values of p and q. It is therefore a tautology (see below).
(d) q (p ∨ r)
This simple expression involves 3 input variables, and therefore requires 23 = 8 rows in its truth table. When drawing this truth table by hand, rule a line below row 4 as an aid to keeping your working neat. It is shown as a double line in this table. The completed table is shown below.
| p | q | r | q | (p ∨ r) |
| T | T | T | T | T |
| T | T | F | T | T |
| T | F | T | F | T |
| T | F | F | F | T |
| F | T | T | T | T |
| F | T | F | F | F |
| F | F | T | F | T |
| F | F | F | F | F |
| (2)
output |
(1) |
Tautology
editAn expression which always has the value true is called a tautology.
In addition, any statement which is redundant, or idempotent, is also referred to as a tautology, and for the same reason previously mentioned. If P is True then we can be sure that P ∨ P is true, and P ∧ P is also true.
Logic Exercise 2
editClick link for Logic Exercise 2.
Order of Precedence
editIn 'ordinary' algebra, the order of precedence in carrying out operations is:
- 1 brackets
- 2 exponents (powers)
- 3 × and ÷
- 4 + and -
In the algebra of logic, brackets will often be inserted to make clear the order in which operations are to be carried out. To avoid possible ambiguity, the agreed rules of precedence are:
- 1 brackets
- 2 NOT (¬)
- 3 AND ()
- 4 OR (∨)
So, for example, p ∨ q r means:
- Evaluate q r first.
- Then combine the result with p ∨.
Since it would be easy to misinterpret this, it is recommended that brackets are included, even if they are not strictly necessary. So p ∨ q r will often be written p ∨ (q r).
Logically Equivalent Propositions
editLook back to your answers to questions 2 and 3 in Exercise 2. In each question, you should have found that the last columns of the truth tables for each pair of propositions were the same.
Whenever the final columns of the truth tables for two propositions p and q are the same, we say that p and q are logically equivalent, and we write:
- p ≡ q
Example 5
Construct truth tables for
- (i) p ∨ (q r), and
- (ii) (p ∨ q) (p ∨ r),
and hence show that these propositions are logically equivalent.
Solution
(i)
| p | q | r | p ∨ | (q r) |
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | T | F |
| T | F | F | T | F |
| F | T | T | T | T |
| F | T | F | F | F |
| F | F | T | F | F |
| F | F | F | F | F |
| (2)
output |
(1) |
(ii)
| p | q | r | (p ∨ q) | (p ∨ r) | |
| T | T | T | T | T | T |
| T | T | F | T | T | T |
| T | F | T | T | T | T |
| T | F | F | T | T | T |
| F | T | T | T | T | T |
| F | T | F | T | F | F |
| F | F | T | F | F | T |
| F | F | F | F | F | F |
| (1) | (3)
output |
(2) |
The outputs in each case are T, T, T, T, T, F, F, F. The propositions are therefore logically equivalent.
Example 6
Construct the truth table for ¬(¬p ∨ ¬q), and hence find a simpler logically equivalent proposition.
Solution
| p | q | ¬ | (¬p | ∨ | ¬q) |
| T | T | T | F | F | F |
| T | F | F | F | T | T |
| F | T | F | T | T | F |
| F | F | F | T | T | T |
| (4)
output |
(1) | (3) | (2) |
We recognise the output: T, F, F, F as the 'footprint' of the AND operation. So we can simplify ¬(¬p ∨ ¬q) to
- p q
Laws of Logic
editLike sets, logical propositions form what is called a Boolean Algebra: the laws that apply to sets have corresponding laws that apply to propositions also. Namely:
Commutative Laws
- p q ≡ q p
- p ∨ q ≡ q ∨ p
Associative Laws
- (p q) r ≡ p (q r)
- (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
Distributive Laws
- p (q ∨ r) ≡ (p q) ∨ (p r)
- p ∨ (q r) ≡ (p ∨ q) ( p ∨ r)
Idempotent Laws
- p p ≡ p
- p ∨ p ≡ p
Identity Laws
- p T ≡ p
- p ∨ F ≡ p
Domination laws
- p ∨ T ≡ T
- p F ≡ F
Involution Law
- ¬(¬p) ≡ p
De Morgan’s Laws
- ¬(p ∨ q) ≡ (¬p) (¬q)
- (sometimes written p NOR q)
- ¬(p q) ≡ (¬p) ∨ (¬q)
- (sometimes written p NAND q)
Complement Laws
- p ¬p ≡ F
- p ∨ ¬p ≡ T
- ¬T ≡ F
- ¬F ≡ T
Worked Examples
editExample 7
Propositional functions p, q and r are defined as follows:
- p is "n = 7"
- q is "a > 5"
- r is "x = 0"
Write the following expressions in terms of p, q and r, and show that each pair of expressions is logically equivalent. State carefully which of the above laws are used at each stage.
(a)
- ((n = 7) ∨ (a > 5)) (x = 0)
- ((n = 7) (x = 0)) ∨ ((a > 5) (x = 0))
(b)
- ¬((n = 7) (a ≤ 5))
- (n ≠ 7) ∨ (a > 5)
(c)
- (n = 7) ∨ (¬((a ≤ 5) (x = 0)))
- ((n = 7) ∨ (a > 5)) ∨ (x ≠ 0)
Solutions
(a)
- (p ∨ q) r
- (p r) ∨ (q r)
| (p ∨ q) r | = r (p ∨ q) | Commutative Law |
| = (r p) ∨ r q) | Distributive Law | |
| = (p r) ∨ (q r) | Commutative Law (twice) |
(b)
First, we note that
- ¬q is "a ≤ 5"; and
- ¬p is "n ≠ 7".
So the expressions are:
- ¬(p ¬q)
- ¬p ∨ q
| ¬(p ¬q) | = ¬p ∨ ¬(¬q) | De Morgan's Law |
| = ¬p ∨ q | Involution Law |
(c)
First, we note that
- ¬r is "x ≠ 0".
So the expressions are:
- p ∨ (¬(¬q r))
- (p ∨ q) ∨ ¬r
| p ∨ (¬(¬q r)) | = p ∨ (¬(¬q) ∨ ¬r) | De Morgan's Law |
| = p ∨ (q ∨ ¬r) | Involution Law | |
| = (p ∨ q) ∨ ¬r | Associative Law |
Logic Exercise 3
editClick link for Logic Exercise 3.
Logic Page 2
editConditional Propositions
editExample 8
Discuss what Andy means when he says to Bernard: "If you want some more coffee, there’s some in the pot".
What Andy probably means is simply "There's some coffee in the pot, and if you want some, help yourself". Almost certainly, he doesn't really mean to imply that the presence (or otherwise) of the coffee in the pot is somehow dependent upon Bernard's desire for some.
As you may have realised, we are sometimes very sloppy in our use of English! One of the things we need to do if we want to represent a sentence using logic symbols, is to work out what it really means.
The ⇒ IMPLICATION
editExample 9
Suppose that
- p is "The weather is warm"; and
- q is "I go swimming at lunchtime"
Then we can represent the conditional proposition "If the weather is warm, then I go swimming at lunchtime" by the symbols:
- p ⇒ q
So ⇒ means: "if ... then", or "implies (or means) that".
Other ways of saying the same thing are:
- "The weather is warm means that I go swimming at lunchtime"
- "Whenever the weather is warm, I go swimming at lunchtime"
- "The weather is warm only if I go swimming at lunchtime"
Be careful with the last statement. It does not follow (and does not correspond to) the logic of our expression p ⇒ q. It changes the direction of ⇒ , as it were. Using word "if" at this place in the sentence changes causality of the proposition, such as my doing swimming at lunchtime means the weather is warm. This would be q ⇒ p, a reversal of conditions in our original expression. Words "only if" mean that if on a particular day I didn't go swimming at lunchtime, then the weather could not have been warm on that day, also a reverse implication. Our expression does not, of course, mean that my going swimming (or otherwise) determines the weather on that day, it’s another way around!
Necessary and Sufficient Conditions
editSuppose that last Tuesday I went swimming at lunchtime. Given p and q as above, and given also that p ⇒ q, can you be sure that the weather was warm last Tuesday?
The answer is that, no, you can't. I might have gone swimming anyway, for some other reason.
Note, then, that p ⇒ q means that p is a sufficient condition for q. It is not, however, a necessary condition: q can still be true without p.
Other ways of saying this:
"I can go swimming at lunchtime even if the weather is not warm"
"I can go swimming at lunchtime regardless of the weather"
The truth table for ⇒
editNote that p ⇒ q is itself a proposition; i.e. it has a truth value - it may or may not be the case that if the weather is warm, I go swimming at lunchtime.
Now the value of the proposition p ⇒ q depends upon the combination of the values of p and q. So we can construct its truth table:
| p | q | p ⇒ q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Note in particular the (perhaps surprising) third line of this table! The fact is that p ⇒ q means that we cannot draw any conclusions about q if p is false. That is to say, if p is false, q may equally well be true or false without contradicting the truth of p ⇒ q.
To put this another way, p ⇒ q is false only when p is T and q is F; i.e. a true statement cannot imply a false one.
To clarify this further, consider the statement above: "If the weather is warm, then I go swimming at lunchtime". This says nothing about what happens when the weather is not warm: I may go swimming or I may not. The only time this statement is untrue is when the weather is warm, but I don't go swimming.
Biconditional Propositions
editAs we have already noted, we often use English in a very imprecise way. Using Example 9, suppose what I really mean to say is:
- If the weather is warm I go swimming at lunchtime, and if it’s not I don’t.
In this case p and q are either both true or both false: you can’t have one without the other. We could re-phrase this and say:
- I go swimming at lunchtime if and only if the weather is warm.
The phrase "if and only if" is represented by the symbol ⇔, and so we can say in this case:
- p ⇔ q
In such a case as this, p is a necessary and sufficient condition for q.
Example 10
p is "x2 = 9". Find a suitable statement q about x (rather than x2) for which p ⇔ q is true.
Solution
If x = 3, then certainly x2 = 9. So if q is "x = 3", then q ⇒ p is true, and this would make q a sufficient condition.
But is it necessary and sufficient? No, because 3 is not the only number whose square is 9. x = -3 would also make x2 = 9.
- To ensure a necessary and sufficient q, then, we would have to say:
- q is "x = ±3"
Logically Equivalent
editWe have said that p ⇔ q means that p and q are either both true, or both false, and we can therefore say that in such a case they are logically equivalent.
The truth table for ⇔
editSince p ⇔ q means that p and q are either both true or both false, the truth table for ⇔ is:
| p | q | p ⇔ q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Example 11
By drawing up a truth table show that
- p ⇔ q ≡ (p ⇒ q) (q ⇒ p)
Solution
The truth table for (p ⇒ q) (q ⇒ p) is:
| p | q | (p ⇒ q) | (q ⇒ p) | |
| T | T | T | T | T |
| T | F | F | F | T |
| F | T | T | F | F |
| F | F | T | T | T |
| 1 | 3
output |
2 |
The output is T, F, F, T which is the same as the output for p ⇔ q, and therefore
- p ⇔ q ≡ (p ⇒ q) (q ⇒ p)
The ⇐ Notation
editWe sometimes use ⇐ to mean "is implied by". So q ⇐ p is an alternative way of writing p ⇒ q, and we could have written Example 11 as:
- p ⇔ q ≡ (p ⇒ q) (p ⇐ q)
Logic Exercise 4
editClick the link for Logic Exercise 4.
Predicate Logic
editSo far, we have considered only Propositional Logic, with statements like:
- p is "All people with red hair have fiery tempers"
- q is "Joe has red hair"
Given p and q as above and r is "Joe has a fiery temper", we can write:
- p q ⇒ r
If we want to make a statement about Brenda having red hair, and therefore a fiery temper, we should need further propositions, like this:
- s is "Brenda has red hair"
- t is "Brenda has a fiery temper"
and so:
- p s ⇒ t
… and so on.
Each time we want to make a statement about another person having red hair, and therefore a fiery temper (which may or may not be true!), we shall need further propositions. A much better way of representing these ideas is to use predicates like this:
- redHair is the phrase "... has red hair"
(Notice that redHair is not a proposition. Why not?)
We can now use this predicate to form statements about anyone who has red hair; like this:
- redHair(Joe) is "Joe has red hair"
- redHair(Brenda) is"‘Brenda has red hair"
... and so on.
In the same way, we can define the predicate fieryTemper to stand for the phrase:
- "... has a fiery temper"
So the statement "If Joe has red hair, then he has a fiery temper" can be represented by:
- redHair(Joe) ⇒ fieryTemper(Joe)
and the statement "If Brenda has red hair, then she has a fiery temper" by:
- redHair(Brenda) ⇒ fieryTemper(Brenda)
Notation
editWe shall use single words or several words joined together, using upper- and lower-case letters as shown, to denote predicates.
The "object" to which the predicate applies - a person, number, or whatever - will be written in parenthesis following the predicate.
Negation
editWith red Hair defined as above:
- ¬with red Hair is "it is not the case that with red hair"
Logic Exercise 5
editClick the link for Logic Exercise 5.
Propositional Functions
editIf we want to talk about general, undefined, predicates, we shall use upper-case letters: P, Q, ..., and if we want a general, undefined, object, we shall use a lower-case letter: x, y, ...
So if P is "... has property P", then P(x) is "x has property P".
- P(x) can then be described as a propositional function whose predicate is P.
A function has the property that it returns a unique value when we know the value(s) of any parameter(s) supplied to it. P(x) is therefore a function since it returns a truth value which depends upon the value of its parameter, x.
For example, if American(x) is the propositional function "x is an American", then American(x) will return the value
- T if x = Bill Clinton; and the value
- F if x = HM The Queen
Quantifiers
editWe now extend the ideas in Exercise 5 above. Suppose we want to make statements like:
- (a) All of my friends are wealthy.
- (b) Some of my friends are boring.
The problem here is that we are making statements about my friends in general, without referring to a particular individual. So we need to define propositional functions as follows:
- friend(x) is "x is a friend of mine"
- wealthy(x) is "x is wealthy"
- boring(x) is "x is boring"
We can then write the two statements above as:
- (a) For all x, friend(x) ⇒ wealthy(x)
- (b) For some x, friend(x) boring(x)
Notation: ∀ and ∃
editThe symbol ∀ (called the universal quantifier) stands for the phrase "For all …"
So we can write (a) above as:
- (a) ∀ x, friend(x) ⇒ wealthy(x)
The symbol ∃ (called the existential quantifier) stands for the phrase "For some …"
So we can write (b) above as:
- (b) ∃ x, friend(x) boring(x)
Plural or singular?
editNote that, although statements (a) and (b) above use plural words – all, are, some, friends – when we symbolise them, the predicates and the variables are singular: x is wealthy, x is boring, etc. It is important to realise, then, that x can stand for just one value at a time.
So the symbolic statement:
- ∀ x, friend(x) ⇒ wealthy(x)
would be literally translated using singular words as:
- "For each value of x, if x is a friend of mine, then x is wealthy".
and
- ∃ x, friend(x) boring(x)
is more literally translated:
- "For at least one value of x, x is a friend of mine and x is boring".
To emphasise this, you might find it helpful to use the following as translations of the symbols:
- ∀ means "For each (value of) ..."
and
- ∃ means "For at least one (value of) ..."
We can now make our earlier statement that "All people with red hair have fiery tempers" using Propositional Function notation as follows:
- redHair(x) is: "x has red hair"
- fieryTemper(x) is: "x has a fiery temper"
Now "All people with red hair have fiery tempers" is re-written in the singular as:
- For each value of x, if x has red hair, then x has a fiery temper.
In symbols, then:
- ∀ x, redHair(x) ⇒ fieryTemper(x)
Example 12
Define suitable propositional functions and then express in symbols:
- (a) Some cats understand French.
- (b) No footballers can sing.
- (c) At least one lecturer is not boring.
- (d) I go swimming every sunny day.
Solutions
(a) Re-write in the singular: "At least one cat understands French". So we shall need to define propositional functions as:
- cat(x) is "x is a cat"
- French(x) is "x understands French"
So there is at least one x that is a cat and understands French; or, in symbols:
- ∃x, cat(x) French(x)
(b) Re-write in the singular: "It is not true that at least one footballer can sing". So:
- footballer(x) is "x is a footballer"
- sing(x) is "x can sing"
In symbols, then:
- ¬ (∃x, footballer(x) sing(x))
Alternatively, we might re-write "No footballers can sing" as "For each x, if x is a footballer, then x cannot sing". In symbols, then, this gives the equally valid solution:
- ∀ x, footballer(x) ⇒ ¬ sing(x)
(c) This is already in the singular; so:
- lecturer(x) is "x is a lecturer"
- boring(x) is "x is boring"
So:
- ∃ x, lecturer(x) ¬ boring(x)
(d) In this example, it is important to realise what the variable represents. In (a) to (c) the variable x has denoted an animal or a person. In the sentence "I go swimming every sunny day" it is the day that changes, and, with it, the weather and my going swimming. So we must form our propositional functions around a variable x that stands for a day. Thus:
- sunny(x) is "x is a sunny day"
- swimming(x) is "x is a day when I go swimming"
Then, re-writing "I go swimming every sunny day" in the singular, we get:
- "For each day, if it is a sunny day then it is a day when I go swimming"
So, in symbols:
- ∀x, sunny(x) ⇒ swimming(x)
Logic Exercise 6
editClick the link for Logic Exercise 6.
Universe of Discourse
editMany of the propositions in Exercises 5 and 6 referred to 'my friends'. For example, consider the proposition: "All of my friends are either wealthy or clever."
Using predicates, we can symbolise this as:
- ∀ x, friend(x) ⇒ (wealthy(x) ∨ clever(x))
However, if we agreed that the variable x can only stand for one of my friends, then we could symbolise this more simply as:
- ∀ x, wealthy(x) ∨ clever(x)
For a given propositional function P(x), the universe of discourse is the set from which the value of x may be chosen. Defining a universe of discourse can simplify the symbolisation of propositional functions. If a universe of discourse is not defined, then we shall have to assume that any object or individual may be substituted for x.
Example 13
Define, in each case, a suitable universe of discourse and predicates to symbolise:
- (a) Some students are hard-working or drink too much.
- (b) Everybody was hot and someone fainted.
Solutions
(a) Define the following:
- Universe of discourse = {students}
- hardWorking(x) is "x is hard-working"
- drink(x) is "x drinks too much"
Writing in the singular: "For at least one x, x is hard-working or x drinks too much", we get:
- ∃ x, hardWorking(x) ∨ drink(x)
(b) In the given sentence, the word "everybody" clearly doesn't mean everybody in the whole world, simply everybody in the story being recounted. So we can define as follows:
- Universe of discourse = {people in the story}
- hot(x) is "x was hot"
- fainted(x) is "x fainted"
Then, in the singular, we have "For each x, x was hot and for at least one x, x fainted". So:
- ∀ x, hot(x) ∃ x, fainted(x)
Two-place Predicates
editThe predicates we have looked at so far have been one-place predicates. To convert each predicate into a proposition, we have had to supply a single object or individual - the value of a single parameter, if you like.
We can create predicates which require two objects (or parameter values) to be supplied to convert them to propositions. Such predicates are called two-place predicates.
Example 14
Consider the following predicates:
- greaterThan is "… is greater than …"
- loves is "… loves …"
- belongsTo is "… belongs to …"
Then the following are two-variable propositional functions:
- greaterThan(x, y) is "x is greater than y"
- loves(x, y) is "x loves y"
- belongsTo(x, y) is "x belongs to y"
So, for example, the following are propositions:
- greaterThan(5, 2) is "5 is greater than 2"
- loves(Bob, Lizzie) is "Bob loves Lizzie"
- belongsTo(This coat, Harry) is "This coat belongs to Harry"
Two-place Predicates and Quantifiers
editWith the predicates above, we can quantify over one variable:
- ∀ x, belongsTo(x, me) is "Everything belongs to me"
- ∃ x, greaterThan(2, x) is "2 is greater than something"
- ∀ x, loves(Mary, x) is "Mary loves everyone"
... or both variables:
- ∀ x, ∃y, loves(x, y) is "Everybody loves somebody"
- ∃ x, ∀ y, loves(x, y) is "Somebody loves everybody"
- ∃ x, ∃ y, loves(x, y) is "Somebody loves somebody"
- ∀ x, ∀ y, loves(x, y) is "Everybody loves everybody"
Negation of Quantified Propositional Functions
editIn Question 5 of Exercise 1, we had to say which of several options represented the negation of a proposition. Let’s look at this again, using our Quantified Propositional Function notation.
Example 15
Consider the negation of the proposition
- "All sheep are black".
The negation is:
- "It is not true that all sheep are black".
which is equivalent to:
- "At least one sheep is not black".
If we define the universe of discourse as {sheep} and isBlack in the obvious way, then we can symbolise all this as follows:
- ¬ (∀ x, isBlack(x)) ≡ ∃ x, ¬isBlack(x)
Now consider the proposition
- "Some sheep are black".
The negation of this is:
- "It is not true that some sheep are black"
which is equivalent to:
- "All sheep are not black"
This can then be symbolised as:
- ¬ (∃ x, isBlack(x)) ≡ ∀ x, ¬isBlack(x)
We can generalise what we have found here to any propositional function P(x), as follows:
- ¬(∀ x, P(x)) ≡ ∃ x, ¬ P(x)
- ¬(∃ x, P(x)) ≡ ∀ x, ¬P(x)
Logic Exercise 7
editClick the link for Logic Exercise 7.
Enumeration
editDiscrete Mathematics/Enumeration
Graph theory
editIntroduction
editA graph is a mathematical way of representing the concept of a "network".
A network has points, connected by lines. In a graph, we have special names for these. We call these points vertices (sometimes also called nodes), and the lines, edges.
Here is an example graph. The edges are red, the vertices, black.
In the graph, are vertices, and are edges.
Definitions of graph
editThere are several roughly equivalent definitions of a graph. Set theory is frequently used to define graphs. Most commonly, a graph is defined as an ordered pair , where is called the graph's vertex-set and is called the graph's edge-set. Given a graph , we often denote the vertex—set by and the edge—set by . To visualize a graph as described above, we draw dots corresponding to vertices . Then, for all we draw a line between the dots corresponding to vertices if and only if there exists an edge . Note that the placement of the dots is generally unimportant; many different pictures can represent the same graph.
Alternately, using the graph above as a guide, we can define a graph as an ordered triple :
- a set of vertices, commonly called V
- a set of edges, commonly called E
- a relation that maps to each edge a set of endpoints, known as the edge-endpoint relation. We say an edge is incident to a vertex iff .
In the above example,
- V={v1, v2, v3, v4}
- E={e1, e2, e3, e4, e5}
- f such that e1 maps to {v1, v2}, e2 maps to {v1, v3}, e3 maps to {v1, v4}, e4 maps to {v2, v4}, and e5 maps to {v3, v4}.
If is not injective — that is, if such that — then we say that is a multigraph and we call any such edges multiple edges. Further, we call edges such that loops. Graphs without multiple edges or loops are known as simple graphs.
Graphs can, conceivably, be infinite as well, and thus we place no bounds on the sets V and E. We will not look at infinite graphs here.
Directions, Weights, and Flows
editWe define a directed graph as a graph such that maps into the set of ordered pairs rather than into the family of two-element sets . We can think of an edge such that as 'pointing' from to . As such we would say that is the tail of edge and that is the head. This is one of the vagaries of graph theory notation, though. We could just as easily think of as the head and as the tail. To represent a directed graph, we can draw a picture as described and shown above, but place arrows on every edge corresponding to its direction.
In general, a weight on a graph is some function .
A flow is a directed graph paired with a weight function such that the weight "going into" any vertex is the same amount as the weight "going out" of that vertex. To make this more formal, define sets
Then, formally stated, our requirement on the weight function is
Algebraic Graph Theory
editWhile set theory is frequently used when discussing graphs, other approaches can simplify certain operations. A set can be defined using an adjacency matrix where element is a 1, if there is an edge between vertex i and vertex j and 0 otherwise.
Special Graphs
edit
Some graphs occur frequently enough in graph theory that they deserve special mention. One such graphs is the complete graph on n vertices, often denoted by Kn. This graph consists of n vertices, with each vertex connected to every other vertex, and every pair of vertices joined by exactly one edge. Another such graph is the cycle graph on n vertices, for n at least 3. This graph is denoted Cn and defined by V := {1,2,..,n} and E := {{1,2},{2,3}, ..., {n-1,n},{n,1}}. Even easier is the null graph on n vertices, denoted Nn; it has n vertices and no edges! Note that N1 = K1 and C3 = K3.
Some Terms
editTwo vertices are said to be adjacent if there is an edge joining them. The word incident has two meanings:
- An edge e is said to be incident to a vertex v if v is an endpoint of e.
- Two edges are also incident to each other if both are incident to the same vertex.
Two graphs G and H are said to be isomorphic if there is a one-to-one function from (or, if you prefer, one-to-one correspondence between) the vertex set of G to the vertex set of H such that two vertices in G are adjacent if and only if their images in H are adjacent. (Technically, the multiplicity of the edges must also be preserved, but our definition suffices for simple graphs.)
Subgraphs
edit
A subgraph is a concept akin to the subset. A subgraph has a subset of the vertex set V, a subset of the edge set E, and each edge's endpoints in the larger graph has the same edges in the subgraph. A
A subgraph of is generated by the vertices {} if the edge set of consists of all edges in the edge set of that joins the vertices in {}.
A path is a sequence of edges such that ei is adjacent to ei+1 for all i from 1 to N-1. Two vertices are said to be connected if there is a path connecting them.
Trees and Bipartite Graphs
editA tree is a graph that is (i) connected, and (ii) has no cycles. Equivalently, a tree is a connected graph with exactly edges, where there are nodes in the tree.
A Bipartite graph is a graph whose nodes can be partitioned into two disjoint sets U and W such that every edge in the graph is incident to one node in U and one node in W. A tree is a bipartite graph.
A complete bipartite graph is a bipartite graph in which each node in U is connected to every node in W; a complete bipartite graph in which U has vertices and V has vertices is denoted .
Adjacent,Incident,End Vertices
Self loops,Parallel edges,Degree of Vertex
Pendant Vertex : Vertex Degree one "Pendant Vertex" Isolated Vertex : Vertex Degree zero "Isolated Vertex"
Hamiltonian and Eulerian Paths
editHamiltonian Cycles: A Hamiltonian Cycle received its name from Sir William Hamilton who first studied the travelling salesman problem. A Hamiltonian cycle is a path that visits every vertex once and only once i.e. it is a walk, in which no edge is repeated (a trail) and therefore a trail in which no vertex is repeated (a path). Note also it is a cycle, the last vertex is joined to the first.
A graph is said to be Eulerian if it is possible to traverse each edge once and only once, i.e. it has no odd vertices or it has an even number of odd vertices (semi-Eulerian). This has implications for the Königsberg problem. It may be easier to imagine this as if it is possible to trace the edges of a graph with a pencil without lifting the pencil off the paper or going over any lines.
Planar Graphs
editA planar graph is an undirected graph that can be drawn on the plane or on a sphere in such a way that no two edges cross, where an edge is drawn as a continuous curve (it need not be a straight line) from u to v.
Kuratowski proved a remarkable fact about planar graphs: A graph is planar if and only if it does not contain a subgraph homeomorphic to or to . (Two graphs are said to be homeomorphic if we can shrink some components of each into single nodes and end up with identical graphs. Informally, this means that non-planar-ness is caused by only two things—namely, having the structure of or within the graph).
Coloring Graphs
editA graph is said to be planar if it can be drawn on a plane in such way that no edges cross one another except of course for meeting at vertices
Each term, the Schedules Office in some university must assign a time slot for each final exam. This is not easy, because some students are taking several classes with finals, and a student can take only one test during a particular time slot. The Schedules Office wants to avoid all conflicts, but to make the exam period as short as possible.
We can recast this scheduling problem as a question about coloring the vertices of a graph. Create a vertex for each course with a final exam. Put an edge between two vertices if some student is taking both courses. For example, the scheduling graph might look like this: Next, identify each time slot with a color. For example, Monday morning is red, Monday afternoon is blue, Tuesday morning is green, etc.
Assigning an exam to a time slot is now equivalent to coloring the corresponding vertex. The main constraint is that adjacent vertices must get different colors; otherwise, some student has two exams at the same time. Furthermore, in order to keep the exam period short, we should try to color all the vertices using as few different colors as possible. For our example graph, three colors suffice: red, green, blue.
The coloring corresponds to giving one final on Monday morning (red), two Monday afternoon (blue), and two Tuesday morning (green)...
K Coloring
editMany other resource allocation problems boil down to coloring some graph. In general, a graph G is kcolorable if each vertex can be assigned one of k colors so that adjacent vertices get different colors. The smallest sufficient number of colors is called the chromatic number of G. The chromatic number of a graph is generally difficult to compute, but the following theorem provides an upper bound:
Theorem 1. A graph with maximum degree at most k is (k + 1)colorable.
Proof. We use induction on the number of vertices in the graph, which we denote by n. Let P(n) be the proposition that an nvertex graph with maximum degree at most k is (k + 1)colorable. A 1 vertex graph has maximum degree 0 and is 1colorable, so P(1) is true.
Now assume that P(n) is true, and let G be an (n + 1)vertex graph with maximum degree at most k. Remove a vertex v, leaving an nvertex graph G . The maximum degree of G is at most k, and so G is (k + 1)colorable by our assumption P(n). Now add back vertex v. We can assign v a color different from all adjacent vertices, since v has degree at most k and k + 1 colors are available. Therefore, G is (k + 1)colorable. The theorem follows by induction.
Weighted Graphs
editA weighted graph associates a label (weight) with every edge in the graph. Weights are usually real numbers, and often represent a "cost" associated with the edge, either in terms of the entity that is being modeled, or an optimization problem that is being solved.
Recursion
editIn this section we will look at certain mathematical processes which deal with the fundamental property of recursion at its core.
What is Recursion?
editRecursion, simply put, is the process of describing an action in terms of itself. This may seem a bit strange to understand, but once it "clicks" it can be an extremely powerful way of expressing certain ideas.
Let's look at some examples to make things clearer.
Exponents
editWhen we calculate an exponent, say x3, we multiply x by itself three times. If we have x5, we multiply x by itself five times.
However, if we want a recursive definition of exponents, we need to define the action of taking exponents in terms of itself. So we note that x4 for example, is the same as x3 × x. But what is x3? x3 is the same as x2 × x. We can continue in this fashion up to x0=1. What can we say in general then? Recursively,
- xn = x × (xn-1)
with the fact that
- x0=1
We need the second fact because the definitions fail to make sense if we continue with negative exponents, and we would continue indefinitely!
Recursive definitions
editReducing the problem into same problem by smaller inputs. for example
a power n
2 power 4
the recursion(smaller inputs) of this function is = 2.2.2.2.1
for this we declare some recursive definitions
a=2
n=4
f(0)=1
f(1)=2
f(2)=2
f(3)=2
f(4)=2
for this recursion we form a formula f(n)= a.f(n-1)
by putting these smaller values we get the same answer.
Recurrence relations
editIn mathematics, we can create recursive functions, which depend on its previous values to create new ones. We often call these recurrence relations.
For example, we can have the function :f(x)=2f(x-1), with f(1)=1 If we calculate some of f's values, we get
- 1, 2, 4, 8, 16, ...
However, this sequence of numbers should look familiar to you! These values are the same as the function 2x, with x = 0, 1, and so on.
What we have done is found a non-recursive function with the same values as the recursive function. We call this solving also know as x'to sup with value 0 and so on.
Linear recurrence relations
editWe will look especially at a certain kind of recurrence relation, known as linear.
Here is an example of a linear recurrence relation:
- f(x)=3f(x-1)+12f(x-2), with f(0)=1 and f(1)=1
Instead of writing f(x), we often use the notation an to represent a(n), but these notations are completely interchangeable.
Note that a linear recurrence relation should always have stopping cases, otherwise we would not be able to calculate f(2), for example, since what would f(1) be if we did not define it? These stopping cases when we talk about linear recurrence relations are known as initial conditions.
In general, a linear recurrence relation is in the form
- an=A1an-1 + A2an-2 + ... + Ajan-j
- with f(t1)=u1, f(t2)=u2, ..., f(tj)=uj as initial conditions.
The number j is important, and it is known as the order of the linear recurrence relation. Note we always need at least j initial conditions for the recurrence relation to make sense.
Recall in the previous section we saw that we can find a nonrecursive function (a solution) that will take on the same values as the recurrence relation itself. Let's see how we can solve some linear recurrence relations - we can do so in a very systematic way, but we need to establish a few theorems first.
Solving linear recurrence relations
editSum of solutions
editThis theorem says that:
- If f(n) and g(n) are both solutions to a linear recurrence relation an=Aan-1+Ban-2, their sum is a solution also.
This is true, since if we rearrange the recurrence to have an-Aan-1-Ban-2=0 And we know that f(n) and g(n) are solutions, so we have, on substituting into the recurrence
- f(n)-Af(n-1)-Bf(n-2)=0
- g(n)-Ag(n-1)-Bg(n-2)=0
If we substitute the sum f(n)+g(n) into the recurrence, we obtain
- (f(n)+g(n))-A(f(n-1)+g(n-1))-B((f(n-2)+g(n-2))=0
On expanding out, we have
- f(n)-Af(n-1)-Bf(n-2)+g(n)-Ag(n-1)-Bg(n-2)
But using the two facts we established first, this is the same as
- 0+0=0
So f(n)+g(n) is indeed a solution to the recurrence.
General solution
editThe next theorem states that:
- Say we have a second-order linear recurrence relation, an-Aan-1-Ban-2=0, with supplied initial conditions.
Then γrn is a solution to the recurrence, where r is a solution of the quadratic equation
- x2-Ax-B=0
which we call the characteristic equation.
We guess (it doesn't matter why, accept it for now) that γrn may be a solution. We can prove that this is a solution IF (and only if) it solves the characteristic equation ;
We substitute γrn (r not zero) into the recurrence to get
- γrn-Aγrn-1-Bγrn-2=0
then factor out by γrn-2, the term farthest on the right
- γrn-2(r2-Ar-B)=0
and we know that r isn't zero, so rn-2 can never be zero. So r2-Ar-B must be zero, and so γrn, with r a solution of r2-Ar-B=0, will indeed be a solution of the linear recurrence. Please note that we can easily generalize this fact to higher order linear recurrence relations.
Where did this come from? Why does it work (beyond a rote proof)? Here's a more intuitive (but less mathematically rigorous) explanation.
Solving the characteristic equation finds a function that satisfies the linear recurrence relation, and conveniently doesn't require the summation of all n terms to find the nth one.
We want : a function F(n) such that F(n) = A * F(n-1) + B * F(n-2)
We solve : x2 = A* x + B, and call the solution(s) r. There can be more than one value of r, like in the example below!
We get : a function F(n) = rn that satisfies F(n) = A * F(n-1) + B * F(n-2)
Let's check: Does rn = A*rn-1 + B*rn-2 ? Divide both sides by rn-2 and you get r2 = A*r + B, which must be true because r is a solution to x2 = A* x + B
Why does γ*rn also satisfy the recurrence relation?
If F(n)=rn is a solution, that is, rn-A*rn-1-B*rn-2=0, then certainly F(n)=γrn is a solution since γrn-A*γrn-1-B*γrn-2=γ(rn-A*rn-1-B*rn-2)=0.
Because we have a second order recurrence, the general solution is the sum of two solutions, corresponding to the two roots of the characteristic equation. Say these are r and s. The general solution is C(rn)+D(sn) where C,D are some constants. We find them using the two (there must be two so that we can find C and D) starting values of the relation. Substituting these into the general solution will give two equations which we can (hopefully) solve.
Example
editLet's work through an example to see how we can use the above theorems to solve linear recurrence relations. Examine the function a(n) given here
- a(n)=a(n-1)+2a(n-2)
The characteristic equation of this recurrence relation is
- r2-r-2 = 0 from above, as A=1 and B=2
i.e. (r-2)(r+1)=0 which has roots 2, -1.
So the general solution is C(2n)+D(-1)n.
To find C and D for this specific case, we need two starting values, let's say a(1) = 0 and a(2) = 2. These give a system of two equations
0 = C(21)+D(-1)1
2 = C(22)+D(-1)2
Solving these two equations yields: C = 1/3 , D = 2/3, so the solution is 1/3*(2n)+2/3*(-1)n.
Functions and relations
editIntroduction
editThis article examines the concepts of a function and a relation.
A relation is any association or link between elements of one set, called the domain or (less formally) the set of inputs, and another set, called the range or set of outputs. Some people mistakenly refer to the range as the codomain(range), but as we will see, that really means the set of all possible outputs—even values that the relation does not actually use. (Beware: some authors do not use the term codomain(range), and use the term range instead for this purpose. Those authors use the term image for what we are calling range. So while it is a mistake to refer to the range or image as the codomain(range), it is not necessarily a mistake to refer to codomain as range.)
For example, if the domain is a set Fruits = {apples, oranges, bananas} and the codomain(range) is a set Flavors = {sweetness, tartness, bitterness}, the flavors of these fruits form a relation: we might say that apples are related to (or associated with) both sweetness and tartness, while oranges are related to tartness only and bananas to sweetness only. (We might disagree somewhat, but that is irrelevant to the topic of this book.) Notice that "bitterness", although it is one of the possible Flavors (codomain)(range), is not really used for any of these relationships; so it is not part of the range (or image) {sweetness, tartness}.
Another way of looking at this is to say that a relation is a subset of ordered pairs drawn from the set of all possible ordered pairs (of elements of two other sets, which we normally refer to as the Cartesian product of those sets). Formally, R is a relation if
for the domain X and codomain(range) Y. The inverse relation of R, which is written as R-1, is what we get when we interchange the X and Y values:
Using the example above, we can write the relation in set notation: {(apples, sweetness), (apples, tartness), (oranges, tartness), (bananas, sweetness)}. The inverse relation, which we could describe as "fruits of a given flavor", is {(sweetness, apples), (sweetness, bananas), (tartness, apples), (tartness, oranges)}. (Here, as elsewhere, the order of elements in a set has no significance.)
One important kind of relation is the function. A function is a relation that has exactly one output for every possible input in the domain. (The domain does not necessarily have to include all possible objects of a given type. In fact, we sometimes intentionally use a restricted domain in order to satisfy some desirable property.) The relations discussed above (flavors of fruits and fruits of a given flavor) are not functions: the first has two possible outputs for the input "apples" (sweetness and tartness); and the second has two outputs for both "sweetness" (apples and bananas) and "tartness" (apples and oranges).
The main reason for not allowing multiple outputs with the same input is that it lets us apply the same function to different forms of the same thing without changing their equivalence. That is, if f is a function with a (or b) in its domain, then a = b implies that f(a) = f(b). For example, z - 3 = 5 implies that z = 8 because f(x) = x + 3 is a function unambiguously defined for all numbers x.
The converse, that f(a) = f(b) implies a = b, is not always true. When it is, there is never more than one input x for a certain output y = f(x). This is the same as the definition of function, but with the roles of X and Y interchanged; so it means the inverse relation f-1 must also be a function. In general—regardless of whether or not the original relation was a function—the inverse relation will sometimes be a function, and sometimes not.
When f and f-1 are both functions, they are called one-to-one, injective, or invertible functions. This is one of two very important properties a function f might (or might not) have; the other property is called onto or surjective, which means, for any y ∈ Y (in the codomain), there is some x ∈ X (in the domain) such that f(x) = y. In other words, a surjective function f maps onto every possible output at least once.
A function can be neither one-to-one nor onto, both one-to-one and onto (in which case it is also called bijective or a one-to-one correspondence), or just one and not the other. (As an example which is neither, consider f = {(0,2), (1,2)}. It is a function, since there is only one y value for each x value; but there is more than one input x for the output y = 2; and it clearly does not "map onto" all integers.)
Relations
editIn the above section dealing with functions and their properties, we noted the important property that all functions must have, namely that if a function does map a value from its domain to its co-domain, it must map this value to only one value in the co-domain.
Writing in set notation, if a is some fixed value:
- |{f(x)|x=a}| ∈ {0, 1}
The literal reading of this statement is: the cardinality (number of elements) of the set of all values f(x), such that x=a for some fixed value a, is an element of the set {0, 1}. In other words, the number of outputs that a function f may have at any fixed input a is either zero (in which case it is undefined at that input) or one (in which case the output is unique).
However, when we consider the relation, we relax this constriction, and so a relation may map one value to more than one other value. In general, a relation is any subset of the Cartesian product of its domain and co-domain.
All functions, then, can be considered as relations also.
Notations
editWhen we have the property that one value is related to another, we call this relation a binary relation and we write it as
- x R y
where R is the relation.
For arrow diagrams and set notations, remember for relations we do not have the restriction that functions do and we can draw an arrow to represent the mappings, and for a set diagram, we need only write all the ordered pairs that the relation does take: again, by example
- f = {(0,0),(1,1),(-1,1),(2,2),(-2,2)}
is a relation and not a function, since both 1 and 2 are mapped to two values, (1 and -1, and 2 and -2 respectively) example let A=2,3,5;B=4,6,9 then A*B=(2,4),(2,6),(2,9),(3,4),(3,6),(3,9),(5,4),(5,6),(5,9) Define a relation R=(2,4),(2,6),(3,6),(3,9) add functions and problems to one another.
Some simple examples
editLet us examine some simple relations.
Say f is defined by
- {(0,0),(1,1),(2,2),(3,3),(1,2),(2,3),(3,1),(2,1),(3,2),(1,3)}
This is a relation (not a function) since we can observe that 1 maps to 2 and 3, for instance.
Less-than, "<", is a relation also. Many numbers can be less than some other fixed number, so it cannot be a function.
Properties
editWhen we are looking at relations, we can observe some special properties different relations can have.
Reflexive
editA relation is reflexive if, we observe that for all values a:
- a R a
In other words, all values are related to themselves.
The relation of equality, "=" is reflexive. Observe that for, say, all numbers a (the domain is R):
- a = a
so "=" is reflexive.
In a reflexive relation, we have arrows for all values in the domain pointing back to themselves:
Note that ≤ is also reflexive (a ≤ a for any a in R). On the other hand, the relation < is not (a < a is false for any a in R).
Symmetric
editA relation is symmetric if, we observe that for all values of a and b:
- a R b implies b R a
The relation of equality again is symmetric. If x=y, we can also write that y=x also.
In a symmetric relation, for each arrow we have also an opposite arrow, i.e. there is either no arrow between x and y, or an arrow points from x to y and an arrow back from y to x:
Neither ≤ nor < is symmetric (2 ≤ 3 and 2 < 3 but neither 3 ≤ 2 nor 3 < 2 is true).
Transitive
editA relation is transitive if for all values a, b, c:
- a R b and b R c implies a R c
The relation greater-than ">" is transitive. If x > y, and y > z, then it is true that x > z. This becomes clearer when we write down what is happening into words. x is greater than y and y is greater than z. So x is greater than both y and z.
The relation is-not-equal "≠" is not transitive. If x ≠ y and y ≠ z then we might have x = z or x ≠ z (for example 1 ≠ 2 and 2 ≠ 3 and 1 ≠ 3 but 0 ≠ 1 and 1 ≠ 0 and 0 = 0).
In the arrow diagram, every arrow between two values a and b, and b and c, has an arrow going straight from a to c.
Antisymmetric
editA relation is antisymmetric if we observe that for all values a and b:
- a R b and b R a implies that a=b
Notice that antisymmetric is not the same as "not symmetric."
Take the relation greater than or equal to, "≥" If x ≥ y, and y ≥ x, then y must be equal to x. a relation is anti-symmetric if and only if a∈A, (a,a)∈R
Trichotomy
editA relation satisfies trichotomy if we observe that for all values a and b it holds true that: aRb or bRa
The relation is-greater-or-equal satisfies since, given 2 real numbers a and b, it is true that whether a ≥ b or b ≥ a (both if a = b).
Problem set
editGiven the above information, determine which relations are reflexive, transitive, symmetric, or antisymmetric on the following - there may be more than one characteristic. (Answers follow.) x R y if
- x = y
- x < y
- x2 = y2
- x ≤ y
Answers
edit- Symmetric, Reflexive, and transitive
- Transitive, Trichotomy
- Symmetric, Reflexive, and transitive (x2 = y2 is just a special case of equality, so all properties that apply to x = y also apply to this case)
- Reflexive, Transitive and Antisymmetric (and satisfying Trichotomy)
Equivalence relations
editWe have seen that certain common relations such as "=", and congruence (which we will deal with in the next section) obey some of these rules above. The relations we will deal with are very important in discrete mathematics, and are known as equivalence relations. They essentially assert some kind of equality notion, or equivalence, hence the name.
Characteristics of equivalence relations
editFor a relation R to be an equivalence relation, it must have the following properties, viz. R must be:
- symmetric
- transitive
- reflexive
(A helpful mnemonic, S-T-R)
In the previous problem set you have shown equality, "=", to be reflexive, symmetric, and transitive. So "=" is an equivalence relation.
We denote an equivalence relation, in general, by .
Example proof
editSay we are asked to prove that "=" is an equivalence relation. We then proceed to prove each property above in turn (Often, the proof of transitivity is the hardest).
- Reflexive: Clearly, it is true that a = a for all values a. Therefore, = is reflexive.
- Symmetric: If a = b, it is also true that b = a. Therefore, = is symmetric
- Transitive: If a = b and b = c, this says that a is the same as b which in turn is the same as c. So a is then the same as c, so a = c, and thus = is transitive.
Thus = is an equivalence relation.
Partitions and equivalence classes
editIt is true that when we are dealing with relations, we may find that many values are related to one fixed value.
For example, when we look at the quality of congruence, which is that given some number a, a number congruent to a is one that has the same remainder or modulus when divided by some number n, as a, which we write
- a ≡ b (mod n)
and is the same as writing
- b = a+kn for some integer k.
(We will look into congruences in further detail later, but a simple examination or understanding of this idea will be interesting in its application to equivalence relations)
For example, 2 ≡ 0 (mod 2), since the remainder on dividing 2 by 2 is in fact 0, as is the remainder on dividing 0 by 2.
We can show that congruence is an equivalence relation (This is left as an exercise, below Hint use the equivalent form of congruence as described above).
However, what is more interesting is that we can group all numbers that are equivalent to each other.
With the relation congruence modulo 2 (which is using n=2, as above), or more formally:
- x ~ y if and only if x ≡ y (mod 2)
we can group all numbers that are equivalent to each other. Observe:
This first equation above tells us all the even numbers are equivalent to each other under ~, and all the odd numbers under ~.
We can write this in set notation. However, we have a special notation. We write:
- [0]={0,2,4,...}
- [1]={1,3,5,...}
and we call these two sets equivalence classes.
All elements in an equivalence class by definition are equivalent to each other, and thus note that we do not need to include [2], since 2 ~ 0.
We call the act of doing this 'grouping' with respect to some equivalence relation partitioning (or further and explicitly partitioning a set S into equivalence classes under a relation ~). Above, we have partitioned Z into equivalence classes [0] and [1], under the relation of congruence modulo 2.
Problem set
editGiven the above, answer the following questions on equivalence relations (Answers follow to even numbered questions)
- Prove that congruence is an equivalence relation as before (See hint above).
- Partition {x | 1 ≤ x ≤ 9} into equivalence classes under the equivalence relation
Answers
edit2. [0]={6}, [1]={1,7}, [2]={2,8}, [3]={3,9}, [4]={4}, [5]={5}
Partial orders
editWe also see that "≥" and "≤" obey some of the rules above. Are these special kinds of relations too, like equivalence relations? Yes, in fact, these relations are specific examples of another special kind of relation which we will describe in this section: the partial order.
As the name suggests, this relation gives some kind of ordering to numbers.
Characteristics of partial orders
editFor a relation R to be a partial order, it must have the following three properties, viz R must be:
- reflexive
- antisymmetric
- transitive
(A helpful mnemonic, R-A-T)
We denote a partial order, in general, by .
Question:
- Suppose R is a relation on a set of integers Z then prove that R is a partial order relation on Z iff a=b raise to power r.
Example proof
editSay we are asked to prove that "≤" is a partial order. We then proceed to prove each property above in turn (Often, the proof of transitivity is the hardest).
Reflexive
editClearly, it is true that a ≤ a for all values a. So ≤ is reflexive.
Antisymmetric
editIf a ≤ b, and b ≤ a, then a must be equal to b. So ≤ is antisymmetric
Transitive
editIf a ≤ b and b ≤ c, this says that a is less than b and c. So a is less than c, so a ≤ c, and thus ≤ is transitive.
Thus ≤ is a partial order.
Problem set
editGiven the above on partial orders, answer the following questions
- Prove that divisibility, |, is a partial order (a | b means that a is a factor of b, i.e., on dividing b by a, no remainder results).
- Prove the following set is a partial order: (a, b) (c, d) implies ab≤cd for a,b,c,d integers ranging from 0 to 5.
Answers
edit2. Simple proof; Formalization of the proof is an optional exercise.
- Reflexivity: (a, b) (a, b) since ab=ab.
- Antisymmetric: (a, b) (c, d) and (c, d) (a, b) since ab≤cd and cd≤ab imply ab=cd.
- Transitive: (a, b) (c, d) and (c, d) (e, f) implies (a, b) (e, f) since ab≤cd≤ef and thus ab≤ef
Posets
editA partial order imparts some kind of "ordering" amongst elements of a set. For example, we only know that 2 ≥ 1 because of the partial ordering ≥.
We call a set A, ordered under a general partial ordering , a partially ordered set, or simply just poset, and write it (A, ).
Terminology
editThere is some specific terminology that will help us understand and visualize the partial orders.
When we have a partial order , such that a b, we write to say that a but a ≠ b. We say in this instance that a precedes b, or a is a predecessor of b.
If (A, ) is a poset, we say that a is an immediate predecessor of b (or a immediately precedes b) if there is no x in A such that a x b.
If we have the same poset, and we also have a and b in A, then we say a and b are comparable if a b or b a. Otherwise they are incomparable.
Hasse diagrams
editHasse diagrams are special diagrams that enable us to visualize the structure of a partial ordering. They use some of the concepts in the previous section to draw the diagram.
A Hasse diagram of the poset (A, ) is constructed by
- placing elements of A as points
- if a and b ∈ A, and a is an immediate predecessor of b, we draw a line from a to b
- if a b, put the point for a lower than the point for b
- not drawing loops from a to a (this is assumed in a partial order because of reflexivity)
Operations on Relations
editThere are some useful operations one can perform on relations, which allow to express some of the above mentioned properties more briefly.
Inversion
editLet R be a relation, then its inversion, R-1 is defined by
R-1 := {(a,b) | (b,a) in R}.
Concatenation
editLet R be a relation between the sets A and B, S be a relation between B and C. We can concatenate these relations by defining
R • S := {(a,c) | (a,b) in R and (b,c) in S for some b out of B}
Diagonal of a Set
editLet A be a set, then we define the diagonal (D) of A by
D(A) := {(a,a) | a in A}
Shorter Notations
editUsing above definitions, one can say (lets assume R is a relation between A and B):
R is transitive if and only if R • R is a subset of R.
R is reflexive if and only if D(A) is a subset of R.
R is symmetric if R-1 is a subset of R.
R is antisymmetric if and only if the intersection of R and R-1 is D(A).
R is asymmetric if and only if the intersection of D(A) and R is empty.
R is a function if and only if R-1 • R is a subset of D(B).
In this case it is a function A → B. Let's assume R meets the condition of being a function, then
R is injective if R • R-1 is a subset of D(A).
R is surjective if {b | (a,b) in R} = B.
Functions
editA function is a relationship between two sets of numbers. We may think of this as a mapping; a function maps a number in one set to a number in another set. Notice that a function maps values to one and only one value. Two values in one set could map to one value, but one value must never map to two values: that would be a relation, not a function.

|
For example, if we write (define) a function as:
then we say:
- 'f of x equals x squared'
and we have
and so on.
This function f maps numbers to their squares.
Range and codomain
editIf D is a set, we can say
which forms a née of f is usually a subset of a larger set. This set is known as the codomain of a function. For example, with the function f(x)=cos x, the range of f is [-1,1], but the codomain is the set of real numbers.
Notations
editWhen we have a function f, with domain D and range R, we write:
If we say that, for instance, x is mapped to x2, we also can add
Notice that we can have a function that maps a point (x,y) to a real number, or some other function of two variables -- we have a set of ordered pairs as the domain. Recall from set theory that this is defined by the Cartesian product - if we wish to represent a set of all real-valued ordered pairs we can take the Cartesian product of the real numbers with itself to obtain
- .
When we have a set of n-tuples as part of the domain, we say that the function is n-ary (for numbers n=1,2 we say unary, and binary respectively).
Other function notation
editFunctions can be written as above, but we can also write them in two other ways. One way is to use an arrow diagram to represent the mappings between each element. We write the elements from the domain on one side, and the elements from the range on the other, and we draw arrows to show that an element from the domain is mapped to the range.
For example, for the function f(x)=x3, the arrow diagram for the domain {1,2,3} would be:

Another way is to use set notation. If f(x)=y, we can write the function in terms of its mappings. This idea is best to show in an example.
Let us take the domain D={1,2,3}, and f(x)=x2. Then, the range of f will be R={f(1),f(2),f(3)}={1,4,9}. Taking the Cartesian product of D and R we obtain F={(1,1),(2,4),(3,9)}.
So using set notation, a function can be expressed as the Cartesian product of its domain and range.
f(x)
This function is called f, and it takes a variable x. We substitute some value for x to get the second value, which is what the function maps x to.
Types of functions
editFunctions can either be one to one (injective), onto (surjective), or bijective.
INJECTIVE Functions are functions in which every element in the domain maps into a unique elements in the codomain.
SURJECTIVE Functions are functions in which every element in the codomain is mapped by an element in the domain.
'BIJECTIVE Functions are functions that are both injective and surjective.
---onto functions a function f form A to B is onto ,
Semigroup
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
In this section we Define a simple mathematical system, consisting of a set together with a binary operation that has many Important application.
Semi group
editLet (A,*) be algebraic structure, where * is any binary operation on A. Then, the system (A,*) is semi-group if it satisfies the following properties: 1. The operation * is a closed operation on set A. 2. The operation * is an associative operation.
Upper-level discrete mathematics
editUpper-level set theory
editAxiomatic set theory
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
See also: Topology/Set Theory
Zermelo-Frankel Axioms
editIntroduction
editZermelo–Fraenkel set theory, with the axiom of choice, commonly abbreviated ZFC, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics.
ZFC consists of a single primitive notion, that of set, and a single assumption, namely that all mathematical objects are sets. There is a single primitive binary relation, set membership; that set a is a member of set b is written (usually read "a is an element of b" or "a is in b"). The axioms of ZFC govern how sets behave and interact.
The axioms
edit1. Axiom of extensionality: Two sets are equal (are the same set) if they have the same elements.
The converse of this axiom follows from the substitution property of equality. If the background logic does not include equality "=", x=y may be defined as abbreviating ∀z[z∈x↔z∈y] ∧ ∀z[x∈z↔y∈z], in which case this axiom can be reformulated as — if x and y have the same elements, then they belong to the same sets.
2. Axiom of regularity (also called the Axiom of foundation): Every non-empty set x contains a member y such that x and y are disjoint sets.
3. Axiom schema of specification (also called the axiom schema of separation or of restricted comprehension): If z is a set, and is any property which may characterize the elements x of z, then there is a subset y of z containing those x in z which satisfy the property. More formally:
The axiom of specification can be used to prove the existence of the empty set, denoted , once the existence of at least one set is established (see above). A common way to do this is to use an instance of specification for a property which all sets do not have. For example, if w is a set which already exists, the empty set can be constructed as
- .
If the background logic includes equality, it is also possible to define the empty set as
- .
Thus the axiom of the empty set is implied by the nine axioms presented here. The axiom of extensionality implies the empty set is unique, if it exists. It is common to make a definitional extension that adds the symbol to the language of ZFC.
4. Axiom of pairing: If x and y are sets, then there exists a set which contains x and y as elements.
5. Axiom of union: For any set there is a set A containing every set that is a member of some member of
6. Axiom schema of collection: This axiom states that if the domain of a function f is a set, and f(x) is a set for any x in that domain, then the range of f is a subclass of a set, subject to a restriction needed to avoid paradoxes.
7. Axiom of infinity: Let abbreviate , where is some set. Then there exists a set X such that the empty set is a member of X and, whenever a set y is a member of X, then is also a member of X.
More colloquially, there exists a set X having infinitely many members.
8. Axiom of power set: Let abbreviate For any set x, there is a set y which is a superset of the power set of x. The power set of x is the class whose members are every possible subset of x.
Alternative forms of axioms 1–8 are often encountered. Some ZF axiomatizations include an axiom asserting that the empty set exists. The axioms of pairing, union, replacement, and power set are often stated so that the members of the set x whose existence is being asserted, are just those sets which the axiom asserts x must contain.
9. Well-ordering theorem: For any set X, there is a binary relation R which well-orders X. This means R is a linear order on X such that every nonempty subset of X has a member which is minimal under R.
Given axioms 1-8, there are many statements provably equivalent to axiom 9, the best known of which is the axiom of choice (AC), which goes as follows. Let X be a set whose members are all non-empty. Then there exists a function f, called a "choice function," whose domain is X, and whose range is a set, called the "choice set," each member of which is a single member of each member of X. Since the existence of a choice function when X is a finite set is easily proved from axioms 1-8, AC only matters for certain infinite sets. AC is characterized as nonconstructive because it asserts the existence of a choice set but says nothing about how the choice set is to be "constructed." Much research has sought to characterize the definability (or lack thereof) of certain sets whose existence AC asserts.
Topoi
editUpper-level number theory
editNumber representations
editIntroduction
editYou are already familiar with writing a number down, and having it mean a certain combination of tens, hundreds, and so on. This is one form of number representation, but there are others. We will look at number bases and continued fractions.
Number bases
editYou are already familiar with base-10 number representation. For example, the number 2818 is the same as
- 2×103+8×102+1×101+8×100
We can replace the number 10 here with any number and we obtain a different number. In general, we can represent an integer n in a base b by the following:
- akbk+ak-1bk-1+...+a0b0
where the ai are all less than b.
We write a number base b as (akak-1...a0)b.
For example, if we have the numeral 243 in base 6, we write it (243)6. When we are in base 10 we simply write the number: for example the numeral 155 in base 10 is simply written 155.
However, given a number in a base b, how can we convert it to our natural base 10 system? Likewise, how can we convert a number from our base 10 system to base b?
The first is relatively easy, the other more difficult.
Converting base b to base 10
editWe simply use the definition of a base-b number to convert a base-b number to base 10 - that is we simply multiply out.
For example
- (919)12=9×122+121+9=1317.
Converting base 10 to base b
editThis task however is slightly more difficult, and there are several ways of performing this task.
One method is to write each step using the division algorithm from the Number theory section. For example, if we wish to convert 1317 to base 12:
- 1317 = 12 × 109 + 9
- 109 = 12 × 9 + 1
- 9 = 12 × 0 + 9
So in base 12, (919)12=1317.
Real numbers
editWe've just seen how we can convert integers from base to base, but how do we work with converting real numbers?
Recall in base 10 we write a number such as 11.341 as
- 1×101+1×100+3×10-1+4×10-2+1×10-3
and so we can extend our definition above of a base-b number to be
akbk+ak-1bk-1+...+a0b0+a-1b-1+...
where the ai are all less than b, and the sum could terminate or go on indefinitely.
Again, how are we to convert these numbers from base to base? We can convert the integral part, but what about the fractional part (the part less than 1)?
Converting fractional n to base-b
editSay we wish to convert .341 in base 10 to base 6.
We write a table, using the following rules
i ci γi 6γi 0 0 .341 2.046 1 2 .046 0.276 2 0 .276 1.656 3 1 .656 3.936 4 3 .936 5.616 5 5 .616 3.696 6 3 .696 4.176 7 4 .176 1.056 8 1 .056 0.336 9 0 .336 2.016
It looks like this expansion will go on forever! We need to calculate for further values of i to see whether we hit a repeat value of γi to see whether we get a repetition.
So we have the approximation that .341 is near to (.20135341)6. (Calculate this using the definition. How close is our approximation?)
If we obtain a base-b representation for example, that looks something like (.18191819181918191819...)b we call the representation periodic. We often write this as
We use this same procedure to convert a fractional number to base-b by replacing the 6 above with b.
Converting fractional n to base 10
editWe have a nifty trick we can use to convert a fractional n in base-b to base 10 provided the representation repeats. Let us look at an example:
Consider . Now then
And now
which is
Then
And finally
On converting (3145)7 to base 10, we obtain the following
Continued fractions
editIn a sense, the base-b representation is nice, but it has a few shortcomings in respect to accuracy. We cannot reliably represent the number using base-b representation. This is where the continued fraction representation comes in handy, which has some nice properties regarding quadratic irrationals.
A continued fraction is a number in the form
Since this notation is clearly rather cumbersome, we abbreviate the above to
Again we ask ourselves how can we convert from and to this number representation? Again converting from is simpler than converting to.
Converting from continued fraction representation
editWe simply use our definition of the continued fraction to convert from a continued fraction. This may look difficult, but in fact is quite simple depending on which end one starts with. Let's look at an example
Consider
Now, we work from right to left. We first have the fraction
The next digit 2 tells us to perform
and then take the reciprocal to get
Now the next digit 1 tells us to perform
and then to take the reciprocal to get
Now we must add q0 which is always greater than 1 and we get the result:
Converting to continued fraction representation
editAgain, we draw up a table.
Consider the fraction 12/22, and use the following rules in the table
i θi θi-1 qi 0 12/22 . 0 1 12/22 22/12 1 2 5/6 6/5 1 3 1/5 5/1 5
(stop since next row will be full of 0s)
So now the continued fraction for 12/22 is [0; 1, 1, 5].
Converting a periodic continued fraction to quadratic irrational
editFirstly, we make note of a nice property of periodic continued fractions (where the sequence of qi repeat), that
- every periodic continued fraction is a number in the form
For example, consider the continued fraction
Now
which we can rewrite as
Now we can simplify to obtain
which is a quadratic equation and can be solved to obtain
- .
Note that we can always roll up the continued fraction into the form (aα+b)/(cα+d)=α, which demonstrates the point that every quadratic irrational has a repeating continued fraction representation
Convergents
editSay we have a continued fraction [q0; q1, ... ] which represents a number n. Let us examine the following series of fractions [q0], [q0; q1], [q0; q1, q2] and so on. Each element of the series is known as a convergent. It turns out that the series of convergents provide the best rational approximations to n.
These can be calculated from the continued fraction representation, but also from the calculation table. Let us take .
Continue as before, but place an extra -1 row, and set u-1=1, v-1=0. Iterate with the rules
and the sequence repeats and the continued fraction is [2; 2, 4, 2, 4, ... ]. We can continue the process to generate more convergents - the convergents are 2, 5/2, 22/9, 49/20, ...
Modular arithmetic
editIntroduction
editWe have already considered moduli and modular arithmetic back in Number theory, however in this section we will take a more in depth view of modular arithmetic.
For revision, you should review the material in number theory if you choose.
Simultaneous equations
editWhen we speak of simultaneous equations with relation to modular arithmetic, we are talking about simultaneous solutions to sets of equations in the form
- x ≡ a1 (mod m1)
- :
- :
- x ≡ ak (mod mk)
There are two principal methods we will consider, successive substitution and the Chinese remainder theorem.
Successive substitution
editThe method of successive substitution is that where we use the definition of the modulus to rewrite these simultaneous equations, and then successively make substitutions.
It will probably be best to motivate the idea with an example.
Example: Solve 3x ≡ 10 (mod 19), and x ≡ 19 (mod 21) using successive substitution.
First:
- 3x ≡ 10 (mod 19)
Find the inverse of 3 in Z19; 3-1=-6, then
- x ≡ -60 (mod 19)
- x ≡ 16 (mod 19)
- x = 16 + 19j ∃ j∈Z (*)
Substitute in the second equation
- (16+19j) ≡ 19 (mod 21)
- 19j ≡ 3 (mod 21)
Find the inverse of 19 in Z21; 19-1=10
- j = 30 (mod 21)
- j = 9 (mod 21)
Writing in the equivalent form
- j = 9 + 21k ∃ k∈Z
Substituting back j in (*)
- x = 16 + 19(9+21k)
- x = 187+399k
Writing back in the first form
- x ≡ 187 (mod 399)
which is our solution.
Chinese remainder theorem
editThe Chinese remainder theorem is a method for solving simultaneous linear congruences when the moduli are coprime.
Given the equations
- x ≡ a1 (mod m1)
- :
- :
- x ≡ ak (mod mk)
multiply the moduli together, i.e. N=m1m2...mk, then write n1=N/m1, ..., nk=N/mk.
We then set yi be the inverse of ni mod mi for all i, so yini=1 mod mi.
Our solution will be
- x ≡ a1y1n1+...+akyknk (mod N)
To see why this works consider what values x mod mk takes. The term akyknk mod mk becomes equal to ak as yknk=1 mod mk, and all the terms ajyjnj mod mk become equal to zero as when mk is a factor of nj.
The Chinese Remainder Theorem is of immense practical use, as if we wish to solve an equation mod M for some large M, we can instead solve it mod p for every prime factor of M and use CRT to obtain a solution mod M.
Powers and roots
editThis section deals with looking powers of numbers modulo some modulus. We look at efficient ways of calculating
- ab (mod m)
If we tried to calculate this normally - by calculating ab and then taking the modulus - it would take an exorbitant amount of time. However some of the theory behind modular arithmetic allows us a few shortcuts.
We will look at some of these and the theory involved with them.
Fermat's (little) Theorem
editFermat's theorem allows us to see where ab (mod m) is 1. This has an application in disproving primality.
It states
- If p is prime, and gcd(a,p)=1, then, in Zp
- ap-1=1.
So, for example, 1310=1 in Z11.
Primitive elements
editIf in Zn, can we write some elements as powers of an element? This is conceivably possible.
Let's look at Z3.
- 20=1
- 21=2
- 22=1
The elements {1,2} constitute in fact :Z3*.
Generally, we have
- If p prime, then there is an element g∈Zp* such that every element of Zp* is a power of g.
Orders
editWe can express this idea in a different way, using the concept of the order. We denote the order of a ∈ Zn* by the smallest integer k written On(a) such that
- ak=1 in Zn.
For example, On(-1)=2 for all n except 2, since
- (-1)2=1
except when n = 2, since in that field -1 = 1 and thus has order 1.
Note if gcd(a,n)≠1, that is, a ∉ Zn*, the order is not defined.
Properties of orders
editThe orders obey some properties, the first of which was originally proven by Lagrange:
If p prime, gcd(a,p)=1,
- Op(a) divides p-1
- a is primitive iff Op(a)=p-1
Orders and finding primitive elements
editGiven these facts above, we can find primitive elements in Zp for p > 2 fairly easily.
Using the above facts, we only need to check a(p-1)/pi=xi in Zp for all i, where the pi are the prime factors of p-1. If any of the xi are 1, a is not a primitive element, if none are, it is.
Example: Find a primitive element of Z11.
Try 2. p-1 = 10 = 2 . 5 Check:
- 210/2=25=10
- 210/5=22=4
Neither is 1, so we can say that 2 is a primitive element in Z11.
Problem set
editGiven the above, answer the following. (Answers follow to even-numbered questions)
- Is 4 primitive in Z13?
- Is 5 primitive in Z23?
- Find a primitive element of Z5.
- Find a primitive element of Z19.
Answers
edit- 2. Yes: In Z23, (23-1)=2*11, and 522/11=2, 522/2=22 and then 522=1. No lesser base gives this.
- 4. 2. Check: (19-1) has distinct prime factors 2 and 3. In Z19, 218/2≠1 and 218/3≠1 but 218=1 so 2 is primitive.
Euler's totient function
editEuler's totient function is a special function that allows us to generalize Fermat's little theorem above.
It is defined as
- φ(n) = |Zn*|
- =|{a∈Z|1 ≤ a ≤ n and gcd(a,n) = 1}|
- that is the number of elements that have inverses in Zn
Some results
editWe have the following results leading on from previous definitions.
- φ(p) = p - 1
- φ(pk) = pk-pk-1
- φ(mn)=φ(m)φ(n) for gcd(m,n)=1
- For any integer n, the sum of the totient values of each of its divisors equals n.
In other symbols: .
Proof of 2.: There are pk elements in Zpk. The non-invertible elements in Zpk are the multiples of p and there are pk-1 of them: p, 2p, 3p, ..., (pk-1-1)p, pk. Removing the non-invertible elements from the invertible ones leaves pk-pk-1 left. ∎
Corollary to 1, 2 and 3:
If n has distinct prime factors (i.e. not counting powers) pi for i=1,...,r we have
For example:
- 16=24, so φ(16)=(16)(1-1/2)=16/2=8
- φ(11)=(11)(1-1/11)=(11)(10/11)=10
- (confirm from before 11 prime so φ(11)=11-1=10).
Proof of 3.: We can prove this equality using a special case of the Chinese Remainder Theorem, where the CRT is now just a system of 2 congruences, namely:
- x == a1 (mod m)
- x == a2 (mod n)
(remember that the CRT is applicable here because m and n are assumed coprime in the equality).
Note that a1 can take on m values (from 0 to m-1), and a2 can take on n values (from 0 to n-1). Also note that, for each and everyone of the m*n (a1, a2) tuples, there is a unique solution x that is strictly smaller than m*n. Moreover, for each x strictly smaller than m*n, there is a unique tuple (a1, a2) verifying the congruence system (these two assertions are a component of the Chinese Remainder Theorem: a solution to the congruence system is unique modulo m*n).
With this bijective uniqueness property in mind, the proof is simple. Go through each x, from 0 to m*n-1, and show that if x is a totient of m*n (i.e., gcd (x,m*n) = 1), then a1 is a totient of m and a2 is a totient of n. Furthermore, you must also show that if a1 and a2 are totients of m and n respectively, then it follows that x must be a totient of m*n.
If gcd (x,m*n) = 1, then according to Bezout's identity, there exist X and Y integers such that x*X + m*n*Y = 1. Furthermore, we have:
- x = a1 + k*m
- x = a2 + q*n
Therefore, a1*X + m*(k + n*Y) = 1,
should this be a1*X + m*(k*X + n*Y) = 1 ??
so gcd (a1,m) = 1, and therefore a1 is a totient of m. Proceed similarly to prove that a2 is a totient of n.
Proving the other direction is very similar in that it requires some simple replacement algebra.
So what have we shown? In the above we have shown that for every totient x of m*n, there is a unique tuple of totients of m on the one hand and n on the other hand. Furthermore, that for each tuple of totients of m on the one hand and n on the other hand, there is a unique totient of m*n. Therefore, phi(m*n) = phi(m)*phi(n).
Proof of 4.: Let Q(g) be the set of all integers between 1 and n inclusive, such that gcd(x,n) = g. Q(g) is nonempty if and only if g divides n. If g doesn't divide n, then good luck finding an x such that g is the greatest common DIVISOR of x and n. Secondly, if x belongs to Q(g) for a given g, then it can't belong to another Q(...), since, if n is fixed, then gcd(x,n) is unique, by definition of the GREATEST common divisor. Thirdly, for all x between 1 and n inclusive, there exists a g such that gcd (x,n) = g (in the "worst" case, it's 1). Put together, these three properties imply that the union of all the Q(g) sets (for each g a divisor of n), which are pairwise mutually exclusive, is the set {1,2,3,...,n}. And therefore, the sum of the cardinalities of each Q(g) equals n.
Now we show that |Q(g)| = φ(n/g).
One direction: Let x be an arbitrary member of Q(g) for some g. Therefore, we have that gcd (x,n) = g => gcd (x/g, n/g) = 1 => x/g belongs to the set of numbers coprime to n/g (whose cardinality of course is φ(n/g)). For diff\ erent x's, the two values x1/g and x2/g are distinct. So for each x in Q(g), there is a correspondingly unique x/g in the set of numbers coprime to n/g.
Other direction: Let x be an arbitrary member of the set of numbers coprime to n/g. This implies gcd (x,n/g) = 1 => gcd (xg,n) = g => xg belongs to Q(g). For different x's, the two values x1g and x2g are distinct. So for each x in the set of numbers coprime to n/g, there is a correspondingly unique xg in Q(g).
Therefore, |Q(g)| = φ(n/g).
Euler's theorem
editWe can now generalize Fermat's theorem to extend past just Zn.
Euler's theorem says:
- If a ∈ Zn*, in Zn*,
- aφ(n)=1
- equivalently if gcd(a,n)=1,
- aφ(n)≡1 (mod n)
Example: Find 3216 in Z14. We need to calculate firstly φ(14)=φ(7)φ(2)=(7-1)(2-1)=6. Then write the exponent as: 216 = 6 × 36 So: 3216=(36)36
But Euler's theorem tells us 36=1 in Z14 (i.e., mod 14) since 3φ(14)=1 in Z14 as above. So we have: 3216=136=1.
Calculating large powers efficiently
editWhen Euler's or Fermat's theorem fails us in the calculation of a high power, there is a way to decompose an exponent down so calculation is still easy.
Let us work through an example as motivation.
Example. 528 in Z4.
First write 28 in base 2 = (11100)2 = 24+23+22 = 16 + 8 + 4
Now 528 = 516+8+4 = 516 58 54 Now rewrite these powers of 2 as repeated exponents:
- (((52)2)2)2 × ((52)2)2 × (52)2
When you calculate each exponent, reduce mod 4 each time.
Problem set
editGiven the above, calculate the following powers. (Answers follow to even-numbered questions)
- 312 (mod 13)
- 242 (mod 43)
- 6168 (mod 30)
- 2252 (mod 19)
- 261 (mod 22)
- 813 (mod 5)
- 1110 (mod 11) (Tricky!)
Answers
edit- 2. Since gcd(2,43)=1 and the exponent is one less than the modulus, use Fermat's theorem - the answer is 1
- 4. Observe that φ(19)=18 and 18|252. 252/18=14. Decompose the exponent then as 218×14=(218)14=1.
- 6. Use fast exponentiation by squaring: the answer is 3
Polynomials
editIntroduction
editIn this section we look at the polynomial in some commutative ring with identity. What is interesting is that studying polynomials over some commutative ring with identity acts very much like numbers; the same rules often are obeyed by both.
Definitions
editA polynomial over some commutative ring with identity R is an expression in the form
and n ∈ N, and x is some indeterminate (not a variable).
Terminology
editGiven the first nonzero term in the polynomial, i.e. the term anxn above:
- an is called the leading coefficient
- Given 7x3+2x+5 , 7 is the leading coefficient
- the polynomial has degree n
- 7x3+2x+5 , 3 is the degree
- if an=1 the polynomial is termed monic
- 7x3+2x+5 is not monic, whereas x4 and x5-3x+2 are monic.
In the above, if ai=0 for all i, the polynomial is the zero polynomial.
Properties
editLet R[x] be the set of all polynomials of all degrees. Clearly R is closed under addition and multiplication (although in a non-straightforward way), and thus we have that R[x] is itself a commutative ring with identity.
Assume now R is a field F; we do this so we can define some useful actions on polynomials
Division algorithm
editFirstly recall the division algorithm for numbers, that each number can be decomposed into the form
- n = qk+r
where q is the quotient and r the remainder and r<n.
Now, since we have that F is a field, we can do something similar with the polynomials over F, F[x].
If f(x), g(x) ∈ F[x], with g(x) nonzero:
- f(x) = q(x)g(x)+r(x)
Again, q(x) is known as the quotient polynomial and r(x) the remainder polynomial. Furthermore, we have the degree of r(x) ≤ degree of f(x)
We perform divisions by polynomial long division. For brevity we omit the xk terms. Here's an example. We divide x3+x+2 by x-1. First write:
Note we place a 0 in any polynomial not present. Now x3/x = x2, so we place a 1 in the second column to get
Multiply x2 throughout the divisor x-1 to get x3-x2, which is (1 -1), so write this below like the following:
Now subtract (1 0) and (1 -1), drop the third 1 to get:
Now repeat, but divide by x2 now (since we have subtracted and gotten (1 1) - x2 + x), and continue in the same fashion, to get:
So the quotient is x2+x+2, and the remainder is 4.
Euclidean algorithm
editNow we have a working division algorithm for polynomials, the Euclidean algorithm, and hence the gcd of two polynomials can readily be found.
Examples
editLet's use a similar example above: what is gcd(x3+x+2, x-1)? We've shown already above that x3+x+2=(x2+x+2)(x-1) + 4
Proceeding in the normal fashion in the Euclidean algorithm
- x3+x+2=(x2+x+2)(x-1) + 4
- gcd(x3+x+2, x-1) = gcd(x-1,4)
and the greatest common divisor of any monomial and an integer is clearly 1, so x3+x+2 and x-1 are coprime.
For a second example, consider gcd(x2-1,x2+2x+1)
- x2+2x+1=(x2-1)*1+2x+2
- x2-1=(2x+2)*x/2+ -(x+1)
- 2x+2=-(x+1)*(-2)+0
Since factors of -1 make no difference, gcd(x2-1,x2+2x+1) is -(x+1)
Irreducibles
editWe've seen that x3+x+2 and x-1 are coprime; they have no factors in common. So, are we able to determine "prime" polynomials? Indeed we can - depending on the field that the polynomial lies in. We call these irreducibles instead of primes.
Example
editTake p(x)=x3 + x2 + 2 over Z3. Now we can factor this polynomial if it has a root - from the factor theorem (which also holds for polynomials over any commutative ring with identity) p(k)=0 means k is a root. So, let's look at the following: Since we're in Z3, we luckily only need to check three values p(0)=2 p(1)=1 p(2)=2 So we have p(x) having no roots - it is irreducible ("prime").
Now observe an interesting fact. Take the exact same polynomial but instead over Z2. The polynomial then is equivalent to
- x3+x2+0
and thus has root p(0)=0 and thus is reducible but over Z2
So the reducibility of the polynomial depends on the field it is in.
Showing irreducibility
editThe general procedure to show a polynomial is irreducible is:
- observe its degree
- identify possible factorizations
- eliminate these factorizations
effectively a proof by cases.
For example, consider the polynomial q(x)=x4+x+2 in Z3. To prove it is irreducible, observe that q(x) could be factorized in the following ways:
- linear, irreducible cubic
- linear, linear, irreducible quadratic
- linear, linear, linear, linear
- irreducible quadratic, irreducible quadratic
So we can prove 1, 2, 3 by showing it has no linear factors. 4 is a little more difficult. Let us proceed to show it has no linear factors: Observe
- q(0)=2
- q(1)=1
- q(2)=2
So q has no linear factors. Now, we need to show that q is not the product of two irreducible quadratics.
In Z3, we have the quadratics
- {x2,x2+1,x2+x,x2+x+1,x2+x+2,x2+2,x2+2x,x2+2x+1,x2+2x+2}
We can identify the irreducible quadratics easily by inspection. We then obtain
- {x2+1, x2+x+2, x2+2x+2}
If we can show that neither of these polynomials divide q(x)=x4+x+2, we have shown q(x) is irreducible.
Let us try x2+1 first.
We have a remainder, so x2+1 doesn't divide q. On dividing the other polynomials, we all get a remainder. (Verify this for yourself as practice).
So q(x) is irreducible in Z3.
Modular arithmetic and polynomials
editSince we have a working polynomial division and factor theorem, and that polynomials appear to mimic the behaviour of the integers - can we reasonably define some sort of modular arithmetic with polynomials?
We can indeed. If we have a field Zp[x] and we wish to find all the remainders (remember, these remainders are polynomials) on dividing by some polynomial m(x), we can do so by polynomial long division.
If m(x) is irreducible, then the set of remainders as above forms a field.
Finite fields
editIntroduction
editRecall from the previous section that we considered the case where F[x]/<m(x)> analogous to modular arithmetic but with polynomials, and that when we are looking at numbers modulo n, we have a field iff Zn is a field if n is prime.
Can we say something similar about F[x]/<m(x)>? Indeed, if m(x) is irreducible then F[x]/<m(x)> is a field.
This section deals with these kinds of fields, known as a finite field.
Definitions
editWe have the object F[x]/<m(x)> where this is the set of polynomials in F[x] are divided by the polynomial m(x).
Of the elements in F[x]/<m(x)> we can easily define addition, subtraction, multiplication, division and so on normally but with a reduction modulo m(x) to get the desired remainder.
We have that F[x]/<m(x)> is a commutative ring with identity, and if m(x) is irreducible then F[x]/<m(x)> is a field.
If m(x) has degree n, then
If F is Zp (so p is prime) then
Properties
editNow remember with complex numbers C, we have "invented" the symbol i to stand for the root of the solution x2+1=0. In fact, we have C=R[x]/<x2+1>.
When we have a general finite field, we can do this also. We write this often as F[x]/<m(x)>=F(α) where α is "the root of" m(x) - we define α to be the root of m(x).
F(α) in fact is the smallest field which contains F and α.
Finite field theorems
editWe have a number of theorems associated with finite fields.
- If F is a finite field, |F|=q, then q=pk for some k 1 and p prime.
- There then is a monic irreducible polynomial m(x) with degree k such that F=Zp[x]/<m(x)>=Zp(α) with α a root of m(x) over Zp
- There is an element γ∈F such that the order (the least element n such that γn=1) of γ is q-1, so γ is primitive in F, and we can generate elements of F (not zero) from powers of γ, i.e. F={0, γ0=1, γ1, ..., γq-2, γq-1=1}
- F is a vector space with dimension k over Zp. It has basis {1, α, α2,...,αn-1} where n is the degree of m(x), so we have F={an-1αn-1+...+a0α0|ai∈F}
- If a∈F, a+...+a p times (pa) is 0.
- If m2(x) is any other irreducible polynomial of degree k over Zp then F is isomorphic (meaning basically equal to, except for a change in symbols) to Zp/<m2(x)> - so all ways of writing this field are basically the same. So there is essentially one field of size q=pk and we denote it GF(pk) (GF meaning Galois Field).
Some examples
editLet's look at a few examples that go through these ideas.
The complex numbers
editComplex numbers, briefly, are numbers in the form
where i is the solution to the equation x2+1=0
These numbers in fact form a field, however it is not a finite field.
Take m(x)=x2+1, with the field F being R. Then we can form the complex numbers as F/<m(x)>. Now F/<m(x)> = { a+bx | a, b ∈ R} because the remainders must be of degree less than m(x) - which is 2.
So then (a+bx)(c+dx)=ac+bdx2+(ad+bc)x.
But remember that we are working in F/<m(x)>. So x2 modulo x2+1, can be written as (x2+1)-1=-1, and substituting -1 above yields a rather familiar expression.
If we let the symbol i to be the "root of x2+1", then i2+1=0 and i2=-1. The rest of the field axioms follow from here. We can then say the complex numbers C=R/<x2+1>=R(i).
The Zp case
editWe can still do this for some field in general. Let's take Z3 for example, and pick m(x)=x2+x+2. m(x) is irreducible - m(0)=2, m(1)=4=1, m(2)=4+2+2=8=2.
So Z3/<x2+x+2> is a finite field. Assume α is a root of m(x). Then Z3(α) = { a+bα|a, b ∈ Z3}. Since Z3/<x2+x+2> is finite, we can list out all its elements. We have the constant terms, then the α terms, then the α+constant terms, and so on. We have {0, 1, 2, α, α+1, α+2, 2α, 2α+1, 2α+2}.
Now we have α2+α+2=0, then
- α2=-α-2
- α2=2α-2=2α+1
(Recall the coefficients are in Z3! We are working in Z3/<m(x)>)
We can verify multiplication works mod m(x) - for example
- (1+2α)(2+α) = 2 + α+4α+2α2
Reducing coefficients normally mod 3 we get
- (1+2α)(2+α) = 2 + 2α + 2α2
Now using the formula above for α2
- (1+2α)(2+α)
- = 2 + 2α + 2(2α+1)
- = 2 + 2α+4α+2
- = 2 + 6α+2
- = 2 + 2 = 4 = 1
Verify for yourself that multiplication and other operations work too.
Primitive elements
editRecall from Modular arithmetic that the order of a number a modulo n, in a field, is the least power such that ak-1=1 in Zn, with k the size of this field. Since the order is defined over a field, this leads us to consider whether we have primitive elements in F[x]/<m(x)> - which we do. If we have F(α), just like in Zn, α is primitive iff the order of α is q-1 where q is the number of elements in F[x]/<m(x)>.
Let's take Z2/<x2+x+1>. Is α (root of x2+x+1) primitive?
First, if α is a root of x2+x+1,
- α2+α+1=0
- α2=-α-1=α+1
Now, let us calculate powers of α
- 1, α
- α2=α+1
- α3=α(α2)=α(α+1)=α2+α=(α+1)+α=1
Recall that the size of this field is 4 (the n in Zn, in this case, 2, raised to the power of the degree of the polynomial, in this case 2). Now we have α3=α4-1=1, and α is primitive.
We generally want to look at powers of α in F(α), to see whether they are primitive, since we already know about the orders of the constants in F(α) - which we've looked at in Modular arithmetic.
Arithmetic Functions
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
An arithmetic function[1] is a function from the set of positive integers to the set of complex numbers. Examples of important arithmetic functions include:
Euler totient function
editThe Euler totient function, defined to be the number of positive integers less than and relatively prime to n
Mobius function
editThe Mobius function,
Von Mangoldt function
editThe Von Mangoldt function,
and
Many of these functions are multiplicative that is they satisfy a(m)a(n)=a(mn) when m and n are relatively prime. A function that satisfies a(m)a(n)=a(mn) even when m & n are not relatively prime is called completely multiplicative. To define a multiplicative function, a(n), it suffices to only give its values when n is the power of a prime; For a completely multiplicative function, giving its values when n is prime uniquely defines the function.
Given 2 arithmetic functions their Dirichlet convolution is defined by
where the sum is taken over the divisors, d, of n. It is easy to show that
,
that is the function e(n) is the identity under Dirichlet convolution. Another basic fact is that Dirichlet convolution is commutative and associative.
It is also straightfoward to show that multiplicative functions form a group under Dirichlet convolution, or in other words, the following properties hold in addition to the fact that e(n) is the identity, and its associativity:
- for any multiplicative function a there is a multiplicative function b such that (a * b) = e
and
- the Dirichlet convolution of 2 multiplicative functions is also multiplicative.
The most important fact about the Von Mangoldt function is that
.
The Mobius function's significance comes from the fact that
,
and thus if then .
References
editAnalytic Number Theory
editIntroduction
editAnalytic Number Theory is the application of Analysis to Number Theoretic Problems. A quick overview of some portions of Analytic Number theory follow.
Zeta function
editThe zeta function, defined by
for real values of s > 1, plays a central role in the theory. It converges absolutely when s > 1. It satisfies the Euler product formula,
where the product is over all prime numbers. To see this, note that multiplying the series definition by 1-2-s and rearranging terms(which is justified since the series converges absolutely) eliminates the even terms, i.e.
Likewise after multiplying by 1-3-s all remaining terms with n divisible by 3 are eliminated. After repeating this process for all primes it follows that
since 1 is the only number not divisible by a prime and thus only the n=1 term is left. Solving for ζ(s) immediately gives the Euler product formula.
Dirichlet series
editThe series for the zeta function is a special case of a Dirichlet series. A Dirichlet series is one of the form
where is a sequence of complex numbers.
Many important arithmetic functions, , have the properties that and when and are relatively prime. Such functions are called multiplicative.
For a multiplicative function , its associated Dirichlet series may be expressed as an Euler product by
.
This can be shown in a manner similar to the proof for the zeta function.
A completely multiplicative function is one where even if and are not relatively prime.
For a completely multiplicative function, the Euler product simplifies to
.
The product of two Dirichlet series is given by the formula
where represents the Dirichlet convolution of and , which is defined by
Some important Dirichlet series include:
and
Big-Oh notation
editMany problems involve functions that are incredibly difficult to work with exactly, but where the rate of growth of the function, rather than its exact values, is of primary concern. Because of this a notation (often called "Big-Oh notation") was invented.
The notation
is used to denote that, for a sufficiently large number , there exists a number such that
for all .
The expression denotes that .
Dirichlet's Theorem
editOne of the first results proven with analytic number theory was Dirichlet's Theorem which states that for any 2 relatively prime integers a & b, there are infinitely many values of k for which ak+b is a prime number. The proof involves complex-valued functions of the set of integers called Dirichlet characters defined by the properties that χ(n) depends only on its residue class modulo a, χ(n) is completely multiplicative, and χ(n) = 0 iff a and n are not relatively prime. The principal character χ0 is defined to be 1 when a & n are relatively prime and 0 otherwise. It is easy to show that χ0 is a character. It can be shown that the number of characters is equal to φ(a). It can also be shown that the sum of the values of χ(n) over all characters χ is equal to φ(a) if and 0 otherwise. The Dirichlet series corresponding to a character is called a Dirichlet L-series and is traditionally denoted by L(s,χ). It is simple to show that L(1,χ0) diverges. Through a complicated argument it is shown that L(1,χ) converges and is nonzero if χ is nonprincipal. The function
must diverge since L(1,χ0)/χ(b) diverges and the other terms all converge. Since all terms of the sum on the left are finite its divergence implies there are an infinite number of terms of this sum and thus infinitely many primes of the form ak+b.
Riemann zeta function & xi function
editThe zeta function introduced above(the Euler zeta function) converges for all values of s such that Re(s)>1. The Riemann zeta function is defined as the analytic continuation of the Euler zeta function, and is defined for all complex values of s except s=1. Where both functions exist, the Euler and Riemann zeta functions are equal by definition. It can be shown that if the xi function is defined by
then ξ(s)=ξ(1-s). This is the symmetric form of the famous functional equation for the Riemann zeta function, and provides a convenient way of computing the Riemann zeta function when Re(s)<1.
The series definition of Euler's zeta function shows that ζ(s) has no zeroes for Re(s)>1. It can also be shown that the zeta function has no zeroes with Re(s)=1. The functional equation shows that for integer values of n, ζ(-2n)=0, and any other zeroes lie in the so-called critical strip, 0<Re(s)<1. The well-known Riemann Hypothesis states that all nontrivial zeros(i.e. those not of the form s=-2n), have Re(s)=1/2. It is easy to show that the zeroes of the xi function are exactly the nontrivial zeroes of the zeta function.
Hadamard product formula
editThe Hadamard product formula states that functions with certain properties(in particular the xi function) are close enough to a polynomial that they may be represented in terms of a product over the zeroes. For the xi function the Hadamard product formula states that
for certain values of A and B, where the product is over the zeroes of ξ(s). This formula is one of the main reasons the zeroes of the xi function, and thus the zeta function, are of considerable importance.
Distribution of squarefree numbers
editLet S(x) denote the number of squarefree numbers less than or equal to x. To evaluate this function we begin by counting all integers less than or equal to x. Then we subtract those that are divisible by 4, those divisible by 9, those divisible by 25, and so on. We then have removed numbers with 2 repeated prime factors twice those with 3 repeated prime factors 3 times and so on. To remedy the repetition of the numbers with 2 repeated prime factors we add on the number of integers less than or equal to x divisible by 36, those divisible by 100, those divisible by 225 and so on. We have now reincluded those with 3 repeated prime factors so we uncount them. Continuing this process gives
In addition to information about how common squarefree numbers are this estimate gives information on how they are distributed. For example to show that there are infinitely many pairs of consecutive squarefree numbers(i.e. that differ by 1) assume there are only finitely many such pairs. Then there is some x0 such that all such pairs lie below x0. Then for n > x0 n and n+1 cannot be squarefree, and thus at most half the integers above x0 are squarefree, or more precisely,
but since this contradicts the estimate obtained earlier, thus there are infinitely many pairs of consecutive squarefree numbers.
The estimate also shows that for large enough x, there is at least one squarefree number between x^3 and (x+1)^3. To see this, note that the number of squarefree numbers in that range is
which is at least one for sufficiently large x.
To do: Add mention of prime number theorem and sieve methods, as well as Dirichlet inversion
Upper-level logic
editGodel's incompleteness theorem
editThere's no mathematical system with consistent axiom.
Second order logic
editDiscrete Mathematics/Second order logic
Upper-level Combinatorics
editAutomata
editFinite state automata
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
Formally, a Deterministc Finite Automaton (DFA) is a 5-tuple where:
- Q is the set of all states.
- is the alphabet being considered.
- is the set of transitions, including exactly one transition per element of the alphabet per state.
- is the single starting state.
- F is the set of all accepting states.
For a DFA, can be viewed as a function from .
Example: Consider the DFA with transitions given by table:
| a | b | |
|---|---|---|
| p | q | p |
| q | p | q |
It is easy to verify that this DFA accepts the input "aaa".
Similarly, the formal definition of a Nondeterministic Finite Automaton is a 5-tuple where:
- Q is the set of all states.
- is the alphabet being considered.
- is the set of transitions, with transitions and any number of transitions for any particular input on every state.
- is the single starting state.
- F is the set of all accepting states.
For a NFA, can be viewed as a function from where is the power set of .
Note that for both a NFA and a DFA, is not a set of states. Rather, it is a single state, as neither can begin at more than one state. However, a NFA can achieve similar function by adding a new starting state and epsilon-transitioning to all desired starting states.
The difference between a DFA and an NFA being the delta-transitions are allowed to contain epsilon-jumps(transitions on no input), unions of transitions on the same input, and no transition for any elements in the alphabet.
For any NFA , there exists a DFA such that
Pushdown automata
editDiscrete Mathematics/Pushdown automata
Turing machines
editDiscrete Mathematics/Turing machines
Cellular automata
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
A cellular automaton is a collection of "colored" cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules based on the states of neighboring cells. The rules are then applied iteratively for as many time steps as desired
Further problems
editSelected problems
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
The problems in the texts you have seen are for you to ensure that you understand the concepts and ideas explored. They are not intended to be very difficult, but understandably they are not very challenging.
Questions here are intended for you to further use the ideas you have learnt to answer some more difficult questions. Some questions are relatively straightforward, some of these questions depend on different sections of this discrete mathematics text, some of these questions are meant to be examination-style questions.
Do not be discouraged by the increase in difficulty - hints are sometimes available, and you will be able to increase your problem solving skills!
Set theory questions
editThese questions depend on your knowledge of Set theory.
- We have the sets A={0, 1, 3, 4, 5, 7}, B = {2, 4, 5, 8, 9}, C = {1, 4, 9, 11, 21}. Write the elements of the set Check your solution: [1]
- Using the set identities, simplify
- (Hint provided) Prove the set is not a subset of
- (Hint provided) Prove the set is not a subset of
Unordered pages
editCombinatory logic
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
Two of the basic principles of combinatory logic in discrete mathematics are the Sum principle and the Multiplication principle.
The sum principle holds true in a given partitioned set X where partition Xi intersected with Xj is the empty set unless i is equal to j. The principle states that in such a partitioned set, the sum of the elements of each partition is equal to the number of elements in the set X.
Languages and grammars
editDiscrete Mathematics/Languages and grammars
Axiom of choice
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |
Axiom of choice:
If is a surjective map, then there exists a map such that is the identity (trivial) map.
Lemma: Every set can be well-ordered.
Naive set theory
editWhen we talk of set theory, we generally talk about collections of certain mathematical objects. In this sense, a set can be likened to a bag, holding a finite (or conceivably infinite) amount of things. Sets can be sets of sets as well (bags with bags in them). However, a set cannot contain duplicates -- a set can contain only one copy of a particular item.
When we look at sets of certain types of numbers, for example, the natural numbers, or the rational numbers, for instance, we may want to speak only of these sets. These collections of numbers are, of course, very important, so we write special symbols to signify them.
We write sets in curly brackets -- { and }. We write all of the elements, or what the set contains, in the brackets, separated by commas. We generally denote sets using capital letters.
For example, we write the set containing the number 0 and the number 1 as {0,1}. If we wish to give it a name, we can say B={0,1}.
Special sets
editThe aforementioned collections of numbers, the naturals, rationals, etc. are notated as the following:
- the natural numbers are written
- {0,1,2,...}
- the integers are written
- {0,1,-1,2,-2,...}
- the rational numbers are written
- {0,1,1/2,1/3,...,2,2/3,2/4,...}
- the real numbers are written
- {0,,,,...}
Here we will generally write these in standard face bold instead of the doublestruck bold you see above. So we write here N instead of (NB following Wikipedia conventions).
Notations
editWe can write some special relations involving sets using some symbols.
Containment relations
editTo say that an element is in a set, for example, 3 is in the set {1,2,3}, we write:
We can also express this relationship in another way: we say that 3 is a member of the set {1,2,3}. Also, we can say the set {1,2,3} contains 3, but this usage is not recommended as it is also used to refer to subsets (see following).
We can say that two sets are equal if they contain exactly the same elements. For example, the sets {2,3,1} and {3,1,2} both contain the numbers 1, 2 and 3. We write:
We write the set with no elements as , or {}. Here, we use the notation {} for the empty set (NB following Wikipedia conventions).
The concept of the subset
editA very important concept in set theory and other mathematical areas is the concept of the subset.
Say we have two sets A={0,1,2,3,4,5,6,7,8,9}, and B={0,1,2,3,4,5}. Now, B contains some elements of A, but not all. We express this relationship between the sets A and B by saying B is a subset of A. We write this
If B is a subset of A, but A is not a subset of B, B is said to be a proper subset of A. We write this
Note that if , then
Intersections and unions
editThere are two notable and fundamental special operations on sets, the intersection and the union. These are somewhat analogous to multiplication and addition.
Intersection
editThe intersection of two sets A and B are the elements common to both sets. For example, if A={1,3,5,7,9} and B={0,1,3}, their intersection, written is the set {1,3}.
If the intersection of any two sets are empty, we say these sets are disjoint.
Unions
editThe union of two sets A and B are the all elements in both sets. For example if A={1,3,5,7,9} and B={0,2,4,6,8}. We say the union, written is the set {0,1,2,3,4,5,6,7,8,9}.
Set comprehensions
editWhen we write a set, we can do so by writing all the elements in that set as above. However if we wish to write an infinite set, then writing out the elements can be too unwieldy. We can solve this problem by writing sets in set comprehension notation. We do this by writing these sets including a rule and by a relationship to an index set, say I. That is;
where rule can be something like x2, or x=3x.
For example, this set forms the set of all even numbers:
This set forms the set of all solutions to the general quadratic:
Universal sets and complements
editUniversal sets
editWhen we do work with sets, it is useful to think of a larger set in which to work with. For example, if we are talking about sets {-1,0,1} and {-3,-1,1,3}, we may want to work in Z in this circumstance. When we talk about working in such a larger set, such as Z in that instance, we say that Z is a universal set, and we take all sets to be subsets of this universal set.
We write the universal set to be , however it may be simpler to denote this as E.
Complements
editGiven a set A in a larger universal set E, we define the complement of A to be all elements in E that are not in A, that is the complement of A is:
We write the complement as A' or Ac. In this document we will use A'.
Problem set
editBased on the above information, write the answers to the following questions (Answers follow to even numbered questions)
- Is ?
- Is ?
- Is ?
- True or false? If false, give an example of an element in the first set which is not in the second.
- True or false? If false, give an example of an element in the first set which is not in the second.
- Is ?
- Is ?
- Write the 5 elements of
- Write the elements of
- Find a universal set such that these sets are subsets thereof:
- Given , find A' given
Answers
edit2. No, the square root of 2 is irrational, not a rational number
4.1. Yes
4.2. No
6. Yes.
8. 5 elements could be {3,5,7,9,11}.
10.
Further ideas
editThese mentioned concepts are not the only ones we can give to set theory. Key ideas that are not necessarily given much detail in this elementary course in set theory but later in abstract algebra and other fields, so it is important to take a grasp on these ideas now.
These may be skipped.
Power set
editThe power set, denoted P(S), is the set of all subsets of S. NB: The empty set is a subset of all sets.
For example, P({0,1})={{},{0},{1},{0,1}}
Cardinality
editThe cardinality of a set, denoted |S| is the amount of elements a set has. So |{a,b,c,d}|=4, and so on. The cardinality of a set need not be finite: some sets have infinite cardinality.
The cardinality of the power set
editIf P(S)=T, then |T|=2|S|.
Problem set
editBased on the above information, write the answers to the following questions. (Answers follow to even numbered questions)
- |{1,2,3,4,5,6,7,8,9,0}|
- |P({1,2,3})|
- P({0,1,2})
- P({1})
Answers
edit2. 23=8
4. {{},{1}}
Set identities
editWhen we spoke of the two fundamental operators on sets before, that of the union and the intersection, we have a set of rules which we can use to simplify expressions involving sets. For example, given:
how can we simplify this?
Several of the following set identities are similar to those in standard mathematics
This is incomplete and a draft, additional information is to be added
Sieve of Eratosthenes
edit| This page or section is an undeveloped draft or outline. You can help to develop the work, or you can ask for assistance in the project room. |

The Sieve of Eratosthenes is a method for find prime numbers that is attributed to the ancient Greek mathematician Eratosthenes. The idea is to begin by listing all the natural numbers bigger than 2.
and beginning with 2 we go to the first number that has not been crossed off and cross every multiple of that number that is later on in the list.
So in the case of 2, no numbers have been crossed so we start by removing every second number after 2. Our list would then look like
And we keep applying our rule. Here our next number not crossed out will be 3, we cross out every third number after 3. That will be 6, 9, 12,… and our list the becomes
And so on. At the end only the prime numbers will be left.
In this case we have already found all of the primes less than 25. This is because composite numbers must always have a prime factor less than their square root. If this were not the case for some integer we could write . Since we are assuming is composite we know there are at least two prime factors and . If both of which are greater than , then . This would contradict that . So for us, since we have crossed out every number with a factor smaller than 5 we have crossed out every composite number less than .




































































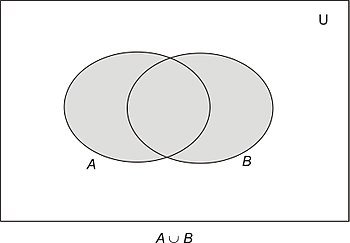























































































































































![{\displaystyle S_{\infty }([x_{1},x_{2}]\times [y_{1},y_{2}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fdf6a1036e157c05e81566820f28f64cef15896)




![{\displaystyle S_{\infty }([x,x]\times [y,y+(n-1)])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11fc6af0cd65bfd631106e6452272527e32f9928)


![{\displaystyle S_{\infty }([x,x+(m-1)]\times [y,y+(n-1)])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e872a6ce51605ba520f6fd055f358cdf20c6786c)































![{\displaystyle S_{1}[x_{1},x_{2}];S_{2}[x_{1},x_{2}];S_{1,2}[x_{1},x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24ad46732aa1fd647ad7eac65c266c86b84bebdf)


![{\displaystyle ...,S_{1,2}[-2m_{1},-m_{1}-1],S_{1,2}[-m_{1},-1],S_{1,2}[0,m_{1}-1],S_{1,2}[m_{1},2m_{1}-1],S_{1,2}[2m_{1},3m_{1}-1],...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03066ba7100d2cc10b9db488dd02e1d870f278b0)

![{\displaystyle S_{1,2}[km_{1},(k+1)m_{1}-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a71049057141c958da783478dc2d1d6abc44a2a)








![{\displaystyle S_{1,2}[km_{1},(k+1)m_{1}-1]=S_{1,2}[(k+p)m_{1},(k+p+1)m_{1}-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d148d8c7b797279a4afc023a1eff2c281814b28)



































































![{\displaystyle \forall x\forall y[\forall z(z\in x\Leftrightarrow z\in y)\Rightarrow x=y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d7b175ec36a59df864706ac6cfa8976c10e71d0)
![{\displaystyle \forall x\forall y[\forall z(z\in x\Leftrightarrow z\in y)\Rightarrow \forall z(x\in z\Leftrightarrow y\in z)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44b1e8b20e39514ecabe08db08307aeb674e9878)
![{\displaystyle \forall x[\exists y(y\in x)\Rightarrow \exists y(y\in x\land \lnot \exists z(z\in y\land z\in x))].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ec56857b648d8db5fc0f7d01e19232afcc2ca15)

![{\displaystyle \forall z\forall w_{1}\ldots w_{n}\exists y\forall x[x\in y\Leftrightarrow (x\in z\land \phi )].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1f3d48564579cde9c898f3da6735629be01988)










![{\displaystyle \exists X\left[\varnothing \in X\land \forall y(y\in X\Rightarrow S(y)\in X)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd396541416f002cb2d9c916604004b292815d41)


![{\displaystyle \forall x\exists y\forall z[z\subseteq x\Rightarrow z\in y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f6acd98b5529aadefd8f2990b7b9c913d39f0ec)














![{\displaystyle [q_{0};q_{1},q_{2},q_{3},\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/725943b94feb7e4b2f8a53a218a97b9eeea41ab6)
![{\displaystyle \alpha =[3;1,2,5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3e358a4f19a575d936fe340de5e1e3fc1d48f4d)









![{\displaystyle {\begin{matrix}\alpha &=&[2;2,1,2,2,1...]\\&=&[2;{\overline {2,1,2}}]\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6ffda5585980cf382228697c71c7b93b517a20a)
![{\displaystyle [2;{\overline {2,1,2}}]=[2;2,1,{\overline {2,2,1}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2bf93e79f3e264892c6d0802d1b5cec4bf8aaab)


























![{\displaystyle \mathbf {F} [x]/\langle m(x)\rangle =\{a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots +a_{0}x^{0}|a_{i}\in \mathbf {F} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98409b3439490039211fd4c2ae55bab432d6ac29)
![{\displaystyle |\mathbf {F} [x]/\langle m(x)\rangle |=p^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ca63e276010649c974002e05254013737354e85)







































































































