A-level Physics (Advancing Physics)/Transformers
We have already seen that a change in flux induces an emf in a coil, given by Faraday's Law:
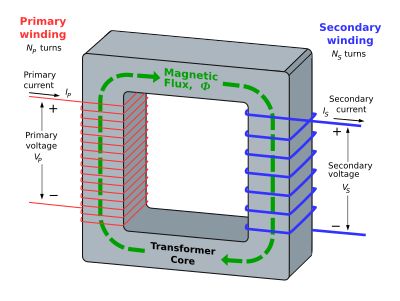
We have also seen that a current in a coil induces a magnetic flux inside the coil. If we were to connect two coils with the same core, the flux, and the rate of change of flux, would be exactly the same inside both coils. We would have created a kind of flux circuit known as a transformer. The ratio between the voltage at the primary coil Vp and the voltage at the secondary coil Vs would have to be (since φ is the same for both transformers):
,
where Np and Ns are the numbers of coils in the primary and secondary coils respectively.
In other words, we can change the voltage of some electricity by varying the number of coils in each coil. In order for this to work, the current used must be an alternating current (AC). This means that the current and voltage are constantly changing sinusoidally, and so there is a sinusoidal change in flux. This means that an emf is induced in the secondary coil. If the flux did not change (i.e. we were using direct current), then no emf would be induced, and the transformer would be useless except as a magnet (since it would still have a flux circuit in it).
Ideal Transformers
editAn ideal transformer is one in which all the electrical energy put into one coil comes out of the other coil. An ideal transformer does not exist, but, since it makes the maths easy, we like to pretend that it does. In this case, the power in must equal the power out:
,
where Ip and Is are the currents in the primary and secondary coils, respectively. So:
and
By substitution into the transformer equation for voltage:
So, in an ideal transformer, the ratio between the voltages is equal to the ratio between the numbers of coils, but the ratio between the currents is equal to the reciprocal of the ratio between the numbers of coils.
Eddy Currents
editIn reality, the electrical energy is not all conserved - a lot of it is converted into heat by eddy currents. In a transformer, the magnetic flux created by the primary coil induces a current in the core. This occurs in order to oppose the charge that produced the magnetic flux (Lenz's Law). The currents flowing in the core are called eddy currents.
These currents produce heat, using up energy and so causing inefficiency. One way of minimising the effects of eddy currents is to make the core out of iron laminate. This is layers of iron separated by thin layers of an insulator such as varnish. The amplitude of the eddy currents produced is reduced as currents cannot flow through the layers of insulator. (Note: OCR B question papers tend to have a question on eddy currents)
Questions
edit1. A step-down transformer has 300 coils on one coil, and 50 coils on the other. If 30 kV AC is put in, what voltage comes out?
2. A step-up transformer has 200 coils on one coil, and 980 coils on the other. If 25 kV AC comes out, what voltage was put in?
3. An ideal transformer transforms a 50A current into a 1A current. It has 40 coils on the primary coil. How many coils are in the secondary coil?
4. Transformers tend to vibrate. Why is this? What effect does this have on the efficiency of the transformer?
5. Air does have some permeability. What effect does this have on the efficiency of the transformer? Why?

