A-level Physics (Advancing Physics)/Phasors
Consider the image on the right. It shows a wave travelling through a medium. The moving blue dot represents the displacement caused to the medium by the wave. It can be seen that, if we consider any one point in the medium, it goes through a repeating pattern, moving up and down, moving faster the nearer it is to the centre of the waveform. Its height is determined by the amplitude of the wave at that point in time. This is determined by a sine wave.
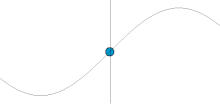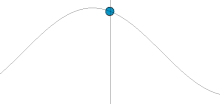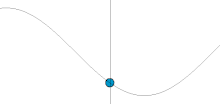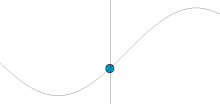

Phasors are a method of describing waves which show two things: the displacement caused to the medium, and the point in the repeating waveform which is being represented. They consist of a circle. An arrow moves round the circle anticlockwise as the wave pattern passes. For every wavelength that goes past, the arrow moves 360°, or 2πc, starting from the right, as in trigonometry. The angle of the arrow from the right is known as the phase angle, and is usually denoted θ, and the radius of the circle is usually denoted a. The height of the point at the end of the arrow represents the displacement caused by the wave to the medium, and so the amplitude of the wave at that point in time. The time taken to rotate 360° is known as the periodic time, and is usually denoted T.
Phase difference is the difference between the angles (θ) of two phasors, which represent two waves. It is never more than 180°, as, since the phasor is moving in a circle, the angle between two lines touching the circumference will always be less than or equal to 180°. It can also be expressed in terms of λ, where λ is the total wavelength (effectively, 360°). You can use trigonometry to calculate the displacement from the angle, and vice-versa, provided you know the radius of the circle. The radius is equal to the maximum amplitude of the wave.
Phasors can be added up, just like vectors: tip-to-tail. So, for example, when two waves are superposed on each other, the phasors at each point in the reference material can be added up to give a new displacement. This explains both constructive and destructive interference as well. In destructive interference, the phasors for each wave are pointing in exactly opposite directions, and so add up to nothing at all. In constructive interference, the phasors are pointing in the same direction, so the total displacement is twice as much.
Questions
edit1. A sine wave with wavelength 0.1m travels through a given point on the surface of the sea. A phasor arrow representing the effect of this wave on this point rotates 1000°. How many wavelengths have gone past in the time taken for the phasor to rotate this much?
2. A sine wave has a maximum amplitude of 500 nm. What is its amplitude when the phasor has rotated 60° from its start position?
3. Two waves have a phase difference of 45°. When the first wave is at its minimum amplitude of -0.3m, what is the total amplitude of the superposed waveforms?