This Quantum World/print version
| This is the print version of This Quantum World You won't see this message or any elements not part of the book's content when you print or preview this page. |
The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
//en.wikibooks.org/wiki/This_Quantum_World
Atoms
editWhat does an atom look like?
editLike this?
editOr like this?
editNone of these images depicts an atom as it is. This is because it is impossible to even visualize an atom as it is. Whereas the best you can do with the images in the first row is to erase them from your memory—they represent a way of viewing the atom that is too simplified for the way we want to start thinking about it—the eight fuzzy images in the next row deserve scrutiny. Each represents an aspect of a stationary state of atomic hydrogen. You perceive neither the nucleus (a proton) nor the electron. What you see is a fuzzy position. To be precise, what you see are cloud-like blurs, which are symmetrical about the vertical and horizontal axes, and which represent the atom's internal relative position—the position of the electron relative to the proton or the position of the proton relative to the electron.
- What is the state of an atom?
- What is a stationary state?
- What exactly is a fuzzy position?
- How does such a blur represent the atom's internal relative position?
- Why can we not describe the atom's internal relative position as it is?
Quantum states
editIn quantum mechanics, states are probability algorithms. We use them to calculate the probabilities of the possible outcomes of measurements on the basis of actual measurement outcomes. A quantum state takes as its input
- one or several measurement outcomes,
- a measurement M,
- the time of M,
and it yields as its output the probabilities of the possible outcomes of M.
A quantum state is called stationary if the probabilities it assigns are independent of the time of the measurement.
From the mathematical point of view, each blur represents a density function . Imagine a small region like the little box inside the first blur. And suppose that this is a region of the (mathematical) space of positions relative to the proton. If you integrate over you obtain the probability of finding the electron in provided that the appropriate measurement is made:
"Appropriate" here means capable of ascertaining the truth value of the proposition "the electron is in ", the possible truth values being "true" or "false". What we see in each of the following images is a surface of constant probability density.
Now imagine that the appropriate measurement is made. Before the measurement, the electron is neither inside nor outside . If it were inside, the probability of finding it outside would be zero, and if it were outside, the probability of finding it inside would be zero. After the measurement, on the other hand, the electron is either inside or outside
Conclusions:
- Before the measurement, the proposition "the electron is in " is neither true nor false; it lacks a (definite) truth value.
- A measurement generally changes the state of the system on which it is performed.
As mentioned before, probabilities are assigned not only to measurement outcomes but also on the basis of measurement outcomes. Each density function serves to assign probabilities to the possible outcomes of a measurement of the electron's position relative to the proton. And in each case the assignment is based on the outcomes of a simultaneous measurement of three observables: the atom's energy (specified by the value of the principal quantum number ), its total angular momentum (specified by a letter, here p, d, or f), and the vertical component of its angular momentum .
Fuzzy observables
editWe say that an observable with a finite or countable number of possible values is fuzzy (or that it has a fuzzy value) if and only if at least one of the propositions "The value of is " lacks a truth value. This is equivalent to the following necessary and sufficient condition: the probability assigned to at least one of the values is neither 0 nor 1.
What about observables that are generally described as continuous, like a position?
The description of an observable as "continuous" is potentially misleading. For one thing, we cannot separate an observable and its possible values from a measurement and its possible outcomes, and a measurement with an uncountable set of possible outcomes is not even in principle possible. For another, there is not a single observable called "position". Different partitions of space define different position measurements with different sets of possible outcomes.
- Corollary: The possible outcomes of a position measurement (or the possible values of a position observable) are defined by a partition of space. They make up a finite or countable set of regions of space. An exact position is therefore neither a possible measurement outcome nor a possible value of a position observable.
So how do those cloud-like blurs represent the electron's fuzzy position relative to the proton? Strictly speaking, they graphically represent probability densities in the mathematical space of exact relative positions, rather than fuzzy positions. It is these probability densities that represent fuzzy positions by allowing us to calculate the probability of every possible value of every position observable.
It should now be clear why we cannot describe the atom's internal relative position as it is. To describe a fuzzy observable is to assign probabilities to the possible outcomes of a measurement. But a description that rests on the assumption that a measurement is made, does not describe an observable as it is (by itself, regardless of measurements).
Planck
editQuantum mechanics began as a desperate measure to get around some spectacular failures of what subsequently came to be known as classical physics.
In 1900 Max Planck discovered a law that perfectly describes the spectrum of a glowing hot object. Planck's radiation formula turned out to be irreconcilable with the physics of his time. (If classical physics were right, you would be blinded by ultraviolet light if you looked at the burner of a stove, aka the UV catastrophe.) At first, it was just a fit to the data, "a fortuitous guess at an interpolation formula" as Planck himself called it. Only weeks later did it turn out to imply the quantization of energy for the emission of electromagnetic radiation: the energy of a quantum of radiation is proportional to the frequency of the radiation, the constant of proportionality being Planck's constant
- .
We can of course use the angular frequency instead of . Introducing the reduced Planck constant , we then have
- .
This theory is valid at all temperatures and helpful in explaining radiation by black bodies.
Rutherford
editIn 1911 Ernest Rutherford proposed a model of the atom based on experiments by Geiger and Marsden. Geiger and Marsden had directed a beam of alpha particles at a thin gold foil. Most of the particles passed the foil more or less as expected, but about one in 8000 bounced back as if it had encountered a much heavier object. In Rutherford's own words this was as incredible as if you fired a 15 inch cannon ball at a piece of tissue paper and it came back and hit you. After analysing the data collected by Geiger and Marsden, Rutherford concluded that the diameter of the atomic nucleus (which contains over 99.9% of the atom's mass) was less than 0.01% of the diameter of the entire atom. He suggested that the atom is spherical in shape and the atomic electrons orbit the nucleus much like planets orbit a star. He calculated mass of electron as 1/7000th part of the mass of an alpha particle. Rutherford's atomic model is also called the Nuclear model.
The problem of having electrons orbit the nucleus the same way that a planet orbits a star is that classical electromagnetic theory demands that an orbiting electron will radiate away its energy and spiral into the nucleus in about 0.5×10-10 seconds. This was the worst quantitative failure in the history of physics, under-predicting the lifetime of hydrogen by at least forty orders of magnitude! (This figure is based on the experimentally established lower bound on the proton's lifetime.)
Bohr
editIn 1913 Niels Bohr postulated that the angular momentum of an orbiting atomic electron was quantized: its "allowed" values are integral multiples of :
- where
Why quantize angular momentum, rather than any other quantity?
- Radiation energy of a given frequency is quantized in multiples of Planck's constant.
- Planck's constant is measured in the same units as angular momentum.
Bohr's postulate explained not only the stability of atoms but also why the emission and absorption of electromagnetic radiation by atoms is discrete. In addition it enabled him to calculate with remarkable accuracy the spectrum of atomic hydrogen — the frequencies at which it is able to emit and absorb light (visible as well as infrared and ultraviolet). The following image shows the visible emission spectrum of atomic hydrogen, which contains four lines of the Balmer series.

Apart from his quantization postulate, Bohr's reasoning at this point remained completely classical. Let's assume with Bohr that the electron's orbit is a circle of radius The speed of the electron is then given by and the magnitude of its acceleration by Eliminating yields In the cgs system of units, the magnitude of the Coulomb force is simply where is the magnitude of the charge of both the electron and the proton. Via Newton's the last two equations yield where is the electron's mass. If we take the proton to be at rest, we obtain for the electron's kinetic energy.
If the electron's potential energy at infinity is set to 0, then its potential energy at a distance from the proton is minus the work required to move it from to infinity,
The total energy of the electron thus is
We want to express this in terms of the electron's angular momentum Remembering that and hence and multiplying the numerator by and the denominator by we obtain
Now comes Bohr's break with classical physics: he simply replaced by . The "allowed" values for the angular momentum define a series of allowed values for the atom's energy:
As a result, the atom can emit or absorb energy only by amounts equal to the absolute values of the differences
one Rydberg (Ry) being equal to This is also the ionization energy of atomic hydrogen — the energy needed to completely remove the electron from the proton. Bohr's predicted value was found to be in excellent agreement with the measured value.
Using two of the above expressions for the atom's energy and solving for we obtain For the ground state this is the Bohr radius of the hydrogen atom, which equals The mature theory yields the same figure but interprets it as the most likely distance from the proton at which the electron would be found if its distance from the proton were measured.
de Broglie
editIn 1923, ten years after Bohr had derived the spectrum of atomic hydrogen by postulating the quantization of angular momentum, Louis de Broglie hit on an explanation of why the atom's angular momentum comes in multiples of Since 1905, Einstein had argued that electromagnetic radiation itself was quantized (and not merely its emission and absorption, as Planck held). If electromagnetic waves can behave like particles (now known as photons), de Broglie reasoned, why cannot electrons behave like waves?
Suppose that the electron in a hydrogen atom is a standing wave on what has so far been thought of as the electron's circular orbit. (The crests, troughs, and nodes of a standing wave are stationary.) For such a wave to exist on a circle, the circumference of the latter must be an integral multiple of the wavelength of the former:
Einstein had established not only that electromagnetic radiation of frequency comes in quanta of energy but also that these quanta carry a momentum Using this formula to eliminate from the condition one obtains But is just the angular momentum of a classical electron with an orbit of radius In this way de Broglie derived the condition that Bohr had simply postulated.
Schrödinger
editIf the electron is a standing wave, why should it be confined to a circle? After de Broglie's crucial insight that particles are waves of some sort, it took less than three years for the mature quantum theory to be found, not once, but twice. By Werner Heisenberg in 1925 and by Erwin Schrödinger in 1926. If we let the electron be a standing wave in three dimensions, we have all it takes to arrive at the Schrödinger equation, which is at the heart of the mature theory.
Let's keep to one spatial dimension. The simplest mathematical description of a wave of angular wavenumber and angular frequency (at any rate, if you are familiar with complex numbers) is the function
Let's express the phase in terms of the electron's energy and momentum
The partial derivatives with respect to and are
We also need the second partial derivative of with respect to :
We thus have
In non-relativistic classical physics the kinetic energy and the kinetic momentum of a free particle are related via the dispersion relation
This relation also holds in non-relativistic quantum physics. Later you will learn why.
In three spatial dimensions, is the magnitude of a vector . If the particle also has a potential energy and a potential momentum (in which case it is not free), and if and stand for the particle's total energy and total momentum, respectively, then the dispersion relation is
By the square of a vector we mean the dot (or scalar) product . Later you will learn why we represent possible influences on the motion of a particle by such fields as and
Returning to our fictitious world with only one spatial dimension, allowing for a potential energy , substituting the differential operators and for and in the resulting dispersion relation, and applying both sides of the resulting operator equation to we arrive at the one-dimensional (time-dependent) Schrödinger equation:
In three spatial dimensions and with both potential energy and potential momentum present, we proceed from the relation substituting for and for The differential operator is a vector whose components are the differential operators The result:
where is now a function of and This is the three-dimensional Schrödinger equation. In non-relativistic investigations (to which the Schrödinger equation is confined) the potential momentum can generally be ignored, which is why the Schrödinger equation is often given this form:
The free Schrödinger equation (without even the potential energy term) is satisfied by (in one dimension) or (in three dimensions) provided that equals which is to say: However, since we are dealing with a homogeneous linear differential equation — which tells us that solutions may be added and/or multiplied by an arbitrary constant to yield additional solutions — any function of the form
with solves the (one-dimensional) Schrödinger equation. If no integration boundaries are specified, then we integrate over the real line, i.e., the integral is defined as the limit The converse also holds: every solution is of this form. The factor in front of the integral is present for purely cosmetic reasons, as you will realize presently. is the Fourier transform of which means that
The Fourier transform of exists because the integral is finite. In the next section we will come to know the physical reason why this integral is finite.
So now we have a condition that every electron "wave function" must satisfy in order to satisfy the appropriate dispersion relation. If this (and hence the Schrödinger equation) contains either or both of the potentials and , then finding solutions can be tough. As a budding quantum mechanician, you will spend a considerable amount of time learning to solve the Schrödinger equation with various potentials.
Born
editIn the same year that Erwin Schrödinger published the equation that now bears his name, the nonrelativistic theory was completed by Max Born's insight that the Schrödinger wave function is actually nothing but a tool for calculating probabilities, and that the probability of detecting a particle "described by" in a region of space is given by the volume integral
— provided that the appropriate measurement is made, in this case a test for the particle's presence in . Since the probability of finding the particle somewhere (no matter where) has to be 1, only a square integrable function can "describe" a particle. This rules out which is not square integrable. In other words, no particle can have a momentum so sharp as to be given by times a wave vector , rather than by a genuine probability distribution over different momenta.
Given a probability density function , we can define the expected value
and the standard deviation
as well as higher moments of . By the same token,
and
Here is another expression for
To check that the two expressions are in fact equal, we plug into the latter expression:
Next we replace by and shuffle the integrals with the mathematical nonchalance that is common in physics:
The expression in square brackets is a representation of Dirac's delta distribution the defining characteristic of which is for any continuous function (In case you didn't notice, this proves what was to be proved.)
Heisenberg
editIn the same annus mirabilis of quantum mechanics, 1926, Werner Heisenberg proved the so-called "uncertainty" relation
Heisenberg spoke of Unschärfe, the literal translation of which is "fuzziness" rather than "uncertainty". Since the relation is a consequence of the fact that and are related to each other via a Fourier transformation, we leave the proof to the mathematicians. The fuzziness relation for position and momentum follows via . It says that the fuzziness of a position (as measured by ) and the fuzziness of the corresponding momentum (as measured by ) must be such that their product equals at least
The Feynman route to Schrödinger
editThe probabilities of the possible outcomes of measurements performed at a time are determined by the Schrödinger wave function . The wave function is determined via the Schrödinger equation by What determines ? Why, the outcome of a measurement performed at — what else? Actual measurement outcomes determine the probabilities of possible measurement outcomes.
Two rules
editIn this chapter we develop the quantum-mechanical probability algorithm from two fundamental rules. To begin with, two definitions:
- Alternatives are possible sequences of measurement outcomes.
- With each alternative is associated a complex number called amplitude.
Suppose that you want to calculate the probability of a possible outcome of a measurement given the actual outcome of an earlier measurement. Here is what you have to do:
- Choose any sequence of measurements that may be made in the meantime.
- Assign an amplitude to each alternative.
- Apply either of the following rules:
Rule A: If the intermediate measurements are made (or if it is possible to infer from other measurements what their outcomes would have been if they had been made), first square the absolute values of the amplitudes of the alternatives and then add the results.
- Rule B: If the intermediate measurements are not made (and if it is not possible to infer from other measurements what their outcomes would have been), first add the amplitudes of the alternatives and then square the absolute value of the result.
In subsequent sections we will explore the consequences of these rules for a variety of setups, and we will think about their origin — their raison d'être. Here we shall use Rule B to determine the interpretation of given Born's probabilistic interpretation of .
In the so-called "continuum normalization", the unphysical limit of a particle with a sharp momentum is associated with the wave function
Hence we may write
is the amplitude for the outcome of an infinitely precise momentum measurement. is the amplitude for the outcome of an infinitely precise position measurement performed (at time t) subsequent to an infinitely precise momentum measurement with outcome And is the amplitude for obtaining by an infinitely precise position measurement performed at time
The preceding equation therefore tells us that the amplitude for finding at is the product of
- the amplitude for the outcome and
- the amplitude for the outcome (at time ) subsequent to a momentum measurement with outcome
summed over all values of
Under the conditions stipulated by Rule A, we would have instead that the probability for finding at is the product of
- the probability for the outcome and
- the probability for the outcome (at time ) subsequent to a momentum measurement with outcome
summed over all values of
The latter is what we expect on the basis of standard probability theory. But if this holds under the conditions stipulated by Rule A, then the same holds with "amplitude" substituted from "probability" under the conditions stipulated by Rule B. Hence, given that and are amplitudes for obtaining the outcome in an infinitely precise position measurement, is the amplitude for obtaining the outcome in an infinitely precise momentum measurement.
Notes:
- Since Rule B stipulates that the momentum measurement is not actually made, we need not worry about the impossibility of making an infinitely precise momentum measurement.
- If we refer to as "the probability of obtaining the outcome " what we mean is that integrated over any interval or subset of the real line is the probability of finding our particle in this interval or subset.
An experiment with two slits
edit
In this experiment, the final measurement (to the possible outcomes of which probabilities are assigned) is the detection of an electron at the backdrop, by a detector situated at D (D being a particular value of x). The initial measurement outcome, on the basis of which probabilities are assigned, is the launch of an electron by an electron gun G. (Since we assume that G is the only source of free electrons, the detection of an electron behind the slit plate also indicates the launch of an electron in front of the slit plate.) The alternatives or possible intermediate outcomes are
- the electron went through the left slit (L),
- the electron went through the right slit (R).
The corresponding amplitudes are and
Here is what we need to know in order to calculate them:
- is the product of two complex numbers, for which we shall use the symbols and
- By the same token,
- The absolute value of is inverse proportional to the distance between A and B.
- The phase of is proportional to
For obvious reasons is known as a propagator.
Why product?
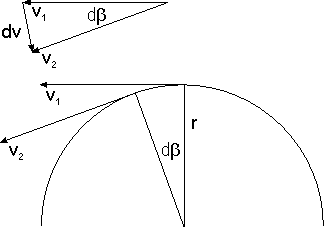
editRecall the fuzziness ("uncertainty") relation, which implies that as In this limit the particle's momentum is completely indefinite or, what comes to the same, has no value at all. As a consequence, the probability of finding a particle at B, given that it was last "seen" at A, depends on the initial position A but not on any initial momentum, inasmuch as there is none. Hence whatever the particle does after its detection at A is independent of what it did before then. In probability-theoretic terms this means that the particle's propagation from G to L and its propagation from L to D are independent events. So the probability of propagation from G to D via L is the product of the corresponding probabilities, and so the amplitude of propagation from G to D via L is the product of the corresponding amplitudes.
Why is the absolute value inverse proportional to the distance?
editImagine (i) a sphere of radius whose center is A and (ii) a detector monitoring a unit area of the surface of this sphere. Since the total surface area is proportional to and since for a free particle the probability of detection per unit area is constant over the entire surface (explain why!), the probability of detection per unit area is inverse proportional to The absolute value of the amplitude of detection per unit area, being the square root of the probability, is therefore inverse proportional to
Why is the phase proportional to the distance?
editThe multiplicativity of successive propagators implies the additivity of their phases. Together with the fact that, in the case of a free particle, the propagator (and hence its phase) can only depend on the distance between A and B, it implies the proportionality of the phase of to
Calculating the interference pattern
editAccording to Rule A, the probability of detecting at G an electron launched at D is
If the slits are equidistant from G, then and are equal and is proportional to
Here is the resulting plot of against the position of the detector:

(solid line) is the sum of two distributions (dotted lines), one for the electrons that went through L and one for the electrons that went through R.
According to Rule B, the probability of detecting at D an electron launched at G is proportional to
where is the difference and is the wavenumber, which is sufficiently sharp to be approximated by a number. (And it goes without saying that you should check this result.)
Here is the plot of against for a particular set of values for the wavenumber, the distance between the slits, and the distance between the slit plate and the backdrop:

Observe that near the minima the probability of detection is less if both slits are open than it is if one slit is shut. It is customary to say that destructive interference occurs at the minima and that constructive interference occurs at the maxima, but do not think of this as the description of a physical process. All we mean by "constructive interference" is that a probability calculated according to Rule B is greater than the same probability calculated according to Rule A, and all we mean by "destructive interference" is that a probability calculated according to Rule B is less than the same probability calculated according to Rule A.
Here is how an interference pattern builds up over time[1]:
-
100 electrons
-
3000 electrons
-
20000 electrons
-
70000 electrons
- ↑ A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, & H. Ezawa, "Demonstration of single-electron buildup of an interference pattern", American Journal of Physics 57, 117-120, 1989.
Bohm's story
editHidden Variables
editSuppose that the conditions stipulated by Rule B are met: there is nothing — no event, no state of affairs, anywhere, anytime — from which the slit taken by an electron can be inferred. Can it be true, in this case,
- that each electron goes through a single slit — either L or R — and
- that the behavior of an electron that goes through one slit does not depend on whether the other slit is open or shut?
To keep the language simple, we will say that an electron leaves a mark where it is detected at the backdrop. If each electron goes through a single slit, then the observed distribution of marks when both slits are open is the sum of two distributions, one from electrons that went through L and one from electrons that went through R:
If in addition the behavior of an electron that goes through one slit does not depend on whether the other slit is open or shut, then we can observe by keeping R shut, and we can observe by keeping L shut. What we observe if R is shut is the left dashed hump, and what we observed if L is shut is the right dashed hump:

Hence if the above two conditions (as well as those stipulated by Rule B) are satisfied, we will see the sum of these two humps. In reality what we see is this:

Thus all of those conditions cannot be simultaneously satisfied. If Rule B applies, then either it is false that each electron goes through a single slit or the behavior of an electron that goes through one slit does depend on whether the other slit is open or shut.
Which is it?
According to one attempt to make physical sense of the mathematical formalism of quantum mechanics, due to Louis de Broglie and David Bohm, each electron goes through a single slit, and the behavior of an electron that goes through one slit depends on whether the other slit is open or shut.
So how does the state of, say, the right slit (open or shut) affect the behavior of an electron that goes through the left slit? In both de Broglie's pilot wave theory and Bohmian mechanics, the electron is assumed to be a well-behaved particle in the sense that it follows a precise path — its position at any moment is given by three coordinates — and in addition there exists a wave that guides the electron by exerting on it a force. If only one slit is open, this passes through one slit. If both slits are open, this passes through both slits and interferes with itself (in the "classical" sense of interference). As a result, it guides the electrons along wiggly paths that cluster at the backdrop so as to produce the observed interference pattern:

According to this story, the reason why electrons coming from the same source or slit arrive in different places, is that they start out in slightly different directions and/or with slightly different speeds. If we had exact knowledge of their initial positions and momenta, we could make an exact prediction of each electron's subsequent motion. Obtaining this exact knowledge, however, is impossible in practice. The [[../../Serious illnesses/Born#Heisenberg|uncertainty principle ]] prevents us from making exact predictions of a particle's motion. Hence even though according to Bohm the initial positions and momenta are in possession of precise values, we can never know them.
If positions and momenta have precise values, then why can we not measure them? It used to be said that this is because a measurement exerts an uncontrollable influence on the value of the observable being measured. Yet this merely raises another question: why do measurements exert uncontrollable influences? This may be true for all practical purposes, but the uncertainty principle does not say that merely holds for all practical purposes. Moreover, it isn't the case that measurements necessarily "disturb" the systems on which they are performed.
The statistical element of quantum mechanics is an essential feature of the theory. The postulate of an underlying determinism, which in order to be consistent with the theory has to be a crypto-determinism, not only adds nothing to our understanding of the theory but also precludes any proper understanding of this essential feature of the theory. There is, in fact, a simple and obvious reason why hidden variables are hidden: the reason why they are strictly (rather than merely for all practical purposes) unobservable is that they do not exist.
At one time Einstein insisted that theories ought to be formulated without reference to unobservable quantities. When Heisenberg later mentioned to Einstein that this maxim had guided him in his discovery of the uncertainty principle, Einstein replied something to this effect: "Even if I once said so, it is nonsense." His point was that before one has a theory, one cannot know what is observable and what is not. Our situation here is different. We have a theory, and this tells in no uncertain terms what is observable and what is not.
Propagator for a free and stable particle
editThe propagator as a path integral
editSuppose that we make m intermediate position measurements at fixed intervals of duration Each of these measurements is made with the help of an array of detectors monitoring n mutually disjoint regions Under the conditions stipulated by Rule B, the propagator now equals the sum of amplitudes
It is not hard to see what happens in the double limit (which implies that ) and The multiple sum becomes an integral over continuous spacetime paths from A to B, and the amplitude becomes a complex-valued functional — a complex function of continuous functions representing continuous spacetime paths from A to B:
The integral is not your standard Riemann integral to which each infinitesimal interval makes a contribution proportional to the value that takes inside the interval, but a functional or path integral, to which each "bundle" of paths of infinitesimal width makes a contribution proportional to the value that takes inside the bundle.
As it stands, the path integral is just the idea of an idea. Appropriate evaluation methods have to be devised on a more or less case-by-case basis.
A free particle
editNow pick any path from A to B, and then pick any infinitesimal segment of . Label the start and end points of by inertial coordinates and respectively. In the general case, the amplitude will be a function of and In the case of a free particle, depends neither on the position of in spacetime (given by ) nor on the spacetime orientiaton of (given by the four-velocity but only on the proper time interval
(Because its norm equals the speed of light, the four-velocity depends on three rather than four independent parameters. Together with they contain the same information as the four independent numbers )
Thus for a free particle With this, the multiplicativity of successive propagators tells us that
It follows that there is a complex number such that where the line integral gives the time that passes on a clock as it travels from A to B via
A free and stable particle
editBy integrating (as a function of ) over the whole of space, we obtain the probability of finding that a particle launched at the spacetime point still exists at the time For a stable particle this probability equals 1:
If you contemplate this equation with a calm heart and an open mind, you will notice that if the complex number had a real part then the integral between the two equal signs would either blow up or drop off exponentially as a function of , due to the exponential factor .
Meaning of mass
editThe propagator for a free and stable particle thus has a single "degree of freedom": it depends solely on the value of If proper time is measured in seconds, then is measured in radians per second. We may think of with a proper-time parametrization of as a clock carried by a particle that travels from A to B via provided we keep in mind that we are thinking of an aspect of the mathematical formalism of quantum mechanics rather than an aspect of the real world.
It is customary
- to insert a minus (so the clock actually turns clockwise!):
- to multiply by (so that we may think of as the rate at which the clock "ticks" — the number of cycles it completes each second):
- to divide by Planck's constant (so that is measured in energy units and called the rest energy of the particle):
- and to multiply by (so that is measured in mass units and called the particle's rest mass):
The purpose of using the same letter everywhere is to emphasize that it denotes the same physical quantity, merely measured in different units. If we use natural units in which rather than conventional ones, the identity of the various 's is immediately obvious.
From quantum to classical
editAction
editLet's go back to the propagator
For a free and stable particle we found that
where is the proper-time interval associated with the path element . For the general case we found that the amplitude is a function of and or, equivalently, of the coordinates , the components of the 4-velocity, as well as . For a particle that is stable but not free, we obtain, by the same argument that led to the above amplitude,
where we have introduced the functional , which goes by the name action.
For a free and stable particle, is the proper time (or proper duration) multiplied by , and the infinitesimal action is proportional to :
Let's recap. We know all about the motion of a stable particle if we know how to calculate the probability (in all circumstances). We know this if we know the amplitude . We know the latter if we know the functional . And we know this functional if we know the infinitesimal action or (in all circumstances).
What do we know about ?
The multiplicativity of successive propagators implies the additivity of actions associated with neighboring infinitesimal path segments and . In other words,
implies
It follows that the differential is homogeneous (of degree 1) in the differentials :
This property of makes it possible to think of the action as a (particle-specific) length associated with , and of as defining a (particle-specific) spacetime geometry. By substituting for we get:
Something is wrong, isn't it? Since the right-hand side is now a finite quantity, we shouldn't use the symbol for the left-hand side. What we have actually found is that there is a function , which goes by the name Lagrange function, such that .
Geodesic equations
editConsider a spacetime path from to Let's change ("vary") it in such a way that every point of gets shifted by an infinitesimal amount to a corresponding point except the end points, which are held fixed: and at both and
If then
By the same token,
In general, the change will cause a corresponding change in the action: If the action does not change (that is, if it is stationary at ),
then is a geodesic of the geometry defined by (A function is stationary at those values of at which its value does not change if changes infinitesimally. By the same token we call a functional stationary if its value does not change if changes infinitesimally.)
To obtain a handier way to characterize geodesics, we begin by expanding
This gives us
Next we use the product rule for derivatives,
to replace the last two terms of (*), which takes us to
The second integral vanishes because it is equal to the difference between the values of the expression in brackets at the end points and where and If is a geodesic, then the first integral vanishes, too. In fact, in this case must hold for all possible (infinitesimal) variations and whence it follows that the integrand of the first integral vanishes. The bottom line is that the geodesics defined by satisfy the geodesic equations
Principle of least action
editIf an object travels from to it travels along all paths from to in the same sense in which an electron goes through both slits. Then how is it that a big thing (such as a planet, a tennis ball, or a mosquito) appears to move along a single well-defined path?
There are at least two reasons. One of them is that the bigger an object is, the harder it is to satisfy the conditions stipulated by Rule Another reason is that even if these conditions are satisfied, the likelihood of finding an object of mass where according to the laws of classical physics it should not be, decreases as increases.
To see this, we need to take account of the fact that it is strictly impossible to check whether an object that has travelled from to has done so along a mathematically precise path Let us make the half realistic assumption that what we can check is whether an object has travelled from to within a a narrow bundle of paths — the paths contained in a narrow tube The probability of finding that it has, is the absolute square of the path integral which sums over the paths contained in
Let us assume that there is exactly one path from to for which is stationary: its length does not change if we vary the path ever so slightly, no matter how. In other words, we assume that there is exactly one geodesic. Let's call it and let's assume it lies in
No matter how rapidly the phase changes under variation of a generic path it will be stationary at This means, loosely speaking, that a large number of paths near contribute to with almost equal phases. As a consequence, the magnitude of the sum of the corresponding phase factors is large.
If is not stationary at all depends on how rapidly it changes under variation of If it changes sufficiently rapidly, the phases associated with paths near are more or less equally distributed over the interval so that the corresponding phase factors add up to a complex number of comparatively small magnitude. In the limit the only significant contributions to come from paths in the infinitesimal neighborhood of
We have assumed that lies in If it does not, and if changes sufficiently rapidly, the phases associated with paths near any path in are more or less equally distributed over the interval so that in the limit there are no significant contributions to
For a free particle, as you will remember, From this we gather that the likelihood of finding a freely moving object where according to the laws of classical physics it should not be, decreases as its mass increases. Since for sufficiently massive objects the contributions to the action due to influences on their motion are small compared to this is equally true of objects that are not moving freely.
What, then, are the laws of classical physics?
They are what the laws of quantum physics degenerate into in the limit In this limit, as you will gather from the above, the probability of finding that a particle has traveled within a tube (however narrow) containing a geodesic, is 1, and the probability of finding that a particle has traveled within a tube (however wide) not containing a geodesic, is 0. Thus we may state the laws of classical physics (for a single "point mass", to begin with) by saying that it follows a geodesic of the geometry defined by
This is readily generalized. The propagator for a system with degrees of freedom — such as an -particle system with degrees of freedom — is
where and are the system's respective configurations at the initial time and the final time and the integral sums over all paths in the system's -dimensional configuration spacetime leading from to In this case, too, the corresponding classical system follows a geodesic of the geometry defined by the action differential which now depends on spatial coordinates, one time coordinate, and the corresponding differentials.
The statement that a classical system follows a geodesic of the geometry defined by its action, is often referred to as the principle of least action. A more appropriate name is principle of stationary action.
Energy and momentum
editObserve that if does not depend on (that is, ) then
is constant along geodesics. (We'll discover the reason for the negative sign in a moment.)
Likewise, if does not depend on (that is, ) then
is constant along geodesics.
tells us how much the projection of a segment of a path onto the time axis contributes to the action of tells us how much the projection of onto space contributes to If has no explicit time dependence, then equal intervals of the time axis make equal contributions to and if has no explicit space dependence, then equal intervals of any spatial axis make equal contributions to In the former case, equal time intervals are physically equivalent: they represent equal durations. In the latter case, equal space intervals are physically equivalent: they represent equal distances.
If equal intervals of the time coordinate or equal intervals of a space coordinate are not physically equivalent, this is so for either of two reasons. The first is that non-inertial coordinates are used. For if inertial coordinates are used, then every freely moving point mass moves by equal intervals of the space coordinates in equal intervals of the time coordinate, which means that equal coordinate intervals are physically equivalent. The second is that whatever it is that is moving is not moving freely: something, no matter what, influences its motion, no matter how. This is because one way of incorporating effects on the motion of an object into the mathematical formalism of quantum physics, is to make inertial coordinate intervals physically inequivalent, by letting depend on and/or
Thus for a freely moving classical object, both and are constant. Since the constancy of follows from the physical equivalence of equal intervals of coordinate time (a.k.a. the "homogeneity" of time), and since (classically) energy is defined as the quantity whose constancy is implied by the homogeneity of time, is the object's energy.
By the same token, since the constancy of follows from the physical equivalence of equal intervals of any spatial coordinate axis (a.k.a. the "homogeneity" of space), and since (classically) momentum is defined as the quantity whose constancy is implied by the homogeneity of space, is the object's momentum.
Let us differentiate a former result,
with respect to The left-hand side becomes
while the right-hand side becomes just Setting and using the above definitions of and we obtain
is a 4-scalar. Since are the components of a 4-vector, the left-hand side, is a 4-scalar if and only if are the components of another 4-vector.
(If we had defined without the minus, this 4-vector would have the components )
In the rest frame of a free point mass, and Using the Lorentz transformations, we find that this equals
where is the velocity of the point mass in Compare with the above framed equation to find that for a free point mass,
Lorentz force law
editTo incorporate effects on the motion of a particle (regardless of their causes), we must modify the action differential that a free particle associates with a path segment In doing so we must take care that the modified (i) remains homogeneous in the differentials and (ii) remains a 4-scalar. The most straightforward way to do this is to add a term that is not just homogeneous but linear in the coordinate differentials:
Believe it or not, all classical electromagnetic effects (as against their causes) are accounted for by this expression. is a scalar field (that is, a function of time and space coordinates that is invariant under rotations of the space coordinates), is a 3-vector field, and is a 4-vector field. We call and the scalar potential and the vector potential, respectively. The particle-specific constant is the electric charge, which determines how strongly a particle of a given species is affected by influences of the electromagnetic kind.
If a point mass is not free, the expressions at the end of the previous section give its kinetic energy and its kinetic momentum Casting (*) into the form
and plugging it into the definitions
we obtain
and are the particle's potential energy and potential momentum, respectively.
Now we plug (**) into the geodesic equation
For the right-hand side we obtain
while the left-hand side works out at
Two terms cancel out, and the final result is
As a classical object travels along the segment of a geodesic, its kinetic momentum changes by the sum of two terms, one linear in the temporal component of and one linear in the spatial component How much contributes to the change of depends on the electric field and how much contributes depends on the magnetic field The last equation is usually written in the form
called the Lorentz force law, and accompanied by the following story: there is a physical entity known as the electromagnetic field, which is present everywhere, and which exerts on a charge an electric force and a magnetic force
(Note: This form of the Lorentz force law holds in the Gaussian system of units. In the MKSA system of units the is missing.)
Whence the classical story?
editImagine a small rectangle in spacetime with corners
Let's calculate the electromagnetic contribution to the action of the path from to via for a unit charge () in natural units ( ):
Next, the contribution to the action of the path from to via :
Look at the difference:
Alternatively, you may think of as the electromagnetic contribution to the action of the loop
Let's repeat the calculation for a small rectangle with corners
Thus the electromagnetic contribution to the action of this loop equals the flux of through the loop.
Remembering (i) Stokes' theorem and (ii) the definition of in terms of we find that
In (other) words, the magnetic flux through a loop (or through any surface bounded by ) equals the circulation of around the loop (or around any surface bounded by the loop).
The effect of a circulation around the finite rectangle is to increase (or decrease) the action associated with the segment relative to the action associated with the segment If the actions of the two segments are equal, then we can expect the path of least action from to to be a straight line. If one segment has a greater action than the other, then we can expect the path of least action from to to curve away from the segment with the larger action.
Compare this with the classical story, which explains the curvature of the path of a charged particle in a magnetic field by invoking a force that acts at right angles to both the magnetic field and the particle's direction of motion. The quantum-mechanical treatment of the same effect offers no such explanation. Quantum mechanics invokes no mechanism of any kind. It simply tells us that for a sufficiently massive charge traveling from to the probability of finding that it has done so within any bundle of paths not containing the action-geodesic connecting with is virtually 0.
Much the same goes for the classical story according to which the curvature of the path of a charged particle in a spacetime plane is due to a force that acts in the direction of the electric field. (Observe that curvature in a spacetime plane is equivalent to acceleration or deceleration. In particular, curvature in a spacetime plane containing the axis is equivalent to acceleration in a direction parallel to the axis.) In this case the corresponding circulation is that of the 4-vector potential around a spacetime loop.
Schrödinger at last
editThe Schrödinger equation is non-relativistic. We obtain the non-relativistic version of the electromagnetic action differential,
by expanding the root and ignoring all but the first two terms:
This is obviously justified if which defines the non-relativistic regime.
Writing the potential part of as makes it clear that in most non-relativistic situations the effects represented by the vector potential are small compared to those represented by the scalar potential If we ignore them (or assume that vanishes), and if we include the charge in the definition of (or assume that ), we obtain
for the action associated with a spacetime path
Because the first term is the same for all paths from to it has no effect on the differences between the phases of the amplitudes associated with different paths. By dropping it we change neither the classical phenomena (inasmuch as the extremal path remains the same) nor the quantum phenomena (inasmuch as interference effects only depend on those differences). Thus
We now introduce the so-called wave function as the amplitude of finding our particle at if the appropriate measurement is made at time accordingly, is the amplitude of finding the particle first at (at time ) and then at (at time ). Integrating over we obtain the amplitude of finding the particle at (at time ), provided that Rule B applies. The wave function thus satisfies the equation
We again simplify our task by pretending that space is one-dimensional. We further assume that and differ by an infinitesimal interval Since is infinitesimal, there is only one path leading from to We can therefore forget about the path integral except for a normalization factor implicit in the integration measure and make the following substitutions:
This gives us
We obtain a further simplification if we introduce and integrate over instead of (The integration "boundaries" and are the same for both and ) We now have that
Since we are interested in the limit we expand all terms to first order in To which power in should we expand? As increases, the phase increases at an infinite rate (in the limit ) unless is of the same order as In this limit, higher-order contributions to the integral cancel out. Thus the left-hand side expands to
while expands to
The following integrals need to be evaluated:
The results are
Putting Humpty Dumpty back together again yields
The factor of must be the same on both sides, so which reduces Humpty Dumpty to
Multiplying by and taking the limit (which is trivial since has dropped out), we arrive at the Schrödinger equation for a particle with one degree of freedom subject to a potential :
Trumpets please! The transition to three dimensions is straightforward:
The Schrödinger equation: implications and applications
editIn this chapter we take a look at some of the implications of the Schrödinger equation
How fuzzy positions get fuzzier
editWe will calculate the rate at which the fuzziness of a position probability distribution increases, in consequence of the fuzziness of the corresponding momentum, when there is no counterbalancing attraction (like that between the nucleus and the electron in atomic hydrogen).
Because it is easy to handle, we choose a Gaussian function
which has a bell-shaped graph. It defines a position probability distribution
If we normalize this distribution so that then and
We also have that
- the Fourier transform of is
- this defines the momentum probability distribution
- and
The fuzziness of the position and of the momentum of a particle associated with is therefore the minimum allowed by the "uncertainty" relation:
Now recall that
where This has the Fourier transform
and this defines the position probability distribution
Comparison with reveals that Therefore,
The graphs below illustrate how rapidly the fuzziness of a particle the mass of an electron grows, when compared to an object the mass of a molecule or a peanut. Here we see one reason, though by no means the only one, why for all intents and purposes "once sharp, always sharp" is true of the positions of macroscopic objects.
Above: an electron with nanometer. In a second, grows to nearly 60 km.
Below: an electron with centimeter. grows only 16% in a second.
Next, a molecule with nanometer. In a second, grows to 4.4 centimeters.
Finally, a peanut (2.8 g) with nanometer. takes the present age of the universe to grow to 7.5 micrometers.
Time-independent Schrödinger equation
editIf the potential V does not depend on time, then the Schrödinger equation has solutions that are products of a time-independent function and a time-dependent phase factor :
Because the probability density is independent of time, these solutions are called stationary.
Plug into
to find that satisfies the time-independent Schrödinger equation
Why energy is quantized
editLimiting ourselves again to one spatial dimension, we write the time independent Schrödinger equation in this form:
Since this equation contains no complex numbers except possibly itself, it has real solutions, and these are the ones in which we are interested. You will notice that if then is positive and has the same sign as its second derivative. This means that the graph of curves upward above the axis and downward below it. Thus it cannot cross the axis. On the other hand, if then is negative and and its second derivative have opposite signs. In this case the graph of curves downward above the axis and upward below it. As a result, the graph of keeps crossing the axis — it is a wave. Moreover, the larger the difference the larger the curvature of the graph; and the larger the curvature, the smaller the wavelength. In particle terms, the higher the kinetic energy, the higher the momentum.
Let us now find the solutions that describe a particle "trapped" in a potential well — a bound state. Consider this potential:
Observe, to begin with, that at and where the slope of does not change since at these points. This tells us that the probability of finding the particle cannot suddenly drop to zero at these points. It will therefore be possible to find the particle to the left of or to the right of where classically it could not be. (A classical particle would oscillates back and forth between these points.)
Next, take into account that the probability distributions defined by must be normalizable. For the graph of this means that it must approach the axis asymptotically as
Suppose that we have a normalized solution for a particular value If we increase or decrease the value of the curvature of the graph of between and increases or decreases. A small increase or decrease won't give us another solution: won't vanish asymptotically for both positive and negative To obtain another solution, we must increase by just the right amount to increase or decrease by one the number of wave nodes between the "classical" turning points and and to make again vanish asymptotically in both directions.
The bottom line is that the energy of a bound particle — a particle "trapped" in a potential well — is quantized: only certain values yield solutions of the time-independent Schrödinger equation:
A quantum bouncing ball
editAs a specific example, consider the following potential:
is the gravitational acceleration at the floor. For the Schrödinger equation as given in the previous section tells us that unless The only sensible solution for negative is therefore The requirement that for ensures that our perfectly elastic, frictionless quantum bouncer won't be found below the floor.
Since a picture is worth more than a thousand words, we won't solve the time-independent Schrödinger equation for this particular potential but merely plot its first eight solutions:
Where would a classical bouncing ball subject to the same potential reverse its direction of motion? Observe the correlation between position and momentum (wavenumber).
All of these states are stationary; the probability of finding the quantum bouncer in any particular interval of the axis is independent of time. So how do we get it to move?
Recall that any linear combination of solutions of the Schrödinger equation is another solution. Consider this linear combination of two stationary states:
Assuming that the coefficients and the wave functions are real, we calculate the mean position of a particle associated with :
The first two integrals are the (time-independent) mean positions of a particle associated with and respectively. The last term equals
and this tells us that the particle's mean position oscillates with frequency and amplitude about the sum of the first two terms.
Visit this site to watch the time-dependence of the probability distribution associated with a quantum bouncer that is initially associated with a Gaussian distribution.
Atomic hydrogen
editWhile de Broglie's theory of 1923 featured circular electron waves, Schrödinger's "wave mechanics" of 1926 features standing waves in three dimensions. Finding them means finding the solutions of the time-independent Schrödinger equation
with the potential energy of a classical electron at a distance from the proton. (Only when we come to the relativistic theory will we be able to shed the last vestige of classical thinking.)
In using this equation, we ignore (i) the influence of the electron on the proton, whose mass is some 1836 times larger than that of he electron, and (ii) the electron's spin. Since relativistic and spin effects on the measurable properties of atomic hydrogen are rather small, this non-relativistic approximation nevertheless gives excellent results.
For bound states the total energy is negative, and the Schrödinger equation has a discrete set of solutions. As it turns out, the "allowed" values of are precisely the values that Bohr obtained in 1913:
However, for each there are now linearly independent solutions. (If are independent solutions, then none of them can be written as a linear combination of the others.)
Solutions with different correspond to different energies. What physical differences correspond to linearly independent solutions with the same ?

Using polar coordinates, one finds that all solutions for a particular value are linear combinations of solutions that have the form
turns out to be another quantized variable, for implies that with In addition, has an upper bound, as we shall see in a moment.
Just as the factorization of into made it possible to obtain a -independent Schrödinger equation, so the factorization of into makes it possible to obtain a -independent Schrödinger equation. This contains another real parameter over and above whose "allowed" values are given by with an integer satisfying The range of possible values for is bounded by the inequality The possible values of the principal quantum number the angular momentum quantum number and the so-called magnetic quantum number thus are:
Each possible set of quantum numbers defines a unique wave function and together these make up a complete set of bound-state solutions () of the Schrödinger equation with The following images give an idea of the position probability distributions of the first three states (not to scale). Below them are the probability densities plotted against Observe that these states have nodes, all of which are spherical, that is, surfaces of constant (The nodes of a wave in three dimensions are two-dimensional surfaces. The nodes of a "probability wave" are the surfaces at which the sign of changes and, consequently, the probability density vanishes.)
Take another look at these images:
The letters s,p,d,f stand for l=0,1,2,3, respectively. (Before the quantum-mechanical origin of atomic spectral lines was understood, a distinction was made between "sharp," "principal," "diffuse," and "fundamental" lines. These terms were subsequently found to correspond to the first four values that can take. From onward the labels follows the alphabet: f,g,h...) Observe that these states display both spherical and conical nodes, the latter being surfaces of constant (The "conical" node with is a horizontal plane.) These states, too, have a total of nodes, of which are conical.
Because the "waviness" in is contained in a phase factor it does not show up in representations of To make it visible, the phase can be encoded as color:
In chemistry it is customary to consider real superpositions of opposite like as in the following images, which are also valid solutions.
-
or
-
or
-
or
-
-
or
-
-
-
The total number of nodes is again the total number of non-spherical nodes is again but now there are plane nodes containing the axis and conical nodes.
What is so special about the axis? Absolutely nothing, for the wave functions which are defined with respect to a different axis, make up another complete set of bound-state solutions. This means that every wave function can be written as a linear combination of the functions and vice versa.
Observables and operators
editRemember the mean values
As noted already, if we define the operators
- ("multiply with ") and
then we can write
By the same token,
Which observable is associated with the differential operator ? If and are constant (as the partial derivative with respect to requires), then is constant, and
Given that and this works out at or
Since, classically, orbital angular momentum is given by so that it seems obvious that we should consider as the operator associated with the component of the atom's angular momentum.
Yet we need to be wary of basing quantum-mechanical definitions on classical ones. Here are the quantum-mechanical definitions:
Consider the wave function of a closed system with degrees of freedom. Suppose that the probability distribution (which is short for ) is invariant under translations in time: waiting for any amount of time makes no difference to it:
Then the time dependence of is confined to a phase factor
Further suppose that the time coordinate and the space coordinates are homogeneous — equal intervals are physically equivalent. Since is closed, the phase factor cannot then depend on and its phase can at most linearly depend on waiting for should have the same effect as twice waiting for In other words, multiplying the wave function by should have same effect as multiplying it twice by :
Thus
So the existence of a constant ("conserved") quantity or (in conventional units) is implied for a closed system, and this is what we mean by the energy of the system.
Now suppose that is invariant under translations in the direction of one of the spatial coordinates say :
Then the dependence of on is confined to a phase factor
And suppose again that the time coordinates and are homogeneous. Since is closed, the phase factor cannot then depend on or and its phase can at most linearly depend on : translating by should have the same effect as twice translating it by In other words, multiplying the wave function by should have same effect as multiplying it twice by :
Thus
So the existence of a constant ("conserved") quantity or (in conventional units) is implied for a closed system, and this is what we mean by the j-component of the system's momentum.
You get the picture. Moreover, the spatial coordinates might as well be the spherical coordinates If is invariant under rotations about the axis, and if the longitudinal coordinate is homogeneous, then
In this case we call the conserved quantity the component of the system's angular momentum.
Now suppose that is an observable, that is the corresponding operator, and that satisfies
We say that is an eigenfunction or eigenstate of the operator and that it has the eigenvalue Let's calculate the mean and the standard deviation of for We obviously have that
Hence
since For a system associated with is dispersion-free. Hence the probability of finding that the value of lies in an interval containing is 1. But we have that
So, indeed, is the operator associated with the component of the atom's angular momentum.
Observe that the eigenfunctions of any of these operators are associated with systems for which the corresponding observable is "sharp": the standard deviation measuring its fuzziness vanishes.
For obvious reasons we also have
If we define the commutator then saying that the operators and commute is the same as saying that their commutator vanishes. Later we will prove that two observables are compatible (can be simultaneously measured) if and only if their operators commute.
Exercise: Show that
One similarly finds that and The upshot: different components of a system's angular momentum are incompatible.
Exercise: Using the above commutators, show that the operator commutes with and
Beyond hydrogen: the Periodic Table
editIf we again assume that the nucleus is fixed at the center and ignore relativistic and spin effects, then the stationary states of helium are the solutions of the following equation:
The wave function now depends on six coordinates, and the potential energy is made up of three terms. and are associated with the respective distances of the electrons from the nucleus, and is associated with the distance between the electrons. Think of as the value the potential energy associated with the two electrons would have if they were at and respectively.
Why are there no separate wave functions for the two electrons? The joint probability of finding the first electron in a region and the second in a region (relative to the nucleus) is given by
If the probability of finding the first electron in were independent of the whereabouts of the second electron, then we could assign to it a wave function and if the probability of finding the second electron in were independent of the whereabouts of the first electron, we could assign to it a wave function In this case would be given by the product of the two wave functions, and would be the product of and But in general, and especially inside a helium atom, the positional probability distribution for the first electron is conditional on the whereabouts of the second electron, and vice versa, given that the two electrons repel each other (to use the language of classical physics).
For the lowest energy levels, the above equation has been solved by numerical methods. With three or more electrons it is hopeless to look for exact solutions of the corresponding Schrödinger equation. Nevertheless, the Periodic Table and many properties of the chemical elements can be understood by using the following approximate theory.
First,we disregard the details of the interactions between the electrons. Next, since the chemical properties of atoms depend on their outermost electrons, we consider each of these atoms subject to a potential that is due to (i) the nucleus and (ii) a continuous, spherically symmetric, charge distribution doing duty for the other electrons. We again neglect spin effects except that we take account of the Pauli exclusion principle, according to which the probability of finding two electrons (more generally, two fermions) having exactly the same properties is 0. Thus two electrons can be associated with exactly the same wave function provided that their spin states differ in the following way: whenever the spins of the two electrons are measured with respect to a given axis, the outcomes are perfectly anticorrelated; one will be "up" and the other will be "down". Since there are only two possible outcomes, a third electron cannot be associated with the same wave function.
This approximate theory yields stationary wave functions called orbitals for individual electrons. These are quite similar to the stationary wave functions one obtains for the single electron of hydrogen, except that their dependence on the radial coordinate is modified by the negative charge distribution representing the remaining electrons. As a consequence of this modification, the energies associated with orbitals with the same quantum number but different quantum numbers are no longer equal. For any given obitals with higher yield a larger mean distance between the electron and the nucleus, and the larger this distance, the more the negative charge of the remaining electrons screens the positive charge of the nucleus. As a result, an electron with higher is less strongly bound (given the same ), so its ionization energy is lower.
Chemists group orbitals into shells according to their principal quantum number. As we have seen, the -th shell can "accommodate" up to electrons. Helium has the first shell completely "filled" and the second shell "empty." Because the helium nucleus has twice the charge of the hydrogen nucleus, the two electrons are, on average, much nearer the nucleus than the single electron of hydrogen. The ionization energy of helium is therefore much larger, 2372.3 J/mol as compared to 1312.0 J/mol for hydrogen. On the other hand, if you tried to add an electron to create a negative helium ion, it would have to go into the second shell, which is almost completely screened from the nucleus by the electrons in the first shell. Helium is therefore neither prone to give up an electron not able to hold an extra electron. It is chemically inert, as are all elements in the rightmost column of the Periodic Table.
In the second row of the Periodic Table the second shell gets filled. Since the energies of the 2p orbitals are higher than that of the 2s orbital, the latter gets "filled" first. With each added electron (and proton!) the entire electron distribution gets pulled in, and the ionization energy goes up, from 520.2 J/mol for lithium (atomic number Z=3) to 2080.8 J/mol for neon (Z=10). While lithium readily parts with an electron, fluorine (Z=9) with a single empty "slot" in the second shell is prone to grab one. Both are therefore quite active chemically. The progression from sodium (Z=11) to argon (Z=18) parallels that from lithium to neon.
There is a noteworthy peculiarity in the corresponding sequences of ionization energies: The ionization energy of oxygen (Z=8, 1313.9 J/mol) is lower than that of nitrogen (Z=7, 1402.3 J/mol), and that of sulfur (Z=16, 999.6 J/mol) is lower than that of phosphorus (Z=15, 1011.8 J/mol). To understand why this is so, we must take account of certain details of the inter-electronic forces that we have so far ignored.
Suppose that one of the two 2p electrons of carbon (Z=6) goes into the orbital with respect to the axis. Where will the other 2p electron go? It will go into any vacant orbital that minimizes the repulsion between the two electrons, by maximizing their mean distance. This is neither of the orbitals with with respect to the axis but an orbital with with respect to some axis perpendicular to the axis. If we call this the axis, then the third 2p electron of nitrogen goes into the orbital with relative to axis. The fourth 2p electron of oxygen then has no choice but to go — with opposite spin — into an already occupied 2p orbital. This raises its energy significantly and accounts for the drop in ionization from nitrogen to oxygen.
By the time the 3p orbitals are "filled," the energies of the 3d states are pushed up so high (as a result of screening) that the 4s state is energetically lower. The "filling up" of the 3d orbitals therefore begins only after the 4s orbitals are "occupied," with scandium (Z=21).
Thus even this simplified and approximate version of the quantum theory of atoms has the power to predict the qualitative and many of the quantitative features of the Period Table.
Probability flux
editThe time rate of change of the probability density (at a fixed location ) is given by
With the help of the Schrödinger equation and its complex conjugate,
one obtains
The terms containing cancel out, so we are left with
Next, we calculate the divergence of :
The upshot:
Integrated over a spatial region with unchanging boundary
According to Gauss's law, the outward flux of through equals the integral of the divergence of over
We thus have that
If is the continuous density of some kind of stuff (stuff per unit volume) and is its flux (stuff per unit area per unit time), then on the left-hand side we have the rate at which the stuff inside increases, and on the right-hand side we have the rate at which stuff enters through the surface of So if some stuff moves from place A to place B, it crosses the boundary of any region that contains either A or B. This is why the framed equation is known as a continuity equation.
In the quantum world, however, there is no such thing as continuously distributed and/or continuously moving stuff. and respectively, are a density (something per unit volume) and a flux (something per unit area per unit time) only in a formal sense. If is the wave function associated with a particle, then the integral gives the probability of finding the particle in if the appropriate measurement is made, and the framed equation tells us this: if the probability of finding the particle inside as a function of the time at which the measurement is made, increases, then the probability of finding the particle outside as a function of the same time, decreases by the same amount. (Much the same holds if is associated with a system having degrees of freedom and is a region of the system's configuration space.) This is sometimes expressed by saying that "probability is (locally) conserved." When you hear this, then remember that the probability for something to happen in a given place at a given time isn't anything that is situated at that place or that exists at that time.
Entanglement (a preview)
editBell's theorem: the simplest version
editQuantum mechanics permits us to create the following scenario.
- Pairs of particles are launched in opposite directions.
- Each particle is subjected to one of three possible measurements (1, 2, or 3).
- Each time the two measurements are chosen at random.
- Each measurement has two possible results, indicated by a red or green light.
Here is what we find:
- If both particles are subjected to the same measurement, identical results are never obtained.
- The two sequences of recorded outcomes are completely random. In particular, half of the time both lights are the same color.
If this doesn't bother you, then please explain how it is that the colors differ whenever identical measurements are performed!
The obvious explanation would be that each particle arrives with an "instruction set" — some property that pre-determines the outcome of every possible measurement. Let's see what this entails.
Each particle arrives with one of the following 23 = 8 instruction sets:
- RRR, RRG, RGR, GRR, RGG, GRG, GGR, or GGG.
(If a particle arrives with, say, RGG, then the apparatus flashes red if it is set to 1 and green if it is set to 2 or 3.) In order to explain why the outcomes differ whenever both particles are subjected to the same measurement, we have to assume that particles launched together arrive with opposite instruction sets. If one carries the instruction (or arrives with the property denoted by) RRG, then the other carries the instruction GGR.
Suppose that the instruction sets are RRG and GGR. In this case we observe different colors with the following five of the 32 = 9 possible combinations of apparatus settings:
- 1—1, 2—2, 3—3, 1—2, and 2—1,
and we observe equal colors with the following four:
- 1—3, 2—3, 3—1, and 3—2.
Because the settings are chosen at random, this particular pair of instruction sets thus results in different colors 5/9 of the time. The same is true for the other pairs of instruction sets except the pair RRR, GGG. If the two particles carry these respective instruction sets, we see different colors every time. It follows that we see different colors at least 5/9 of the time.
But different colors are observed half of the time! In reality the probability of observing different colors is 1/2. Conclusion: the statistical predictions of quantum mechanics cannot be explained with the help of instruction sets. In other words, these measurements do not reveal pre-existent properties. They create the properties the possession of which they indicate.
Then how is it that the colors differ whenever identical measurements are made? How does one apparatus "know" which measurement is performed and which outcome is obtained by the other apparatus?
Whenever the joint probability p(A,B) of the respective outcomes A and B of two measurements does not equal the product p(A) p(B) of the individual probabilities, the outcomes — or their probabilities — are said to be correlated. With equal apparatus settings we have p(R,R) = p(G,G) = 0, and this obviously differs from the products p(R) p(R) and p(G) p(G), which equal What kind of mechanism is responsible for the correlations between the measurement outcomes?
- You understand this as much as anybody else!
The conclusion that we see different colors at least 5/9 of the time is Bell's theorem (or Bell's inequality) for this particular setup. The fact that the universe violates the logic of Bell's Theorem is evidence that particles do not carry instruction sets embedded within them and instead have instantaneous knowledge of other particles at a great distance. Here is a comment by a distinguished Princeton physicist as quoted by David Mermin[1]
- Anybody who's not bothered by Bell's theorem has to have rocks in his head.
And here is why Einstein wasn't happy with quantum mechanics:
- I cannot seriously believe in it because it cannot be reconciled with the idea that physics should represent a reality in time and space, free from spooky actions at a distance.[2]
Sadly, Einstein (1879 - 1955) did not know Bell's theorem of 1964. We know now that
- there must be a mechanism whereby the setting of one measurement device can influence the reading of another instrument, however remote.[3]
- Spooky actions at a distance are here to stay!
- ↑ N. David Mermin, "Is the Moon there when nobody looks? Reality and the quantum theory," Physics Today, April 1985. The version of Bell's theorem discussed in this section first appeared in this article.
- ↑ Albert Einstein, The Born-Einstein Letters, with comments by Max Born (New York: Walker, 1971).
- ↑ John S. Bell, "On the Einstein Podolsky Rosen paradox," Physics 1, pp. 195-200, 1964.
A quantum game
editHere are the rules:[1]
- Two teams play against each other: Andy, Bob, and Charles (the "players") versus the "interrogators".
- Each player is asked either "What is the value of X?" or "What is the value of Y?"
- Only two answers are allowed: +1 or −1.
- Either each player is asked the X question, or one player is asked the X question and the two other players are asked the Y question.
- The players win if the product of their answers is −1 in case only X questions are asked, and if the product of their answers is +1 in case Y questions are asked. Otherwise they lose.
- The players are not allowed to communicate with each other once the questions are asked. Before that, they are permitted to work out a strategy.
Is there a failsafe strategy? Can they make sure that they will win? Stop to ponder the question.
Let us try pre-agreed answers, which we will call XA, XB, XC and YA, YB, YC. The winning combinations satisfy the following equations:
Consider the first three equations. The product of their right-hand sides equals +1. The product of their left-hand sides equals XAXBXC, implying that XAXBXC = 1. (Remember that the possible values are ±1.) But if XAXBXC = 1, then the fourth equation XAXBXC = −1 obviously cannot be satisfied.
- The bottom line: There is no failsafe strategy with pre-agreed answers.
- ↑ Lev Vaidman, "Variations on the theme of the Greenberger-Horne-Zeilinger proof," Foundations of Physics 29, pp. 615-30, 1999.
The experiment of Greenberger, Horne, and Zeilinger
editAnd yet there is a failsafe strategy.[1]
Here goes:
- Andy, Bob, and Charles prepare three particles (for instance, electrons) in a particular way. As a result, they are able to predict the probabilities of the possible outcomes of any spin measurement to which the three particles may subsequently be subjected. In principle these probabilities do not depend on how far the particles are apart.
- Each player takes one particle with him.
- Whoever is asked the X question measures the x component of the spin of his particle and answers with his outcome, and whoever is asked the Y question measures the y component of the spin of his particle and answers likewise. (All you need to know at this point about the spin of a particle is that its component with respect to any one axis can be measured, and that for the type of particle used by the players there are two possible outcomes, namely +1 and −1.
Proceeding in this way, the team of players is sure to win every time.
Is it possible for the x and y components of the spins of the three particles to be in possession of values before their values are actually measured?
Suppose that the y components of the three spins have been measured. The three equations
of the previous section tell us what we would have found if the x component of any one of the three particles had been measured instead of the y component. If we assume that the x components are in possession of values even though they are not measured, then their values can be inferred from the measured values of the three y components.
Try to fill in the following table in such a way that
- each cell contains either +1 or −1,
- the product of the three X values equals −1, and
- the product of every pair of Y values equals the remaining X value.
Can it be done?
| A | B | C | |
|---|---|---|---|
| X | |||
| Y |
The answer is negative, for the same reason that the four equations
cannot all be satisfied. Just as there can be no strategy with pre-agreed answers, there can be no pre-existent values. We seem to have no choice but to conclude that these spin components are in possession of values only if (and only when) they are actually measured.
Any two outcomes suffice to predict a third outcome. If two x components are measured, the third x component can be predicted, if two y components are measured, the x component of the third spin can be predicted, and if one x and one y component are measurement, the y component of the third spin can be predicted. How can we understand this given that
- the values of the spin components are created as and when they are measured,
- the relative times of the measurements are irrelevant,
- in principle the three particles can be millions of miles apart.
How does the third spin "know" which components of the other spins are measured and which outcomes are obtained? What mechanism correlates the outcomes?
- You understand this as much as anybody else!
- ↑ D. M. Greenberger, M. A. Horne, and A. Zeilinger, "Going beyond Bell's theorem," in Bell's theorem, Quantum Theory, and Conception of the Universe, edited by M. Kafatos (Dordrecht: Kluwer Academic, 1989), pp. 69-72.
Authors
editList authors here.
Appendix
editProbability
editBasic Concepts
editProbability is a numerical measure of likelihood. If an event has a probability equal to 1 (or 100%), then it is certain to occur. If it has a probability equal to 0, then it will definitely not occur. And if it has a probability equal to 1/2 (or 50%), then it is as likely as not to occur.
You will know that tossing a fair coin has probability 1/2 to yield heads, and that casting a fair die has probability 1/6 to yield a 1. How do we know this?
There is a principle known as the principle of indifference, which states: if there are n mutually exclusive and jointly exhaustive possibilities, and if, as far as we know, there are no differences between the n possibilities apart from their names (such as "heads" or "tails"), then each possibility should be assigned a probability equal to 1/n. (Mutually exclusive: only one possibility can be realized in a single trial. Jointly exhaustive: at least one possibility is realized in a single trial. Mutually exclusive and jointly exhaustive: exactly ony possibility is realized in a single trial.)
Since this principle appeals to what we know, it concerns epistemic probabilities (a.k.a. subjective probabilities) or degrees of belief. If you are certain of the truth of a proposition, then you assign to it a probability equal to 1. If you are certain that a proposition is false, then you assign to it a probability equal to 0. And if you have no information that makes you believe that the truth of a proposition is more likely (or less likely) than its falsity, then you assign to it probability 1/2. Subjective probabilities are therefore also known as ignorance probabilities: if you are ignorant of any differences between the possibilities, you assign to them equal probabilities.
If we assign probability 1 to a proposition because we believe that it is true, we assign a subjective probability, and if we assign probability 1 to an event because it is certain that it will occur, we assign an objective probability. Until the advent of quantum mechanics, the only objective probabilities known were relative frequencies.
The advantage of the frequentist definition of probability is that it allows us to measure probabilities, at least approximately. The trouble with it is that it refers to ensembles. You can't measure the probability of heads by tossing a single coin. You get better and better approximations to the probability of heads by tossing a larger and larger number of coins and dividing the number of heads by The exact probability of heads is the limit
The meaning of this formula is that for any positive number however small, you can find a (sufficiently large but finite) number such that
The probability that events from a mutually exclusive and jointly exhaustive set of possible events happen is the sum of the probabilities of the events. Suppose, for example, you win if you cast either a 1 or a 6. The probability of winning is
In frequentist terms, this is virtually self-evident. approximates approximates and approximates
The probability that two independent events happen is the product of the probabilities of the individual events. Suppose, for example, you cast two dice and you win if the total is 12. Then
By the principle of indifference, there are now equiprobable possibilities, and casting a total of 12 with two dice is one of them.
It is important to remember that the joint probability of two events equals the product of the individual probabilities and only if the two events are independent, meaning that the probability of one does not depend on whether or not the other happens. In terms of propositions: the probability that the conjunction is true is the probability that is true times the probability that is true only if the probability that either proposition is true does not depend on whether the other is true or false. Ignoring this can have the most tragic consequences.
The general rule for the joint probability of two events is
is a conditional probability: the probability of given that
To see this, let be the number of trials in which both and happen or are true. approximates approximates and approximates But
An immediate consequence of this is Bayes' theorem:
The following is just as readily established:
where happens or is true whenever does not happen or is false. The generalization to mutually exclusive and jointly exhaustive possibilities should be obvious.
Given a random variable, which is a set of random numbers, we may want to know the arithmetic mean
as well as the standard deviation, which is the root-mean-square deviation from the arithmetic mean,
The standard deviation is an important measure of statistical dispersion.
Given possible measurement outcomes with probabilities we have a probability distribution and we may want to know the expected value of defined by
as well as the corresponding standard deviation
which is a handy measure of the fuzziness of .
We have defined probability as a numerical measure of likelihood. So what is likelihood? What is probability apart from being a numerical measure? The frequentist definition covers some cases, the epistemic definition covers others, but which definition would cover all cases? It seems that probability is one of those concepts that are intuitively meaningful to us, but — just like time or the experience of purple — cannot be explained in terms of other concepts.
Some Problems
editProblem 1 (Monty Hall). A player in a game show is given the choice of three doors. Behind one door is the Grand Prize (say, a car); behind the other two doors are booby prizes (say, goats). The player picks a door, and the show host peeks behind the doors and opens one of the remaining doors. There is a booby prize behind the door he opened. The host then offers the player either to stay with the door that was chosen at the beginning, or to switch to the other closed door. What gives the player the better chance of winning: to switch doors or to stay with the original choice? Or are the chances equal?
Problem 2. Imagine you toss a coin successively and wait till the first time the pattern HTT appears. For example, if the sequence of tosses was
- H H T H H T H H T T H H T T T H T H
then the pattern HTT would appear after the 10th toss. Let A(HTT) be the average number of tosses until HTT occurs, and let A(HTH) be the average number of tosses until HTH occurs. Which of the following is true?
- (a) A( HTH) < ( HTT), (b) A(HTH) = A(HTT), or (c) A(HTH) > A(HTT).
Problem 3. Imagine a test for a certain disease (say, HIV) that is 99% accurate. And suppose a person picked at random tests positive. What is the probability that the person actually has the disease?
Solutions
editProblem 1. Let be the probability that the car is behind door 1, the probability that the host opens door 3, and the probability that the host opens door 3 given that the car is behind door 1. We have
as well as
If the first choice is door 1, then and Hence
and thus
In words: If the player's first choice is door 1 and the host opens door 3, then the probability that the car is behind door 2 is whereas the probability that it is behind door 1 is 1 – 2/3 = 1/3. A quicker way to see that switching doubles the chances of winning is to compare this game with another one, in which the show host offers the choice of either opening the originally chosen door or opening both other doors (and winning regardless of which, if any, has the car).
Note: This result depends on the show host *deliberately* opening only a door with a goat behind it. If she doesn't know - or doesn't care (!) - which door the car is behind, and opens a remaining door at random, then 1/3 of the outcomes that were initially possible have been removed by her having opened a door with a goat. In this case the player gains no advantage (or disadvantage) by switching. So the answer depends on the rules of the game, not just the sequence of events. Of course the player may not know what the 'rules' are in this respect, in which case he should still switch doors because there can be no disadvantage in doing so.
Problem 2. The average number of tosses until HTT occurs, A(HTT), equals 8, whereas A(HTH) = 10. To see why the latter is greater, imagine you have tossed HT. If you are looking for HTH and the next toss gives you HTT, then your next chance to see HTH is after a total of 6 tosses, whereas if you are looking for HTT and the next toss gives you HTH, then your next chance to see HTT is after a total of 5 tosses.
Problem 3. The answer depends on how rare the disease is. Suppose that one in 10,000 has it. This means 100 in a million. If a million are tested, there will be 99 true positives and one false negative. 99% of the remaining 999,900 — that is, 989,901 — will yield true negatives and 1% — that is, 9,999 — will yield false positives. The probability that a randomly picked person testing positive actually has the disease is the number of true positives divided by the number of positives, which in this particular example is 99/(9999+99) = 0.0098 — less than 1%!
Moral
editBe it scientific data or evidence in court — there are usually competing explanations, and usually each explanation has a likely bit and an unlikely bit. For example, having the disease is unlikely, but the test is likely to be correct; not having the disease is likely, but a false test result is unlikely. You can see the importance of accurate assessments of the likelihood of competing explanations, and if you have tried the problems, you have seen that we aren't very good at such assessments.
Mathematical tools
editElements of calculus
editA definite integral
editImagine an object that is free to move in one dimension — say, along the axis. Like every physical object, it has a more or less fuzzy position (relative to whatever reference object we choose). For the purpose of describing its fuzzy position, quantum mechanics provides us with a probability density This depends on actual measurement outcomes, and it allows us to calculate the probability of finding the particle in any given interval of the axis, provided that an appropriate measurement is made. (Remember our mantra: the mathematical formalism of quantum mechanics serves to assign probabilities to possible measurement outcomes on the basis of actual outcomes.)
We call a probability density because it represents a probability per unit length. The probability of finding in the interval between and is given by the area between the graph of the axis, and the vertical lines at and respectively.
How do we calculate this area? The trick is to cover it with narrow rectangles of width
The area of the first rectangle from the left is the area of the second is and the area of the last is For the sum of these areas we have the shorthand notation
It is not hard to visualize that if we increase the number of rectangles and at the same time decrease the width of each rectangle, then the sum of the areas of all rectangles fitting under the graph of between and gives us a better and better approximation to the area and thus to the probability of finding in the interval between and As tends toward 0 and tends toward infinity (), the above sum tends toward the integral
We sometimes call this a definite integral to emphasize that it's just a number. (As you can guess, there are also indefinite integrals, which you will learn more about later.) The uppercase delta has turned into a indicating that is an infinitely small (or infinitesimal) width, and the summation symbol (the uppercase sigma) has turned into an elongated S indicating that we are adding infinitely many infinitesimal areas.
Don't let the term "infinitesimal" scare you. An infinitesimal quantity means nothing by itself. It is the combination of the integration symbol with the infinitesimal quantity that makes sense as a limit, in which grows above any number however large, (and hence the area of each rectangle) shrinks below any (positive) number however small, while the sum of the areas tends toward a well-defined, finite number.
Differential calculus: a very brief introduction
editAnother method by which we can obtain a well-defined, finite number from infinitesimal quantities is to divide one such quantity by another.
We shall assume throughout that we are dealing with well-behaved functions, which means that you can plot the graph of such a function without lifting up your pencil, and you can do the same with each of the function's derivatives. So what is a function, and what is the derivative of a function?
A function is a machine with an input and an output. Insert a number and out pops the number Rather confusingly, we sometimes think of not as a machine that churns out numbers but as the number churned out when is inserted.
The (first) derivative of is a function that tells us how much increases as increases (starting from a given value of say ) in the limit in which both the increase in and the corresponding increase in (which of course may be negative) tend toward 0:
The above diagrams illustrate this limit. The ratio is the slope of the straight line through the black circles (that is, the of the angle between the positive axis and the straight line, measured counterclockwise from the positive axis). As decreases, the black circle at slides along the graph of towards the black circle at and the slope of the straight line through the circles increases. In the limit the straight line becomes a tangent on the graph of touching it at The slope of the tangent on at is what we mean by the slope of at
So the first derivative of is the function that equals the slope of for every To differentiate a function is to obtain its first derivative By differentiating we obtain the second derivative of by differentiating we obtain the third derivative and so on.
It is readily shown that if is a number and and are functions of then
- and
A slightly more difficult problem is to differentiate the product of two functions of Think of and as the vertical and horizontal sides of a rectangle of area As increases by the product increases by the sum of the areas of the three white rectangles in this diagram:
In other "words",
and thus
If we now take the limit in which and, hence, and tend toward 0, the first two terms on the right-hand side tend toward What about the third term? Because it is the product of an expression (either or ) that tends toward 0 and an expression (either or ) that tends toward a finite number, it tends toward 0. The bottom line:
This is readily generalized to products of functions. Here is a special case:
Observe that there are equal terms between the two equal signs. If the function returns whatever you insert, this boils down to
Now suppose that is a function of and is a function of An increase in by causes an increase in by and this in turn causes an increase in by Thus In the limit the becomes a :
We obtained for integers Obviously it also holds for and
- Show that it also holds for negative integers Hint: Use the product rule to calculate
- Show that Hint: Use the product rule to calculate
- Show that also holds for where is a natural number.
- Show that this equation also holds if is a rational number. Use
Since every real number is the limit of a sequence of rational numbers, we may now confidently proceed on the assumption that holds for all real numbers
Taylor series
editA well-behaved function can be expanded into a power series. This means that for all non-negative integers there are real numbers such that
Let us calculate the first four derivatives using :
Setting equal to zero, we obtain
Let us write for the -th derivative of We also write — think of as the "zeroth derivative" of We thus arrive at the general result where the factorial is defined as equal to 1 for and and as the product of all natural numbers for Expressing the coefficients in terms of the derivatives of at we obtain
This is the Taylor series for
A remarkable result: if you know the value of a well-behaved function and the values of all of its derivatives at the single point then you know at all points Besides, there is nothing special about so is also determined by its value and the values of its derivatives at any other point :
The exponential function
editWe define the function by requiring that
- and
The value of this function is everywhere equal to its slope. Differentiating the first defining equation repeatedly we find that
The second defining equation now tells us that for all The result is a particularly simple Taylor series:
Let us check that a well-behaved function satisfies the equation
if and only if
We will do this by expanding the 's in powers of and and compare coefficents. We have
and using the binomial expansion
we also have that
Voilà.
The function obviously satisfies and hence
So does the function
Moreover, implies
We gather from this
- that the functions satisfying form a one-parameter family, the parameter being the real number and
- that the one-parameter family of functions satisfies , the parameter being the real number
But also defines a one-parameter family of functions that satisfies , the parameter being the positive number
Conclusion: for every real number there is a positive number (and vice versa) such that
One of the most important numbers is defined as the number for which that is: :
The natural logarithm is defined as the inverse of so Show that
Hint: differentiate
The indefinite integral
editHow do we add up infinitely many infinitesimal areas? This is elementary if we know a function of which is the first derivative. If then and
All we have to do is to add up the infinitesimal amounts by which increases as increases from to and this is simply the difference between and
A function of which is the first derivative is called an integral or antiderivative of Because the integral of is determined only up to a constant, it is also known as indefinite integral of Note that wherever is negative, the area between its graph and the axis counts as negative.
How do we calculate the integral if we don't know any antiderivative of the integrand ? Generally we look up a table of integrals. Doing it ourselves calls for a significant amount of skill. As an illustration, let us do the Gaussian integral
For this integral someone has discovered the following trick. (The trouble is that different integrals generally require different tricks.) Start with the square of :
This is an integral over the plane. Instead of dividing this plane into infinitesimal rectangles we may divide it into concentric rings of radius and infinitesimal width Since the area of such a ring is we have that
Now there is only one integration to be done. Next we make use of the fact that hence and we introduce the variable :
Since we know that the antiderivative of is we also know that
Therefore and
Believe it or not, a significant fraction of the literature in theoretical physics concerns variations and elaborations of this basic Gaussian integral.
One variation is obtained by substituting for :
Another variation is obtained by thinking of both sides of this equation as functions of and differentiating them with respect to The result is
Sine and cosine
editWe define the function by requiring that
- and
If you sketch the graph of this function using only this information, you will notice that wherever is positive, its slope decreases as increases (that is, its graph curves downward), and wherever is negative, its slope increases as increases (that is, its graph curves upward).
Differentiating the first defining equation repeatedly yields
for all natural numbers Using the remaining defining equations, we find that equals 1 for k = 0,4,8,12…, –1 for k = 2,6,10,14…, and 0 for odd k. This leads to the following Taylor series:
The function is similarly defined by requiring that
This leads to the Taylor series
Complex numbers
editThe natural numbers are used for counting. By subtracting natural numbers from natural numbers, we can create integers that are not natural numbers. By dividing integers by integers (other than zero) we can create rational numbers that are not integers. By taking the square roots of positive rational numbers we can create real numbers that are irrational. And by taking the square roots of negative numbers we can create complex numbers that are imaginary.
Any imaginary number is a real number multiplied by the positive square root of for which we have the symbol
Every complex number is the sum of a real number (the real part of ) and an imaginary number Somewhat confusingly, the imaginary part of is the real number
Because real numbers can be visualized as points on a line, they are also referred to as (or thought of as constituting) the real line. Because complex numbers can be visualized as points in a plane, they are also referred to as (or thought of as constituting) the complex plane. This plane contains two axes, one horizontal (the real axis constituted by the real numbers) and one vertical (the imaginary axis constituted by the imaginary numbers).
Do not be mislead by the whimsical tags "real" and "imaginary". No number is real in the sense in which, say, apples are real. The real numbers are no less imaginary in the ordinary sense than the imaginary numbers, and the imaginary numbers are no less real in the mathematical sense than the real numbers. If you are not yet familiar with complex numbers, it is because you don't need them for counting or measuring. You need them for calculating the probabilities of measurement outcomes.
This diagram illustrates, among other things, the addition of complex numbers:
As you can see, adding two complex numbers is done in the same way as adding two vectors and in a plane.
Instead of using rectangular coordinates specifying the real and imaginary parts of a complex number, we may use polar coordinates specifying the absolute value or modulus and the complex argument or phase , which is an angle measured in radians. Here is how these coordinates are related:
(Remember Pythagoras?)
All you need to know to be able to multiply complex numbers is that :
There is, however, an easier way to multiply complex numbers. Plugging the power series (or Taylor series) for and
into the expression and rearranging terms, we obtain
But this is the power/Taylor series for the exponential function with ! Hence Euler's formula
and this reduces multiplying two complex numbers to multiplying their absolute values and adding their phases:
An extremely useful definition is the complex conjugate of Among other things, it allows us to calculate the absolute square by calculating the product
1. Show that
2. Arguably the five most important numbers are Write down an equation containing each of these numbers just once. (Answer?)
Vectors (spatial)
editA vector is a quantity that has both a magnitude and a direction. Vectors can be visualized as arrows. The following figure shows what we mean by the components of a vector
The sum of two vectors has the components
- Explain the addition of vectors in terms of arrows.
The dot product of two vectors is the number
Its importance arises from the fact that it is invariant under rotations. To see this, we calculate
According to Pythagoras, the magnitude of is If we use a different coordinate system, the components of will be different: But if the new system of axes differs only by a rotation and/or translation of the axes, the magnitude of will remain the same:
The squared magnitudes and are invariant under rotations, and so, therefore, is the product
- Show that the dot product is also invariant under translations.
Since by a scalar we mean a number that is invariant under certain transformations (in this case rotations and/or translations of the coordinate axes), the dot product is also known as (a) scalar product. Let us prove that
where is the angle between and To do so, we pick a coordinate system in which In this coordinate system with Since is a scalar, and since scalars are invariant under rotations and translations, the result (which makes no reference to any particular frame) holds in all frames that are rotated and/or translated relative to
We now introduce the unit vectors whose directions are defined by the coordinate axes. They are said to form an orthonormal basis. Ortho because they are mutually orthogonal:
Normal because they are unit vectors:
And basis because every vector can be written as a linear combination of these three vectors — that is, a sum in which each basis vector appears once, multiplied by the corresponding component of (which may be 0):
It is readily seen that which is why we have that
Another definition that is useful (albeit only in a 3-dimensional space) is the cross product of two vectors:
- Show that the cross product is antisymmetric:
As a consequence,
- Show that
Thus is perpendicular to both and
- Show that the magnitude of equals where is the angle between and Hint: use a coordinate system in which and
Since is also the area of the parallelogram spanned by and we can think of as a vector of magnitude perpendicular to Since the cross product yields a vector, it is also known as vector product.
(We save ourselves the trouble of showing that the cross product is invariant under translations and rotations of the coordinate axes, as is required of a vector. Let us however note in passing that if and are polar vectors, then is an axial vector. Under a reflection (for instance, the inversion of a coordinate axis) an ordinary (or polar) vector is invariant, whereas an axial vector changes its sign.)
Here is a useful relation involving both scalar and vector products:
Fields
editAs you will remember, a function is a machine that accepts a number and returns a number. A field is a function that accepts the three coordinates of a point or the four coordinates of a spacetime point and returns a scalar, a vector, or a tensor (either of the spatial variety or of the 4-dimensional spacetime variety).
Gradient
editImagine a curve in 3-dimensional space. If we label the points of this curve by some parameter then can be represented by a 3-vector function We are interested in how much the value of a scalar field changes as we go from a point of to the point of By how much changes will depend on how much the coordinates of change, which are themselves functions of The changes in the coordinates are evidently given by
while the change in is a compound of three changes, one due to the change in one due to the change in and one due to the change in :
The first term tells us by how much changes as we go from to the second tells us by how much changes as we go from to and the third tells us by how much changes as we go from to
Shouldn't we add the changes in that occur as we go first from to then from to and then from to ? Let's calculate.
If we take the limit (as we mean to whenever we use ), the last term vanishes. Hence we may as well use in place of Plugging (*) into (**), we obtain
Think of the expression in brackets as the dot product of two vectors:
- the gradient of the scalar field which is a vector field with components
- the vector which is tangent on
If we think of as the time at which an object moving along is at then the magnitude of is this object's speed.
is a differential operator that accepts a function and returns its gradient
The gradient of is another input-output device: pop in and get the difference
The differential operator is also used in conjunction with the dot and cross products.
Curl
editThe curl of a vector field is defined by
To see what this definition is good for, let us calculate the integral over a closed curve (An integral over a curve is called a line integral, and if the curve is closed it is called a loop integral.) This integral is called the circulation of along (or around the surface enclosed by ). Let's start with the boundary of an infinitesimal rectangle with corners and

The contributions from the four sides are, respectively,
These add up to

Let us represent this infinitesimal rectangle of area (lying in the - plane) by a vector whose magnitude equals and which is perpendicular to the rectangle. (There are two possible directions. The right-hand rule illustrated on the right indicates how the direction of is related to the direction of circulation.) This allows us to write (***) as a scalar (product) Being a scalar, it it is invariant under rotations either of the coordinate axes or of the infinitesimal rectangle. Hence if we cover a surface with infinitesimal rectangles and add up their circulations, we get
Observe that the common sides of all neighboring rectangles are integrated over twice in opposite directions. Their contributions cancel out and only the contributions from the boundary of survive.
The bottom line:

This is Stokes' theorem. Note that the left-hand side depends solely on the boundary of So, therefore, does the right-hand side. The value of the surface integral of the curl of a vector field depends solely on the values of the vector field at the boundary of the surface integrated over.
If the vector field is the gradient of a scalar field and if is a curve from to then
The line integral of a gradient thus is the same for all curves having identical end points. If then is a loop and vanishes. By Stokes' theorem it follows that the curl of a gradient vanishes identically:
Divergence
editThe divergence of a vector field is defined by
To see what this definition is good for, consider an infinitesimal volume element with sides Let us calculate the net (outward) flux of a vector field through the surface of There are three pairs of opposite sides. The net flux through the surfaces perpendicular to the axis is
It is obvious what the net flux through the remaining surfaces will be. The net flux of out of thus equals
If we fill up a region with infinitesimal parallelepipeds and add up their net outward fluxes, we get Observe that the common sides of all neighboring parallelepipeds are integrated over twice with opposite signs — the flux out of one equals the flux into the other. Hence their contributions cancel out and only the contributions from the surface of survive. The bottom line:
This is Gauss' law. Note that the left-hand side depends solely on the boundary of So, therefore, does the right-hand side. The value of the volume integral of the divergence of a vector field depends solely on the values of the vector field at the boundary of the region integrated over.
If is a closed surface — and thus the boundary or a region of space — then itself has no boundary (symbolically, ). Combining Stokes' theorem with Gauss' law we have that
The left-hand side is an integral over the boundary of a boundary. But a boundary has no boundary! The boundary of a boundary is zero: It follows, in particular, that the right-hand side is zero. Thus not only the curl of a gradient but also the divergence of a curl vanishes identically:
Some useful identities
editThe ABCs of relativity
editSee also the Wikibook Special relativity that contains an in-depth text on this subject.
The principle of relativity
editIf we use an inertial system (a.k.a. inertial coordinate system, inertial frame of reference, or inertial reference frame), then the components of the position of any freely moving classical object ("point mass") change by equal amounts in equal time intervals Evidently, if is an inertial frame then so is a reference frame that is, relative to
- shifted ("translated") in space by any distance and/or in any direction,
- translated in time by any interval,
- rotated by any angle about any axis, and/or
- moving with any constant velocity.
The principle of relativity states that all inertial systems are "created equal": the laws of physics are the same as long as they are formulated with respect to an inertial frame — no matter which. (Describing the same physical event or state of affairs using different inertial systems is like saying the same thing in different languages.) The first three items tell us that one inertial frame is as good as any other frame as long as the other frame differs by a shift of the coordinate origin in space and/or time and/or by a rotation of the spatial coordinate axes. What matters in physics are relative positions (the positions of objects relative to each other), relative times (the times of events relative to each other), and relative orientations (the orientations of objects relative to each other), inasmuch as these are unaffected by translations in space and/or time and by rotations of the spatial axes. In the physical world, there are no absolute positions, absolute times, or absolute orientations.
The fourth item tells us, in addition, that one inertial frame is as good as any other frame as long as the two frames move with a constant velocity relative to each other. What matters are relative velocities (the velocities of objects relative to each other), inasmuch as these are unaffected by a coordinate boost — the switch from an inertial frame to a frame moving with a constant velocity relative to In the physical world, there are no absolute velocities and, in particular, there is no absolute rest.
It stands to reason. For one thing, positions are properties of objects, not things that exist even when they are not "occupied" or possessed. For another, the positions of objects are defined relative to the positions of other objects. In a universe containing a single object, there is no position that one could attribute to that object. By the same token, all physically meaningful times are the times of physical events, and they too are relatively defined, as the times between events. In a universe containing a single event, there is not time that one could attribute to that event. But if positions and times are relatively defined, then so are velocities.
That there is no such thing as absolute rest has not always been as obvious as it should have been. Two ideas were responsible for the erroneous notion that there is a special class of inertial frames defining "rest" in an absolute sense: the idea that electromagnetic effects are transmitted by waves, and the idea that these waves require a physical medium (dubbed "ether") for their propagation. If there were such a medium, one could define absolute rest as equivalent to being at rest with respect to it.
Lorentz transformations (general form)
editWe want to express the coordinates and of an inertial frame in terms of the coordinates and of another inertial frame We will assume that the two frames meet the following conditions:
- their spacetime coordinate origins coincide ( mark the same spacetime location as ),
- their space axes are parallel, and
- moves with a constant velocity relative to
What we know at this point is that whatever moves with a constant velocity in will do so in It follows that the transformation maps straight lines in onto straight lines in Coordinate lines of in particular, will be mapped onto straight lines in This tells us that the dashed coordinates are linear combinations of the undashed ones,
We also know that the transformation from to can only depend on so and are functions of Our task is to find these functions. The real-valued functions and actually can depend only on so and A vector function depending only on must be parallel (or antiparallel) to and its magnitude must be a function of We can therefore write and (It will become clear in a moment why the factor is included in the definition of ) So,
Let's set equal to This implies that As we are looking at the trajectory of an object at rest in must be constant. Hence,
Let's write down the inverse transformation. Since moves with velocity relative to it is
To make life easier for us, we now chose the space axes so that Then the above two (mutually inverse) transformations simplify to
Plugging the first transformation into the second, we obtain
The first of these equations tells us that
- and
The second tells us that
- and
Combining with (and taking into account that ), we obtain
Using to eliminate we obtain and
Since the first of the last two equations implies that we gather from the second that
tells us that must, in fact, be equal to 1, since we have assumed that the space axes of the two frames a parallel (rather than antiparallel).
With and yields Upon solving for we are left with expressions for and depending solely on :
Quite an improvement!
To find the remaining function we consider a third inertial frame which moves with velocity relative to Combining the transformation from to
with the transformation from to
we obtain the transformation from to :
The direct transformation from to must have the same form as the transformations from to and from to , namely
where is the speed of relative to Comparison of the coefficients marked with stars yields two expressions for which of course must be equal:
It follows that and this tells us that
is a universal constant. Solving the first equality for we obtain
This allows us to cast the transformation
into the form
Trumpets, please! We have managed to reduce five unknown functions to a single constant.
Composition of velocities
editIn fact, there are only three physically distinct possibilities. (If the magnitude of depends on the choice of units, and this tells us something about us rather than anything about the physical world.)
The possibility yields the Galilean transformations of Newtonian ("non-relativistic") mechanics:
(The common practice of calling theories with this transformation law "non-relativistic" is inappropriate, inasmuch as they too satisfy the principle of relativity.) In the remainder of this section we assume that
Suppose that object moves with speed relative to object and that this moves with speed relative to object If and move in the same direction, what is the speed of relative to ? In the previous section we found that
and that
This allows us to write
Expressing in terms of and the respective velocities, we obtain
which implies that
We massage this into
divide by and end up with:
Thus, unless we don't get the speed of relative to by simply adding the speed of relative to to the speed of relative to .
Proper time
editConsider an infinitesimal segment of a spacetime path In it has the components in it has the components Using the Lorentz transformation in its general form,
it is readily shown that
We conclude that the expression
is invariant under this transformation. It is also invariant under rotations of the spatial axes (why?) and translations of the spacetime coordinate origin. This makes a 4-scalar.
What is the physical significance of ?
A clock that travels along is at rest in any frame in which lacks spatial components. In such a frame, Hence is the time it takes to travel along as measured by a clock that travels along is the proper time (or proper duration) of The proper time (or proper duration) of a finite spacetime path accordingly, is
An invariant speed
editIf then there is a universal constant with the dimension of a velocity, and we can cast into the form
If we plug in then instead of the Galilean we have More intriguingly, if object moves with speed relative to and if moves with speed relative to then moves with the same speed relative to : The speed of light thus is an invariant speed: whatever travels with it in one inertial frame, travels with the same speed in every inertial frame.
Starting from
we arrive at the same conclusion: if travels with relative to then it travels the distance in the time Therefore But then and this implies It follows that travels with the same speed relative to
An invariant speed also exists if but in this case it is infinite: whatever travels with infinite speed in one inertial frame — it takes no time to get from one place to another — does so in every inertial frame.
The existence of an invariant speed prevents objects from making U-turns in spacetime. If it obviously takes an infinite amount of energy to reach Since an infinite amount of energy isn't at our disposal, we cannot start vertically in a spacetime diagram and then make a U-turn (that is, we cannot reach, let alone "exceed", a horizontal slope. ("Exceeding" a horizontal slope here means changing from a positive to a negative slope, or from going forward to going backward in time.)
If it takes an infinite amount of energy to reach even the finite speed of light. Imagine you spent a finite amount of fuel accelerating from 0 to In the frame in which you are now at rest, your speed is not a whit closer to the speed of light. And this remains true no matter how many times you repeat the procedure. Thus no finite amount of energy can make you reach, let alone "exceed", a slope equal to ("Exceeding" a slope equal to means attaining a smaller slope. As we will see, if we were to travel faster than light in any one frame, then there would be frames in which we travel backward in time.)
The case against
editIn a hypothetical world with we can define (a universal constant with the dimension of a velocity), and we can cast into the form
If we plug in then instead of the Galilean we have Worse, if we plug in we obtain : if object travels with speed relative to and if travels with speed relative to (in the same direction), then travels with an infinite speed relative to ! And if travels with relative to and travels with relative to 's speed relative to is negative:
If we use units in which then the invariant proper time associated with an infinitesimal path segment is related to the segment's inertial components via
This is the 4-dimensional version of the 3-scalar which is invariant under rotations in space. Hence if is positive, the transformations between inertial systems are rotations in spacetime. I guess you now see why in this hypothetical world the composition of two positive speeds can be a negative speed.
Let us confirm this conclusion by deriving the composition theorem (for ) from the assumption that the and axes are rotated relative to the and axes.
The speed of an object following the dotted line is relative to the speed of relative to is and the speed of relative to is Invoking the trigonometric relation
we conclude that Solving for we obtain
How can we rule out the a priori possibility that ? As shown in the body of the book, the stability of matter — to be precise, the existence of stable objects that (i) have spatial extent (they "occupy" space) and (ii) are composed of a finite number of objects that lack spatial extent (they don't "occupy" space) — rests on the existence of relative positions that are (a) more or less fuzzy and (b) independent of time. Such relative positions are described by probability distributions that are (a) inhomogeneous in space and (b) homogeneous in time. Their objective existence thus requires an objective difference between spactime's temporal dimension and its spatial dimensions. This rules out the possibility that
How? If and if we use natural units, in which we have that
As far as physics is concerned, the difference between the positive sign in front of and the negative signs in front of and is the only objective difference between time and the spatial dimensions of spacetime. If were positive, not even this difference would exist.
The case against zero K
editAnd what argues against the possibility that ?
Recall the propagator for a free and stable particle:
If were to vanish, we would have There would be no difference between inertial time and proper time, and every spacetime path leading from to would contribute the same amplitude to the propagator which would be hopelessly divergent as a result. Worse, would be independent of the distance between and To obtain well-defined, finite probabilities, cancellations ("destructive interference") must occur, and this rules out that
The actual Lorentz transformations
editIn the real world, therefore, the Lorentz transformations take the form
Let's explore them diagrammatically, using natural units (). Setting we have This tells us that the slope of the axis relative to the undashed frame is Setting we have This tells us that the slope of the axis is The dashed axes are thus rotated by the same angle in opposite directions; if the axis is rotated clockwise relative to the axis, then the axis is rotated counterclockwise relative to the axis.
We arrive at the same conclusion if we think about the synchronization of clocks in motion. Consider three clocks (1,2,3) that travel with the same speed relative to To synchronize them, we must send signals from one clock to another. What kind of signals? If we want our synchronization procedure to be independent of the language we use (that is, independent of the reference frame), then we must use signals that travel with the invariant speed
Here is how it's done:
Light signals are sent from clock 2 (event ) and are reflected by clocks 1 and 3 (events and respectively). The distances between the clocks are adjusted so that the reflected signals arrive simultaneously at clock 2 (event ). This ensures that the distance between clocks 1 and 2 equals the distance between clocks 2 and 3, regardless of the inertial frame in which they are compared. In where the clocks are at rest, the signals from have traveled equal distances when they reach the first and the third clock, respectively. Since they also have traveled with the same speed they have traveled for equal times. Therefore the clocks must be synchronized so that and are simultaneous. We may use the worldline of clock 1 as the axis and the straight line through and as the axis. It is readily seen that the three angles in the above diagram are equal. From this and the fact that the slope of the signal from to equals 1 (given that ), the equality of the two angles follows.
Simultaneity thus depends on the language — the inertial frame — that we use to describe a physical situation. If two events are simultaneous in one frame, then there are frames in which happens after as well as frames in which hapens before
Where do we place the unit points on the space and time axes? The unit point of the time axis of has the coordinates and satisfies as we gather from the version of (\ref{ds2}). The unit point of the axis has the coordinates and satisfies The loci of the unit points of the space and time axes are the hyperbolas that are defined by these equations:
Lorentz contraction, time dilatation
editImagine a meter stick at rest in At the time its ends are situated at the points and At the time they are situated at the points and which are less than a meter apart. Now imagine a stick (not a meter stick) at rest in whose end points at the time are O and C. In they are a meter apart, but in the stick's rest-frame they are at and and thus more than a meter apart. The bottom line: a moving object is contracted (shortened) in the direction in which it is moving.
Next imagine two clocks, one () at rest in and located at and one () at rest in and located at At indicates that one second has passed, while at (which in is simultaneous with ), indicates that more than a second has passed. On the other hand, at (which in is simultaneous with ), indicates that less than a second has passed. The bottom line: a moving clock runs slower than a clock at rest.
Example: Muons ( particles) are created near the top of the atmosphere, some ten kilometers up, when high-energy particles of cosmic origin hit the atmosphere. Since muons decay spontaneously after an average lifetime of 2.2 microseconds, they don't travel much farther than 600 meters. Yet many are found at sea level. How do they get that far?
The answer lies in the fact that most of them travel at close to the speed of light. While from its own point of view (that is, relative to the inertial system in which it is at rest), a muon only lives for about 2 microseconds, from our point of view (that is, relative to an inertial system in which it travels close to the speed of light), it lives much longer and has enough time to reach the Earth's surface.
4-vectors
edit3-vectors are triplets of real numbers that transform under rotations like the coordinates 4-vectors are quadruplets of real numbers that transform under Lorentz transformations like the coordinates of
You will remember that the scalar product of two 3-vectors is invariant under rotations of the (spatial) coordinate axes; after all, this is why we call it a scalar. Similarly, the scalar product of two 4-vectors and defined by
is invariant under Lorentz transformations (as well as translations of the coordinate origin and rotations of the spatial axes). To demonstrate this, we consider the sum of two 4-vectors and calculate
The products and are invariant 4-scalars. But if they are invariant under Lorentz transformations, then so is the scalar product
One important 4-vector, apart from is the 4-velocity which is tangent on the worldline is a 4-vector because is one and because is a scalar (to be precise, a 4-scalar).
The norm or "magnitude" of a 4-vector is defined as It is readily shown that the norm of equals (exercise!).
Thus if we use natural units, the 4-velocity is a unit vector.





























































![{\displaystyle V=-\int _{r}^{\infty }F(r')\,dr'=-\int _{r}^{\infty }\!{e^{2} \over (r')^{2}}\,dr'=+\left[{e^{2} \over r'}\right]_{r}^{\infty }=0-{e^{2} \over r}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/993b559a3ec2ac0420e5b42df9a7dd06d76091db)








































































![{\displaystyle \psi (x,t)={1 \over {\sqrt {2\pi }}}\int {\overline {\psi }}(k)\,e^{i[kx-\omega (k)t]}dk={1 \over {\sqrt {2\pi }}}\int {\overline {\psi }}(k,t)\,e^{ikx}dk}](https://wikimedia.org/api/rest_v1/media/math/render/svg/decd70ac0746010d4114e8be9a3aff7f4567684f)
























![{\displaystyle \langle k\rangle =\int \!\int {\overline {\psi }}\,^{*}(k')\,k\,{\overline {\psi }}(k)\left[{\frac {1}{2\pi }}\int e^{i(k-k')x}dx\right]dk\,dk'.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eeb26219d324cc48516a301db11ad6b4a291924a)

















![{\displaystyle \psi _{k'}(x,t)={\frac {1}{\sqrt {2\pi }}}\int \delta (k-k')\,e^{i[kx-\omega (k)t]}dk={\frac {1}{\sqrt {2\pi }}}\,e^{i[k'x-\omega (k')t]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0e7b1621aa59368c5ba766dba1d06cb884be467)




























![{\displaystyle |\langle D|L\rangle +\langle D|R\rangle |^{2}=1/d^{2}(DL)+1/d^{2}(DR)+2\cos(k\Delta )/[d(DL)\,d(DR)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d9ae74f81ec3d5ec56339702289b5d7197b7333)






















![{\displaystyle Z[{\mathcal {C}}:A\rightarrow B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1ef35fbc891d20f93d3040cf1b066d1537908e)
![{\displaystyle \langle B|A\rangle =\int \!{\mathcal {DC}}\,Z[{\mathcal {C}}:A\rightarrow B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/560ba2e4f536aae1082a145b86cd3272a3d60266)




![{\displaystyle Z[{\mathcal {C}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12cec7ed6cd140471a1dc9f9eb7d134157496870)












![{\displaystyle Z[{\mathcal {C}}]=e^{z\,s[{\mathcal {C}}:A\rightarrow B]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cda021a17ce0b0d0dab056edb00df34b3126dea7)
![{\displaystyle s[{\mathcal {C}}:A\rightarrow B]=\int _{\mathcal {C}}ds}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d39c96010ad1834d2b77e7fda2eedc55306354e0)





![{\displaystyle \int \!d^{3}r_{B}\left|\langle t_{B},\mathbf {r} _{B}|t_{A},\mathbf {r} _{A}\rangle \right|^{2}=\int \!d^{3}r_{B}\left|\int \!{\mathcal {DC}}\,e^{z\,s[{\mathcal {C}}:A\rightarrow B]}\right|^{2}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38f718f7da7c6d4d05653a32285c6728865345d9)





![{\displaystyle e^{a\,s[{\mathcal {C}}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4790d4570e8238f60dac01995dbe582f124954ec)





![{\displaystyle Z=e^{-ib\,s[{\mathcal {C}}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76a7995ac71573a7048cc185d9fb70ee9115d848)

![{\displaystyle Z=e^{-i\,2\pi \,b\,s[{\mathcal {C}}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e44157da1908243e02585b691660c746393b59f)

![{\displaystyle Z=e^{-i(2\pi /h)\,b\,s[{\mathcal {C}}]}=e^{-(i/\hbar )\,b\,s[{\mathcal {C}}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf41d385d7f74dd942da6bbb24779eacc88c2178)

![{\displaystyle Z=e^{-(i/\hbar )\,b\,c^{2}\,s[{\mathcal {C}}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5eca1b6ac00d70dbcb1c12dc4a7f29c4ae4fa48)

![{\displaystyle \langle B|A\rangle =\int \!{\mathcal {DC}}\,Z[{\mathcal {C}}:A\rightarrow B].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72eaf6dfa02f89e76d82984dd9eb38306e5b832f)
![{\displaystyle Z[{\mathcal {C}}]=e^{-(i/\hbar )\,m\,c^{2}\,s[{\mathcal {C}}]},\qquad s[{\mathcal {C}}]=\int _{\mathcal {C}}ds,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95777a5c221f93c1702f67750fd8cd2887d0838f)




![{\displaystyle Z[{\mathcal {C}}]=e^{(i/\hbar )\,S[{\mathcal {C}}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0c875d7b6098a105324faf2a00b5d492b73ddea)
![{\displaystyle S[{\mathcal {C}}]=\int _{\mathcal {C}}dS}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df35908de191c7e92ca25dd1ac7afe737a775617)
![{\displaystyle S[{\mathcal {C}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32185fe1ae3e35a7a07a246a1571f3f1d9218e1b)
![{\displaystyle s[{\mathcal {C}}]=\int _{\mathcal {C}}ds}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a41ecbcaeb2ff781301fedda92d148da0b198b96)

![{\displaystyle dS[d{\mathcal {C}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d12fd58c96db2b6188be62642138c0bbb09b3dec)
![{\displaystyle S[{\mathcal {C}}]=-m\,c^{2}\,s[{\mathcal {C}}],\qquad dS[d{\mathcal {C}}]=-m\,c^{2}\,ds.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef2d4b6235f56a34782cd011b4a96c669b48d85e)
























![{\displaystyle S[{\mathcal {C}}]\rightarrow S[{\mathcal {C}}']\neq S[{\mathcal {C}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e34648686e9d15561f525608c2003aafcde37199)




![{\displaystyle (^{*})\quad \int _{{\mathcal {C}}'}dS-\int _{\mathcal {C}}dS=\int _{\mathcal {C}}\left[{\partial dS \over \partial t}\delta t+{\partial dS \over \partial \mathbf {r} }\cdot \delta \mathbf {r} +{\partial dS \over \partial dt}d\,\delta t+{\partial dS \over \partial d\mathbf {r} }\cdot d\,\delta \mathbf {r} \right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd986655174c40d198342caff54ab5c9bf73c1fe)


![{\displaystyle \delta S=\int \left[\left({\partial dS \over \partial t}-d{\partial dS \over \partial dt}\right)\delta t+\left({\partial dS \over \partial \mathbf {r} }-d{\partial dS \over \partial d\mathbf {r} }\right)\cdot \delta \mathbf {r} \right]+\int d\left({\partial dS \over \partial dt}\delta t+{\partial dS \over \partial d\mathbf {r} }\cdot \delta \mathbf {r} \right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/175529713e04b4e19b6654372ba39f6d49c2a479)








![{\displaystyle I({\mathcal {T}})=\int _{\mathcal {T}}{\mathcal {DC}}e^{(i/\hbar )S[{\mathcal {C}}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/989c386d3a3d3376ba4f0a0c54f6bc69df72401a)

![{\displaystyle S[{\mathcal {C}}]/\hbar }](https://wikimedia.org/api/rest_v1/media/math/render/svg/50c6f20852d1372c22ae636a5bb02793f3d01b3c)



![{\displaystyle e^{(i/\hbar )S[{\mathcal {C}}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/909f56511c1d7741e6170a851f6898921161a865)
![{\displaystyle [0,2\pi ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/931e83eeed5210f609d30d88d4b3e751ffcf8c92)
![{\displaystyle S[{\mathcal {C}}]/\hbar \rightarrow \infty ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61ee5c40ee9ff21b48b00ccf04da6ddf5ea7e7cd)

![{\displaystyle S[{\mathcal {C}}]/\hbar \rightarrow \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/42a51e1a66c64bee8906ce97bf007e5f309c484c)

![{\displaystyle S[{\mathcal {C}}]=-m\,c^{2}\,s[{\mathcal {C}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6847833d8a7b95a87d6688209e396acccb099f77)
![{\displaystyle |-m\,c^{2}\,s[{\mathcal {C}}]|,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c43cab49dcd11a14e34b763de9dbabfa04292e9e)


![{\displaystyle \langle {\mathcal {P}}_{f},t_{f}|{\mathcal {P}}_{i},t_{i}\rangle =\int \!{\mathcal {DC}}\,e^{(i/\hbar )S[{\mathcal {C}}]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb7cf16b6d2cd4896968e978d85d443e35ea1bfb)
















![{\displaystyle S[{\mathcal {C}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80eac925d584f2615b6b2afd95347ffbb19a3e47)
![{\displaystyle S[{\mathcal {C}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a2cab2aff5c3318bf5f323603acbe275c4035e2)





























![{\displaystyle dS=-(E_{k}+qV)\,dt+[\mathbf {p} _{k}+(q/c)\mathbf {A} ]\cdot d\mathbf {r} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/76d24186c4bede17212148c2fa641fdb8150f164)





![{\displaystyle d\mathbf {p} _{k}+{q \over c}d\mathbf {A} =d\mathbf {p} _{k}+{q \over c}\left[dt{\partial \mathbf {A} \over \partial t}+\left(d\mathbf {r} \cdot {\partial \over \partial \mathbf {r} }\right)\mathbf {A} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3371cba964aa53e1f1dec5226bb823c0558f0629)
![{\displaystyle -q{\partial V \over \partial \mathbf {r} }dt+{q \over c}{\partial (\mathbf {A} \cdot d\mathbf {r} ) \over \partial \mathbf {r} }=-q{\partial V \over \partial \mathbf {r} }dt+{q \over c}\left[\left(d\mathbf {r} \cdot {\partial \over \partial \mathbf {r} }\right)\mathbf {A} +d\mathbf {r} \times \left({\partial \over \partial \mathbf {r} }\times \mathbf {A} \right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6151b8f186d369cb0d68585b16e2f80181311f90)















![{\displaystyle \quad =-V(dt/2,0,0,0)\,dt+\left[A_{x}(0,dx/2,0,0)+{\partial A_{x} \over \partial t}dt\right]dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a951a567645f5eb4bbdd5a7ea337eaac53926ecf)


![{\displaystyle =A_{x}(0,dx/2,0,0)\,dx-\left[V(dt/2,0,0,0)+{\partial V \over \partial x}dx\right]dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9d37cd2d7410184894e1b32ff9be38968a7fe78)






![{\displaystyle =A_{z}(0,0,0,dz/2)\,dz+\left[A_{y}(0,0,dy/2,0)+{\partial A_{y} \over \partial z}dz\right]dy,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bf1b951a7d6ab779c6c262758f4f922bb2c9677)

![{\displaystyle =A_{y}(0,0,dy/2,0)\,dy+\left[A_{z}(0,0,0,dz/2)+{\partial A_{z} \over \partial y}dy\right]dz,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf5146def106e98da62a252b30699f3824d18045)















![{\displaystyle q\,[-V+\mathbf {A} (t,\mathbf {r} )\cdot (\mathbf {v} /c)]\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20e8b24d546fe887ebe07274865fbd8c475ab464)

![{\displaystyle S[{\mathcal {C}}]=-mc^{2}(t_{B}-t_{A})+\int _{\mathcal {C}}dt\left[{\textstyle {m \over 2}}v^{2}-V(t,\mathbf {r} )\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4499cc5df31a2145f1587b9f3fcb45f903aa2f7)
![{\displaystyle \langle B|A\rangle =\int {\mathcal {DC}}e^{(i/\hbar )\int _{\mathcal {C}}dt[(m/2)v^{2}-V]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10b995d212329a44f0dfdd682f340c4fcc14237f)



























![{\displaystyle \left[1-{i\epsilon \over \hbar }V(t,x)\right]\left[\psi (t,x)+{\partial \psi \over \partial x}\eta +{\frac {1}{2}}{\partial ^{2}\psi \over \partial x^{2}}\eta ^{2}\right]=\left[1-{i\epsilon \over \hbar }V(t,x)\right]\!\psi (t,x)+{\partial \psi \over \partial x}\eta +{\partial ^{2}\psi \over \partial x^{2}}{\eta ^{2} \over 2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3b2d776e71c82d9145f8fca7963e4ce1a3c639c)
























![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)


![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)

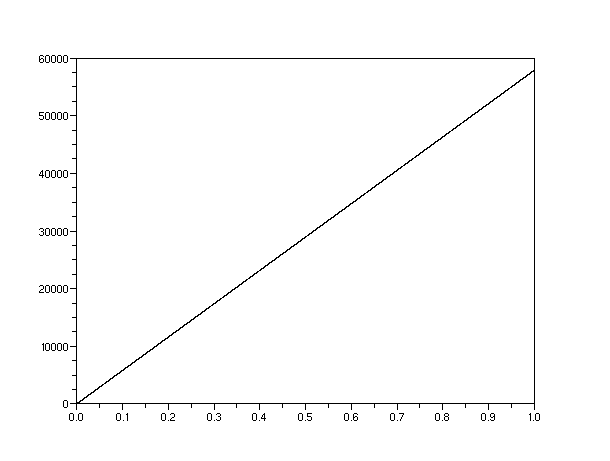












![{\displaystyle {d^{2}\psi (x) \over dx^{2}}=A(x)\,\psi (x),\qquad A(x)={2m \over \hbar ^{2}}{\Big [}V(x)-E{\Big ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19e4728d3b49118d58dd0fde955cd01b39fa1fde)







































































































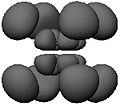














































![{\displaystyle e^{i\alpha (2\tau )}=[e^{i\alpha (\tau )}]^{2}=e^{i2\alpha (\tau )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d3497e883347d422569ad59360c95ff610dc075)












![{\displaystyle e^{i\beta (2\kappa )}=[e^{i\beta (\kappa )}]^{2}=e^{i2\beta (\kappa )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61ce647884ef73ddb7bae9e5ad29c8609421dc33)






















![{\displaystyle [{\hat {A}},{\hat {B}}]\equiv {\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae9cc9448b540b49dcc4a3f14c07d358ad4fbbda)


![{\displaystyle [{\hat {l}}_{x},{\hat {l}}_{y}]\,=i\hbar {\hat {l}}_{z}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06a5996c186acf298548a8472f13d4ec66bb36b4)
![{\displaystyle [{\hat {l}}_{y},{\hat {l}}_{z}]=i\hbar {\hat {l}}_{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf21bcf6e7d03daf67d00262f75a31dfbabef32a)
![{\displaystyle [{\hat {l}}_{z},{\hat {l}}_{x}]=i\hbar {\hat {l}}_{y}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6782b9785c3c1fdbe653926e270b99abdc1cf4d6)




![{\displaystyle E\,{\partial \psi \over \partial t}=-{\hbar ^{2} \over 2m}\left[{\partial ^{2}\psi \over \partial x_{1}^{2}}+{\partial ^{2}\psi \over \partial y_{1}^{2}}+{\partial ^{2}\psi \over \partial z_{1}^{2}}+{\partial ^{2}\psi \over \partial x_{2}^{2}}+{\partial ^{2}\psi \over \partial y_{2}^{2}}+{\partial ^{2}\psi \over \partial z_{2}^{2}}\right]+\left[-{\frac {2e^{2}}{r_{1}}}-{\frac {2e^{2}}{r_{2}}}+{\frac {e^{2}}{r_{12}}}\right]\psi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dd92e27f87af401228ecea495f7bc29e4657a1d)
























![{\displaystyle {\frac {\partial \rho }{\partial t}}=-{\frac {i}{\hbar }}\psi ^{*}\left[{\frac {1}{2m}}\left({\frac {\hbar }{i}}{\frac {\partial }{\partial \mathbf {r} }}-\mathbf {A} \right)\cdot \left({\frac {\hbar }{i}}{\frac {\partial }{\partial \mathbf {r} }}-\mathbf {A} \right)\psi +V\psi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d23fdabbde0cdbdb661a59e5da9d9e6383413680)
![{\displaystyle +{\frac {i}{\hbar }}\psi \left[{\frac {1}{2m}}\left(i\hbar {\frac {\partial }{\partial \mathbf {r} }}-\mathbf {A} \right)\cdot \left(i\hbar {\frac {\partial }{\partial \mathbf {r} }}-\mathbf {A} \right)\psi ^{*}+V\psi ^{*}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98727a8a7448922f0b5f337839182910d485ccd8)
![{\displaystyle {\frac {\partial \rho }{\partial t}}=-{\frac {i}{2m\hbar }}\left[\psi ^{*}\left(i\hbar {\frac {\partial }{\partial \mathbf {r} }}+\mathbf {A} \right)\cdot \left(i\hbar {\frac {\partial }{\partial \mathbf {r} }}+\mathbf {A} \right)\psi -\psi \left(i\hbar {\frac {\partial }{\partial \mathbf {r} }}-\mathbf {A} \right)\cdot \left(i\hbar {\frac {\partial }{\partial \mathbf {r} }}-\mathbf {A} \right)\psi ^{*}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb63f2ee8fad5069e8ef2da029a0eeb8e925ce34)






























![{\displaystyle [N(1)+N(6)]/N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1215e2f1ee97059fe7490164635d376217e970)

















































































































































![{\displaystyle f^{(n)}(0)=[f'(0)]^{n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4738a6202551698414ca14ef0093ba18de9114cd)













![{\displaystyle \exp[\ln(x)]=\ln[\exp(x)]=x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be6623b1f6e056d212af385326b1448a56ddaadc)

![{\displaystyle \exp\{\ln[f(x)]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dee3e2444ba3dc43d08180474133c155127c571b)


































































































































![{\displaystyle {\frac {\partial f(x{+}dx,y,z)}{\partial y}}={\frac {\partial \left[f(x,y,z)+{\frac {\partial f}{\partial x}}dx\right]}{\partial y}}={\frac {\partial f(x,y,z)}{\partial y}}+{\frac {\partial ^{2}f}{\partial y\,\partial x}}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da910b2b5f7b62c89ea28b6b4e94d9e6dab94322)





















![{\displaystyle {\overline {BC}}:\quad A_{z}(0,dy,dz/2)\,dz=\left[A_{z}(0,0,dz/2)+{\frac {\partial A_{z}}{\partial y}}dy\right]dz,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a791cb77c31fe3c62c684be02e769d777eb14b82)
![{\displaystyle {\overline {CD}}:\quad -A_{y}(0,dy/2,dz)\,dy=-\left[A_{y}(0,dy/2,0)+{\frac {\partial A_{y}}{\partial z}}dz\right]dy,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d68399d3570c7512370ce35f8249a6f2688371b)

![{\displaystyle (^{*}{}^{*}{}^{*})\quad \left[{\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right]dy\,dz=({\hbox{curl}}\,\mathbf {A} )_{x}\,dy\,dz.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/350effae9c88e937605059b807b049006ddb4e0e)
















![{\displaystyle \left[{\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\right]\,dx\,dy\,dz={\hbox{div}}\,\mathbf {A} \,d^{3}r.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a4a784f7f51bed471c20c62dc1670b71949e9c4)

































![{\displaystyle \mathbf {D} =[d(w)/w^{2}]\mathbf {w} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa802a1058978d8935aaa7cad208a913134cf22b)










































![{\displaystyle t''=a(v)\left[a(w)\,t+{1-a^{2}(w) \over a(w)\,w}x\right]+{1-a^{2}(v) \over a(v)\,v}{\Bigl [}a(w)\,x-a(w)\,wt{\Bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aac5ef850e58cf4313f158ff823495cfda63278d)
![{\displaystyle =\underbrace {\left[a(v)\,a(w)-{1-a^{2}(v) \over a(v)\,v}a(w)\,w\right]} _{\textstyle \star }t+{\Bigl [}\dots {\Bigr ]}\,x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f598d3a652be5ce24fbf91ac01439a8d4772177d)
![{\displaystyle x''=a(v){\Bigl [}a(w)\,x-a(w)\,wt{\Bigr ]}-a(v)\,v\left[a(w)\,t+{1-a^{2}(w) \over a(w)\,w}x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d163387fa694115abbe60fb231559ed50fe5046)
![{\displaystyle =\underbrace {\left[a(v)\,a(w)-a(v)\,v{1-a^{2}(w) \over a(w)\,w}\right]} _{\textstyle \star \,\star }x-{\Bigl [}\dots {\Bigr ]}\,t.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae3bd80d12d1822ff47c0e945207167ce442828d)



![{\displaystyle {\bigl [}1-a^{2}(v){\bigr ]}\,a^{2}(w)w^{2}={\bigl [}1-a^{2}(w){\bigr ]}\,a^{2}(v)v^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0284ddcbcc0b4d7c8d9e3d041abb9cec2496672a)







































































![{\displaystyle \langle B|A\rangle =\int {\mathcal {DC}}e^{-ibs[{\mathcal {C}}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/876f21d020e1dee53f4cf7c6bb67a504f1c08fc3)