Strength of Materials/Unsorted topics

Compatibility Conditions

In an Engineering Mechanics course, we use force equilibrium to solve for forces in individual members. However, there were cases where it was not possible and such problems were considered statically indeterminate problems. They require some constitutive equations to solve completely, and Hooke's law is such an equation.

For instance, consider a column fixed at both ends, and a load P applied at the center. Now, we know that reaction forces R₁ and R₂ act at either ends. Further, using force equilibrium, we have R₁ + R₂ = P. Here we have two unknowns, R₁ and R₂, but only one equation. We can apply Hooke's law, with displacements Δ₁ and Δ₂, where Δ₁ = R₁L/2AE and Δ₂ = R₂L/2AE. The second equation is Δ₁ = Δ₂, since the supports are fixed. Thus, we can solve the problem.

Finite Element Method

Consider a rod with different cross sections A_i and lengths L_i, so that each section has an equivalent spring constant of A_iE/L_i. If the forces at each node (where the area changes) are F_i, then we can write equations in terms of displacements of each node and the spring constant of each section for the force F_i. If the beam is fixed at both ends, then the forces can only act on the other nodes.

In the general case, if you have loads being applied to connected thin rods, you can use this method to solve for forces and deformations. The whole structure can be discretized, and the nodes numbered so that we get the matrix [k_ij].

This procedure of breaking down a complicated problem into a large number of simple ones is called the Finite Element Method.

The individual pieces are called elements, and in the above case we have used the line element. For a general 2-D problem, we would need to use triangular elements at least. The matrix for a typical problem will contain hundreds of such elements and the size of the matrix be same as the number of elements. However, as most of the members are zero, the matrix is called a sparse matrix, and it can be solved much faster than the typical matrix you would encounter, say, in a mathematics course.

Saint-Venant's Principle

So far we have been dealing with point loads acting at the ends of beams. We have assumed that the stress is the same as σ_av = P/A. However, this is not true close to the point of application of the load. Saint-Venant's principle (by the French elastician Saint-Venant) states that the stresses remote from the point of application of the load are not affected by the precise behaviour of the structure close to the point of application of the load. In the drawing shown, this means that although the stress field at A-A might be hard to calculate, at B-B the stress can be approximated as P/A. S-V's principle is consistent with many years of experiment and analysis, but has not been proven.

Stress Concentration Factors

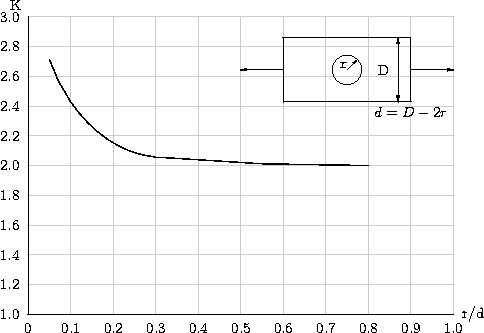
So far we have assumed that the stress at all points in a cross section is the same, and by and large that is correct. However, there is an increase in stress near the point loads and discontinuities. The peak loads are a function of the average stress calculated by methods stated previously. The correct peak loads can only be obtained by methods like finite element analysis. However, charts have been published for several typical scenarios. As mentioned earlier, the peak stresses σ_p is a function of the average stress σ_av. Now, we have σ_p = K×σ_av, where K is called the stress concentration factor and can be looked up from tables for common scenarios. The study of stress concentration factors is also a design guideline, and indicates the types of features that you should avoid in a real world situation. For instance, the stress concentration factor for a fillet radius increases rapidly beyond r < 0.1 d, so you should specify large fillet radii for your shafts or eliminate the change in diameter.

The above schematic shows the possible values of the stress concentration ratios K for a plate with a hole in it. The stress at the narrowest section is calculated based on d = D − 2r, where r is the radius of the hole and D is the width of the slab. As can be seen, the stress concentration is not significant till about r/d = 0.3.

Note that local stresses might not be as high as that implied by the stress concentration factors due to plastic flow of the material, since the stress concentration analysis is done for elastic flow.

Generalized Hooke's Law

Poisson's ratio shows the amount of change in dimension that occurs in another direction when a certain change occurs in one direction. The strain in each direction is the superposition of all the strains--the direct strains and the ones due to Poisson's ratio. We can therefore state the generalized Hooke's law as follows:

$\epsilon _{x}={\sigma _{x} \over E}-{\nu \sigma _{y} \over E}-{\nu \sigma _{z} \over E}$

$\epsilon _{y}={\nu \sigma _{x} \over E}-{\sigma _{y} \over E}-{\nu \sigma _{z} \over E}$

$\epsilon _{z}={\nu \sigma _{x} \over E}-{\nu \sigma _{y} \over E}-{\sigma _{z} \over E}$

$\gamma _{xy}={\tau _{xy} \over G}$

$\gamma _{yz}={\tau _{yz} \over G}$

$\gamma _{zx}={\tau _{zx} \over G}$

Note that these equations apply only to isotropic materials (steel, aluminum, copper, etc.) whose elastic properties are identical in all directions.

Relationships Between Moduli

Consider an element which has stresses σ₁ and σ₂ acting on it along the x and y directions respectively. Now consider further that σ₁ = σ and σ₂ = −σ.

The shear modulus can be expressed in terms of the Young's modulus:

$G={\frac {E}{2\left(1+\nu \right)}}$

Consider a body undergoing compression, so that the strains are ε_x, ε_y, and ε_z respectively. The fractional change in volume is thus ε_x + ε_y + ε_z. Applying the generalized version of Hooke's law, we have, the bulk modulus k is given by

$k={\frac {E}{3\left(1-2\nu \right)}}$

Pressure Vessels

Vessels, tanks, and pipelines that carry, store or receive fluids, at a pressure different than its surroundings, are called pressure vessels. Pressure vessels usually are thin walled structures containing fluids at high pressure. The design decision is to find the value for the thickness t of the pressure vessel for a given maximum pressure p. Since the thickness is much smaller than the radius of the vessel r, the inner and outer radius are taken to be equal. For the longitudinal direction, we have the force due to pressure πr²p. This is balanced by the stress developed in the walls, acting on the circumference of the circle 2πrtσ. Thus the stress in the longitudinal direction is pr/2t. For the tangential direction, the pressure force is π2rl and the stress force is 2tlσ. The stress is pr/t.

Specific aspects of strength

Brittle materials

When for a particular property a material shows a large scatter in measured data (e.g. strength measurement results of brittle materials, or of threads with important variations in thickness), a characteristic value for, or the weakest link of such a property can be obtained by analyzing the measured data on the basis of three parameter Weibull statistics.