Strength of Materials/Introduction

Strength of Materials

Strength of Materials in Engineering Mechanics

Introduction | Introductory Concepts | Loading of Beams | Torsion | General State of Stress | Weakest link determination by use of three parameter Weibull statistics

next →  

Solid Mechanics is the study of load carrying members in terms of forces, deformations, and stability. There are three length scales: Atomic scale, Micro scale, Continuum scale. In this book, we take the continuum mechanics approach. We will consider the material to be homogeneous and isotropic (unless specified). Thus the material properties are even when we consider infinitesimal areas and volumes. The alternative approach is to build up material properties from basic equations relating atomic forces and interactions, and extending it to larger sets of such entities (e.g., ab-initio, molecular dynamics). Other approaches include micro-scale theories like dislocations to explain behavior of materials, especially for plasticity. However, the approach in this book is applicable to a large variety of practical problems, where we deal with structural members, usually under elastic deformation.

Body with Forces acting on it

Body with external forces and reactions

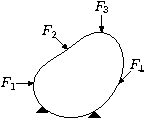
The images on the right show a body which is acted upon by external forces $\mathbf {F} _{1}\,$, $\mathbf {F} _{2}\,$, etc. The supports provide reaction forces ($\mathbf {R} _{1}\,$, $\mathbf {R} _{2}\,$) so that the body is stationary.

In addition to external forces, which act at points on the surface, we can also have forces which are body forces ($\mathbf {b} \,$), i.e., they act on each point in the body. Forces acting at a distance (Eg: Gravity, Magnetic) can be examples of body forces.

Consider a body which has several external forces acting on it. If a body is in static equilibrium, then every section of the body should also be in static equilibrium. Now, consider an elemental area dA in that section. Let the force acting on the elemental area so that the whole body is in equilibrium be dF. We can resolve this force in three mutually perpendicular directions. Let the component of the force normal to the surface be dF_z. Let the components in the plane of dA be dF_x and dF_y respectively. Then for the body to be in static equilibrium, we should have:

$\sum {\mathbf {dF} _{i}}=0,i=1,2,3$

There are three other conditions concerned with moments for completely defining static equilibrium. We will look in to it in the later chapters.