Linear Algebra/Projection Onto a Subspace

This subsection, like the others in this section, is optional. It also requires material from the optional earlier subsection on Combining Subspaces.

The prior subsections project a vector onto a line by decomposing it into two parts: the part in the line ${\mbox{proj}}_{[{\vec {s}}\,]}({{\vec {v}}\,})$ and the rest ${\vec {v}}-{\mbox{proj}}_{[{\vec {s}}\,]}({{\vec {v}}\,})$. To generalize projection to arbitrary subspaces, we follow this idea.

Definition 3.1

For any direct sum $V=M\oplus N$ and any ${\vec {v}}\in V$, the projection of ${\vec {v}}$ onto $M$ along $N$ is

${\mbox{proj}}_{M,N}({{\vec {v}}\,})={\vec {m}}$

where ${\vec {v}}={\vec {m}}+{\vec {n}}$ with ${\vec {m}}\in M,\,{\vec {n}}\in N$.

This definition doesn't involve a sense of "orthogonal" so we can apply it to spaces other than subspaces of an $\mathbb {R} ^{n}$. (Definitions of orthogonality for other spaces are perfectly possible, but we haven't seen any in this book.)

Example 3.2

The space ${\mathcal {M}}_{2\!\times \!2}$ of $2\!\times \!2$ matrices is the direct sum of these two.

$M=\{{\begin{pmatrix}a&b\\0&0\end{pmatrix}}\,{\big |}\,a,b\in \mathbb {R} \}\qquad N=\{{\begin{pmatrix}0&0\\c&d\end{pmatrix}}\,{\big |}\,c,d\in \mathbb {R} \}$

To project

$A={\begin{pmatrix}3&1\\0&4\end{pmatrix}}$

onto $M$ along $N$, we first fix bases for the two subspaces.

$B_{M}=\langle {\begin{pmatrix}1&0\\0&0\end{pmatrix}},{\begin{pmatrix}0&1\\0&0\end{pmatrix}}\rangle \qquad B_{N}=\langle {\begin{pmatrix}0&0\\1&0\end{pmatrix}},{\begin{pmatrix}0&0\\0&1\end{pmatrix}}\rangle$

The concatenation of these

$B=B_{M}\!{\mathbin {{}^{\frown }}}\!B_{N}=\langle {\begin{pmatrix}1&0\\0&0\end{pmatrix}},{\begin{pmatrix}0&1\\0&0\end{pmatrix}},{\begin{pmatrix}0&0\\1&0\end{pmatrix}},{\begin{pmatrix}0&0\\0&1\end{pmatrix}}\rangle$

is a basis for the entire space, because the space is the direct sum, so we can use it to represent $A$.

${\begin{pmatrix}3&1\\0&4\end{pmatrix}}=3\cdot {\begin{pmatrix}1&0\\0&0\end{pmatrix}}+1\cdot {\begin{pmatrix}0&1\\0&0\end{pmatrix}}+0\cdot {\begin{pmatrix}0&0\\1&0\end{pmatrix}}+4\cdot {\begin{pmatrix}0&0\\0&1\end{pmatrix}}$

Now the projection of $A$ onto $M$ along $N$ is found by keeping the $M$ part of this sum and dropping the $N$ part.

${\mbox{proj}}_{M,N}({\begin{pmatrix}3&1\\0&4\end{pmatrix}})=3\cdot {\begin{pmatrix}1&0\\0&0\end{pmatrix}}+1\cdot {\begin{pmatrix}0&1\\0&0\end{pmatrix}}={\begin{pmatrix}3&1\\0&0\end{pmatrix}}$

Example 3.3

Both subscripts on ${\mbox{proj}}_{M,N}({{\vec {v}}\,})$ are significant. The first subscript $M$ matters because the result of the projection is an ${\vec {m}}\in M$, and changing this subspace would change the possible results. For an example showing that the second subscript matters, fix this plane subspace of $\mathbb {R} ^{3}$ and its basis

$M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,y-2z=0\}\qquad B_{M}=\langle {\begin{pmatrix}1\\0\\0\end{pmatrix}},{\begin{pmatrix}0\\2\\1\end{pmatrix}}\rangle$

and compare the projections along two different subspaces.

$N=\{k{\begin{pmatrix}0\\0\\1\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}\qquad {\hat {N}}=\{k{\begin{pmatrix}0\\1\\-2\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}$

(Verification that $\mathbb {R} ^{3}=M\oplus N$ and $\mathbb {R} ^{3}=M\oplus {\hat {N}}$ is routine.) We will check that these projections are different by checking that they have different effects on this vector.

${\vec {v}}={\begin{pmatrix}2\\2\\5\end{pmatrix}}$

For the first one we find a basis for $N$

$B_{N}=\langle {\begin{pmatrix}0\\0\\1\end{pmatrix}}\rangle$

and represent ${\vec {v}}$ with respect to the concatenation $B_{M}\!{\mathbin {{}^{\frown }}}\!B_{N}$.

${\begin{pmatrix}2\\2\\5\end{pmatrix}}=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+1\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}+4\cdot {\begin{pmatrix}0\\0\\1\end{pmatrix}}$

The projection of ${\vec {v}}$ onto $M$ along $N$ is found by keeping the $M$ part and dropping the $N$ part.

${\mbox{proj}}_{M,N}({{\vec {v}}\,})=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+1\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}={\begin{pmatrix}2\\2\\1\end{pmatrix}}$

For the other subspace ${\hat {N}}$, this basis is natural.

$B_{\hat {N}}=\langle {\begin{pmatrix}0\\1\\-2\end{pmatrix}}\rangle$

Representing ${\vec {v}}$ with respect to the concatenation

${\begin{pmatrix}2\\2\\5\end{pmatrix}}=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+(9/5)\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}-(8/5)\cdot {\begin{pmatrix}0\\1\\-2\end{pmatrix}}$

and then keeping only the $M$ part gives this.

${\mbox{proj}}_{M,{\hat {N}}}({{\vec {v}}\,})=2\cdot {\begin{pmatrix}1\\0\\0\end{pmatrix}}+(9/5)\cdot {\begin{pmatrix}0\\2\\1\end{pmatrix}}={\begin{pmatrix}2\\18/5\\9/5\end{pmatrix}}$

Therefore projection along different subspaces may yield different results.

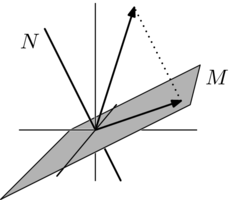
These pictures compare the two maps. Both show that the projection is indeed "onto" the plane and "along" the line.

Notice that the projection along $N$ is not orthogonal— there are members of the plane $M$ that are not orthogonal to the dotted line. But the projection along ${\hat {N}}$ is orthogonal.

A natural question is: what is the relationship between the projection operation defined above, and the operation of orthogonal projection onto a line? The second picture above suggests the answer— orthogonal projection onto a line is a special case of the projection defined above; it is just projection along a subspace perpendicular to the line.

In addition to pointing out that projection along a subspace is a generalization, this scheme shows how to define orthogonal projection onto any subspace of $\mathbb {R} ^{n}$, of any dimension.

Definition 3.4

The orthogonal complementof a subspace $M$ of $\mathbb {R} ^{n}$ is

$M^{\perp }=\{{\vec {v}}\in \mathbb {R} ^{n}\,{\big |}\,{\vec {v}}{\text{ is perpendicular to all vectors in }}M\}$

(read "$M$ perp"). The orthogonal projection ${\mbox{proj}}_{M}({{\vec {v}}\,})$ of a vector is its projection onto $M$ along $M^{\perp }$.

Example 3.5

In $\mathbb {R} ^{3}$, to find the orthogonal complement of the plane

$P=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,3x+2y-z=0\}$

we start with a basis for $P$.

$B=\langle {\begin{pmatrix}1\\0\\3\end{pmatrix}},{\begin{pmatrix}0\\1\\2\end{pmatrix}}\rangle$

Any ${\vec {v}}$ perpendicular to every vector in $B$ is perpendicular to every vector in the span of $B$ (the proof of this assertion is Problem 10). Therefore, the subspace $P^{\perp }$ consists of the vectors that satisfy these two conditions.

${\begin{pmatrix}1\\0\\3\end{pmatrix}}\cdot {\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}=0\qquad {\begin{pmatrix}0\\1\\2\end{pmatrix}}\cdot {\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}=0$

We can express those conditions more compactly as a linear system.

$P^{\perp }=\{{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\,{\big |}\,{\begin{pmatrix}1&0&3\\0&1&2\end{pmatrix}}{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}\}$

We are thus left with finding the nullspace of the map represented by the matrix, that is, with calculating the solution set of a homogeneous linear system.

$P^{\perp }=\{{\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\,{\big |}\,\;{\begin{array}{*{3}{rc}r}v_{1}&&&+&3v_{3}&=&0\\&&v_{2}&+&2v_{3}&=&0\end{array}}\;\}=\{k{\begin{pmatrix}-3\\-2\\1\end{pmatrix}}\,{\big |}\,k\in \mathbb {R} \}$

Example 3.6

Where $M$ is the $xy$-plane subspace of $\mathbb {R} ^{3}$, what is $M^{\perp }$? A common first reaction is that $M^{\perp }$ is the $yz$-plane, but that's not right. Some vectors from the $yz$-plane are not perpendicular to every vector in the $xy$-plane.

${\begin{pmatrix}1\\1\\0\end{pmatrix}}\not \perp {\begin{pmatrix}0\\3\\2\end{pmatrix}}$

$\displaystyle \theta =\arccos({\frac {1\cdot 0+1\cdot 3+0\cdot 2}{{\sqrt {2}}\cdot {\sqrt {13}}}})\approx {\text{0.94 rad}}$

Instead $M^{\perp }$ is the $z$-axis, since proceeding as in the prior example and taking the natural basis for the $xy$-plane gives this.

$M^{\perp }=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,{\begin{pmatrix}1&0&0\\0&1&0\end{pmatrix}}{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}\;\}=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x=0{\text{ and }}y=0\}$

The two examples that we've seen since Definition 3.4 illustrate the first sentence in that definition. The next result justifies the second sentence.

Lemma 3.7

Let $M$ be a subspace of $\mathbb {R} ^{n}$. The orthogonal complement of $M$ is also a subspace. The space is the direct sum of the two $\mathbb {R} ^{n}=M\oplus M^{\perp }$. And, for any ${\vec {v}}\in \mathbb {R} ^{n}$, the vector ${\vec {v}}-{\mbox{proj}}_{M}({{\vec {v}}\,})$ is perpendicular to every vector in $M$.

Proof

First, the orthogonal complement $M^{\perp }$ is a subspace of $\mathbb {R} ^{n}$ because, as noted in the prior two examples, it is a nullspace.

Next, we can start with any basis $B_{M}=\langle {\vec {\mu }}_{1},\dots ,{\vec {\mu }}_{k}\rangle$ for $M$ and expand it to a basis

for the entire space. Apply the Gram-Schmidt process to get an orthogonal basis $K=\langle {\vec {\kappa }}_{1},\dots ,{\vec {\kappa }}_{n}\rangle$ for $\mathbb {R} ^{n}$. This $K$ is the concatenation of two bases $\langle {\vec {\kappa }}_{1},\dots ,{\vec {\kappa }}_{k}\rangle$ (with the same number of members as $B_{M}$) and $\langle {\vec {\kappa }}_{k+1},\dots ,{\vec {\kappa }}_{n}\rangle$. The first is a basis for $M$, so if we show that the second is a basis for $M^{\perp }$ then we will have that the entire space is the direct sum of the two subspaces.

Problem 9 from the prior subsection proves this about any orthogonal basis: each vector ${\vec {v}}$ in the space is the sum of its orthogonal projections onto the lines spanned by the basis vectors.

${\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{n}]}({{\vec {v}}\,})\qquad \qquad (*)$

To check this, represent the vector ${\vec {v}}=r_{1}{\vec {\kappa }}_{1}+\dots +r_{n}{\vec {\kappa }}_{n}$, apply ${\vec {\kappa }}_{i}$ to both sides ${\vec {v}}\cdot {\vec {\kappa }}_{i}=\left(r_{1}{\vec {\kappa }}_{1}+\dots +r_{n}{\vec {\kappa }}_{n}\right)\cdot {\vec {\kappa }}_{i}=r_{1}\cdot 0+\dots +r_{i}\cdot ({\vec {\kappa }}_{i}\cdot {\vec {\kappa }}_{i})+\dots +r_{n}\cdot 0$, and solve to get $r_{i}=({\vec {v}}\cdot {\vec {\kappa }}_{i})/({\vec {\kappa }}_{i}\cdot {\vec {\kappa }}_{i})$, as desired.

Since obviously any member of the span of $\langle {\vec {\kappa }}_{k+1},\dots ,{\vec {\kappa }}_{n}\rangle$ is orthogonal to any vector in $M$, to show that this is a basis for $M^{\perp }$ we need only show the other containment— that any ${\vec {w}}\in M^{\perp }$ is in the span of this basis. The prior paragraph does this. On projections onto basis vectors from $M$, any ${\vec {w}}\in M^{\perp }$ gives ${\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {w}}\,})={\vec {0}},\dots ,\,{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {w}}\,})={\vec {0}}$ and therefore ($*$) gives that ${\vec {w}}$ is a linear combination of ${\vec {\kappa }}_{k+1},\dots ,{\vec {\kappa }}_{n}$. Thus this is a basis for $M^{\perp }$ and $\mathbb {R} ^{n}$ is the direct sum of the two.

The final sentence is proved in much the same way. Write ${\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{n}]}({{\vec {v}}\,})$. Then ${\mbox{proj}}_{M}({{\vec {v}}\,})$ is gotten by keeping only the $M$ part and dropping the $M^{\perp }$ part ${\mbox{proj}}_{M}({{\vec {v}}\,})={\mbox{proj}}_{[{\vec {\kappa }}_{k+1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {v}}\,})$. Therefore ${\vec {v}}-{\mbox{proj}}_{M}({{\vec {v}}\,})$ consists of a linear combination of elements of $M^{\perp }$ and so is perpendicular to every vector in $M$.

We can find the orthogonal projection onto a subspace by following the steps of the proof, but the next result gives a convienent formula.

Theorem 3.8

Let ${\vec {v}}$ be a vector in $\mathbb {R} ^{n}$ and let $M$ be a subspace of $\mathbb {R} ^{n}$ with basis $\langle {\vec {\beta }}_{1},\dots ,{\vec {\beta }}_{k}\rangle$. If $A$ is the matrix whose columns are the ${\vec {\beta }}$'s then ${\mbox{proj}}_{M}({{\vec {v}}\,})=c_{1}{\vec {\beta }}_{1}+\dots +c_{k}{\vec {\beta }}_{k}$ where the coefficients $c_{i}$ are the entries of the vector $({{A}^{\rm {trans}}}A)^{-1}{{A}^{\rm {trans}}}\cdot {\vec {v}}$. That is, ${\mbox{proj}}_{M}({{\vec {v}}\,})=A({{A}^{\rm {trans}}}A)^{-1}{{A}^{\rm {trans}}}\cdot {\vec {v}}$.

Proof

The vector ${\mbox{proj}}_{M}({\vec {v}})$ is a member of $M$ and so it is a linear combination of basis vectors $c_{1}\cdot {\vec {\beta }}_{1}+\dots +c_{k}\cdot {\vec {\beta }}_{k}$. Since $A$'s columns are the ${\vec {\beta }}$'s, that can be expressed as: there is a ${\vec {c}}\in \mathbb {R} ^{k}$ such that ${\mbox{proj}}_{M}({{\vec {v}}\,})=A{\vec {c}}$ (this is expressed compactly with matrix multiplication as in Example 3.5 and 3.6). Because ${\vec {v}}-{\mbox{proj}}_{M}({{\vec {v}}\,})$ is perpendicular to each member of the basis, we have this (again, expressed compactly).

${\vec {0}}={{A}^{\rm {trans}}}{\bigl (}{\vec {v}}-A{\vec {c}}{\bigr )}={{A}^{\rm {trans}}}{\vec {v}}-{{A}^{\rm {trans}}}A{\vec {c}}$

Solving for ${\vec {c}}$ (showing that ${{A}^{\rm {trans}}}A$ is invertible is an exercise)

${\vec {c}}={\bigl (}{{A}^{\rm {trans}}}A{\bigr )}^{-1}{{A}^{\rm {trans}}}\cdot {\vec {v}}$

gives the formula for the projection matrix as ${\mbox{proj}}_{M}({{\vec {v}}\,})=A\cdot {\vec {c}}$.

Example 3.9

To orthogonally project this vector onto this subspace

${\vec {v}}={\begin{pmatrix}1\\-1\\1\end{pmatrix}}\qquad P=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x+z=0\}$

first make a matrix whose columns are a basis for the subspace

$A={\begin{pmatrix}0&1\\1&0\\0&-1\end{pmatrix}}$

and then compute.

${\begin{array}{rl}A{\bigl (}{{A}^{\rm {trans}}}A{\bigr )}^{-1}{{A}^{\rm {trans}}}&={\begin{pmatrix}0&1\\1&0\\0&-1\end{pmatrix}}{\begin{pmatrix}0&1\\1/2&0\end{pmatrix}}{\begin{pmatrix}1&0&-1\\0&1&0\end{pmatrix}}\\&={\begin{pmatrix}1/2&0&-1/2\\0&1&0\\-1/2&0&1/2\end{pmatrix}}\end{array}}$

With the matrix, calculating the orthogonal projection of any vector onto $P$ is easy.

${\mbox{proj}}_{P}({\vec {v}})={\begin{pmatrix}1/2&0&-1/2\\0&1&0\\-1/2&0&1/2\end{pmatrix}}{\begin{pmatrix}1\\-1\\1\end{pmatrix}}={\begin{pmatrix}0\\-1\\0\end{pmatrix}}$

Exercises

This exercise is recommended for all readers.

Problem 1

Project the vectors onto $M$ along $N$.

1. ${\begin{pmatrix}3\\-2\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x+y=0\},\quad N=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,-x-2y=0\}$
2. ${\begin{pmatrix}1\\2\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x-y=0\},\quad N=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,2x+y=0\}$
3. ${\begin{pmatrix}3\\0\\1\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x+y=0\},\quad N=\{c\cdot {\begin{pmatrix}1\\0\\1\end{pmatrix}}\,{\big |}\,c\in \mathbb {R} \}$

This exercise is recommended for all readers.

Problem 2

Find $M^{\perp }$.

1. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x+y=0\}$
2. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,-2x+3y=0\}$
3. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x-y=0\}$
4. $M=\{{\vec {0}}\,\}$
5. $M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x=0\}$
6. $M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,-x+3y+z=0\}$
7. $M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x=0{\text{ and }}y+z=0\}$

Problem 3

This subsection shows how to project orthogonally in two ways, the method of Example 3.2 and 3.3, and the method of Theorem 3.8. To compare them, consider the plane $P$ specified by $3x+2y-z=0$ in $\mathbb {R} ^{3}$.

1. Find a basis for $P$.
2. Find $P^{\perp }$ and a basis for $P^{\perp }$.
3. Represent this vector with respect to the concatenation of the two bases from the prior item.

   ${\vec {v}}={\begin{pmatrix}1\\1\\2\end{pmatrix}}$

4. Find the orthogonal projection of ${\vec {v}}$ onto $P$ by keeping only the $P$ part from the prior item.
5. Check that against the result from applying Theorem 3.8.

This exercise is recommended for all readers.

Problem 4

We have three ways to find the orthogonal projection of a vector onto a line, the Definition 1.1 way from the first subsection of this section, the Example 3.2 and 3.3 way of representing the vector with respect to a basis for the space and then keeping the $M$ part, and the way of Theorem 3.8. For these cases, do all three ways.

1. ${\vec {v}}={\begin{pmatrix}1\\-3\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\end{pmatrix}}\,{\big |}\,x+y=0\}$
2. ${\vec {v}}={\begin{pmatrix}0\\1\\2\end{pmatrix}},\quad M=\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}\,{\big |}\,x+z=0{\text{ and }}y=0\}$

Problem 5

Check that the operation of Definition 3.1 is well-defined. That is, in Example 3.2 and 3.3, doesn't the answer depend on the choice of bases?

Problem 6

What is the orthogonal projection onto the trivial subspace?

Problem 7

What is the projection of ${\vec {v}}$ onto $M$ along $N$ if ${\vec {v}}\in M$?

Problem 8

Show that if $M\subseteq \mathbb {R} ^{n}$ is a subspace with orthonormal basis $\langle {\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{n}\rangle$ then the orthogonal projection of ${\vec {v}}$ onto $M$ is this.

$({\vec {v}}\cdot {\vec {\kappa }}_{1})\cdot {\vec {\kappa }}_{1}+\dots +({\vec {v}}\cdot {\vec {\kappa }}_{n})\cdot {\vec {\kappa }}_{n}$

This exercise is recommended for all readers.

Problem 9

Prove that the map $p:V\to V$ is the projection onto $M$ along $N$ if and only if the map ${\mbox{id}}-p$ is the projection onto $N$ along $M$. (Recall the definition of the difference of two maps: $({\mbox{id}}-p)\,({\vec {v}})={\mbox{id}}({\vec {v}})-p({\vec {v}})={\vec {v}}-p({\vec {v}})$.)

This exercise is recommended for all readers.

Problem 10

Show that if a vector is perpendicular to every vector in a set then it is perpendicular to every vector in the span of that set.

Problem 11

True or false: the intersection of a subspace and its orthogonal complement is trivial.

Problem 12

Show that the dimensions of orthogonal complements add to the dimension of the entire space.

This exercise is recommended for all readers.

Problem 13

Suppose that ${\vec {v}}_{1},{\vec {v}}_{2}\in \mathbb {R} ^{n}$ are such that for all complements $M,N\subseteq \mathbb {R} ^{n}$, the projections of ${\vec {v}}_{1}$ and ${\vec {v}}_{2}$ onto $M$ along $N$ are equal. Must ${\vec {v}}_{1}$ equal ${\vec {v}}_{2}$? (If so, what if we relax the condition to: all orthogonal projections of the two are equal?)

This exercise is recommended for all readers.

Problem 14

Let $M,N$ be subspaces of $\mathbb {R} ^{n}$. The perp operator acts on subspaces; we can ask how it interacts with other such operations.

1. Show that two perps cancel: $(M^{\perp })^{\perp }=M$.
2. Prove that $M\subseteq N$ implies that $N^{\perp }\subseteq M^{\perp }$.
3. Show that $(M+N)^{\perp }=M^{\perp }\cap N^{\perp }$.

This exercise is recommended for all readers.

Problem 15

The material in this subsection allows us to express a geometric relationship that we have not yet seen between the rangespace and the nullspace of a linear map.

1. Represent $f:\mathbb {R} ^{3}\to \mathbb {R}$ given by

   ${\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\mapsto 1v_{1}+2v_{2}+3v_{3}$

   with respect to the standard bases and show that

   ${\begin{pmatrix}1\\2\\3\end{pmatrix}}$

   is a member of the perp of the nullspace. Prove that ${\mathcal {N}}(f)^{\perp }$ is equal to the span of this vector.
2. Generalize that to apply to any $f:\mathbb {R} ^{n}\to \mathbb {R}$.
3. Represent $f:\mathbb {R} ^{3}\to \mathbb {R} ^{2}$

   ${\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}\mapsto {\begin{pmatrix}1v_{1}+2v_{2}+3v_{3}\\4v_{1}+5v_{2}+6v_{3}\end{pmatrix}}$

   with respect to the standard bases and show that

   ${\begin{pmatrix}1\\2\\3\end{pmatrix}},\;{\begin{pmatrix}4\\5\\6\end{pmatrix}}$

   are both members of the perp of the nullspace. Prove that ${\mathcal {N}}(f)^{\perp }$ is the span of these two. (Hint. See the third item of Problem 14.)
4. Generalize that to apply to any $f:\mathbb {R} ^{n}\to \mathbb {R} ^{m}$.

This, and related results, is called the Fundamental Theorem of Linear Algebra in (Strang 1993).

Problem 16

Define a projection to be a linear transformation $t:V\to V$ with the property that repeating the projection does nothing more than does the projection alone: $(t\circ t)\,({\vec {v}})=t({\vec {v}})$ for all ${\vec {v}}\in V$.

1. Show that orthogonal projection onto a line has that property.
2. Show that projection along a subspace has that property.
3. Show that for any such $t$ there is a basis $B=\langle {\vec {\beta }}_{1},\ldots ,{\vec {\beta }}_{n}\rangle$ for $V$ such that

   $t({\vec {\beta }}_{i})={\begin{cases}{\vec {\beta }}_{i}&i=1,2,\dots ,\,r\\{\vec {0}}&i=r+1,r+2,\dots ,\,n\end{cases}}$

   where $r$ is the rank of $t$.
4. Conclude that every projection is a projection along a subspace.
5. Also conclude that every projection has a representation

   ${\rm {Rep}}_{B,B}(t)=\left({\begin{array}{c|c}I&Z\\\hline Z&Z\end{array}}\right)$

   in block partial-identity form.

Problem 17

A square matrix is symmetric if each $i,j$ entry equals the $j,i$ entry (i.e., if the matrix equals its transpose). Show that the projection matrix $A({{A}^{\rm {trans}}}A)^{-1}{{A}^{\rm {trans}}}$ is symmetric. (Strang 1980) Hint. Find properties of transposes by looking in the index under "transpose".

Solutions

References

• Strang, Gilbert (1993), "The Fundamental Theorem of Linear Algebra", American Mathematical Monthly, American Mathematical Society: 848–855 {{citation}}: Unknown parameter |month= ignored (help).
• Strang, Gilbert (1980), Linear Algebra and its Applications (2nd ed.), Hartcourt Brace Javanovich