GLSL Programming/Blender/Reflecting Surfaces
This tutorial introduces reflection mapping (and cube maps to implement it).
It's the second in a small series of tutorials about advanced texture mapping techniques; specifically about environment mapping using cube maps in Blender. The tutorial is based on the per-pixel lighting described in the tutorial on smooth specular highlights and on the concept of texture mapping, which was introduced in the tutorial on textured spheres.
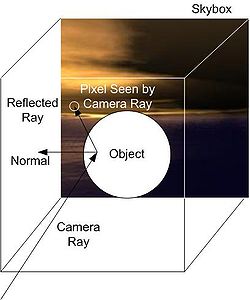
Reflection Mapping with a Skybox
editThe illustration to the left depicts the concept of reflection mapping with a static skybox: a view ray is reflected at a point on the surface of an object and the reflected ray is intersected with the skybox to determine the color of the corresponding pixel. The skybox is just a large cube with textured faces surrounding the whole scene. It should be noted that skyboxes are usually static and don't include any dynamic objects of the scene. However, “skyboxes” for reflection mapping are often rendered to include the scene from a certain point of view. This is, however, beyond the scope of this tutorial. Moreover, this tutorial covers only the computation of the reflection, it doesn't cover the rendering of the skybox.
For the reflection of a skybox in an object, we have to render the object and reflect the rays from the camera to the surface points at the surface normal vectors. The mathematics of this reflection is the same as for the reflection of a light ray at a surface normal vector, which was discussed in the tutorial on specular highlights.
Once we have the reflected ray, its intersection with a large skybox has to be computed. This computation actually becomes easier if the skybox is infinitely large: in that case the position of the surface point doesn't matter at all since its distance from the origin of the coordinate system is infinitely small compared to the size of the skybox; thus, only the direction of the reflected ray matters but not its position. Therefore, we can actually also think of a ray that starts in the center of a small skybox instead of a ray that starts somewhere in an infinitely large skybox. (If you are not familiar with this idea, you probably need a bit of time to accept it.) Depending on the direction of the reflected ray, it will intersect one of the six faces of the textured skybox. We could compute, which face is intersected and where the face is intersected and then do a texture lookup (see the tutorial on textures spheres) in the texture image for the specific face. However, GLSL offers cube maps, which support exactly this kind of texture lookups in the six faces of a cube using a direction vector. Thus, all we need to do, is to provide a cube map for the environment as a shader property and use the textureCube instruction with the reflected direction to get the color at the corresponding position in the cube map.
Cube Maps
editThe image to the left shows a Blender cube map, which is discussed in the wikibook “Blender 3D Noob to Pro”. Actually, it is a scaled version of the cube map that is described in the Blender wikibook because the dimensions of faces of cube maps for GLSL shaders have to be powers of two, e.g. 128 × 128.
In order to use the cube map to the left for the reflection in a sphere, add a UV sphere mesh, give it a material and create a new texture as in the tutorial on textures spheres. However, in the Properties window > Textures tab choose Type: Environment Map and click on Environment Map > Image File. Then download the image and open it in Blender with the Environment Map > Open button. (If you select Mapping > Coordinates: Reflection, the Preview > Material should show the applied reflection map.)
The vertex shader has to compute the view direction viewDirection and the normal direction normalDirection in world space. We saw how to compute them in view space in the tutorial on specular highlights. Therefore, we use this code to go to world space and then back to view space by transforming with the inverse view matrix as discussed in the tutorial on shading in view space. An additional complication is that the normal vector has to be transformed with the transposed, inverse matrix (see “Applying Matrix Transformations”). In this case, the inverse matrix is the inverse of the inverse view matrix, which is just the view matrix itself. Thus the vertex shader could be:
uniform mat4 viewMatrix; // world to view transformation
uniform mat4 viewMatrixInverse;
// view to world transformation
varying vec3 viewDirection; // direction in world space
// in which the viewer is looking
varying vec3 normalDirection; // normal vector in world space
void main()
{
vec4 positionInViewSpace = gl_ModelViewMatrix * gl_Vertex;
// transformation of gl_Vertex from object coordinates
// to view coordinates
vec4 viewDirectionInViewSpace = positionInViewSpace
- vec4(0.0, 0.0, 0.0, 1.0);
// camera is always at (0,0,0,1) in view coordinates;
// this is the direction in which the viewer is looking
// (not the direction to the viewer)
viewDirection =
vec3(viewMatrixInverse * viewDirectionInViewSpace);
// transformation from view coordinates to
// world coordinates
vec3 normalDirectionInViewSpace =
gl_NormalMatrix * gl_Normal;
// transformation of gl_Normal from object coordinates
// to view coordinates
normalDirection = normalize(vec3(
vec4(normalDirectionInViewSpace, 0.0) * viewMatrix));
// transformation of normal vector from view coordinates
// to world coordinates with the transposed
// (multiplication of the vector from the left) of
// the inverse of viewMatrixInverse, which is viewMatrix
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
Furthermore, we have to set the uniforms for viewMatrix and viewMatrixInverse in the Python script:
viewMatrix = \
bge.logic.getCurrentScene().active_camera.world_to_camera
shader.setUniformMatrix4('viewMatrix', viewMatrix)
viewMatrixInverse = \
bge.logic.getCurrentScene().active_camera.camera_to_world
shader.setUniformMatrix4('viewMatrixInverse', viewMatrixInverse)
Now to the fragment shader. A cube map is defined similarly to a regular 2D texture in a GLSL shader but with samplerCube instead of sampler2D:
uniform samplerCube cubeMap;
The uniform is set in the Python script just like any other texture sampler:
shader.setSampler('cubeMap', 0)
Where the 0 specifies the position in the list of textures.
To reflect the view direction in the fragment shader, we can use the GLSL function reflect as discussed in the tutorial on specular highlights:
vec3 reflectedDirection =
reflect(viewDirection, normalize(normalDirection));
And to perform the texture lookup in the cube map and store the resulting color in the fragment color, we would usually simply use:
gl_FragColor = textureCube(cubeMap, reflectedDirection);
However, Blender appears to reshuffle the cube faces; thus, we have to adapt the coordinates of reflectedDirection:
gl_FragColor = textureCube(cubeMap,
vec3(reflectedDirection.x, -reflectedDirection.z,
reflectedDirection.y));
This produces a reflection that is consistent with the material preview.
Complete Shader Code
editThe shader code then becomes:
import bge
cont = bge.logic.getCurrentController()
VertexShader = """
uniform mat4 viewMatrix; // world to view transformation
uniform mat4 viewMatrixInverse;
// view to world transformation
varying vec3 viewDirection; // direction in world space
// in which the viewer is looking
varying vec3 normalDirection; // normal vector in world space
void main()
{
vec4 positionInViewSpace = gl_ModelViewMatrix * gl_Vertex;
// transformation of gl_Vertex from object coordinates
// to view coordinates
vec4 viewDirectionInViewSpace = positionInViewSpace
- vec4(0.0, 0.0, 0.0, 1.0);
// camera is always at (0,0,0,1) in view coordinates;
// this is the direction in which the viewer is looking
// (not the direction to the viewer)
viewDirection =
vec3(viewMatrixInverse * viewDirectionInViewSpace);
// transformation from view coordinates
// to world coordinates
vec3 normalDirectionInViewSpace =
gl_NormalMatrix * gl_Normal;
// transformation of gl_Normal from object coordinates
// to view coordinates
normalDirection = normalize(vec3(
vec4(normalDirectionInViewSpace, 0.0) * viewMatrix));
// transformation of normal vector from view coordinates
// to world coordinates with the transposed
// (multiplication of the vector from the left) of
// the inverse of viewMatrixInverse, which is viewMatrix
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
"""
FragmentShader = """
varying vec3 viewDirection;
varying vec3 normalDirection;
uniform samplerCube cubeMap;
void main()
{
vec3 reflectedDirection = reflect(viewDirection,
normalize(normalDirection));
gl_FragColor = textureCube(cubeMap,
vec3(reflectedDirection.x, -reflectedDirection.z,
reflectedDirection.y));
// usually this would be: gl_FragColor =
// textureCube(cubeMap, reflectedDirection);
// however, Blender appears to reshuffle the faces a bit
}
"""
mesh = cont.owner.meshes[0]
for mat in mesh.materials:
shader = mat.getShader()
if shader != None:
if not shader.isValid():
shader.setSource(VertexShader, FragmentShader, 1)
shader.setSampler('cubeMap', 0)
viewMatrix = \
bge.logic.getCurrentScene().active_camera.world_to_camera
shader.setUniformMatrix4('viewMatrix', viewMatrix)
viewMatrixInverse = \
bge.logic.getCurrentScene().active_camera.camera_to_world
shader.setUniformMatrix4('viewMatrixInverse', \
viewMatrixInverse)
Summary
editCongratulations! You have reached the end of the first tutorial on environment maps. We have seen:
- How to compute the reflection of a skybox in an object.
- How to import suitable cube maps in Blender and how to use them for reflection mapping.
Further Reading
editIf you still want to know more
- about the reflection of vectors, you should read the tutorial on specular highlights.
- about obtaining the (inverse) view matrix in Python, you should read the tutorial on shading in view space.
- about transforming normal vectors (with the transposed, inverse matrix), you should read “Applying Matrix Transformations”.
- about texturing with two-dimensional texture images, you should read the tutorial on textured spheres.
- about cube maps in Blender, you could read the section “Build a skybox” in the Blender 3D wikibook.