Engineering Acoustics/Conductive Mechanisms of Hearing

In this section we will discuss the pathways for conduction of acoustic sound waves to the inner ear. Two methods of conduction will be covered; first we will cover conduction to the inner ear through the outer and middle ear then conduction to the inner ear through bone conduction. Without these conductive pathways the acoustic waves that transmit sound would not be able to reach the inner ear, and we would therefore be unable to hear.

Anatomy of the Human Ear

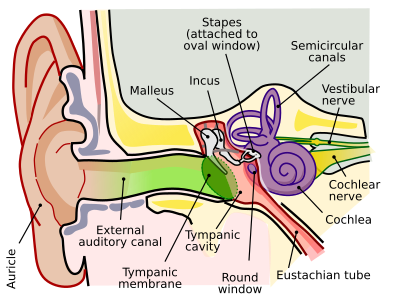
Outer Ear

The first area where sound enters the ear is in the outer ear which can be broken down into two parts, the Pinna (visible portion of the ear) and the ear canal.

Pinna

It was once thought that the Pinna funneled sound into the ear canal, but the primary function of the Pinna is to aid in sound source localization. The various ridges in the Pinna filter the signal at frequencies over 4000 Hz according to the direction of the sound.The resulting spectral variations allow our brain to determine the elevation of a sound and localize sounds in reference to our position.

Ear Canal

The ear canal can be modeled as a tube approximately 2.8 cm long that is closed at one end by the tympanic membrane. Unlike a rigid tube that has a sharp spike in amplitude at the resonant frequency, the ear canal has a wide resonance peak from approximately 2–5 kHz. It is important to remember the ear canal is not rigid nor is not a straight tube, and therefore damping is introduced.While damping is introduced to the system, thereby altering the resonant frequency, the important thing is that the ear canal can raise the Sound Pressure Level (SPL) of the ear by up to 15 dB which will amplify the incoming acoustic signal.

Thumb

Middle Ear

The primary purpose of the middle ear is to act as an impedance-matching transformer that will allow for acoustic energy to be efficiently transferred from the air filled outer ear to the liquid filled cochlea. Knowing the impedance ratio, r, of the liquid in the cochlea to the air is 4000:1 we can use the following equation to determine what the energy transmission coefficient, T, would be without the middle ear

$T={\frac {4r}{\left(r+1\right)^{2}}}$

which gives us a transmission of 0.001 or 0.1%. This transmission value is equivalent to a SPL drop of around 40 dB.

To overcome this impedance mismatch,the middle ear employs three mechanical amplification systems; the areal ratio between the Tympanic Membrane and the Stapes, the areal ratio of the stapes to the Oval Window the lever effect of the Ossicular Chain.

Areal Ratio

While the ossicular chain helps to increase the pressure of the incoming acoustic signal, the majority of gain in the middle ear is due to the areal ratio of the tympanic membrane and the stapes. The average area of the tympanic membrane is 66 $mm^{2}$ while that of the stapes is 3.2 $mm^{2}$. The areal ratio between the two areas should therefore be approximately 20:1, but as mentioned earlier the effective area of the tympanic membrane is only 65% so, 66 $mm^{2}$ x 65% = 42.9 $mm^{2}$. This results in an areal ratio of 13.4.

Thumb

Tympanic membrane

The tympanic membrane plays an important role in the conduction of sound. Serving as a Transducer, the membrane converts acoustic pressure waves into mechanical motion. Experiments have shown that the tympanic membrane is not uniform, but has a spatially variable stiffness. Due to these variations, the effective area of the membrane is only 65%. It is important to mention that the stiffness of the tympanic membrane is also very important to the efficient transfer of energy as being too stiff would reflect a large amount of energy back through the ear canal, while being too flacid would cause the membrane to absorb too much energy.

Another Important contribution of the Tympanic membrane is the gain contributed by the curved membrane principle. This model represents the membrane in two sections with the manubrium at the center. Due to the curved membrane principle, the force on the manubrium is greater than on the membrane and thus the strength of the incoming signal is increased by a factor of 2. Including these effects, we find the total gain of the areal ratio and tympanic membrane will be 26.8. Using this pressure ratio we can calculate the associated gain in decibels

${\text{dB Gain}}=20\,log(26.8/1)=28.6\,dB\$

Similar to the areal ratio between the tympanic membrane and the stapes, the areal ratio between the stapes and the oval window of the Cochlea is 20:1

${\text{dB Gain}}=20\,log(20/1)=26\,dB\$

Which yields a pressure gain of 26 dB.

Ossicular Chain

The ossicular chain functions like a basic lever. The manubrium of the Malleus is 1.3 times longer than the long process of the Incus, and the two ossicles are connect with ligaments so that they can move together. Their attachment in the middle ear evenly distributes their mass about an axis of rotation which allows them to be easily set into motion by incoming acoustic signals. In addition, the ossicles are damped enough that when the incoming signal is stopped, the malleus and incus stop as well which is desirable as continued motion of the ossicles would lead to echoing. The difference in lengths between the two ossicles also corresponds to a pressure gain at the incus equivalent to the length ratio of the two ossicles. This can be best shown by modeling the two bones as a simple lever:

Anatomy of the Human Ear

Knowing this pressure ratio we are able to compute the equivalent gain in decibels:

${\text{dB Gain}}=20\,log(1.3)=2.3\,dB\$

While the pressure gain is small, it still contributes to the conduction of sound to the inner ear.

Overall Middle Ear Gain/ Ideal Transformer Prediction

Using the pressure gain from the ossicular chain, the areal ratio of the tympanic membrane to the stapes, and the areal ratio of the stapes to the oval window we find the total gain from the middle ear is

${\text{Middle Ear dB Gain}}=2.3\,dB+28.6\,dB\ +26\,dB=56.9\,dB$

This gain in the middle ear is called "The Ideal Transformer Prediction...compensate[s] for the air-to-cochlea impedance mismatch" and has been confirmed in tests performed on cadavers with the middle ears removed.

Bone Conduction

Bone conduction is the transfer of sound to the cochlea through the bones of the skull. In for conduction to occur in the skull, the air-conduction threshold of sound must be exceeded by 50-60 dB which often occur through direct vibration to the skull, primarily the temporal bone. When this threshold is exceeded, the traveling waves produced in the cochlea resemble those induced by the stapes. Due to the impedance mismatch, bone conduction does not play a significant role in hearing, but is often used for measuring hearing to determine if there is damage to the middle ear, or to test the viability of the inner ear.

One use for bone conduction is with people with a damaged middle ear but having a normal functioning inner ear. For these people a traditional hearing aid can not be used, but due to a healthy inner ear bone conduction hearing aids can be. For these hearing aids a titanium screw can be implanted into the skull, and an external device housing the microphone and receiver can conduct acoustic waves to the inner ear through the temporal bone. While hearing through bone conduction is not perfect, it does allow for clear and understandable sound recognition.