Descriptive Geometry/Ruled Surfaces
A ruled surface, also known as a scroll surface S, is the result of moving a straight line along a curve. In contrast, a planar surface is the result of moving a straight line along another straight line. A ruled surface exists when every point of a surface can connect to at least one other point on the surface to make a straight line.
Examples of ruled surfaces include:
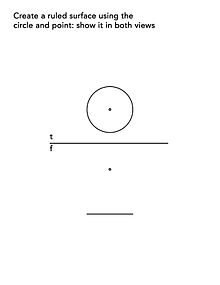
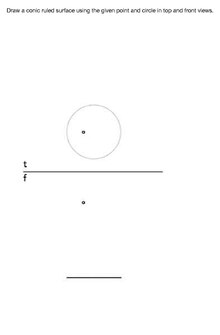
Cones- result of a line moving about a point along a circle
"Right Cones" - result of a line moving along a circle through a point which lies directly above or below the center of the circle.
"Oblique Cones" - result of a line moving along a circle through a point which does not lie directly above or below the center of the circle.
"Truncated Cones" - result of a line moving along a circle through a point, which is then truncated by a plane or another solid. To complete the view you would use the method of piercing points. (If the cutting plane is parallel to the base of a right cone, the result is a circle.)
http://www.youtube.com/watch?v=SQZIKtObIIU
Cylinders- line moving along a circle perpendicular to the circle.
"Right Cylinders" - result of a line moving along a circle parallel to an axis that is perpendicular to the plane of the circle.
"Oblique Cylinder" - result of a line moving along a circle, parallel to an axis that is NOT perpendicular to the plan of the circle.
"Truncated Cylinder" - result of a line moving along a circle parallel to an axis, which is then truncated by another plane or solid. To complete the view you would use the method of piecing points.
(If the cutting plane is parallel to the axis, the result is a parallelogram.)
http://www.youtube.com/watch?v=L-lPkWvlUYc
Real Life Example:
-
DNA Double-helix
Roller Coasters- the parallel tracks moving along the curved result of the roller coaster.
Use of Ruled Surfaces: In descriptive geometry, ruled surfaces are used to solve intersection problems. When you treat a curved surface (such as the outside of a cone or cylinder) as a series of lines you will be able to find the intersection points more easily.
Example Problems With Answers: