Descriptive Geometry/Finding distances through rotation

To find the distance between a point and a line or a point and a plane, rotate a line to find true length. With a point and a line: rotate the line perpendicular to the folding line to find the line in point view. With a point and a plane: you must rotate the line perpendicular to the folding line to find the line in edge view. From there you can measure the distance between the points or the point and the line.

Finding the Shortest Distance Between a Point and a Line:

1. Rotate the line in one of the views (of your choice), so that the line is parallel to the folding line.
2. Transfer the new point to the other view below it. This line is now in true length.
3. Rotate the line in true length so that it is perpendicular to the folding line
4. Transfer the new point to the opposite view to get the point view of the line.

You can now measure the distance between the two points.

Here is an example problem: (the method to solving this problem is underneath)

Example One: Finding the Shortest Distance Between a Point and a Line The red lines indicate the next step in the image.

1. Step A/B ) Rotate the line in one of the views (of your choice, in the example, the top view is used ), so that the line is parallel to the folding line.
2. Step C ) Transfer the new point to the other view below it. This line is now in true length.
3. Step D ) Rotate the line in true length so that it is perpendicular to the folding line
4. Step E ) Transfer the new point to the opposite view to get the point view of the line.
5. You can now measure the distance between the two points.

Here is the solution:

Finding the Shortest Distance Between a Point and a Plane:

1. Choose one side of the plane to rotate into true length. You will use this line to rotate for the rest of the problem. In this example bottom line of the plane is used.
2. Rotate this line in one of the views (of your choice, here the top view is used), so that the line is parallel to the folding line. Rotate the last point over as well. (See Rotating a Plane for further instructions).
3. Transfer the two new points to the other view below it. This line is now in true length.
4. Rotate the line that is in true length so that it is perpendicular to the folding line so that you can find the plane in edge view.
5. Transfer the new point to the opposite view to get the point view of the line.

You can now measure the distance between the two points. Please note, when measuring from the point to the plane in edge view, the line of measurement must be perpendicular to the plane in edge view. Otherwise you will not be able to find the shortest distance.

Here is an example problem: (the method to solving this problem is underneath)

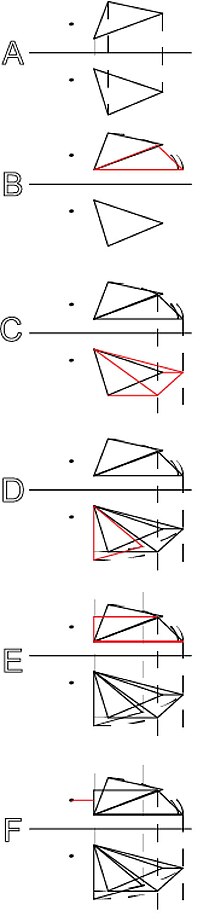
Example Two: Finding the Shortest Distance Between a Point and a Plane The red lines indicate the next step in the image.

1. Step A ) Choose one side of the plane to rotate into true length. You will use this line to rotate for the rest of the problem. In this example bottom line of the plane is used.
2. Step B ) Rotate this line in one of the views (of your choice, here the top view is used), so that the line is parallel to the folding line. Rotate the last point over as well. (See Rotating a Plane for further instructions).
3. Step C ) Transfer the two new points to the other view below it. This line is now in true length.
4. Step D ) Rotate the line that is in true length so that it is perpendicular to the folding line so that you can find the plane in edge view.
5. Step E ) Transfer the new point to the opposite view to get the point view of the line.
6. Step F ) You can now measure the distance between the two points. Please note, when measuring from the point to the plane in edge view, the line of measurement must be perpendicular to the plane in edge view. Otherwise you will not be able to find the shortest distance.

Here is the solution: