Descriptive Geometry/Cone Loci
Definition
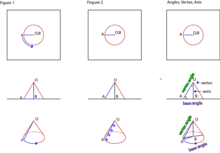
editA locus(loci) is a solution(s) that satisfy a given set of conditions. [[[[Media:|thumbnail]]]] Depending on the situation, the locus can be a different solution. In Figure A, there is a vertical axis BO and a point a. When point a is revolved around BO, the path that point a creates is a circle. In this given set of conditions, the locus is the circular path that point a creates when revolved around BO because that circle is a collection of all the points that are the same distance from BO as point a. In Figure B, there is a vertical axis BO with a line segment AO touches BO to creates ∠AOB. When AO is revolved around BO, the path that the AO creates a surface that takes the shape of a cone. Therefore, in this particular set of conditions, the locus AO is a conical surface because that surface is a collection of all the line segments that can be represented by AO in a three-dimensional space.
The locus of two intersecting objects would be all the solutions that satisfy the intersection. In the case if cone "A" and cone "B" shared a vertex and had the same slant height, there are three possible solutions: 1 intersection, 2 intersections, or none. If the angle between the two axis is less than the sum of the two vertex angles, there are two locus intersection solutions. If the angle between the two axis is equal to the sum of the two vertex angles, there is only one solution. If the angle between the two axis is greater than the sum of the two vertex angles, there are no solutions.
Solving Cone-Loci Intersections
editConsider top and front views of two intersecting lines AO and BO with an angle of ∠AOB as given. The vertex angles formed by the line revolved around AO and BO(creating cones) are α and β respectively. Construct the views so that one view shows both the cone axis in true length (front) and the other in point view (top). In the true length view, construct a circle of arbitrary radius so that it intersects with the slant heights of the cones. Connect the intersections of the cone and the circle to create the bases of the cones. Mark all the points that each base of the cone intersects with another cone base. These are your loci of the cone intersections. The lines formed from the loci to the vertex are the edges in which each cone meets its neighboring cone.
If the axes of the cones are not segments, but infinitely long lines, it is necessary to test if there are more two solutions. The rotating line that creates the conic surface can point in different directions from the vertex, creating a possibility of two cones. Because of this, there can be a maximum of four loci intersections for four cones.
-
Descriptive Geometry Cone Loci Problem 1
-
Descriptive Geometry Cone Loci Solution 1
-
Descriptive Geometry Cone Loci Solution 2
-
Descriptive Geometry Cone Loci Problem 2