Circuit Theory/Convolution Integral/Examples/example49/VL

Given that the source voltage is (2t-3t²), find voltage across the resistor.

series LRC circuit ... find voltage across the resistor

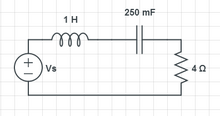
This is the V_L solution.

Outline:

Transfer Function

$H(s)={\frac {V_{L}}{V_{S}}}={\frac {s}{4+s+{\frac {1}{0.25s}}}}$

simplify(s/(4 + s + 1/(0.25*s)))

$H(s)={\frac {s^{2}}{s^{2}+4s+4}}$

Homogeneous Solution

solve(s^2 + 4.0*s + 4.0,s)

There are two equal roots at s = -2, so the solution has the form:

$V_{L_{h}}(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

Particular Solution

After a long time attached to a unit step function source, the inductor has shorted and the capacitor has opened. All the drop is across the capacitor.

$V_{L_{p}}=0$

This also means that C₁ has to be zero.

Initial Conditions

So far the full equation is:

$V_{L}(t)=Ae^{-2t}+Bte^{-2t}$

Initial voltage is all across the inductor.

$V_{L}(0)=1=A$

$A=1$

At this point will have to do integral .. to get to the current. There is no other way to use the known initial conditions: current (initially zero), and V_C (initially zero). Will have to introduce integration constant and then evaluate that. More chance of mistakes, more complex, so start over with something else.

$i(t)={\frac {1}{L}}\int _{0}^{t}V_{L}(t)dt=\int _{0}^{t}(e^{-2x}-B(x)e^{-2x})dx$

f := (exp(-2*x) - B*x*exp(-2*x));
S :=int(f,x=0..t)

$i(t)=B*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}}+C_{1}$

$i(0)=0=C_{1}$

Ok so C₁ is zero. Now need to find B. Find B by doing another integral to get V_C:

$V_{C}(t)={\frac {1}{C}}\int _{0}^{t}i(t)dt=4*\int _{0}^{t}(B*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}})dx$

f := (4*(B*(exp(-2*x)*(2*x+1)/4 -1/4) - exp(-2*x)/2 + 1/2));
S :=int(f,x=0..t)

$V_{C}(t)=B+2t+e^{-2t}-Bt-Be^{-2t}-Bte^{-2t}-1+C_{1}$

$V_{C}(0)=0=B+1-B-1+C_{1}$

$C_{1}=0$

Still doesn't help us find B. Guess B = 2 since (2t-Bt) has to equal zero if V_C is going to converge on 1. Then see if V_C(∞) = 1:

$V_{C}(t)=2+e^{-2t}-2e^{-2t}-2te^{-2t}-1$

At t = ∞ what is the 2te^-2t term's value?

limit(B*t*exp(-t),t = infinity)

Mupad says 0.

$V_{C}(\infty )=2-1=1$

Yes! B = 2 works ... looks like the only thing that works .... So:

$i(t)=2*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}}=te^{-2t}$

simplify(2*(exp(-2*t)(2*t+1)/4-1/4) - exp(-2*t)/2 + 1/2)

This means that V_R is:

$V_{R}(t)=4*i(t)=4te^{-2t}$

Impulse Solution

Taking the derivative of the above get:

$V_{R}\delta (t)=4e^{-2t}-8te^{-2t}$

Convolution Integral

$V_{R}(t)=\int _{0}^{t}(4e^{-2(t-x)}-8(t-x)e^{-2(t-x)})(2x-3x^{2})dx$

f := (4*exp(-2*(t-x)) - 8*(t-x)exp(-2*(t-x)))*(2*x-3*x^2);
S :=int(f,x=0..t)

$V_{R}(t)=8-8e^{-2t}-10te^{-2t}-6t$

There will not be any constant since again, V_R(t) = 0 after a long time ... and the capacitor opens.