Calculus/Extrema and Points of Inflection

← L'Hôpital's rule	Calculus	Newton's Method →
	Extrema and Points of Inflection

Maxima and minima are points where a function reaches a highest or lowest value, respectively. There are two kinds of extrema (a word meaning maximum or minimum): global and local, sometimes referred to as "absolute" and "relative", respectively. A global maximum is a point that takes the largest value on the entire range of the function, while a global minimum is the point that takes the smallest value on the range of the function. On the other hand, local extrema are the largest or smallest values of the function in the immediate vicinity.

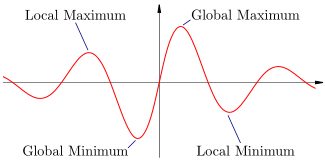
In many cases, extrema look like the crest of a hill or the bottom of a bowl on a graph of the function. A global extremum is always a local extremum too, because it is the largest or smallest value on the entire range of the function, and therefore also its vicinity. It is also possible to have a function with no extrema, global or local: $y=x$ is a simple example.

At any extremum, the slope of the graph is necessarily 0 (or is undefined, as in the case of $-|x|$ ), as the graph must stop rising or falling at an extremum, and begin to head in the opposite direction. Because of this, extrema are also commonly called stationary points or turning points. Therefore, the first derivative of a function is equal to 0 at extrema. If the graph has one or more of these stationary points, these may be found by setting the first derivative equal to 0 and finding the roots of the resulting equation.

However, a slope of zero does not guarantee a maximum or minimum: there is a third class of stationary point called a saddle point. Consider the function

f(x)=x^{3}

The derivative is

f'(x)=3x^{2}

The slope at $x=0$ is 0. We have a slope of 0, but while this makes it a stationary point, this doesn't mean that it is a maximum or minimum. Looking at the graph of the function you will see that $x=0$ is neither, it's just a spot at which the function flattens out. True extrema require a sign change in the first derivative. This makes sense - you have to rise (positive slope) to and fall (negative slope) from a maximum. In between rising and falling, on a smooth curve, there will be a point of zero slope - the maximum. A minimum would exhibit similar properties, just in reverse.

This leads to a simple method to classify a stationary point - plug x values slightly left and right into the derivative of the function. If the results have opposite signs then it is a true maximum/minimum. You can also use these slopes to figure out if it is a maximum or a minimum: the left side slope will be positive for a maximum and negative for a minimum. However, you must exercise caution with this method, as, if you pick a point too far from the extremum, you could take it on the far side of another extremum and incorrectly classify the point.

The Extremum Test

A more rigorous method to classify a stationary point is called the extremum test, or 2nd Derivative Test. As we mentioned before, the sign of the first derivative must change for a stationary point to be a true extremum. Now, the second derivative of the function tells us the rate of change of the first derivative. It therefore follows that if the second derivative is positive at the stationary point, then the gradient is increasing. The fact that it is a stationary point in the first place means that this can only be a minimum. Conversely, if the second derivative is negative at that point, then it is a maximum.

Now, if the second derivative is 0, we have a problem. It could be a point of inflexion, or it could still be an extremum. Examples of each of these cases are below - all have a second derivative equal to 0 at the stationary point in question:

$y=x^{3}$ has a point of inflexion at $x=0$
$y=x^{4}$ has a minimum at $x=0$
$y=-x^{4}$ has a maximum at $x=0$

However, this is not an insoluble problem. What we must do is continue to differentiate until we get, at the $(n+1)$ th derivative, a non-zero result at the stationary point:

f'(x)=0\ ,\ f''(x)=0\ ,\ \ldots \ ,\ f^{(n)}(x)=0\ ,\ f^{(n+1)}(x)\neq 0

If $n$ is odd, then the stationary point is a true extremum. If the $(n+1)$ th derivative is positive, it is a minimum; if the $(n+1)$ th derivative is negative, it is a maximum. If $n$ is even, then the stationary point is a point of inflexion.

As an example, let us consider the function

f(x)=-x^{4}

We now differentiate until we get a non-zero result at the stationary point at $x=0$ (assume we have already found this point as usual):

f'(x)=-4x^{3}

f''(x)=-12x^{2}

f'''(x)=-24x

f^{(4)}(x)=-24

Therefore, $n+1$ is 4, so $n$ is 3. This is odd, and the fourth derivative is negative, so we have a maximum. Note that none of the methods given can tell you if this is a global extremum or just a local one. To do this, you would have to set the function equal to the height of the extremum and look for other roots.

Critical Points

Critical points are the points where a function's derivative is 0 or not defined. Suppose we are interested in finding the maximum or minimum on given closed interval of a function that is continuous on that interval. The extreme values of the function on that interval will be at one or more of the critical points and/or at one or both of the endpoints. We can prove this by contradiction. Suppose that the function $f(x)$ has maximum at a point $x=c$ in the interval $(a,b)$ where the derivative of the function is defined and not $0$ . If the derivative is positive, then $x$ values slightly greater than $c$ will cause the function to increase. Since $c$ is not an endpoint, at least some of these values are in $[a,b]$ . But this contradicts the assumption that $f(c)$ is the maximum of $f(x)$ for $x$ in $[a,b]$ . Similarly, if the derivative is negative, then $x$ values slightly less than $c$ will cause the function to increase. Since $c$ is not an endpoint, at least some of these values are in $[a,b]$ . This contradicts the assumption that $f(c)$ is the maximum of $f(x)$ for $x$ in $[a,b]$ . A similar argument could be made for the minimum.

Example 1

Consider the function $f(x)=x$ on the interval $[-1,1]$ . The unrestricted function $f(x)=x$ has no maximum or minimum. On the interval $[-1,1]$ , however, it is obvious that the minimum will be $-1$ , which occurs at $=-1$ and the maximum will be $1$ , which occurs at $x=1$ . Since there are no critical points ( $f'(x)$ exists and equals $1$ everywhere), the extreme values must occur at the endpoints.

Example 2

Find the maximum and minimum of the function $f(x)=x^{3}-2x^{2}-5x+6$ on the interval $[-3,3]$ .
First start by finding the roots of the function derivative: