CLEP College Algebra/Printable version
| This is the print version of CLEP College Algebra You won't see this message or any elements not part of the book's content when you print or preview this page. |
The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at
https://en.wikibooks.org/wiki/CLEP_College_Algebra
Algebraic Operations
Addition, subtraction, multiplication, division, exponentiation, rationalization, simplification, etcetera. If you knew about four of these terms, you would have most likely understood the definitions of the first four. This is because you have most likely been trained very well to understand the first four terms in your elementary/primary school years. Some of these are simply extensions of those ideas.
Nevertheless, any good algebra textbook will cover the basic algebraic operations and properties of numbers. This is true because math is simply rules, in that you start with a basic set of rules so that you may operate and simplify — to be put into its most compact form — any expression — a written form of combined symbols that uses one of the two basic operations, addition and multiplication. To make sure you are not confused, here is an example:
|
Example 0.1.a: Operate this expression: . Algebra has never been more simple. This problem comes from a second grade class. In fact, many of you could probably this in your head (given the simple numbers). However, is it not strange to you that you know what you need to do once you see this expression? You add 10 to 20. Then, you subtract 5 from that resultant sum: The truth is, you have been brainwashed, conditioned to follow the rules. We wonder how many would think to do this: |
As should be obvious, you get the same answer. But why? That is what this chapter of the textbook seeks to explain.
Basic Operations of Real Numbers
editIntroduction to the Real Numbers
editAlong with that question, there is another: "what is a real number?" Before we get to that definition, we need to go ahead and go through all the systems that we worked with since primary school.
First, the natural numbers — the counting numbers or the numbers used when counting items of a set, not including zero. Then, the introduction of zero along with the natural numbers gives the full definition of the positive integers. It seems all is true until you learn about the negative integers . The full set of integers is both the positive and negative integers.
This is where the strange stuff really begins. Notice we have yet to talk about fractions, until now. The numbers in which a fraction , where is or is not divisible by , is considered rational. A rational number is simply the ratio between two numbers. By contrast, an irrational number is a number that cannot be denoted exactly by the ratio of two numbers. Later, after the introduction, you will get to see one proof of irrationality. However, a thorough grasp of algebra and real numbers is necessary to understand the proof. You will be able to do that later.
There are some restrictions on rational numbers however, some of which are situational, some of which are not, whereby the number is either an integer or results in a number that is undefined. On top of the numerator being divisible by the denominator, the following restrictions apply:
- The denominator is either or when the numerator is an integer. This should be a fact everyone knows: dividing any integer by gives the same integer again. Dividing by a negative number gives you a negative number. In dividing by , given the numerator is an integer, you get the negative version of the numerator. Either way, so long as the numerator is an integer, when dividing by or , the result is an integer.
- The denominator is for any rational numerator . For any rational numerator , dividing by zero is never a good thing (in the "real" world). We will get into why after the first section. For now, keep in mind that this is simply impossible to define using numbers that we will talk about here.
- The numerator is when rational denominator . Like the above point, this small factoid will be proven rigorously later after section 1.
Most textbooks define a rational number as the quotient of two integers, and we are no different. Therefore, we cannot say that is not an integer until we make it a quotient of two integers: Here is how we would that problem:
|
Example 1.1.a: Determine whether the following quotient is an integer: Most of you probably already know that and . Therefore, let us put it into this form:
Dividing a fraction by another fraction can be expressed the same way like so: From here, most students know what to do: eep the first fraction the same, hange the division to multiplication, and lip the second fraction (take the reciprocal). From here, multiply the two fractions (multiply the top bits together and do the same for the bottom bit) to find this:
|
Note: In case you have not seen , this is a shorthand for "Quod Erot Demonstrandum," which literally translates from latin to "that which has been demonstrated" true. This is simply mathematician code-speak for "we have finished proving everything and left no unfinished business."

The real numbers include all the sets we talked about in this section. That means it includes the integers, the rational numbers, and the irrational numbers. The following image to the left denotes the sets that will be relevant to your studies for now.
Note the symbols used to denote the specific set.
- Integers: . Putting a positive or negative superscript (e.g. positive superscript ) denotes positive or negative integers. The Z comes from ganze Zahlen, which literally translates to whole numbers.
- Rational numbers: , for quotient.
- Real Numbers: .
A quick note about notation: Normally, a mathematician will want to know what type of variables he is working with. On the CLEP exam, it is explicitly stated that the variable you are working with on specific problems are real unless otherwise denoted, as is written here: "Unless otherwise specified, the domain of any function is assumed to be the set of all real numbers for which is a real number." In symbolic terms, "belongs to the set of" is denoted by . Therefore, given represents the real numbers, you can define such that . This notation is not needed for the exam; however, it can be helpful to be quick when working with problems. To make sure you fully understand which numbers belong to which, let us look at an example:
|
Example 1.1.b: Determine each of the following as either an integer or rational number: (a) (a) First, ask, is an integer. Well, if you divide two integers only to suddenly get something beyond a decimal point, then it is not an integer and by definition becomes a rational number. Since the number is not an integer, and the number forms a decimal, then it must be the case that it was divided by two numbers and thus formulated a quotient: . We have sufficiently established this number as a rational number (although not rigourously): .
(b) has no decimals, and can be written in the form . This must be an integer: . (c) Just because it is fraction does not automatically make it a rational number. Remember, if can divide , the numerator of the fraction, it would automatically make it an integer. Notice we are not saying that the denominator has a factor to the numerator or that the denominator divides into the numerator. Rather, you can easily divide the numerator by the denominator. This is why it must be an integer: . (d) Because "4" cannot easily divide into the numerator, "5," the fraction is a rational number: . |
Of course, each example above is defined as a real number and a rational number. Regardless, it is important to understand when a qualification limits the ability to define variables accordingly. Often times, the restrictions are out in the open so that no one is confused on what the number can or cannot be.
It is now your turn to try this out. This WikiBooks uses explorations to not only help cement concepts but also challenge readers to think like mathematicians. Problems in mathematics are not always simple, and at times, mathematicians need to generalize findings for everyone so that it can be made applicable in the abstract and the concrete as well. Nevertheless, it is now your turn, so try it out.
(a)
(b) , where
(b) At the moment, you cannot determine to be part of the set of rational numbers until we make sure . Because , set , where and . Assume is coprime, meaning ( does not divide ). Knowing , the following is true:
Simplifying the fraction to be in the form , you get . There are two cases for this situation.
- CASE 1: , meaning .
- CASE 2: . Knowing , let , where . Because , .
If CASE 1 is true, then . Given this is a possibility, . If CASE 2 is true, then this definition for the fraction is still true because is a subset of . Because the question is asking for the most specific one, this is the best answer one could give.
(c) Because and , , assuming .Now that we have thoroughly introduced the reader into the land of real numbers, it is now time to find its properties.
The Most Fundamental Definitions of Real Numbers
editRecall the introduction of this chapter in which we mention a fundamental principal of mathematics:
[M]ath is simply rules, in that you start with a basic set of rules so that you may operate and simplify... any expression — a written form of combined symbols that uses one of the two basic operations, addition and multiplication.
How come there are only two basic operations? After all, there exists subtraction and division! Notice, however, what we did in Example 1.1.a. The expression has a minus sign in front of the "5," yet there is a way to rewrite the expression:. Our quandary at the beginning of the paragraph seems to now make sense. We defined these operations. If we say there are only two basic operations, then it is so. Subtraction and division are referred to as inverse operations in that they are the same as addition and multiplication with the only difference being a sign. To denote this, we will be using variables, which are symbols that denote a number that can be input such that it follows a restriction, if any exists. If you never got used to this idea in Algebra I and II, we will be introducing them slowly. Right now, get used to the idea that these are simply symbols that denote a possible real number.
- Inverse Definition of Addition: is materially equivalent to .
- Inverse Definition of Multiplication: is materially equivalent to , where .
Because the above symbols are variables, and the above operations are by definition true, any number can be input. An example should help cement these definitions in your mind. In the table below, inputs and are given on the respective column. The output of and are given. Notice that and are identical.
This table should help the student unfamiliar with working with variables get an intuitive sense of the meaning. Note, the final row is a "rule" that gives the pattern for the number. Finally, one last definition should be established before moving.
If given expression , the term .
All that the above text says is that is the same thing as . For example, . Now that you understand the most fundamental definitions of the real numbers, we can keep deriving new information from our definitions.
Closed Door Policy of Real Numbers
editLet us go back to the set of integers. If we add any two integers, , you get an integer as a result. Similar, multiplying any two integers, , gives another integer. However, if you divide two unique integers, , you will not always get an integer. For example, , which is not an integer. We would say the following is true:
- Under addition, subtraction, and multiplication, the set of integers are closed.
By closed, we mean to say that the set of integers using that specific operation will always give another integer. Similar to integers, real numbers are also closed. The following definition below tells us the most common form:
Under the operation of addition, subtraction, multiplication, and division (excluding denominator 0), the use of the operation to any real numbers is closed.
This is a simple but powerful tool to remember in the mathematical lexicon. This fact is so fundamental, in fact, that it can be used to prove a number is or is not an integer, or rational number, or a real number. To prove a number does or does not belong to a given set, you must show that it can or cannot belong to that set using those rules. We defined those operations, so you must show that a number is not defined under those axioms (definitions).
This idea is key to doing proofs in mathematics, so it is best we introduce the concept now. Also, proving a number is an integer is a very important concept in number theory. You thought you knew everything about integers? Try number theory (after learning as much as you can about Algebra) to find out how wrong you are!
The Laws of Real Numbers (Under Equality)
editNumbers are a society. They follow rules that were dictated by a ruler. In this instance, the ruler is humans. We did not discover "4," we only said that there are 4 things. Numbers are adjectives, not nouns, so by definition, they cannot be discovered. As such, everything we have talked about so far is only definitions. Keep in mind that some things are extensions of the definitions we made. However, humans have been applying these definitions for so long that we were able to "discover" new facts about mathematics. We will see the discoveries in the second section. However, for now, let us define the rules that humans have used for hundreds of years now!
For all real numbers , , and , . That is, the grouping of real numbers does not change the sum.
It turns out proving this is true takes a lot more than basic algebra. Unfortunately, for the curious student, it is hard to explain these simply. If you want to prove these are true, you will want to do abstract algebra. In fact, the three definitions below cannot be simply proven (or at least shown) with either algebra or geometry, so simply accept these as true for now.
For all real numbers and , . That is, the order of addition does not matter.
For all real numbers , , and , . That is, the grouping by which three numbers are multiplied does not change the product.
For all real numbers and , .
For all real numbers , , and , .
As a convention in this book, we will outline all proofs that we can present in the green boxes below. This should hopefully make the later examples more manageable to students (since a large part of this textbook will be to help students see that math is not about memorization but discovery). Plus, for students that have no interest in them (even though they should), it can be skipped. However, we do not recommend this approach unless you are only here to memorize facts, which may not make math fun for you. hould make proofs easy to find. Plus, for students that have no interest in them (even though they should), it can be skipped. We hope that the language we will use will allow students to engage in these proofs with little to no hesitation!s
For now, we will accept that the distributive law is true for all real numbers.
We have two more properties to define before we move on. Notice how they are in different sections. There is a reason for that, as you will see with the zero factor property and the identity elements.
For all real numbers and , if and only if or or and . In other words, for all real numbers and , if and only if at least one of the factors is zero.
Say that we have found out that the following equation below is true:
The scary looking equation aside, use some basic logic so that the answer shall be easy to find. For the expression to be true, it needs to be the case that either or or both. If at least one of the factors is zero, then the expression will always be zero. This is simply another definition of mathematics that we humans have used for many years now. If you want to solve such an equation, wait for it. If you can already, go ahead. Otherwise, keep reading.
For all real numbers , the following are always true:
- . When adding by , you get the same real number .
- . When multiplying by , you get the same real number .
When you hear "identity," you think of a person's name. In math, however, identity simply means a number that does not change another number. What number makes that true? Let us some basic logic to figure this out.
- What number makes it so that by adding it to another you get the same number? If a result does not change, that logically means the difference is zero because if there exists absolutely no change, then the difference between the overall output and the initial input is zero. As such, for any real number , the identity element must be , or .
- What number makes it so that by multiplying it to another you get the same number? We can use the exact same logic to find the number we are looking for. If we are multiplying a result, we want some way to find the overall change when multiplying. In this instance, division would work. Excluding from the real numbers, . Can we say that multiplying by 1 gives the same number? Yes, , so the identity element is true for all real numbers.
If for the real numbers , , and , , and , then .
This is simply true by definition. For example, if , and , then .
Check Your Understanding
editIt is always a good idea to test your knowledge, to see if you truly understand. However, it can often be difficult to test yourself when you cannot think of any problems to do. As such, here are some problems that relate all the knowledge you learned.
Part A
editInstructions: without using a calculator, find a way to calculate these expressions below in under 1 minute and 30 seconds. For each "text box," write the number that makes the value true. Do not write commas in the boxes because those are interpreted as decimals.
Part B
editInstructions: In under 2 minutes, without using a calculator, answer each question below.
More will be added later
Introduction to Algebra
editYou may have saw the algebra required part of the check your understanding and may have wanted to give up. "When did math introduce letters anyway; it is already hard enough as it is!" Well, there should not be any need to worry because is easy once you understand the core principles behind it (that is, until you get to modern [abstract] algebra). The most fundamental of those rules is outlined below:
When given an equation – expressions set to equality or inequality – the opposing sides must be equal to each other, or at least one of the expressions is either lesser than or greater than the other.
Is ? Yes, it is. We know the operation must be an equation, because it is true to what it states, that adding two things with two things is the same as four things. However, what happens when you introduce variables – objects that introduce a source of change to an equation. If one side is equal to the other, then the variable of interest must be equal to some expression so that it operates with the other variables or non-variables such that it equals the other side. Look at the example below to see what we mean:
The value of must equal some constant number to make the above equation true; otherwise, the expression cannot be equal. If put into a sentence, the above equation is asking us to "find the value of that makes it so that multiplying it by 5 and adding 2 gives 17." In the very early days of math, it used to be the case that questions were asked in such a fashion. Algebra makes these problems easier (both in the statement of it and in the evaluation of it). In this section, we will discuss how to solve single-variable equations and multi-variable equations. Then, we will determine how to find the value of variables when given a system of equations.
Simplifying the Complicated
editBefore we do that cool stuff, however, it is important the student has a grasp on the anatomy of equations. The first idea students learn is "term":
The term is a single mathematical expression that is either a single number (a constant), a single variable, multiplied variables, or variable(s) multiplied by constants, each separated by a plus () or fraction sign ().
For example, look at the following expression: . There are two terms according to the definition above: and . is a variable multiplied by a constant, which is also similar to . The two terms are separated by a plus sign. Combining terms make up the expression. The equation is equality or inequality of two expressions. This forms the basic anatomy of the equation and the expression. Sometimes, however, there are more terms than needed in the expression. The procedure during such times is to simplify the equation or expression.
The act of simplifying equations (or expressions) is one whereby "like-terms" are condensed and combined, without changing the equation's equality or inequality illegally.
Before we keep refining the above definition (e.g. what are "like-terms"?), it is important to get an example of this. Some equations or expressions that are not simplified are provided below:
The bullet points below correspond to the equivalent unsimplified expressions above, in the order given.
Making things simpler is usually what you want to do in math problems, and this is especially true in College Algebra, because the act of making things simpler is inherent to finding the one value of the variable of interest to make the equation true. Despite the very simple act of simplifying equations, students may make some common errors because there is no definite idea of "like terms." It is important to get this idea correct before moving on to like-terms. As such, the definition and examples are provided below.
Like-terms are two terms that are either constants or have the same variables with the same exponents (values that denote the number of times a term is multiplied by the same number).
The above definition is one of the better ones; however, it can be a little confusing to students. Therefore, an exploration is in order. Imagine the following expression below:
This expression above is quite messy, so let us see if we can simplify the above expression. First, let us look for terms that have the same variables with exponents within them. Those that are "alike" will be highlighted in their corresponding color.
Notice how negatives are highlighted. This is because it is separated by the plus sign, for . As such, those are different terms. Notice how and are "unlike" terms. This is because is missing the variable . Because it does not have the same variable, those two are unlike terms. The next procedure would be to rewrite the above equation like so:
To combine the above terms, simply combine the constant values or the constant values corresponding to the like terms. This is true because the constant values next to those corresponding constant values can be factored. For example, , where the variable is multiplied to the corresponding constant values. From this property, the idea of combining like-terms make sense.
As long as the variables multiplied to the constants are exactly alike, where each variable is identical along with the exponent value, the two terms can be combined due to factoring allowing the corresponding constants to be added.
This is the most important principle behind factoring, and should be rigorous enough such that any mathematician (and student) can agree that the definition of "like-term" makes sense. Enough fo that, it is time to finish the problem we have stated. Keeping the colors for the like terms, we yield:
This answer above is the simplest form available for this above expression. Keep in mind that the simplest form is a little subjective, and it is based on what the question is asking, so there is no true definitive way to determine "simplest form." The best one can do is infer whether that form is the easiest one can use. For the above expression, it could be the case that this may not be the simplest, but this is due to notation (which we will get into more detail in Binomial Theorem). If you are curious to see the simplest form, which you may not understand at this point in time, here it is:
One other thing about simplifying equations is a little warning. An expression is provided, and a few students got different answers. Your job is to determine who is correct (and yes, these are your exploration).
However, each person got a different answer. Determine which person got the correct answer, and explain your choice.
(A)
(B)
(C)
(D)
Alternatively, you may have noticed the definition said that "Like-terms are two terms that are either constants or have the same variables with the same exponents" (emphasis added). Because have the same variables, and , those two can be combined. Given the same cannot be said for the other variables, the only answer that can be true is (E).
Should you get the above exploration, you basically understand the idea of simplifying equations and maybe the associate property of multiplication. Either way, good job if you got that one correct.
However, each person got a different answer. Determine which person got the correct answer, and explain your choice.
(A)
(B)
(C)
(D)
.
As such, is the result. Combining all "like terms," you get
The above explorations may be how the CLEP exam may try to trick you into picking the wrong answer. It is because each answer choice may be a common mistake a student will make when trying to simplify an expression. These are usually the first questions of the test, so it may be best not to get those wrong because of an embarrassing mistake like not distributing the negative 4 to all terms or forgetting about the negative number in the first place.
Solving for One Variable in An Equation
editThe level of detail we will go into here may seem excessive. However, this magnification will be necessary to explain why we are certain some things work they way they work. Plus, some students appreciate when questions are answered that they would likely ask. As such, bear with us as we demolish through these simple problems. As another bonus, you will understand algebra more than current students taking the College Algebra class in university, so you should look at this as a blessing. The blessing comes in this encompassing principle:
For an equation that has a variable, the variable is only true when going backwards. That is, using inverse operations, the operation on the other side is now transferred to the other side without the variable.
This basic property is what allows us to solve for equations. After all, since both sides change by the same amount, there should be no discrepancy between the equality signs. This gives us the basic definitions below:
If , and , then
If , and , then
If , and , then
If , and , then
These properties above, along with the properties of real numbers listed in the previous section, will be very helpful when trying to solve equations. We will be stating these properties as we work through them in the examples that follow. Therefore, it is a good idea to understand how we present our work and incorporate that style into your work for the exploration. Although this may be a multiple choice test, if a student moves on to a higher math, then it is important to know how to communicate mathematically, especially on paper.
The process of isolating the variable of interest is such that on one side only, the variable of interest has no constants added or multiplied to it, except for 0 and 1, respectively, and the variable is equal to a constant or expression with the variable of interest not on the other side.
The above statement can be a little confusing if one has not seen an example of this procedure, so two examples are given below, one with only one variable and one with multiple variables. From there, the examples will present a more concise procedure.
|
Example 2.2.a: Find the value of that makes the equation true: . From here on out, because whatever is true on one side is also true of the other, we will no longer be stating that the two sides are equal. However, keep this in mind every time you are solving equations, because if both sides must equal, then what is done one side must be done to the other to make them equal! We will step you through the process so that one can see how to isolate the variable of interest. The equation in the problem is rewritten below: Add to both sides of the equation. The effect of adding is to make it so that the left side of the equation is adding the identity element to . Because the identity element does not change the left side, we may safely ignore it. Because is multiplied to the variable , to make it so that is not changed, multiply to both sides of the equation. The effect of multiplying is to make it so that the left side of the equation is multiplying the identity element to . |
We know this makes the equation true because when isolating the variable, we made sure the equation always remained the same. This process ensured that the value of will always give the right number. Nevertheless, if you do not feel confident about the work you did, a good way to double check your answer is to "plug it in" and see if it holds true. Here is how one would do it:
If the expression on one side, after being operated, gives the same result as the expression on the other side, then the value for the variable, , you found must be true so that it satisfies the equation. Unfortunately, sometimes, on the CLEP exam, you may not always be given one-variable equations. There may be times when you are given more than one variable. The same procedure applies for what we did above, except this time, you must be extra sure of yourself that the answer you have is definitely correct, for although you may substitute the answer you got into the equation, this one may be a bit more tedious.
It is given that we will keep stepping through the process for you. After all, the student that is not familiar with working with equations tends to get lost if not stepped through. Plus, for the student that understands the algebra, it helps to see problems so that one can see how to work them through step-by-step. Mind you, these steps are not meant to be efficient. For now, think of these as little problems that set up the big bad later on.
|
Example 2.2.b: Find the value of that makes the equation true: . The first step when doing any problem is to not panic. Do not get too bogged down with the details; simply fight for your answer. Of course, the CLEP exam is multiple choice, although it is a good idea to learn how to do these problems without relying heavily on multiple choice tricks. Tricks should only be a last resort for problems that you have no idea how to work out during the short amount of time you have to think. This problem is way easier than it may seem at first, and using tricks on it may be slower than not using them and doing it the straight way. Realize that the same philosophy we had when working with problems is the same: whatever is done to one side, you do on the other as well. Before we begin, let us write down the equation again: Let us begin by adding to both sides of the equation. This will eliminate the constant term on the right hand side and move it over to the other side. The effect of adding is to make it so that the left side of the equation is adding the identity element to Next, eliminate the fractional term multiplied to the variable of interest. Here, we will be a little slow and work it through one at at time before we introduce a neat consequence of the slow working we have done here. For now, think it through this way. If we want to get rid of something that is divided, we want to work with the inverse operation. Therefore, we need to multiply the fractional term. First, let us rewrite what we see so far into something simple:
Doing this is equivalent because we know that . Because multiplication is commutative, we understand that the terms can be multiplied in any way we want. Plus, because we know that multiplication is also associative, we know grouping does not affect multiplication. Therefore, we may rewrite the following expression like so: . It is worth your time understanding all the steps underlying the above indented line. All we did is simply eliminate the parentheses that are unnecessary, moved some terms around, then added the parentheses back in. You can think of these parentheses as denoting the numerator of the fraction. Either way, we know the above expression is equal to , so what we do on one side must be done to the other. To get rid of the division, we must multiply, as shown below.
Notice the parenthesis around . This is important, because we are multiplying this entire term by . We will explain in full detail why this is important later, but for now. Let us continue. Notice we are nearly done isolating the variable . To complete the step, we must transfer to the other side. As such, do the inverse operation. The inverse operation of multiplication is division. As such, multiply both sides by :
|
We know some readers might be asking why we did not divide this weird symbol (capital Delta) from . For one, the question is asking for , but also, may be an important abbreviation for something: the change in . The equation may look a little bit more messy having to define to different and and . In the interest of not confusing a lot of scientists, specifically, you write delta to denote a change in the variable of interest. This is how it works, so it may as well be a good idea to be exposed to this notation. If we were to redefine the above equation without any , then we would write the following:
- , which simplifies to . You could see why is very popular in science.
One of the more strange aspects of the problem come with the parentheses. We asked why we put parentheses around items but not around . The first one is easier to explain than the second, so we will begin with the easier one.
- Any term that is finite will effectively equal something. Wen adding terms, such as , it must equal some other term, say . When multiplying the entire expression by a term , you are effectively multiplying the end result, , by . If , and you are multiplying by , then . This is why, when adding terms, you must put parentheses around what you are multiplying. There is no law stating that multiplying and adding are commutative or associative (recall that it is distributive, however).
- By extension of the first premise, if is multiplied by some term, say , then if , then . Because multiplying is commutative and associative, there is no need to put parentheses are around . As such, the expression did not need parentheses.
There is trick that we can learn from the above problem. Recall how we stated that we are complicating the problem a bit with what we are doing, specifically with the fractional term. This is because we are not utilizing a common trick with fractions multiplied to a term of interest. However, the understanding of this "trick" should be necessary before we ever utilize it. Tricks are fine, but that is not what math is all about. This is what makes math boring for so many students. What is this trick?
Definition: A reciprocal is a fraction that swaps the location of the numerator and the denominator such that it forms the fraction .
Trick: When a variable of interest, say , is multiplied by a fractional term, say , such that it gives , multiplying by the reciprocal allows the variable of interest to be "isolated."
Let us unpack this slowly. A reciprocal of a fraction is effectively swapping the location of the numerator and the denominator. For example, the reciprocal of is . When you multiply by the reciprocal, what you effectively do is make it so that the following is true:
.
As such, multiplying by the reciprocal will shorten the time it takes to finish the problem. Let us see how this would have worked with the previous problem. If the following is true,
,
then multiplying by the reciprocal to both sides gives
- .
We got the same answer with very little delay. The only thing is that the answer does not look the same. However, they effectively are. If , then because of the associate property,
the same answer from the above paragraph. The long convoluted steps we took gave us the same answer! This is where the true beauty of math is found. Hiding the beauty loses out on the intricacies that took place in the above problem.
We are not saying to not remember the trick. However, we are saying to lock this reasoning in your heart. If you cannot do that, then just remember the trick because any way you can shave time of the test, the better.
The color below indicates the concise argument of the full explanation given in the answer of the example above.
|
Example 2.2.b (REPEAT): Find the value of that makes the equation true: . This example is a concise argument of the above example. Concise explanations must be given for everyone to understand what you are doing. Following along a huge line algebra can actually confuse people, so this is necessary. |
Notice how we used different letters. Always keep in mind what the question wants you to find.
|
Example 2.2.c: Solve for in the following equation given below:
This example will be explaining every step. The repeat of this example will demonstrate the more concise argument. Play close attention to the repeat so that you may be able to digest the information. At the end of each example (except the word problems and long problems which require explanations), there will be a concise solving of the multistep equations presented. Apply the subtraction property of equality so that the following is true: Simplify and combine like terms: Apply the multiplication property of equality by multiplying both sides by : Because by the symmetric property of equality,
|
The next problem will bring us back to the single-variable equation before introducing a harder variation of the single variable equation problem.
|
Example 2.2.d: Solve for in the following equation given below:
Fractions in algebra can be very tricky. That is why this is taught in a college algebra course. Knowing how to manipulate fractions will be very important when discussing rational functions. Although not its own section on the CLEP College Algebra exam, it will be very important to be able to simplify these functions so that one can easily determine its graph. Apply the property of multiplication (proven in Intro to Algebraic Proofs) that : For the next step to make sense, we need to prove one property.
From the above proof, we can finally use the multiples of base lemma (a "little" theorem used to prove what we wanted to show): Apply the distributive property within the denominator of the fraction: Apply the division property of equality by dividing both sides by : The multiplicative property of equality will be used here. Another way to do the problem will be presented after: Distribute the to : Subtract the and apply the subtractive property of equality: Finally, divide the and apply the division property of equality: Because , by the symmetric property of equality,
|
This example also has another trick that can be applied. In actuality, it is another property of equality not often in college algebra classes, and that is the following.
New property added later after new edit.
It turns out this special car can reach in 3 seconds. If you are a bit confused as to how we reached the answer, well you should be. This is a preview into modeling equations, specifically linear equations. You will see another problem like this later. However, for right now, you are finished. The most confusing part about this problem is the units. It is certainly possible many students are not exposed to physics problems like these in math class, so these students may not get this problem correct simply because of the nature of the word problem.
On a brighter note, you may be noticing a pattern with how we are solving these problems. What we are effectively doing is a "backwards order of operations." The plan was to show three examples of this in action before simply giving the answer. Simply put, the person simplifying the equation will be doing so in a manner consistent with reversing the order by which operations are to be done systematically. Before doing this procedure, make sure to simplify the equation as much as possible. The ultimate demonstration of this procedure is shown in Example 2.2.g. For now, follow along with one more word problem.
|
Example 2.2.f: Assume two blocks with masses and are attached to a pulley, where is on a wooden table with a coefficient of kinetic friction , and is suspended in the air. Assuming the system has no change in speed or direction, the following equation models the situation:
Woah, what a scary looking problem! Most of the problem's "scare factor" comes from the situation in which the equation it models comes from. Most students will want to understand what the problem is talking about first before they do the problem. However, this is not Physics – this is College Algebra, so there is no need to worry too much. We will step you through the process so that one can see how to isolate the variable of interest. The equation in the problem is rewritten below:
In case you never read a math textbook before, (1.2.2.1) denotes an equation we will be referring to later in this textbook. The decimals denote "chapter/section/subsection/order of equation reference." First things first, whatever we see is equal to another object, we will use the transitive property to make our lives easier. Case in point, and , so "plug those in" to equation 1.2.1.
Because of the associative and commutative property of multiplication, , so the equation must be equivalent to
The problem is looking for a truth about the mass suspended in the air, so isolate the variable . Before we do that, notice that is found in both terms, and , so based on the fact that both terms have a factor of , . Have the factored form rewritten below:
Because of the zero factor property, or .[Footnote 2] Because of the given situation, we will ignore to find out more about . Because of how is written, move to the other side by adding to both sides of the equation. This will make it so that the identity element on the left side is added to :
Because the identity element does not change the left side, we may safely ignore it. From here, we are done. We know that the kinetic friction , so the mass of the block suspended in the air is half of the mass of the block on the wooden table. This would most likely be the answer you would find on the multiple choice question. |
Here, we were able to use algebra to find out a truth about the system when there is no change in direction or speed. You can see why physics loves algebra, and it is for this precise reason. In fact, other fields of science love algebra as well. However, physics is perhaps the biggest lover. From our experience with equations, you may have noticed we used the properties we talked about in the beginning. If you skipped that section, or do not understand it, you are screwing yourself over. Algebra requires those fundamentals, so if you don't understand them, you must understand it now! After you finally understand those fundamental concepts, it is time to learn more about new definitions.
A single-variable equation is an equation in which only one variable of interest is shown throughout.
Examples of these equations are shown below:
Notice how the variable can be on both sides of the equation and yet still be called a single-variable equation.
A literal equation is one in which at least two unique variables are shown throughout.
Examples of these equations are shown below:
- , where pressure constant liter/mole Kelvin.
Sometimes, the CLEP exam may ask you to interpret an equation. Information is given and you will have to solve for or interpret new information based on that equation. These would be the hardest problems of the exam.
Substituting is the act of replacing a variable with a value or other expression. This is informally referred to as "plugging in" for a variable.
In Example 2.2.e, because , and and , we may substitute knowing what we know. This is how we got ().
Because we have yet to introduce an example of a single variable equation with the variable of interest on both sides, let us do the problem below.
|
Example 2.2.g: Find the value for that makes the equation true: This equation is something that is surprisingly simple to solve. We recommend you try this problem yourself before we explain how to do it, both as a test of your knowledge and as a way to check your answer.
One common student misconception that should be addressed swiftly is this: do not divide the within the parentheses. There are two reasons for this:
If dividing by is slow, then how do we do this quickly? Notice how we are dividing with another . A good way to eliminate them by moving the bottom to the other side. Because the inverse operation of division is multiplication, do that so that way the identity element is multiplied to the left hand side:
Some students may want to distribute the 20 to each term in the parentheses. While this may be fine when working with expressions, since we are working with an equation, let us make this process go faster by multiplying both sides by . This can be done because is the same as multiplying to some variable , so . As such,
Then, you can distribute the 2 to each term in the parentheses.
Now, add both sides with . This is to isolate one side with .
Because the is not isolated (you are multiplying to the ), multiply both sides by .
|
In the above example, we mentioned that it may be faster to multiply both sides by to easily solve for . Let us explore how solving for would be difficult for the below equation:
First, notice that the side with is added by , so it would be best to get rid of that constant. Add to both sides:
Notice that the above expression can be rewritten to this form: . Because every problem with a fraction can be thought of as simply multiplying, so by this very idea, one can isolate the by multiplying both sides by .
Because the reciprocal of is equal to , one could take the reciprocal of the reciprocal to both sides. That is to say, take the reciprocal of and . This would mean the solution set would be
You may not be certain doing one or the other is faster because of how the above example was framed. However, the way we did the example (boxed) is the faster way in terms of thought processing. A student intimately familiar with algebraic operations may do the above method (not in box), and may perhaps do it quickly. With the introduction of these algebraic operations, however, and presuming no intimate familiarity with algebra for the reader, we supposed it would be faster to do the boxed method.
Solving for Multiple Variables
editNotice how in Example 2.2.d, we were able to get rid of many variables by substituting information into what we know. This gave us a taste of solving multiple variables. You would be hard-pressed to find situations in which you do not need to solve for two variables. An example will perhaps be a good place to start with knowing about situations. Realize, however, that the solution will not be provided. We will be exploring the solution.
|
Example 2.3.a: A couple has a shared fund where either John or Mary will set aside part of their income to contribute to necessary payments. John is willing to set aside 52% of his income to pay for the income while Mary is willing to set aside 35% of her income to pay for the necessary expenses. If the necessary expenses make up $800 per month, while the total overall income earned by the couple is $2,150 per month, what is the minimum amount Mary must set aside so that she fulfills her promise? This is quite an interesting problem. First, we need to know how much Mary and John are making. Of course, we could ask them for more details, but let us have some fun, instead. First, let us write down what we know is true:
Since we do not know how much each is making, let us define some variables. Let represent Mary's monthly income and let represent John's monthly income. Since we know Mary and John make a combined income of $3,500 per month, the following equation below is true:
Since we know Mary and John set aside a certain percentage of their income towards monthly expenses, we know the following equation is also true:
This is all the information we have. However, how do we determine the income of Mary and John? |
This is quite the situation, and we will return to it later. However, as of right now, look at this as the challenge questions we will soon be able to solve. For now, let us work with an abstract space as opposed to the real world. Why do that? Because the real-world is messy while the abstract world follows our rules and our logic, although we must be precise with it.
|
Example 2.3.b: If and are part of the system of equations, find . Back into familiar territory once again. This problem seems a little similar to Example 2.2.d in terms of things for which we can substitute. This technique seems to work especially well in a situation like this and can make our lives especially easier. Let us bullet point the information we see in front of us into what is called a system of equations. We denote these systems using brackets on the left-hand side (usually). Sometimes, these systems can simply be denoted by writing the two equations on top of another.
Notice that this system has defined , so because it is a part of this system, we may use this information on . Before we do that, let us solve for on the first equation. We do the procedure as always. By now, you should be familiar enough with this algebraic manipulation such that you may not need us anymore. However, we will still explain some manipulations we believe need explaining. Let us begin using algebra on the first equation in the system: Recall that multiplication is commutative. Since we are trying to isolate for , the variable of interest, and is multiplied to , it is possible to divide both sides by . The justification for this is simply a matter of associativity and commutativity, which we have explained thoroughly in Example 2.2.b. Keep in mind that this associativity and commutativity allows the student to divide like the following: This type of analysis will be explored further on the next page. Regardless, this helped us solve for . Using what we know, , we may do the following to find the answer to the question: |
What we have done is solve by substitution, which is a technique whereby an isolated variable on one of the equations of the system can be used to solve for the variable of interest on the other. Keep in mind, this can be done for any system of equation, and this also gives us information about what we can do with systems:
When given two equations, it is always possible to solve for a variable in one of the systems of equations and then substitute what you found into the other.
The word system suggests something ingrained, a mechanism with different parts that work together. If all of these parts work together to help find a solution for each variable within, then it may be possible to use those individual equations to help solve for another. Sometimes, the equations need not have two different variables. Take a look at the next problem.
|
Example 2.3.c: If , what is ? It may seem unusual to use systems of equations to work these types of problems out. We believe most students will instinctively know how to work this problem out completely. Nevertheless, the relationship between the system and this problem is self-evident. There are two equations within this question; and we know to use both to solve this problem. Therefore, let the following be true:
We have two unknowns, , and we want to find , implicitly. To do that, we need to know what is. The only equation that can help us here is (). First, we need to solve for . Now that we know what equals to, we can finally find the solution set . The only equation where we can find is (). Therefore: |
At times, however, solving by substitution is not always the most efficient. For example, in this situation, it would perhaps be better to use the fact that since() has the term . The terms are similar by a constant multiple, . By this logic, implies that . By the transitive property, implies that . As such, .
Most of the time, substitution will work the fastest. However, situations may appear where elimination of a variable may improve the situation dramatically. This option has a natural reason for it working, and it all has to do with operations.
|
Example 2.3.d: If and are part of the system of equations, find and in terms of . One could take the effort of substituting each information needed to find and . However, the amount of information needed to answer this question is not enough with substitution alone. This is because of , which requires more information in order to make it way easier to manage. We will have to look at these equations together. But first, we will label them.
These two equations are part of a system. Whatever is true for one is true for the other. However, if these are part of a system, then when combining these two different relations, whatever action is done to one side must be done to the other side. This fundamental principle of algebra can be extended beyond just one system. We can sufficiently demonstrate this as such: let and . By the transitive property, or (), and or (), meaning:
If we let and stand for different equations, because those equations each have their own relation to another side by the transitive property, then combining equations is a valid action. (We learned an important fact within our problem that required demonstrating the fact to be true before we could use it. This is called a lemma, and it is often sneaky in where it shows up. Keep an eye out for lemmas.) From what we learned above, we can combine two different equations and it will not break anything. Therefore, let us find : Hopefully, by now, you can successfully follow along with the algebra without any need for guidance. Either way, we found the equation that results from adding the two relations, () and ().
If we look back at the question, we want to find in terms of , so let us do that. First simplify the equation. Notice that is a multiple on both sides of the equation, so it can safely be divided, assuming . This step will be justified in the next chapter. We are done with the first part after this: We have answered the first half of the question. However, we need to find . We can do this easily with (), since we can use the zero factor property. Let us rewrite the equation below. We may safely ignore and work with the other factor. Now solve for in terms of : We have found the two solutions to the problem: and . |
The above problem demonstrates the next principle of a system of equations, which we proved to be true in the problem above as well. The usefulness of systems of equations is the ability to combine these two principles of systems of equations to help solve problems. The conveniences of using algorithms are one of the principles by which mathematicians have lived by because it can help easily solve problems that would be nearly inconvenient or even impossible to solve without them.
When given two equations, it is always possible to combine the two equations in a system.
Systems of equations can be combined or solved individually, and these two actions can be combined in any number of ways to easily and verily solve for the two variables for which we seek. If possible, it may be best to solve by elimination, which is to combine the two equations in such a way as to eliminate one variable and solve for the other through the combined equations. This was demonstrated in the above problem, and it is how we found a useful reason for using The Second Reality of Systems.
From what you learned above, you should be able to solve any problem involving two systems of equations. Before we get back to our original problem, let us revisit a problem; however, let us add more information and change the situation a little so that we may learn how physics has found itself in this book again:
|
Example 2.3.e: Assume two blocks with non-zero masses and are attached to a pulley, where is on a wooden table with a coefficient of kinetic friction , and is suspended in the air. The following equation models the situation:
We are back again with the scary problem, only this time, with choices. The choices are a disguise of a certain problem: true-false. We want to determine which statement(s) is/are true, and only the true ones. The choices delimit our focus, and so we will focus intently on what it states. Start with the ones we can easily determine based on the information we have.
This one is the easiest to evaluate because we have all the necessary information. This is just a simple substitution exercise. If this is true, then we have found one of our answers easily. If not, then we did not waste too much time. It was pretty clear that the force of friction would not have been 9 times the mass suspended in the air because neither 10, 2, or 5 were a multiple of 9. Nevertheless, the final answer simply cemented this fate.
Look at the system of equations above. Let and . Is there any term in the equation that can be eliminated through the combination of the two equations? Yes, one can subtract from to get the following: As we now know, the following equation models the situation:
As in Example 2.2.d, we can substitute information we see familiar in the problem above. In this instance, and will be needed here. As such our next equation shows itself:
Because of the associative and commutative property of multiplication, (see Example 2.2.d in case a student needs to remember why), so the equation must be equivalent to:
Notice that is a factor of both terms on the left-hand side, so . Have the factored form rewritten below:
Recall that we are trying to solve for , so let us go ahead and divide both sides by :
At this point in time, we have all the information necessary to determine if the above statement is true. We know the following: These points above are information that can help us determine whether the acceleration is positive. This should be a good step in the right direction, because if the acceleration is negative, then we know that we are done with this problem and can move on to the other choice to evaluate if they are true. Either way, let us substitute information we know: This is the final piece of information needed to find the answer. We wanted to evaluate whether the acceleration is indeed , and sure enough we found information that stated this is a possible answer.
This is a strange statement. Based on the system of equations, if is not different for one or the other, then how is it possible for the tension to be different for each block. However, a cursory glance is not an analysis, and it is indeed certain that our conclusion is too hasty to be true. Look back at the system of equations: Now that we know what the acceleration equals, we can use that information to answer the question involving the force of tension for the block of mass (meaning we have to use the first equation to keep it in terms of ). However, in physics, it is often best to keep the solution general to make sure we learn something new with what we already know. Keeping in mind is unknown, , and . By what we know:
Here, is a factor on the right side of the equation, because We can take the opportunity to solve for found in (). Notice how Equation () shows up again on the right hand-side, only this time missing a factor of . Because , we may easily rewrite the above equation like so: Recall how , , , and . Using what we know, we may safely conclude that According to the above calculations, in terms of is nine times the mass suspended in the air. Taken literally, this is true! |
We have found useful applications of systems of equations in both real-life scenarios, abstract algebraic problems, and proofs. Nevertheless, we have still yet to learn one more tool to work with. This abstract problem below will be the last demonstration of it before we get to the two explorations.
|
Example 2.3.f: Let an initial positive number be multiplied by the mixed number with that result being divided by the sum of the initial number and . Then, subtract the result of that by the ratio of another number to the original. This operation results in . Given twice the reciprocal of twice the sum between the initial number and the mixed number minus the result of that to half the other number will equal times half the original number, find the greater. This type of question is hard enough to answer for the average student since most students have experience with answering questions that are usually straightforward with some context. However, this question is something one would see if one were in a math competition (despite the confusing language). Here is a nice tip to keep in mind. Anytime the problem seems to be wordy, make it into an equation! This makes problems so much easier, as you hopefully figured out by now. Let us go ahead and decode this problem. Let the initial number be and the other number be . Let us go ahead figure out what the problem says. Note: a mixed fraction of is the same as , so we will be using this from here on.
In simple terms, is multiplied by . Afterwards, that product is then divided by the sum of those two numbers. Therefore, the expression is
Subtract the previous expression with , leaving you with a continuation:
Make this expression equal to , thereby giving you the first of many equations in this problem.
That is a little too much, so let us further chunk that information.
Despite these scary-looking equations, we have made our lives much easier. Now we simply have to find one of the numbers, whether the initial or the other. In this instance, it would be much easier to find the initial number because we can find a way to eliminate the other. Recall how we simply just allowed the two equations to be added upon the other. We justified this through the transitive property. Plus, we introduced equations through the principle that whatever is done to one side must be done to the other due to the property of equality. Well, since adding and multiplying are definite candidates, then one can say that multiplying the entire equation would work out in our favor. Therefore, multiplying the two equations by any factor is okay. Because this principle works in isolation, we need to make sure it works when combined with what we already know. Let the following be true:
Our goal here is to transform to , so that we may do a version of the following operation: . This will eliminate , highlighted in red in (). First, notice there is a common factor of in . Since does not have a factor of , we may multiply by to have a common factor of between and . The operation below will color the thing of interest we are trying to eliminate in red (to the best of our abilities). This gives us the following: This same principle is applied to the right-hand side of Equation (), and since the exercise for that is trivial, we will leave all the calculations in between the final answer to the reader as an exercise. From here, this gives us out next equation.
The highlighted variable of interest in red has a factor of that is not found in the goal, , so one will need to divide by so that it cancels out and gets us closer to . (Alternatively, one could multiply by because of a basic principle of multiplication — a negative times a negative equals a positive.) We will leave this critical operation as an exercise for the reader since the difficulty of this step is trivial. One factor missing as a result of this manipulation is since the only difference between and is the factor of . As such, this needs to be multiplied onto . As such, the following operation is true: Our plan has finally been revealed — the goal is accomplished. Let . By what we have proven in Example 2.3.d, the lemma shows that we can combine to equations through addition or subtraction. However, based on what was stated, when doing the operation , by the transitive property, , meaning we can combine two equations when multiplying by either a constant or variable. This is our lemma! The operation is true. First, we will write the result of our work through the problem. (Also, the other side of the equation is also left as another trivial exercise for the reader.)
All that is left to do is do the operation we have been waiting for:
This is all but the first phase of our plan. Now we need to solve for . It would be nice to evaluate the expression with a common denominator because we can make use of the zero factor theorem. After all, the denominator cannot be set equal to zero, yet the fractional term is zero. Therefore, the numerator must be zero. It would be easy to evaluate if the fraction was singular. Notice how the denominator term has a common factor of (in red). Because of the way the problem was designed, the missing factor is . As such, it would be best to multiply to the first fraction. If you don't understand, it may be best to follow along below:
Because the fractional term is equal to zero, this must mean the numerator must equal zero. Therefore, we will only look at the numerator to make our life easier:
The following factorized form may appear to come out of nowhere. However, this will be explained in the Polynomials chapter of this Wikibooks. For now, simply pretend you understand and follow along:
The problem states we started with an initial positive number. Therefore, we will only look at the equation that will give a positive solution to this equation. Before declare we are done with the problem, let us make sure we are being mathematically valid. We need to make sure we are not falling into the trap of making () a situation. To do that, we may use the zero factor theorem to our advantage. Because we must not allow the denominator to equal , if we set the denominator to zero, we know what cannot equal. If our solution turns out to make the denominator equal to zero, then we have no solution to the original problem of the question asked.
Per the zero factor theorem, and . "Solving" for tells us that our solution does not make the denominator equal to zero. Although we will not explicitly prove it, it is obvious that is a valid solution. Some of our readers might think the problem is over. However, we are barely in phase two of our plan to find the solution. The problem has asked us to find the greater or the number that is the greatest and to declare the magnitude of that number. As such, we need to solve for and compare it to before we say we are finished with the problem. This may waste time if we found the greater number, but it will make us lose points if we find the wrong number, so it is better to determine the answer. Since () and () have some , we will use one of those two equations. If a person is clever, one might try to work with one of the simplified equations. We will allow that student to be clever. We will choose to go with () since we will not have to substitute for a lot, which will make calculations easier as a result. No matter what equation the student chooses (that has a ), the calculations will be ugly.
Let us hope the marking scheme we have devised below is easy to follow. Any numbers that can be eliminated will be highlighted in Red while terms that can be factored will be in Green. Also, if you recall, the square root function has some strange property whereby multiplying the number to itself will result in the number inside the square root (such operations are colored in Orange). With this information in mind, let us apply some math:
We are nearly finished with our plan. We simply need to solve for . The easy way to do it is by multiplying both sides by the denominator of the left side of Equation (). From there, it is easy to show that without needing to complete the calculation fully. We will leave that step as a non-trivial exercise for the reader. With the information we have provided, it is safe to say that and so the greater is . In terms of magnitude, the greater is |
This example was used to introduce the important proof of concept, so to speak, involving the manipulations allowed over a system of equations. If one knows about the induction hypothesis, one can easily prove the manipulations we have formulated regarding the system of equations applies for any system involving equations. Either way, our final reality of systems reveals itself:
When given two equations, it is always possible to combine the two equations in a system such that at least one equation in that system was multiplied by a constant.
The three realities described herein will work for any problem involving systems of equations in some way. We will explore these ideas more in the second set of chapters in this Wikibooks, including the idea of more than two equations. For now, let us explore this concept to its fullest.
Note: required for the next exploration is the difference of squares formula: . An explanation for the formula can be found in our Polynomials chapter.
Since there are two equations that have the same variables, put them into a systems of equations: The following statement is also true due to cross multiplying: From there, solve:
Substitute the value into the system of equation for the second equation and solve for :
After wards, put the two derived equations into another systems of equation and solve down for and : Add the two equations and solve for :
- .
Substitute into either equation and solve for : .
Because , .More explorations will be added later.
Solving for Variables in Inequalities
editThere are many times where we need to know about what values for some variables could tell us about the restriction of the overall operation. For example, we may need to know about the restriction of the variable so that we may be allowed to meet some certain criteria.
An inequality is an equality where one side may not precisely equal the other. That is to say that the one side may be greater than () or less than () the other. From these, truths can extend. This possibility gives us our first property.
For any two real numbers and , there exists only one of these possibilities:
This property states that no two numbers can ever be less than and equal to. This is impossible. This is what is referred to as a strict inequality.
There exists a greater than or equal to () and a less than or equal to (). However, for a greater than or equal to, it is simply saying that , where either is greater than or . It is not saying it is both, but a possibility of both exists. The same reasoning applies for a less than or equal to. As such, a number can only ever be in one of the states above.
For any three real numbers , , and , there exists only one of these possibilities:
- If , then .
- If , then .
For when either premise is a strict inequality, then the conclusion is a strict inequality:
- If , then .
- If , then .
- If , then .
- If , then .
This property should make sense. Suppose . Because and , we can safely conclude . This property is very important when it comes to finding inequalities that are similar, and especially when wanting to show that some inequality may be impossible. Notice how is equivalent to "and ." This is called chained notation.
For any two real numbers and , we can conclude that:
- If , then .
- If , then .
This should make sense. If , then obviously . Because this is a property, it is defined true.
For any three real numbers , , and , adding any real number to both sides of an inequality give the following result:
- For , .
- For , .
Let us say that a number exists in the state whereby . If adding another real number to both sides of the inequality, then . This makes sense because if , then adding another constant to the both sides will not in any effect change the inequality because both grew by the same amount. As such, is still less than .
There is similar idea to this for multiplying the two sides by the same real number. However, it is a little more complex than that. We need to look at the cases for and . Let there be two real numbers and such that . If multiplying by to both sides, then because both sides are multiplied by the same number, so the product must still be .
For any three real numbers , , and , multiplying real number to both sides of an inequality give the following result:
- If and , then .
- If and , then .
- If and , then .
- If and , then .
A similar idea for division exists for any
For any three real numbers , , and , dividing by the real number to both sides of an inequality give the following result:
- If and , then .
- If and , then .
- If and , then .
- If and , then .
These properties have their special cases that are very useful in some problems, especially with systems of inequalities.
For any two real numbers and , multiplying both sides by to both sides of an inequality give the following result:
- If , then .
- If , then .
- If , then .
- If , then .
For any two real non-zero numbers and , making both sides its additive inverse makes it so that:
- If , then .
- If , then .
- If , then .
- If , then .
While these properties are much more plentiful than the properties of equalities, it is important to understand these properties, especially when working with systems of equations.
More will be added later.
Exercises
editDirections: Some questions will require you to select from among five choices. For these questions, select the BEST of the choices given.
Some questions will require you to type a numerical answer in the box provided.
Some questions will require you to select one or more answer choices.
More will be added later.
Summary
editFootnotes
edit- The "force" on the car would be referring to the net force, which is . The acceleration , which is given in the problem as . The mass . From here, we would determine the net force to be .
- Notice how we mentioned that or . This is the case because it is not always the true that both must equal zero. We only need at least one to be true. Here, , which is not zero! However, in the context of the algebra, we are saying that if we were to have the factored form with , then we may state that the factor or the factor , so that we may ignore to find out more about . After learning about this, we now know for sure that . Otherwise, the equation makes no sense. Alternatively, if one did not see the factor of in both terms, then one could have simply done the same procedure but then multiplied by . Here is precisely what we mean:
Exercises and Practice Test
edit
Intro to Algebraic Proofs
To certain students, math feels like a memorized set of rules. However, the only things that students may ever need to memorize in algebra are the basics of what is true about the object being studied and some notation. Any and all properties that students may feel like they need to remember are actually something someone can derive from the foundations they actually should remember.
In this page, we will introduce laws of logic and properties of conditional statements. We will be applying the laws of real numbers and algebra to prove some often-used theorems. Finally, we will use algebra to demonstrate a mathematical statement as true.
Introduction to Sets
editThe basic understanding of anything related to mathematics begins with learning about sets. While this will not be a substitute to a discrete math class (or the CLEP College Mathematics exam), some concepts you usually learn in there will be introduced much earlier on. As such, we will attempt to make this introduction intuitive and easy-to-understand. Finally, learning about sets and logic can easily help you in real world situations (moreso logic), especially in the context of probability.
Most people will imagine a set as an aggregation of objects (called elements) that which is defined. However, there needs to be a restriction.
A set is a "well-defined" collection of objects, known as elements. A set is usually denoted by a singular, capital letter.
Here is a question: can a set contain itself? If there is such a thing as the set that contains all sets, then the set that does not contain itself would be in the set. However, that is impossible; that set would not be in itself but can not be defined as such because this set contains all sets. Since it is impossible to define whether it is a set under this such definition, the set that contains all sets cannot be possible (this paradox is known as Russel's Paradox). The restriction that a set must be well-defined is a necessity for this reason.
"Well-defined" is vague for now, but the restrictions for what constitutes "well-defined" is beyond the scope of this text. For those that are curious, understanding Zermelo–Fraenkel set theory would be important (although a little high level for what we want to accomplish in College Algebra).
A set can contain any number of objects. For example, we could have a set that contains all of the positive, even, single-place numbers, . We could also have a set that contains nothing (we call that the empty-set, ). We could also have the set of common breakfast drinks, .
Note how we define the set. The way we define it is with curly braces, with the elements denoted and separated by commas. Sets are also unordered, meaning that the order of the elements in the set does not change whether one set is equal to another. Thus, if is defined as earlier, and , then . This tells us something very important about sets.
The Elements Define a Set
editBy what we defined, a set is a collection of elements. This means the objects define the set. Remember, this is true by definition, so this is sound logic.
Let there be a set containing (or not containing) an object . The object is in is written as . Otherwise, if is not in , then .
If there are two sets, and , then one of the sets can contain the other as an element, such as . If otherwise, then . Consequently, the question of whether or not a set is contained within another is a question of conditional logic: it is "true" that or it is "not true" that . There is no in-between option.
A set can only ever equal another if they contain the same elements. The order of the elements do not matter, so long as the element of each corresponds through its definition, and the number of the elements within each set is also identical. This therefore means a set is uniquely determined by its elements.
|
Example 1.1.(a): Set Conundrum Let and .
Answers: (a) . (b) but AND but . Explanation for (a) and (b): These are mostly self-explanatory. Keep in mind that any set within another set is defined as the element of the set. However, if that element contains any objects, then it is not part of the "parent" set. For example, let . Here . We know and . However, any element in does not define . The elements only define its own set. |
How to define a set contains an element is done in two different ways, explicitly and implicitly.
Let there be a set such that . The explicit definition of a set is written using curly brackets, known as set braces— — as below:
- , whereby all and only the elements found in must be written within the set braces.
The way the above set is read is is the set that contains .
The explicit way of defining a set is what we have been using throughout the entire section. However, this can also tend to be very useless when there are an infinite number of elements in the set. The next definition should held us in that aspect.
Let there be a set such that . The implicit definition of a set is written using set braces and ellipses given a pattern is demonstrated with the elements of the set, as below:
- .
The way the above set is read as follows: is the set that contains , and so on, up to .
A more robust definition of a set is thus the following:
A set, usually denoted by a singular letter, is a "well-defined" collection of objects, known as elements. A set is also uniquely defined by its elements.
Because elements define the set, it is often important to know the size of the set. This is known as the cardinality or size of the set. Because we want to keep this part of the subject intuitive, we will use size from here on.
A set with elements has a size of , denoted as
|
Example 1.1.(b): Breakfast set Let be the set of common breakfast drinks. A non-comprehensive list of the most common breakfast drinks in the U.S. are given: Coffee, Milk, Orange Juice, Apple Juice, Water.
Answers: (a) . (b) . Explanation for (a) and (b): These are mostly self-explanatory. The number of the items in the list is five, so the size of the set is five. |
Check your Understanding
editDirections: Some questions will require you to select from among five choices. For these questions, select the BEST of the choices given.
Some questions will require you to type a numerical answer in the box provided.
Some questions will require you to select one or more answer choices.
More questions added later.
Properties Define an Element, Ergo, the Set
editAn object can have properties that would be important to write down. If the object itself changes because of it, then it is important to have that defined. These are referred to as conditionals (the more common one is propositional functions, but this is avoided in the interest of providing a definition of functions that is not treated as tautological when the definition of a function is non-tautological).
Let there be an operation such that the object variables give a truth value depending on either the values of the variables or the operation of (its "nature"). This is a conditional.
Since a set is defined by its objects, the conditional also defines the set. The notation for a given set that has a conditional is
- or
where such a set is read as is the set of all such that is true. The term "such as" originates from either the vertical bar ( ) or the colon ( ). In this textbook, we will use the vertical bar to refer to "such as" since this is standard in most College Algebra courses.
A special type of notation is used when a set can better represented through conditionals. Take the set of all Fibonacci numbers, for example, :
- .
This set can be listed implicitly. However, when there is a pattern to the set's elements, then a set can become much more useful. Let represent the index of the Fibonacci sequence, where is an index starting at zero. The set can be equivalently written as the following:
- .
While this notation seems to hurt rather than help (and seem more confusing), in actuality, this tells us a lot of information about the set, including the pattern used, what initial conditions are necessary for the set to exist, and what set need to belong to for this pattern to work.
A special case of set notation in which a set of elements can be more usefully listed with or too large to list with normal set notation.
We read the notation, " is the set of all such that is true." Here, is an expression and is a rule or condition.
We can now easily read sets. Looking back at the set (the set of Fibonacci numbers):
.
is the set of all such that , belong to the set of positive numbers, and there are two initial conditions, .
|
Example 1.2.(a): Set-builder notation Write each of the following using set-builder notation and implicit or explicit notation.
Answers: (a) . (b) . (c) . (d) . (e) . (f) . Explanations:
These are mostly self-explanatory. Note that there are two possible answers we could write. and are both expressions. However, to make sure both are equivalent, we need a rule so that the expressions can the elements in the set are equal to the other. Similar for (b).
The pair of solutions is given by the expression of some or . The rule is the equation itself since it describes how one finds the solution set. This is all that is needed for the set-builder notation. To obtain the solutions in the set, simply solve: By the zero factor theorem, This is where the explicit set notation comes. Because the natural numbers do not have negative numbers, fractions, or square roots, the natural number set of solutions is only . This type of analysis allows us to determine that one of the sets, see item (f), is empty, and is therefore equivalent to the empty set, . |
Check your Understanding
editDirections: Some questions will require you to select from among five choices. For these questions, select the BEST of the choices given.
Some questions will require you to type a numerical answer in the box provided.
Some questions will require you to select one or more answer choices.
More questions added later.
Comparing Sets
editOf course, many sets are similar to another. As such, many mathematicians find it very helpful to compare sets. Some vocabulary terms will be listed here.
Suppose and are sets. If each element is also in , then is a subset of . This is written as
If there is at least one element such that , then is not a subset of , or
- .
The idea of the subset is very simple; however, it can be very powerful when comparing two sets. Nevertheless, many students may neglect to take care in their notation while trying to compare sets. The examples presented below are correctly stated. The reasoning is given as well. This type of reasoning will be required for you to identify subsets and non-subsets.
- .
- Because , (the set) is a subset of .
- .
- Because , is a subset of .
- .
- Although , the elements of set cannot be found in the set . In other words, .
- .
- Because , . If one cannot see this, let . Notice that . Because , .
One other definition that is useful to know is the superset. The definition is complex yet the intuition is rather simple.
Suppose and are sets. is the superset of if , which is denoted as
If , then is not a superset of , or
- .
Some examples below will be listed below, along with an explanation. Notice they are the same as above.
- .
- Because , .
- .
- Because , .
- .
- Because , .
- .
- Because , .
- .
- Because , .
Check your Understanding
editDirections: For each of the following conditions stated below, four to five lines will be provided. Identify the correct definition that would apply to the given set for the one provided in the problem. Some problems require multiple correct answers and as such multiple selections.
Combining Sets
editThe process of combining sets can be very useful, especially when working in contexts of probability.
Suppose and are sets. The union of sets and is the set .
If you want to explain this a five-year-old: the "union set" is the set that contains all things in and .
A few examples are presented below, where , , and . These are all the possible combinations of the sets (excluding combinations with its own set).
Suppose and are sets. The intersection of sets and is the set .
If you want to explain this a five-year-old: the "intersection set" is the set that contains all things that are found in both and .
A few examples are presented below, where , , and . These are all the possible combinations of the sets (excluding combinations with its own set).
Suppose and are sets. The difference of sets and is the set .
If you want to explain this a five-year-old: the "difference set" is the set that contains elements of but excluding what are also found in or are in .
Several examples are presented below, where , , and . These are all the possible combinations of the sets (excluding combinations with its own set and any combinations with all three sets).
Check your Understanding
editIntroduction to Logic
editLogic is important in many fields. However, it is especially in mathematics since without this tool, we could not be able to come up with theorems nor algorithms. That is why it is especially important for us to teach this tool. While this may not be a philosophy class, we will be teaching as much as needed for us to be able to present proofs to you without too much trouble.
Logic is the process of deducing information correctly, not necessarily obtaining the correct information.
The process of deduction is simply the ability to "connect" statements through some related way.
For example, we know that Aristotle is a "grefunkle," and "grefunkles" are "prostireoni." Therefore, Aristotle is a "prostireonis."
Now, "grefunkles" and "prostireoni" are made up words; these things do not exist. However, the sentence we made is logically correct. Remember, logic does not require the correct information, so this sentence is logically correct while not essentially correct.
Statements
editLogic must begin with "statements." After all, the example we presented could not exist without "statements."
A Statement is a sentence or mathematical expression or equation that is either true or false with no in-between.
The truth value is the proposition of a statement's truth. These truth values are almost always "true" or "false," especially in classical logic.
Statements need a "verb" of some kind, mostly "declaratory verbs," like "is" or "are." For example, "Apples are blue" is a statement since it is either true or false (here, it is false for many apples). Questions are not statements. More examples are provided.
- Every even number is divisible by itself and two. True.
- All prime numbers are odd. False.
- Twelve more than twenty-two less than the initial means that the initial is twenty-two more than twelve less than the result. True.
- If a side of a parallelogram is , then the area of the parallelogram is . False.
- The side length of any one side of an isosceles triangle is equal to the square root of the two remaining sides. False.
- If one and only one side of a quadrilateral is not parallel to its opposing side, then it is a trapezoid. True.
Statements #4 and #6 are a type of statement we will be discussing very closely in this section. Keep in mind the form of the sentence for future reference.
Notice how statement #4 contains a variable . A statement may use variables so long as no matter what the variable stands for or what the variable will equal to, the statement will always either be true or false by simply the statement alone. We will discuss this more in this section.
Also the statements do not have to be sentences, as has been stated in the definition:
- True
- False.
- True
- False.
- True
- True
Keep in mind that the mathematical expressions you use need to state something in the "declaratory verb" form we describe. For example, states in a more compact form is an element of the set of natural numbers, so this is a valid statement. What would not be a valid statement is simply (the set of natural numbers). This tells us nothing.
Statements can be used many times in a proof or even a math problem. This is why mathematicians have developed tools to be able to declare statements using only one letter, usually . Subscripts are used when more than four statements are necessary, although one may be allowed to use more than the letters provided (if somewhat unconventional).
- There are more than two different letters in the word "cranberry." True.
- The sum of the digits of any three digit number is between and . True.
- Any two consecutive primes have a distance of six between them. False.
- . True.
With , the parenthetical statement tells us that there are two variables within a statement. This is a notation because at times, the variables become very important to determine its truth value. This will be explained shortly.
As another rule of thumb, if a sentence does not describe anything about a subject, then it is not a statement. Here are a few examples of non-statements.
- The set and .
- What is ?
- .
The final bullet point is a tricky one for students unfamiliar with identifying statements. Some will say this is a statement because it is either true or false that is equal to . However, if you think about it, this statement is entirely dependent on the value of . This is called an open sentence.
An open sentence is a sentence or mathematical expression or equation that depends on the value of its variables.
Look back at the open sentence. Let . If , then is true. Otherwise, it is false. This is why is not a statement. It depends on the value of . A statement needs to be either true or false but not due to a changing artifact.
One important topic to discuss when working with statements is the negation.
Given a statement , the negation of statement makes the truth value of opposite its original value.
When we take a statement and we negate it, we make a true statement false or a false statement true. Take the following as a couple or examples:
- Every even number is not divisible by itself and two. False.
- Some prime numbers are not odd. True.
The second example required us to make the "all" into "some." More information about how and when this is done will be shown later.
The examples above are from the beginning. Notice how we made these statements opposite their truth value from the beginning. Mathematicians use these so often that we have a notation for it.
Given a statement , the truth value of (or ) (which both can be read as "not " or "it is not the case that ") depends on the truth value of only , where this negation symbol means "not" or "it is not the case that." This textbook will prefer the symbol but is used more often in proof classes.
Suppose . For to have a truth value of (true), it is required for to be false. Otherwise, is (false). This can be further shown using this simple truth table (a table that shows the truth values of each individual statement and the resulting column):
Properties of Conditional and Biconditional Statements
editConditional Statements
editIf you want to have any hope of understanding mathematical theorems at a deeper level, then you will need to understand conditional statements.
A sentence written in the form of "If P then Q" (usually), where is under the condition of 's truth value, is a conditional statement. A conditional statement is only false when is true but leads to a false .
Other ways in which this sentence can be written is presented below:
- " if "
- " only if "
- "Whenever , then also "
- " is a sufficient condition of "
- " is a necessary condition for "
Here are some examples:
- If you pass this final exam, you pass the course.
- You can travel to Spain if you learn the Spanish language and culture.
- Garfunkles are prostireoni only if at least 100 years have passed between garfunkles and prostireoni.
- Whenever you lose power, then you also lose heat.
- Composing good music is a sufficient condition of getting paid $100,000.
- Getting famous is a necessary condition for writing the best calculus textbook.
Conditional statements have a sufficient condition (after the "if") – or a hypothesis – and a necessary condition (after the "then") – or a conclusion. This is why if our true hypothesis leads to a false conclusion (the result is different from our stated conclusion), then the conditional statement is false.
Mathematics is a big friend of the conditional statement. Here are some familiar statements using the conditional statement.
- If a right triangle has leg lengths and hypotenuse , then .
- if is a finite set.
- are one-to-one only if for some real numbers .
Because these type of statements are so important, it is necessary to understand how they work. There is a short-hand notation for these statements, which is presented below.
Given two statements and , the truth value of (read as "if then " or " implies ") depends on the truth values of and , where this "right arrow" symbol means "implies."
The way we determine the truth value for is to write a truth table. We can determine each row of the truth table by simply looking back at the definition of conditional statements.
A conditional statement is true if the sufficient condition leads to the stated conclusion. That is why the second row gives us the result of a false truth value. This still explains the two final statements: if we have a false hypothesis but the conclusion is true, then either way, something true did happen but not as a result of the hypothesis. The hypothesis is not necessarily required for a conditional statement to be true so long as the conclusion is true. Finally, whenever a false hypothesis leads to a false conclusion, then that makes the conditional statement true because something false leading to something false is itself a confirmation of the conditional statement.
|
Example 2.2(a): A stern rule follower. There are six rules to be able to enter or stay in a non-specific kid's music club. If at least one of these rules does not apply to the student, they will be placed in the teen's music club (covered by rule #5) or will be given a one month grace period if not over twelve years of age. The one month grace period will not be invoked if one is in the kid's or teen's music club.
Items (a)-(d) below have a few situations. Determine if there is enough information to kick these people out (whether temporarily or permanently) of the club based on their descriptions. Provide a reason for each of the young people below. Otherwise, state that individual as allowed to stay.
Items (e)-(f) ask you a couple of questions regarding the situation provided. Answer items (e)-(f).
Answers:
Explanation More will be added later. |
Biconditional Statements
editConditional statements also have its different, non-equivalent forms. These statements are not equivalent because their truth values can be different. Notice how the end result is different simply by switching the conclusion and the hypothesis.
By this brute force method, we were able to show that these statements are not equivalent. These statements are equivalent if both and are true. However these two statements can be true depending on the statements. Real life examples are rare.
Here is a conditional statement that has a true converse: "If a phrase is chromatic, then it contains notes separated by half-steps." The converse of the statement is "If a phrase contains notes separated by half-steps, then the phrase is chromatic." The reason why is because a chromatic phrase, by definition, uses notes separated by half-step, so both (the conditional statement) and (the converse) are true.
In situations where both the conditional and converse is true, you obtain a biconditional statement.
A biconditional statement is a sentence or mathematical expression or equation in which the conditional statement and the converse are true for any combination of .
Biconditional statements require that the conditional statement is true. Therefore, only if . However, the converse is also true, so if . As such, we say a statement is biconditional by stating that " if and only if ."
A biconditional statement can be written with the following notation: (read aloud as " if and only if " or " is equivalent to ").
Because it requires that and be true, it will mean that the middle rows will be false. Thus, the following truth table results:
More detail will be provided as to why this is true by looking at the next section.
More will be provided later.
Related Forms of Conditional Statements
editThe related forms of conditional statements are of great importance. However, some proofs classes ignore the different forms of the conditionals statements. However, at times, proving a conditional statement involve proving all of the three related forms.
A converse statement is a sentence or mathematical expression or equation formed by exchanging the hypothesis for the conclusion and vice-versa. It is of the form for conclusion and hypothesis in the original conditional statement.
An inverse statement is a sentence or mathematical expression or equation formed by negating the hypothesis and conclusion. It is of the form for conclusion and hypothesis in the original conditional statement.
An inverse statement is a sentence or mathematical expression or equation formed by negating the hypothesis and conclusion and exchanging their negated statements for the other. It is of the form for conclusion and hypothesis in the original conditional statement.
A mathematician's job is to test the limits of their statements and find what can be true or false.
There are some properties of the related statements that are not often taught. However, we feel it may be at least somewhat important to understand that these statements exist and that there may be some logical equivalences.
If a conditional statement, , is true, then the contrapositive, is true.
A good way to see this property is true is with a truth table:
Hopefully, it is clear why these are related statements. Because the negation of and the negation of , and the order of the hypothesis and conclusion require that the truth values consequently change. Thus, these statements are logically equivalent.
The same can be shown with the inverse and the converse.
If a converse statement, , is true, then the inverse, is true.
More will be added later.
Combining Statements
editThere are many times in life we have to think about the truth of a statement which contains two statements. For example, "The light is on and the light is off." This statement is definitely false. How do we know? Because of the word and.
Let : "The light is on and the light is off." Notice how we can break the one large statement into two small statements thanks to the conjunction and. As such, let : "The light is on" and : "The light is off." According to the English language, "on" is opposite in meaning to "off." However, a lightbulb can only even be on or off. Thus, if is true, then is false by default. Therefore, is false.
The process of combining statements will be very useful in proofs. Since these combinations are defined by themselves, we do not need to prove them. Finally, because this combination is based entirely on the english language, the truth of a statement can be easily determined.
Based on what we did with the introductory example, let us generalize what we did.
Given two statements and , the truth value of (read as and ) depends on both and , where this "wedge" symbol means "and."
Suppose . For to have a truth value of (true), it is required for both to be true and to be true. If either one is false, or both is false, then is (false). This can be further shown using a truth table.
Given two statements and , the truth value of (read as or ) depends on the truth value of at least one, or , where this "vee" symbol means "or."
Suppose . For to have a truth value of (false), it is required for both to be false and to be false. If either one is true, or both is true, then is (true). This can be further shown using a truth table:
By using these conjunctions and truth tables, we can easily determine when a open sentence will be true and whether a statement will be true or false.
|
Example 2.3(a): Finding truth in sentences and statements. Read the open sentence below that someone claims to always be false for any .
Answer items (a)-(c) below.
Answers:
Explanation (a): Because is negative, . Because is positive, . Finally, because , it means that it is not the case that , so . Knowing that these statements are in tandem with each other according to the English language, all statements are combined with an and. All a "but" means is an "and," with emphasis. (b): Explanation already given in Answers. (c): Because there are three variables, and each of either a or truth value, there are possible truth values for the final open sentence. The most organized way to check how many possible open sentences are false is through the truth table. |
More will be added later.
Logical Equivalences
editMore will be added later.
Symbolic Logic
editMore will be added later.
Quantifiers
editMore will be added later.
Proving Mathematical Properties
editApplying Laws of Real Numbers to Verify and Prove Mathematical Properties
edit|
Example 3.1(a): Verify where . Verification is an easy task since all you have to do is rewrite the equation we see above and change only one side. Because only one side changes, a chain of transitive properties may be applied to that side, until one reaches the final conclusion: a simple statement as a property of equality to itself. This may be easier to show than explain, so simply follow along with us.
According to the definition of division, . Since this is true per each division found in the right expression, () can be rewritten as the following:
Notice how each term in the right-hand side of the equation has a factor of therein. Because that is true, the following is true of the right-hand side of the equation.
By the definition of division, the right-hand side of the equation is equivalent to , so
Notice how the chain of equations herein can connect to every equality. Since () and () is true, we know the following equation below is true:
Because () and () is true, we know this below equation is true, and so on:
As shown in (), we have verified the truth, and are therefore done with the problem. The "chain of equations" below shall perhaps show this chain of "change of one side only." |
It is important to take note the language of the directive verbs found within the prompt in the example above. By asking the examinee to verify, it, in effect, tests the understanding of the writer to communicate how a certain statement can be made true by only validly changing one side.
In the example above, we decided to change the right-hand side of Equation (). Here is a question for the reader: "Why did we decide to change that side only?" If you can answer this question with precision before the next two examples, then it is safe to infer that this student understands how to verify literal equations.
Note: despite being an important skill, it would be impossible to show this type of understanding on a multiple choice exam. Nevertheless, the journey of the mathematician is of the skeptic of statements made. You cannot fully regard a statement as true if you do not know the proof of it or the verification of it.
|
Example 3.1(b): Verify in . This equation is not literal, so it is not necessary to change only one side to become the other. Nevertheless, it is not necessary one needs to solve the single-variable equation either. Instead, it may be easiest to simply substitute into the above equation. We shall do exactly that. Because both sides of the equation are equal, we have verified is true. |
One more example will be added later.
|
Example 3.1(d): Prove , where , , , and . This problem is a little different from the previous ones because the examinee needs to show something is true by what they are given, as well as demonstrate something is true through the derivation of different formulae and equations from fundamental properties. The importance of mathematical communication is what is tested here. The mathematician needs to describe what is given, or else, the proof will not follow logically as a form of deductive reasoning. We cannot follow the strategy we had for the previous two problems. This is because we are trying to communicate that a statement is beyond a shadow of a doubt true! With verification, we could assume the final statement is true, and thereby work backwards from where we started. However, when proving something, we have to show that when only given one statement, we can fully derive the other side without going backwards from where we started. Understanding this distinction is crucial! Let us first start with rewriting the expression into its equivalent:
Notice how we can apply a property of multiplication, that multiplying real numbers (and by extension integers) is associative. Therefore, we may rewrite () as the following:
() has the term . We can apply a property (proven in the exponents chapter) that . As such, we learn
With this, we are done with the proof. |
There is a very subtle distinction here between a proof and a verification. If we were asked to verify the statement above, we would assume what we are given here is true and simply only change one side. However, notice how we started the proof in Example 3.1.d: "Let us first start with rewriting the expression..."
In a proof, starting with the conclusion is absolutely wrong and should not be allowed because such an argument is circular! Whenever working with deductive proofs, we start with what is given and try to derive a true statement from what we started. This is one of the fundamental properties of deductive proofs.
Usually, in proofs, especially in deductive ones, there are two principles in mind that are necessary in the development of further understanding: A "universal proposition," such as a theorem or definition, will imply a "singular proposition," such as a premise, conclusion, or intermediate conclusion. Either that or a singular proposition implies another singular proposition.
For this proof, the former is true (a universal proposition implied a singular proposition). By such an action, we can verify the validity of this proof. Although one may not call this a formal proof, per se, such proof did indeed follow from verified axioms, and since those axioms are true, and it led to a truth statement, this proof is valid.
As a student further explores mathematics, principles of proof and the formality of such proofs will be very important in the life of the mathematician. In exploration of such concepts, a deeper understanding will be essential, where further examination of logic will be in order, and different types of proofs will be categorized, explained, and used, sometimes with little delay in thought.
While this is not meant to be a further exploration nor explanation of proofs in general, this book does seek to further a student's foundation of such concepts before one gets into a discrete math class.
|
Example 3.1(e): Prove , where , , , and . Let us first start with what we are given: . One common trick done in proofs is to find a way to change the expression to make things easier on us without changing the meaning of the expression itself. For example, if one wanted to find the solution to , one may want to isolate the variable . However, that cannot be done if the five is in the way, so one could subtract the five. This would change the meaning of the equation unless it is also done to the other side. This same principle could apply to proofs. Here are some common ways in which a mathematician could make their lives easier. Let be an expression of interest:
The last bullet point shall be the trick we employ for this proof. After all, we are working with fractions. However, this constant cannot simply be any number. We shall be clever and select a number that will eliminate certain terms within. This will make our life easier in the long run. First, we begin by stating the Equality Postulate (an item must equal itself):
From there, we multiply to the right side. After all, this will simplify to (), so nothing changes.
Next, apply the distributive property to the right hand side of ().
Here is the special part of the proof. Notice how that there are two terms in which two fractions are multiplied against another. We can use the property we proved in Example 3.1.d.
As before, we colored all terms that are red as terms that can be canceled. We will leave this as a trivial exercise for the reader to prove this is true. This gives us our subsequent equation:
We can rewrite the rightmost side of () as . The factorable term is in blue. Therefore, we know the following can be rewritten as the final equation.
The entire argument above can be condensed into the following compact argument: |
Applying Laws of Real Numbers to Derive New Mathematical Properties
editProofs are not only useful when it comes to algebraic statements but also mathematical properties in general. It may be the case that these such items are much more useful towards the latter than the former because the laws of real numbers are by themselves always true. Although empirical evidence satisfy scientists, mathematicians differ in that regard.
If at some point, we found a location in which an mathematical "property" were to be false, then we would need to modify that statement. From thereon, we need to do the same to other items that also use this property, which may include absolute statements, such as theorems. If a specific location fails and that specific location is integral to the proof, then the proof of that theorem is automatically invalid. We do not wish for this "domino effect" to occur, so we must prove statements are true through deduction (or induction, which we will not discuss).
Let us take a look at division properties again.
|
Example 3.2(a): Examine the two below properties listed below when dividing. Try to find a possible error in the proofs.
In both proofs (a) and (b), it relied on the property that . While there is a zero factor theorem, this does not necessarily mean that the products of two numbers, one being zero, equals zero. Therefore, this proof may be false. One needs to prove that any number times zero equals zero. |
This may seem a little nit-picky. However, this can be very important when it comes to mathematical properties. If we assumed this were true, we may fundamentally be wrong about some solutions to rational equations, may fundamentally break some models of the universe, and may fundamentally conclude absurd ideas due to a wrong assumption. Therefore, mathematicians need to be picky!
Let us therefore start this section with a proof of this statement: any number times zero is equal to zero.
|
Example 3.2(b): Prove any real number multiplied by zero gives zero. Let be multiplied by zero. Subtract to both sides of equation. Suppose Already shown that . Ergo, By transitive property, Factor : By the property, |
In the mean time, the property we used for this proof will not be proven until the Exponents chapter. For now, this proof should be sufficient grounds to accept the properties of rational numbers as shown in Example 3.2.a.
The next property we will prove has usually been proven in Geometry classes due to its simplicity. However, will do these two proofs next because we want to show a semi-formal proof.
|
Example 3.2(c): Does adding an even number to another even number equal an even number? Let , , and . If , then is even. If , then is odd. Let and . Let . From this, if are even, then is even. |
|
Example 3.2(d): Prove any two odd numbers give an even number. This proof will be finished later. |
More will be added later.
Exponents
Imagine there was a natural number that was added to itself repeatedly over times. The integer is called the multiplicand (the thing being multiplied) while is the multiplier (the thing you are multiplying to the multiplicand). The result of this operation is the product. We refer to this specialized operation, , as multiplication, which is one of the definitions of multiplication:
This idea does not seem to work for integers. Let and be a part of, henceforth referred to, multiplication function . If , then how can a number be added to itself negative times?
This dilemma requires us to work through a special case of and . Let us say the following is true: and whereby and . Let us go ahead and input these two variables into our multiplication function:
The above definition tells us to simply subtract from itself times for while . There is no problem since the number is subtracted times, despite it being negative. This is one of the ways we can say a negative times a positive number is negative (over the set of integers). However, this definition breaks down once we switch the roles of the number. Our next example shall attempt to prove a basic "theorem" most of us already know.
|
Proof 1: Prove that multiplying to , or for and given and , is equivalent to . First, we need to define what it means for a number to be negative. This is important to establish formally before we use it in our proof. Recall that one property of being a negative number is that it is the additive inverse of the magnitude of the number. That is, given a number , the additive inverse is . Also, a number must equal itself; this is by definition true. This is the property of equality, and it is important in establishing our theorem. Let us say we are trying to solve the problem . By the property of equality,
In (), notice how is a factor of both terms on the right hand side. This means that we may rewrite the equation as the following:
Recall that we defined the negative number to be the inverse operation. By the additive inverse property, . Therefore, we know . We know any number times zero equals zero since we proved this was true in the previous chapter. Ergo, we have a new property:
By an extension of the property of equality, whatever is done to one side of an equation requires it must be done to the other. From this property of integers, we may define simply this: From this, we have proved a positive times a negative integer equals a negative integer. |
A similar exercise can show that and . These two properties of multiplication allow us to keep the definition of multiplication the same for the set of integers. We will leave these two important "theorems" as non-trivial exercises for the reader.
Rational numbers start to break down the "repeated addition" idea of multiplication, since how can you add a number partially? Let us demonstrate the problem: Let and . Allow four numbers to be defined as an integer that are relatively prime to the other — , , , . Let and . If applied directly to our old definition, would be asking us to a strange operation: add a fraction to itself "fractionally" many times. This is strange indeed. While we will not be discussing how we determined this formal definition below, keep in mind it took mathematicians more than simply writing this as true to be accepted into our lexicon, today:
- .
The rational numbers definition does not contradict the old definition since each term therein is an integer, and thus, denominators for the terms are all . This means . We will skip defining real numbers since it involves introducing information that you will not learn unless you enter into some more pure math besides College Algebra or even Calculus.
This recursive addition defines a new operation, requiring us to define more and more specific cases. This idea of recursive addition can be extended to subtraction (which makes division) and then multiplication itself. Through recursive multiplication one reaches the idea of the exponent. As you have in the past referred back to properties of multiplication to help you operate expressions, you too will apply these ideas to learn about properties of exponents.
Definitions of Exponents (Form One)
editAs we referred to in the introduction to this page, exponent is an operation of repeated multiplication of the base over a period of times. The expression is often read aloud as to the power of . Allowing the function , in which and , to represent the exponent operation as follows,
will let us see what properties might exist for natural numbers. Over more clarifications, the power function, so to speak, will lead to rules.
Properties of Exponents (Under Form One)
editThe function for non-zero results in the following
The above result is true by definition although there is another way to think about this function. This type of thinking will be given later. For now, simply think this is true.
Given the two exponents and , multiplying the two gives the following:
|
Proof 2: for . This property of exponents can be proven by using the definition of exponent created herein. By definition, Therefore, in multiplying the two different functions, Because there are terms being multiplied to terms, every term therein has a base , and multiplication is associative, it is safe to infer there are terms of being multiplied together. As such, |
Given the two exponents and , dividing by for will give the following:
|
Proof 3: for and . Keep in mind that because we are working with natural numbers, . To keep everything in the natural numbers, this restriction must apply. Either way, let us continue by proving this property. By definition, In dividing the two different functions, Because there are terms being divided by terms of , every term therein has a base , and multiplication of the inverse operation is associative, it is safe to infer there are terms of after the division. This can further be shown through the operation as follows: all red terms are canceled and what is left over is the terms that are not canceled, . As such, |
Given the exponent operation , for any such that
- .
For any operation that results in , .
|
Proof 4: for and . This second-to-last rule has a pretty involved intuition behind it. Be sure to follow along: If , then . By the second bullet point above: Pay close attention to what this operation is telling us: there many constants multiplied to itself, for which this operation repeats times. Because factors of are multiplied again to itself as its operation many times, there of those factors in total. As such: |
Given the exponent operation , for any
- .
|
Proof 5: for . This will be the simplest proof in this chapter. All that will be needed is the definition of an exponent; specifically, the one that states the operation is simply repeated multiplication. We are given the following: Because multiplication is associative, From this, we learn that |
Qualifying the Definitions of Exponents
editApplying Exponents
edit
Polynomials
Polynomials
editA polynomial is an expression containing any number of variables and constants. The variables are combined by adding, subtracting, and multiplying. The variables themselves can be raised to a positive whole-number power.
Types
editA monomial is the product of any number of variables, each raised to any positive whole-number power. Thus, monomials do not involve addition or subtraction. Monomials may be multiplied by a constant.
These are all monomials:
A binomial is the sum of two monomials.
A trinomial is the sum of three monomials (or a binomial and monomial).
Simplifying
editSimplifying a polynomial (or "collecting like terms") is the process of reducing a polynomial to its shortest form. The number before a term is the term's coefficient. Add or subtract the coefficients of terms that have the same combination of variables. That is, add or subtract the coefficients of like terms.
To make communication of monomials easier, we oftentimes use the convention of writing the variables of each term in alphabetical order, and we use exponential notation so that in each term each letter appears only once. We like to put the number (the numerical coefficient) at the beginning of the term.
If the terms are each expressed in such a manner, we can quickly identify like terms. Two terms are "like" if, when you cover up the coefficient of each term, the rest of the terms are identical to one another.
We cannot combine "unlike" terms. That is, we leave them alone.
A polynomial must be simplified before it can be classified as a monomial/binomial/trinomial/polynomial.
Degree
editWe can talk about the degree of a term, or the degree of a polynomial for a certain variable. In this context, I am using "polynomial" to include monomials, binomials, and trinomials.
Most of the time, we talk about degree for polynomials that only contain one variable. In this setting, the degree of a single term is the exponent for the variable in that term. For example:
- The degree of is zero.
- The degree of is one.
- The degree of is five.
For a polynomial of a single variable, the degree of the polynomial is the largest exponent that appears on that variable. The degree of is three.
To find the leading coefficient of a polynomial, identify the numerical coefficient of the term having the largest degree.
The leading coefficient of is negative two.
(Remember, .)
To make things easier, we oftentimes like to write polynomials either in ascending or descending order.
Ascending order means that the degrees of the terms ascend (get bigger)
as you go from left to right,
and descending order means that the degrees of the terms descend (get smaller) as you go from left to right.
When we write
in descending order, we get .
If a polynomial is given in descending order, then the degree of the polynomial is the degree of the first term, and the leading coefficient is the number out front.
Check Your Understanding
editNote: these questions are going to be easy — they are not CLEP-type questions. As such, look at these as questions that can determine whether or not you understand the basics.
If you could answer all of these correctly. You understand the section and may move on.
Factoring
editCommon Factor
editFactoring polynomials deals with picking out the common factor. Just like before when we factored a real number we apply the same idea to binomials, trinomials, and other polynomials. We assume that you don't know how to factor variables, so we will introduce the concept by analyzing the question into smaller and smaller pieces to further understanding with the example problem below. For those who know how to do this, this may seem a little bit excessive, but it is important to fully understand what these type of problems means. Plus, in mathematics, when problems are very difficult, you break it down into easier pieces until you can finally tackle the big monster that is the problem.
|
Example 2.1.a: Factor the expression . Notice that each term in the expression has an with no coefficients. If you have not memorized exponent rules, please do! The reason for that memorization is to simplify the process. When multiplying two terms such that , the result of the expression is . Thus, you want to have some that when distributed onto every term in the parentheses, you get the same expression above. Let us set that up now:
While this seems like a complicated way to look at it, a simple tasked is asked of you. In short, . Because , each term in has the same basic structure. Ergo,
Here we have what the question is actually asking us to figure out: . Because is always equal to itself, yet the exponents are not, we may further rewrite the problem like so: Since is in the system of equations twice, it may be easier to eliminate from the system. In that case, multiply to the equation (2). After, add equation (1) to equation (2):
You could keep going, but you are going to find out some hard truths, and you probably have no time to waste getting every thing done. If you want a proof that what you are doing is futile, read the note.[Note 1.] What most problems mean by factoring an expression is to simply make it so that equation (3) is easy to solve. That is, let . From there: Because we allowed these two truths to exist, we can substitute these two values into the systems to find that . This option was very arbitrary (as you would have learned if you read note 1). Nevertheless, this is what most problems want you to do when factoring an expression with no coefficients. Allow to equal the smallest power value in the expression. Either way:
|
The biggest truth you should have learned is when factoring an expression with no coefficients, you are really being asked to find the greatest common factor, and you do that by factoring the variable in the problem to the smallest power value (highlighted in ). Here are a few examples:
But what about when factoring with coefficients. This is a little bit more complicated, but it works the same either way.
|
Example 2.1.b: Factor the expression . Here, we should be focusing on the coefficients before the exponents. If we were to do that, we would analyze this small problem first:
If you were to notice (or use a calculator), the largest value that is a factor of the numbers within is . Let us go ahead and factor that into our expression: The coefficients should not matter if you factor because when multiplying the expression , where is some constant, as per the associative property, . From there, multiplying one term by a constant does not matter: .* Therefore, we can apply the same general rule we discovered for Example 2.1.a: *Even if the other value is multiplied by another arbitrary constant , so long as the commutative property is a thing, . |
This procedure outlined above seems to work for any polynomial. Let's try it on a few:
We may now synthesize the information we learned from these two problems to outline a general procedure:
Given a polynomial with coefficients and variables, the following procedure should be followed.
- Find the greatest common factor for each of the coefficients.
- If there is no constant (a value that has no variable attached to it), factor the variable to the lowest power value in the expression. If there is a constant, simply keep the greatest common factor outside the parentheses.
You are now ready to fully factor any expression with a common term.
Grouping
editWhen there is no common term that travels throughout the entire polynomial you can factor by grouping. When factoring by grouping you need to split up the polynomial into two binomials.
|
Example 2.2.a: Factor the expression . Before we group, we need to do a quick check to see if we can factor the entire expression with just one term outside the parenthesis. If "4" was not a constant, we could factor the expression using the second step of the procedure. Another thing is that , which if we were to factor, that would mean that we are multiplying the same thing by 1, which is not very helpful. What are we to do then? We could factor by putting parts of the expression that have something similar together. This is harder to explain than do, so follow along with us. First, we are going to rewrite the expression. However, instead of keeping it black, we are going to recolor the expression with two groups of colors, red and green:
First, we are going to factor the red bit, . Notice that this part of the expression has a common factor . Factor that bit out and leave it to the side: From there we group the second binomial (in green) from the polynomial: . Notice the common factor is , so factor that bit: With these two bits factored, put them together; after all, they were part of the same expression:
|
Notice that we factored two binomials. Would it work if we were to factor a trinomial and then a binomial? We will answer that in a little bit. For now, try the next problem below, where we group polynomials with different variables.
|
Example 2.2.b: Factor the expression . As before, we need to do a quick check to see if we can factor the entire expression with just one term outside the parenthesis. First, , which if we were to factor, that would mean that we are multiplying the same thing by 1, which is not very helpful. However, because there is an inside the expression in some form, we could factor the entire expression like this:
We are not done however. Notice that you could still group the polynomial inside the parentheses with common terms. The may seem to complicate things; however, you can simply ignore it and say you are working on the inside of the parentheses. If you do get easily confused when too many things are on the paper or screen, it may be helpful to ignore them but always be sure to come back to them. Let us rewrite the expression inside of the parentheses in the same way we did in Example 2.2.a:
Looking at the red term , there is a common factor of with both terms, and , so we will factor outside the red term: As before, do the green term . Look at the coefficients and constants first: . We found a factor! As per the definition of constant, there is no variable and thus nothing to factor. Therefore, we can now factor that bit:
Finally, put everything together, including the term we ignored for a large part of the problem. In the spirit of not confusing the reader, the red and green parts will be placed inside the brackets "[]":
For the more astute readers, you may have noticed that is multiplied to each term inside the square brackets. In case you do not see it, let . If we were to replace the inside of the brackets like so (we are ignoring the colors since they are unnecessary for this part of the problem) we would notice that each term is multiplied by C, which is a factor of the expression and must be separated like so:
Remembering that we let , we substitute that back in and get
Finally, because of the associative property, we may ignore the large square brackets (but keep the parentheses because anything inside the parentheses must be done first before multiplying them: |
This problem was a little bit more involved than expected. Is there an easier way to do the green and red bits? Yes, and it is a method called F.O.I.L (Firsts, Outside, Insides, Lasts). Here is what we mean by foil (see right):

By remembering the foil method we can move backwards and solve this problem: .
We know that we multiply "firsts" with no coefficients. It is easier to :
- .
From there we go "outsides". We see that the first term is a multiple to the second term, , in the first binomial. So we get
- .
Next, "insides": we see is a multiple of . Therefore, we get
In fact, we are finished. Notice that "lasts" is , which gives us , the last term of the polynomial.
Keep in mind, this trick doesn't always work because the middle terms often end up having the same common variables and get simplified. It's helpful to start with the first terms and then go to the last terms. If you can get these two things you should be able to find the middle terms. Another thing to note is that we had to factor to make this work. While it could be possible to do the original problem like this, it is much easier to use FOIL when the last term does not have any variables. Before we move on to the next section, we must answer one final pressing question that we asked at the beginning of this section.
Factoring by grouping: a trinomial then a binomial? This question is fundamental to the curious student. Let us try it out using Example 2.2.a:
- .
Let us factor the trinomial: . Next, factor the monomial: . Now put them together:
- .
It seems to functionally work the same. In fact, it gives you the same answer. This should make sense because how you group anything does not change the answer (remember, associative property). However, it is standard mathematical syntax to factor a polynomial into two binomials. Because the CLEP exam is multiple choice, it should be easy to tell what the question is asking you to do. Either way, we have a procedure outlined for you again:
Given a polynomial with coefficients and variables, the following procedure should be followed.
- Find the greatest common factor for each of the coefficients.
- If there is no constant (a value that has no variable attached to it), factor the variable to the lowest power value in the expression. If there is a constant, simply keep the greatest common factor outside the parentheses.
- Group the polynomial into two binomials, and apply steps 1 and 2 to the different groupings. Do this separately for the two groupings.
- After completely factoring the two binomials. Put them together. If there is a common factor with the two combined binomials, factor it.
The procedure outlined above is best demonstrated in Example 2.2.b, and it does have a new: factoring by grouping. Simply look back at that example and apply each and every step onto that polynomial. Once you have done that, you now fully understand grouping polynomials.
Trinomials
editIt may seem strange to start factoring larger expressions only to then move back to the trinomial. However, there is a reason why the book is arranged the way it is. Trinomial factoring may be the most difficult aspect of the journey to, ultimately, solve equations involving degrees higher than 1. Nevertheless, this difficult concept is necessary for the college algebra student, especially for the next two sections of the "factoring" section.
As before, we will introduce the concept by exploring the consequences and behaviors that a mathematician may have first discovered techniques to solve. First, let us apply our algorithm and see if it applies to problems like these.
|
Example 2.3.a: Factor the expression .
Notice how our algorithm is confused at steps 3 and 4. Rightly, it should be because our algorithm assumes that we are factoring by grouping, which is not always applicable to all situations, such as this one. However, we can "force" the algorithm to fit into this situation. For example, we can try making the middle term split up into two terms. That is, we set , where
However, if we are to get anywhere with this, we want the middle term to have common factors. This is an interesting dilemma! Our ultimate end goal is to use the algorithm we have used previously on the trinomial above to get a factored form such the following is true:
However, notice how we got this result. If we want this to be factored, then must be a factor of this trinomial. The question is, what is ? This is the ultimate question. To answer this, we need to analyze this application of the algorithm carefully. Since is grouped together, we want to find a greatest common factor for and for . Ultimately, this means is the greatest factor of the grouped expression. Otherwise, it would be impossible to get as a factor of the expression. Therefore, . This tells us a very important truth about factoring the above expression:
This is a result of applying our algorithm! Using what we know, let us rewrite the above problem in terms of what we know: , where and . LOOK AT THIS! We can use a systems of equations! For. the purposes of saving time, we will skip through the process of finding those factors. This can be trivially done with a "guess-and-check," but a technique for finding this factor will be explained later. For now, just thank us when we tell you the factors are and . Using this result, we can now definitively use the same algorithm as before, but through some "fudging" or adjustments to the base expression we were solving for. Here is the process in action: |
Example 2.3.a showed us a very important algorithm that is taught all around the world. It is called the ac-method or the diamond method, the steps for which we will outline below.
Given a trinomial of the form , with , the following procedure should be followed.
- Find the greatest common factor for each of the coefficients.
- If there is no constant (a value that has no variable attached to it), factor the variable to the lowest power value in the expression. If there is a constant, simply keep the greatest common factor outside the parentheses.
- Find two values and whereby and .
- Rewrite the trinomial into the form ; then, group the polynomial into two binomials, and apply steps 1 and 2 to the different groupings. Do this separately for the two groupings.
- After completely factoring the two binomials. Put them together. If there is a common factor with the two combined binomials, factor it.
You should have realized by now that the ac-method is a modified version of the factoring by grouping method. This is why we decided to show factoring trinomials later, because the work involved is actually more than what you would expect from a carefully designed polynomial.
[More examples will be added later.]
Difference of Two Squares
editSo far in our factoring journey, we tried factoring general expressions that are not usually commonly seen. Despite that, there is a procedure that almost always works. Similarly, there are specialized cases in which a formula exists. It is the hope of this Wikibook that you understand why the formula is the way it is so that you may not simply blindly apply some seemingly unrelated relation.
Perfect Squares/Cubes
editExpanding
editDistribution
edit
Logarithms
Logarithms
editNatural Logarithms
editProperties
editChange of Base
edit
Functions
In math, it is often important to describe how a certain set of input from some certain operation can at some point represent the output of such operations. The tool math has created for this regard is called the function. The formal definition of a function can perhaps be a very tricky obstacle to grasp fully, and the best way to understand it is to perhaps use the intuitive concepts in practicum (as a preliminary step towards the goal, understanding). Therefore, we will begin this chapter by giving an intuition behind the processing.
The Intuitive Uses and Definition of Functions
editYou can think of a function as a kind of machine. You feed the machine raw materials (as an input), and the machine changes the raw materials into a finished product (the output). Let us describe a cook as a function. Handing a piece of lettuce to the cook would result in chopped lettuces as the output. The output is minced lettuces. A function in mathematics is somewhat equivalent. This viewpoint can get us far enough to at least understand its real-life applications.
|
Example 1.1(a): A function in everyday life 1 Think about dropping a ball from a bridge. At each moment in time, the ball has a velocity, . The velocity of the ball is a function of time. This type of function is called real-valued since the "finished product" is a number (or, more specifically, a real number). |
|
Example 1.1(b): A function in everyday life 2 Imagine the mean temperature of a river deviates everyday by . If the temperature of the river is sampled everyday, with samples per day, and the population mean of all the samples collected is while the deviation , then one way we can reflect the distribution of the temperature of the river is by using the Normal (or "Gaussian") function, which is written here below: If instead, the river only ever deviates from the mean, then one could write it in terms of absolute values: Either way, a function is used in everyday life. |
Think of a real-valued function as an input-output machine; you give the function an input, and it gives you an output which is a number (more specifically, a real number). For example, the squaring function takes the input and gives the output value . The same squaring function takes the input and gives the output value .
There are many ways which people describe functions. In the first example, a verbal descriptions is given (the height of the ball above the earth as a function of time). In the second example, some different operations of certain functions are given. The specifics of using operations to describe functions are given below:
- A function is given a name (such as ) and a formula for the function is also given. For example, describes a function. We refer to the input as the argument of the function (or the independent variable), and to the output as the value of the function at the given argument. (Note: more on this notation is described in the next section.)
- A function is described using an equation and two variables. One variable is for the input of the function and one is for the output of the function. The variable for the input is called the independent variable. The variable for the output is called the dependent variable. For example, describes a function. The dependent variable appears by itself on the left hand side of equal sign.
When a function is given a name (like in number 1 above), the name of the function is usually a single letter of the alphabet (such as or ). Some functions have names that are multiple letters (like the sine function .
Let us practice assigning a function using the second method described above by revisiting the first example again:
|
Example 1.1(c): The Ball's Velocity as a Function of Height Imagine, as a physicist, you were asked to describe the velocity as a function of height. Here is what may be best described (using energy equations):
The above information allows us to approximate the ball's velocity as a function of height:
|
The above equation is an example of a special type of function called a composite function. This function will be explained in much more detail later. For now, an intuition is all that is needed.
Hopefully, an intuition has begun forming inside the mind of the student. Let us see how to evaluate functions at certain inputs now.
|
Example 1.1(d): Inputs Given an Output. What is it? (Part 1) If we write , then we know that
Based on the above bullet points, the way to evaluate a function at a certain point is Therefore, the value of is
|
|
Example 1.1(e): Inputs Given an Output. What is it? (Part 2) Let us return to the function we derived in Example 1.1(c). With the function , where , we know the following is true:
When working with functions that is founded in real-life applications, it is important to also keep in mind units. Since SI units are used, and the gravitation constant is in meters per second-squared, the height will be in meters. We want to know what the velocity is if the ball is halfway between the bridge and the ground, . Assume . Let us begin evaluating the function: Therefore, the value of is
|
A Note on Notation
editFunctions are used so much that there is a special notation for them. The notation is somewhat ambiguous, so familiarity with it is important in order to understand the intention of an equation or formula.
Though there are no strict rules for naming a function, it is standard practice to use the letters , , and to denote functions, and the variable to denote an independent variable. is used for both dependent and independent variables.
When discussing or working with a function , it's important to know not only the function, but also its independent variable . Thus, when referring to a function , you usually do not write , but instead . The function is now referred to as " of ". The name of the function is adjacent to the independent variable (in parentheses). This is useful for indicating the value of the function at a particular value of the independent variable. For instance, if
- ,
and if we want to use the value of for when is equal to , then we would substitute for on both sides of the definition above and write
This notation is more informative than leaving off the independent variable and writing simply , but can be ambiguous since the parentheses next to can be misinterpreted as multiplication, . To make sure no person is confused by notation accidentally, follow this procedure:
- Define the function by equating it to some expression.
- Give a sentence like the following: "At , the function is..."
- Evaluate the function.
This procedure can change if the student is doing a multiple choice exam since communication is not important in that context.
Formalizing the Intuition
editAs of now, the definition below should not make too much sense. Read the definition so that you may see where the we gain the understanding of the mapping.
a mapping associating the elements of one set called the domain, , with the elements of another set called the range, , is a function. For each value we select from the domain of the function, there exists exactly one corresponding element in the range of the function.
For now, analyze the definition. Take notice at the implication of an element in the range being found through the correspondence of the element mapping from the domain. An example of how is given below.
|
Let function for all . For what value of gives ? In mathematics, it is important to notice any repetition. If something seems to repeat, keep a note of that in the back of your mind somewhere. Here, notice that and . Because is equal to two different things, it must be the case that the other side of the equal sign to is equal to the other. This property is known as the transitive property (always remember the Properties of Real Numbers): Next, simplify — make your life easier rather than harder. In this instance, since has as a like-term, and the two terms are fractions added to the other, put it over a common denominator and simplify. Similar, since is a mixed fraction, . Multiply both sides by the reciprocal of the coefficient of , from both sides by multiplying by it.
The value of that makes is .. |
Classically, the element "picked" from the domain is pictured as something that is fed into the function (the input) and the corresponding element in the range is pictured as the output. Notice the specificity of the language herein: an input is selected from the domain, meaning the domain is the set of all inputs; an output results from that specific input, meaning the range is the set of all possible outputs.
Since we "pick" the element in the domain whose corresponding element in the range we want to find, we have control over what element we pick and hence this element is also known as the "independent variable". The element in the range is beyond our control and is "mapped to" by the function. This element is hence also known as the "dependent variable", for it depends on which independent variable we pick. Since it is an element, the input is also known as the independent variable. Similar, the output is also known as the dependent variable.
The intuition of functions is better to grasp at first (for most students). However, the importance by which the formal definition of functions are to the foundations of algebra as we know it means that the formal definition should be viewed in high regards. Nevertheless, this does not mean that an intuition is unnecessary or even detrimental. Rather, students should be able to understand both viewpoints, and be able to relate them. As such, we argue that students should hold on to both viewpoints.
To recap, a function is a mapping of some element , called the domain, to exactly one element , called the range, such that . The image below should help explain the modern definition of a function:
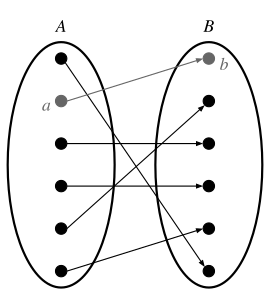
The Foundations of Functions: The Mapping, the Cartesian Cross Product, and Ordered Pairs
editNow that we understand the set, we will begin understanding the fundamental property of the function (the mapping). However, how do elements "map" to another set? It would be when the combination is "tied" to another element. Defining "tied" would be tricky without the help of sets. However, the set nicely defines tying, and it is through ordered pairs.
An order pair is defined to be a set written in the form of as:
- .
The logic in this is that the sets contained within are an element that is dependent on the order of the written pairs. Because uses both elements, the set gives the second coordinate based on the order of written pairs. However, this definition does not hold for , since it evaluates to give , which does not give an accurate reading of the second coordinate. However, this definition is good enough for the purposes of this textbook. Plus, the knowledge described herein is typically not taught in a College Algebra course.
Let and be two distinct sets. If we were to combine these two sets, it would be defined as the cartesian cross product (read aloud as cross ). is the set of ordered pairs whereby and :
- (read aloud as cross is the set that contains the ordered pair such that is in and is in . The wedge, is the logical symbol for "and").
The nature of the Cartesian Cross Product is hopefully self-evident. When two sets are combined as such, the ordered pair results. This is very close to the definition of the function. After all, the subset of this product is the function (for the most part).
Let and be two distinct sets. A mapping from to is a relation such that a subset of the cross product results in under the following conditions:
- For all and for all ,
- The ordered pairs and both in the subset
- Imply , and
- For all , there exists a such that .
The notation or is a condensed formatting of the definition (read aloud as maps into ).
All the above definition is saying is that given the cartesian cross product of the sets, called the domain and range, there exists a relation of the ordered pair that relates the domain to the range. For this book, the first notation () is preferred.
Finding New Properties of Functions Using Sets
editFrom the definitions above, new questions now arise. Here are the three main ones: can a function be (1) one-to-one? (2) many-to-one? (3) one-to-many? Consider each case.
- A function is considered one-to-one if an element from domain of function , leads to exactly one element from range of the function. By definition, since only one element is mapped by function from some element , implies that there exists only one element from the mapping. Therefore, there exists a one-to-one function because it complies with the definition of a function. This definition is similar to Figure 1.
- A function is considered many-to-one if some elements from domain of function maps to exactly one element from range of the function. Since some elements must map onto exactly one element , must be compliant with the definition of a function. Therefore, there exists a many-to-one function.
- A function is considered one-to-many if exactly one element from domain of function maps to some elements from range of the function. If some element maps onto many distinct elements , then is non-functional since there exists many distinct elements . Given many-to-one is non-compliant to the definition of a function, there exists no function that is one-to-many.
The modern definition describes a function sufficiently such that it helps us determine whether some new type of "function" is indeed one. Now that each case is defined above, you can now prove whether functions are one of these function cases. Here is an example problem:
|
Given: , where and are constant and . Prove: function is one-to-one. Notice that the only changing element in the function is . To prove a function is one-to-one by applying the definition may be impossible because although two random elements of domain set may not be many-to-one, there may be some elements that may make the function many-to-one. To account for this possibility, we must prove that it is impossible to have some result like that.
Assume there exists two distinct elements and that will result in . This would make the function many-to-one. In consequence, Subtract from both sides of the equation. Factor from both terms to the left of the equation. Multiply to both sides of the equation. Add to both sides of the equation. |
There are a few more important ideas to learn from the modern definition of the function, and it comes from knowing the difference between domain, range, and codomain. We already discussed some of these, yet knowing about sets adds a new definition for each of the following ideas. Therefore, let us discuss these based on these new ideas. The below definitions are a little confusing. The best way to interpret these is to draw an image. To the right of these definitions is the image that corresponds to it (including a formal definition of the corresponding definitions).

- The domain is defined to be a set with all elements mapping to at least one unique .
- The set of elements in and implies is the range of the function in the cartesian cross product, whereby the set of all elements maps to at least one unique element . That is, the range is the set of all elements that was mapped by some to one corresponding .
- The codomain is the set , where it is not necessarily the case that all elements was mapped by some . That is, the set of all elements found in is the codomain.
The abstract concepts can also be made less confusing by using a function that can put these concepts into more concrete terms. Assume there is a function whereby . Let this function be where . Let us write down what the domain, range, and codomain is for this particular function:
- Domain: or or simply . In this instance, the domain is the set of all elements of except , since this one cannot be mapped to some element in .
- Range: or or simply . In this instance, the range is the set of all elements of except , since this one cannot be mapped by some element in .
- Codomain: or or . This includes the one element that we were not allowed to map.
There is one more final aspect that needs to be defined. We already have a good idea of what makes a mapping a function (e.g. it cannot be one-to-many). However, three more definitions that you will often hear will be necessary to talk about: injective, surjective, bijective.

- A function is injective if it is one-to-one. That is, for and , if , then . Otherwise, it cannot be one-to-one. The same definition from before applies for one-to-one (realize that the definition of injective and one-to-one are the same).
- A function is surjective if it is "onto." That is, the mapping has as the range of the function, where the codomain and the range of the function are the same.
- A function is bijective if it is both surjective and injective.
Again, the above definitions are often very confusing. Again, another image is provided to the right of the bullet points. Along with that, another example is also provided. Let us analyze the function .
|
Given: , where is constant and . Prove: function is non-surjective and non-injective. Notice that the only changing element in the function is . Let us check to see the conditions of this function.
Is it injective? Let , and solve for . First, divide by . Then take the square root of . By definition, , so Notice, however, what we learned from the above manipulation. As a result of solving for , we found that there are two inputs, , that give the same output,. This means that for some individual that gives , there are two different inputs that result in the same value. Because when , this is by definition non-injective. Is it surjective? As a natural consequence of what we learned about inputs, let us determine the range of the function. After all, the only way to determine if something is surjective is to see if the range applies to all real numbers. A good way to determine this is by finding a pattern involving our domains. Let us say we input a negative number for the domain: . This seemingly trivial exercise tells us that negative numbers give us non-negative numbers for our range. This is huge information! For , the function always results for our range. For the set , we have elements in that set that have no mappings from the set . As such, is the codomain of set . Therefore, this function is non-surjective! |
Functions are an important foundation of mathematics. This modern interpretation is a result of the hard work of the mathematicians of history. It was not until recently that the definition of the relation was introduced by René Descartes in Geometry (1637). Nearly a century later, the standard notation () was first introduced by Leonhard Euler in Introductio in Analysin Infinitorum and Institutiones Calculi Differentialis. The term function was also an innovation during Euler's time as well, being introduced Gottfried Wilhelm Leibniz in a 1673 letter "to describe a quantity related to points of a curve, such as a coordinate or curve's slope." Finally, the modern definition of the function being the relation among sets was first introduced in 1908 by Godfrey Harold Hardy where there is a relation between two variables and such that "to some values of at any rate correspond values of ." For the person that wants to learn more about the history of the function, this page has been provided for you.
Summary of the Set Definitions of Functions
editThis section is perhaps the hardest to understand. A summary is provided before the end of the chapter to help students further their understanding.
- A cartesian cross product is the operation , where and are two distinct sets.
- A mapping is a relation denoted by , where and are two distinct sets, such that the cartesian cross product results in the ordered pair for any given to some unique .
- A function is a mapping of the set of all inputs, the domain, , to the set of all corresponding outputs, the range, such that for any , the cross product is true for one and only one .
- The element is an input. The entire set is the domain (since it comprises all inputs). For any but and gives . implies is the range if the cartesian cross product results in . The set is the codomain.
- Let . A function is injective when for all and , if , then . Symbolically, .
- A function is surjective if the mapping has as the range and codomain of the function. Put another way, if , then is said to be surjective if .
- A function is bijective if it is both injective and surjective.
The summary only uses jargon terms. For the student that was able to understand and translate the jargon, they are ready to move on to the "Check your understanding." It is in the student's best interest to understand this section because the terms will come back again so that students may fully appreciate the intuition behind composite functions and inverse functions, which we will define in due time. Plus, these definitions are sometimes necessary for proofs. Having a good understanding of these basic foundations of functions will be helpful for the student throughout math, even for students who are not math majors.
Remarks
editThe following arise as a direct consequence of the definition of functions:
- By definition, for each "input" a function returns only one "output", corresponding to that input. While the same output may correspond to more than one input, one input cannot correspond to more than one output. This is expressed graphically as the vertical line test: a line drawn parallel to the axis of the dependent variable (normally vertical) will intersect the graph of a function only once. However, a line drawn parallel to the axis of the independent variable (normally horizontal) may intersect the graph of a function as many times as it likes. Equivalently, this has an algebraic (or formula-based) interpretation. We can always say if , then , but if we only know that then we can't be sure that .
- Each function has a set of values, the function's domain, which it can accept as input. Perhaps this set is all positive real numbers; perhaps it is the set {pork, mutton, beef}. This set must be implicitly/explicitly defined in the definition of the function. You cannot feed the function an element that isn't in the domain, as the function is not defined for that input element.
- Each function has a set of values, the function's range, which it can output. This may be the set of real numbers. It may be the set of positive integers or even the set {0,1}. This set, too, must be implicitly/explicitly defined in the definition of the function.

The vertical line test
editThe vertical line test, mentioned in the preceding paragraph, is a systematic test to find out if an equation involving and can serve as a function (with the independent variable and the dependent variable). Simply graph the equation and draw a vertical line through each point of the -axis. If any vertical line ever touches the graph at more than one point, then the equation is not a function; if the line always touches at most one point of the graph, then the equation is a function.
(There are a lot of useful curves, like circles, that aren't functions (see picture). Some people call these graphs with multiple intercepts, like our circle, "multi-valued functions"; they would refer to our "functions" as "single-valued functions".)
Linear Equations
Linear Equations
editLinear equations are in the form:
a is the slope, b is the y-intercept.
They may be in the form:
Linear Inequalities
edit
Quadratic Equations
Quadratic Equations
editQuadratic equations take the form:
They can have zero, one, or two real solutions.
Quadratic Inequalities
editThe Quadratic Equation
editTo solve any quadratic equation in the standard form, use:
Absolute Value Equations
Absolute Values
editAbsolute Values represented using two vertical bars, , are common in Algebra. They are meant to signify the number's distance from 0 on a number line. If the number is negative, it becomes positive. And if the number was positive, it remains positive:
For a formal definition:
This can be read aloud as the following:
If , then
The formal definition is simply a declaration of what the function represents at certain restrictions of the -value. For any , the output of the graph of the function on the plane is that of the linear function . If , then the output is that of the linear function .
For our purposes, it does not technically matter whether or . As long as you pick one and are consistent with it, it does not matter how this is defined. By convention, it is usually defined as in the beginning formal definition.
Please note that the opposite (the negative, -) of a negative number is a positive. For example, the opposite of is . Usually, some books and teachers would refer to opposite number as the negative of the given magnitude. For convenience, this may be used, so always keep in mind this shortcut in language.
Properties of the Absolute Value Function
editWe will define the properties of the absolute value function. This will be important to know when taking the CLEP exam since it can drastically speed up the process of solving absolute value equations. Finally, the practice problems in this section will test you on your knowledge on absolute value equations. We recommend you learn these concepts to the best of your abilities. However, this will not be explicitly necessary by the time one takes the exam.
Domain and Range
editLet whose mapping is . By definition,
- .
Because it can only be the case that and , it is not possible for . However, since has no restriction, the domain, , has no restriction. Thus, if represents the range of the function, then and .
Let whose mapping is represent the absolute value function. If is the domain and is the range, then and .
By the above definition, there exists an absolute minimum to the parent function, and it exists at the origin,
Even or odd?
editRecall the definition of an even and an odd function. Let there be a function
- If and , then is even.
- If and , then is odd.
|
Proof: is even Let . By definition,
Suppose . Let . |
Because is even, it is also the case that it is symmetrical. A review of this can be found here (Graphs and Their Properties).
One-to-one and onto?
editRecall the definitions of injective and surjective.
- If , and , then is injective.
- If for all there is an such that , then is surjective.
|
Proof: is non-injective Suppose and . By the previous proof, we showed is even. As such, we can use the value to make the following statement: Therefore, is non-injective. |
Because we have not established how to prove these statements through algebraic manipulation, we will be deriving properties as we go to gain a further understanding of these new functions. Establishing whether a function is surjective is simply through checking the definition (negating if otherwise to establish it as non-surjective).
|
Proof: is non-surjective Suppose . There exists an element , for which for all . |
A review of the definitions can be found here (Definition and Interpretations of Functions).
Intercepts and Inflections of the Parent Function
edit
With all the information provided from the previous sections, we can derive the graph of the parent function . It is even, and therefore, symmetrical about the -axis since there is an -intercept at . Finally, because we know the domain and range, we know the minimum of the function is at , and we know the definition of the function, we can easily show that the graph of is the following image to the right (Figure 1).
A summary of what you should see from the graph is this:
- Domain: .
- Range: .
- There is an absolute minimum at .
- There is one -intercept at .
- There is one -intercept at .
- The graph is even and symmetrical about the -axis.
- The graph is non-injective and non-surjective.
- The graph has no inflection point.
Transformations of the Parent Function
editMany times, one will not be working with the parent function. Many real life applications of this function involve at least some manipulation to either the input or the output: vertical stretching/contraction, horizontal stretching/contraction, reflection about the -axis, reflection about the -axis, and vertical/horizontal shifting. Luckily, not much changes when it comes to the manipulation of these functions. The exceptions will be talked about in more detail:
Let and . There must be an . Thus,
- If , then is an expansion of by a factor of .
- If , then is a contraction of by a factor of .
- If , then is a reflection of about the -axis.
Let and . There must be an . Thus,
- If , then is an upward shift of by .
- If , then is a downward shift of by .
Let and . There must be an . Thus,
- If , then is a leftward shift of by .
- If , then is a rightward shift of by .
The properties not listed above are exceptions to the general rule about functions found in the chapter Algebra of Functions. The exceptions are not anything substantial. The only difference with what we found generally versus what we have provided above are simply a result of what we found in the previous section.
- There is no reflection about the -axis because the function is even and symmetrical.
- There is no horizontal expansion and contraction because it gives the same result as vertical expansion and contraction (this will be proven later).
We now have all the information we will need to know about absolute value functions now.
Graphing Absolute Value Functions
editThis subsection is absolutely not optional. You will be asked these questions very explicitly, so it is a good idea to understand this section. If you didn't read the previous subsection, you are not going to understand how any of this makes sense.
Fortunately, the idea behind graphing any arbitrary function is mostly dependent on what you know about the function. Therefore, we can easily be able to graph functions. These examples should hopefully be further confirmation of what you learned in Algebra of Functions.
|
Example 1.2(a): Graph the following absolute value function:
This method will work for any arbitrary function. However, it will not always be the quickest method for absolute value functions. We follow the following steps. Let be the parent function and .
Since has , , , and , we may apply these steps as given to get to our desired result. As this should be review, we will not be meticulously graphing each step. As such, only the final function (and the parent function in red) will be shown.
While method 1 will always work for any arbitrary, continuous function, method 3 is fastest for the absolute value function that composes a linear function. First, we should try to find the vertex. We know from Algebra of Functions that the only thing that will affect the location of the vertex in even functions is the term on the inner composed linear function and the vertical shift of the entire function, . Rewriting the absolute value equation as shown below will allow us to find the vertex of the function. This then tells us the vertex is at . This method then tells us to graph the slopes. However, how should that work? Recall the formal definition of an arbitrary absolute value function: In the above definition of a general absolute value function, . This means that where the -value implies a vertex on the function, that is how we restrict absolute value function. In our instance, , for which , so . We can say, thusly, that
To be continued. |
Practice Problems
edit
Absolute Value Equations
editNow, let's say that we're given the equation and we are asked to solve for . What number would satisfy the equation of ? 8 would work, but -8 would also work. That's why there can be two solutions to one equation. How come this is true? That is what the next example is for.
|
Example 2.0(a): Formally define the function below: Recall what the absolute value represents: it is the distance of that number to the left or right of the starting point, the point where the inner function is zero. Recall the formal definition of the absolute value function: We want to formally define the function . Let First, we need to find where . From that, it is safe to say that the following is true: |
It is important to know how to do this so that we may formally apply an algorithm throughout this entire chapter. For now, we will be exploring ways to solve these functions based on the examples given, including the formalizing of an algorithm, which we will give later.
The above example demonstrates an algorithm that is commonly taught in high schools and many universities since it applicable to every absolute value equation. The steps for the algorithm will now be stated. Given :
- Isolate the absolute value function so that is equal to another function, or .
- Write the equation so that you solve for the composed function into two such cases. Given ,
- Solve for and
- Solve for .
A basic principle of solving these absolute value equations is the need to keep the absolute value by itself. This should be enough for most people to understand, yet this phrasing can be a little ambiguous to some students. As such, a lot of practice problems may be in order here. We will be applying all the steps to algorithm outlined above instead of going through the process of formally solving these equations because Example 1 was meant to show that the algorithm is true.
|
Example 2.0(c): Solve for : We will show you two ways to solve this equation. The first is the standard way, the second will show you something not usually taught. Standard way: Multiply the constant multiple by its inverse. We'd have to divide both sides by to get the absolute value by itself. We would set up the two different equations using similar reasoning as in the first example: Then, we'd solve, by subtracting the 6 from both sides and dividing both sides by 2 to get the by itself, resulting in . We will leave the solving part as an exercise to the reader. Other way: "Distribute" the three into the absolute value. Play close attention to the steps and reasoning laid out herein, for the reasoning for why this works is just as important as the person using the trick, if not moreso. Let us first generalize the problem. Let there be a positive, non-zero constant multiple multiplied to the absolute value equation : Let us assume both are true. If both statements are true, then you are allowed to distribute the positive constant inside the absolute value. Otherwise, this method is invalid! Notice the two equations have the same highlighted answer in red, meaning so long as the value of the constant multiple is positive, you are allowed to distribute the inside the absolute value bars. However, this "distributive property" needed the property that multiplying two absolute values is the same as the absolute value of the product. We need to prove this is true first before one can use this in their proof. For the student that spotted this mistake, you may have a good logical mind on one's shoulder, or a good eye for detail.
By confirming the general case, we may be employ this trick when we see it again. Let us apply this property to the original problem (this gives us the green result below): This all implies that From there, a simple use of algebra will show that the answer to the original problem is again . |
Let us change the previous problem a little so that the constant multiple is now negative. Without changing much else, what will be true as a result? Let us find out.
|
Example 2.0(d): Solve for : We will attempt to the problem in two different ways: the standard way and the other way, which we will explain later. Standard way: Multiply the constant multiple by its inverse. Divide like the previous problem, so the equation would look like this: . Recall what the absolute value represents: it is the distance of that number to the left or right of the starting point, zero. With this, do you notice anything strange? When you evaluate an absolute value, you will always get a positive number because the distance must always be positive. Because this is means a logically impossible situation, there are no real solutions. Notice how we specifically mentioned "real" solutions. This is because we are certain that the solutions in the real set, , do not exist. However, there might be some set out there which would have solutions for this type of equation. Because of this posibility, we need to be mathematically rigorous and specifically state "no real solutions." Other way: "Distribute" the constant multiple into the absolute value. Here, we notice that the constant multiple . The problem with that is there is no such that . The only way this would be true is for because With this property, we may therefore only distribute the constant multiple as with a negative as a factor outside the absolute value. As such, It seems the other way has us multiply a constant by its inverse to both sides. Either way, this "other method" still gave us the same answer: there is no real solution. |
The problem this time will be a little different. Keep in mind the principle we had in mind throughout all the examples so far, and be careful because a trap is set in this problem.
|
Example 2.0(e): Solve for : There are many we ways can attempt to find solutions to this problem. We will do this the standard and allow any student to do it however they so desire. Because the absolute value is isolated, we can begin with our generalized procedure. Assuming , we may begin by denoting these two equations:
These are only true if . For now, assume this condition is true. Let us solve for with each respective equation: Equation () Equation () We have two potential solutions to the equation. Try to answer why we said potential here based on what you know so far about this problem. Why did we state we had two potential solutions? Because we had to assume that and is true for the provided . Because of this, we have to verify the solutions to this equation exist. Therefore, let us substitute those values into the equation:
This equations has no real solutions. More specifically, it has two extraneous solutions (i.e. the solutions we found do not satisfy the equality property when we substitute them back in). |
Despite doing the procedure outlined since the first problem, you obtain two extraneous solutions. This is not the fault of the procedure but a simple result of the equation itself. Because the left-hand side must always be positive, it means the right-hand side must be positive as well. Along with that restriction is the fact that the two sides may not equal the other for the values whereby only positive values are given. This is all a matter of properties of functions.
|
Example 2.0(f): Solve for : All the properties learned will be needed here, so let us hope you did not skip anything here. It will certainly make our lives easier if we know the properties we are about to employ in this problem. Looking at the second equation might be the first declaration of absurdity. However, an application of the fundamental properties of absolute values is enough to do this problem.
Peel the problem one layer at a time. For this one, we will categorize equations based on where they come from; this should hopefully explain the dashes: 3-1 is first equation formulated from (), for example.
We can demonstrate that some equations are equivalents of the other. For example, () and () are equivalent, since dividing both sides of () by gives (). Further, () and () are equivalent (multiply both sides of equation () by ). After determining all the equations that are equivalent, distribute to the corresponding parentheses.
Now all that is left to do is solve the equations. We will leave this step as an exercise for the reader. There are two potential solutions: . All that is left to do is verify that the equation in the question is true when looking at these specific values of :
Because both solutions are true, the two solutions are . |
Absolute value equations can be very useful to the real world, and it is usually when it comes to modeling. We will introduce one example of a standard modeling problem, then one unusual application in geometry (EXAMPLE WIP).
The next problem typically requires some trigonometry to solve easily. However, with one extra piece of information, one can use the properties of the absolute value property to solve the following problem.
|
Example 2.0(h): Tiling a Roof (adapted from Trigonometry Book 1)  An engineer is planning to make an roof with a m. frame base and m. perimeter. The angle of the slope of the roof to the base is . The sloped sides are congruent. A reference image (Figure 2) of the sloped-roof (with no cartesian plane) is provided. Given the area of a triangle is , and the distance formula is , find the area of the triangular cross section of the roof. Answer  Explanation The following problem requires you to think about what doesn't change to successfully allow you to determine what one situation allows for all of the following to be possible. We will apply our problem-solving steps derived onto this problem first before we discuss one difference in this problem that somewhat breaks our algorithm. We will draw it first.
We can gain a lot of information from Figure 3.
Our drawing helped us gleam a lot of information. Knowing the perimeter is tells us that the distance is However, Figure 3 tells us that . Therefore, by the transitive property, After knowing the vertical contraction, we can determine the height of the triangle. From there, the area. The area of the triangle is therefore, |
Notice how it was not necessary for us to solve for a specific value of based on the absolute value equation. The only aspect of absolute value equations necessary for this problem is the graph properties and some logic. In a way, this is the most easy absolute value problem. However, the needed creativity for it makes up for the "easiness" of the problem.
Practice Problems
edit
Inequalities with Absolute Values
editIt is important to keep in mind that any function can be less than any other function. For example, has any solutions for . So long as the value for is within that range, the function is less than the output of . The algebra for inequalities of requires a bit more of demonstration to understand. While the methods we use will not be proven, per se, our examples and explanations should give a good intuition behind the idea of find the inequalities of absolute values.
|
Example 3.0(a): First, let us simplify the following expression through the method we demonstrated in the previous section (factoring the inside of the absolute value and bringing the constant out). Keep in mind, since we are switching the sides for which we view the equation, 50 is the left instead of right, we must also "flip" the inequality to be consistent with the original equation. From there, it should be easy to see that Let us further analyze this situation. What the above equation is saying is is less than the function . We want to make sure the inside value is less than five. Because the absolute value describes the distance, there are two realities to the function. Let Because there are two "pieces" to the function , and we want each piece to be less than 5,
We will demonstrate the more common procedure in the next example. For now, this intuition should begin to form an idea of algebraic analysis. We will solve the left-hand then the right-hand case.
We have found a possible distribution of values that allows the following equation to be true, where , and it is for values of in between and , non-inclusive. |
The above example is an intuition behind how solving for inequalities work. Technically speaking, we could make a proof for why we have to "operate" (take the steps seen above) absolute value inequalities this way. However, this will be a little too technical and involve a lot of generalization that could potentially confuse students rather than enlighten. If the student feels the challenge is worth, then one may try the proof of the steps we derived below. This is considered standard procedure (according to many High School textbooks).
- Simplify until only the "absolute value bar term" is left.
- Solve by taking the inside and relating it by the inequality for the "left-hand" values; taking the same expression found inside the absolute value, for the "right-hand" equation, negate the related term and flip the inequality to then solve.
- Rewrite into necessary notatioon.
Although the procedure may seem to be confusing, we are really only trying to make the algorithm as specific as possible. In reality, we will show just how easy it is to apply this algorithm for the problem above.
|
Example 3.0(a) (REPEAT): Let us skip to the most simplified form. Now let us apply the above algorithm.
From there, we will solve.
|
There are two possible reasons why this procedure exists. For one, it allows us to quickly solve for in the "right-hand" equation without the need for double the amount of multiplications necessary to solve for (it lessens the amount of times we have to flip the inequality). Next, it allows us to focus more on the idea behind absolute value equations (the value inside will be positive, and hence, we want to find all values that allow us to find all possible solutions).
Nevertheless, keep in mind how we found this procedure, and it was through applying the function definition of absolute values. In reality, we did the exact same thing for absolute value equations. The only difference in application of algorithm applies to the inequality, which further "complicates" matters by introducing a new concept to the non-injective absolute value function. Through finding two solutions, we gave two possible ranges for values of .
Hopefully, this example should further shine a light into what many high schoolers think to be "black magic" among finding solutions to absolute value inequalities and equalities. The next examples should only hopefully further the concepts learned. Keep in mind, if one does not like the algorithm presented in the repeat example above, one is perfectly fine to use the other algorithm. The benefit of multiple choice is the ability to use any method, and only the correctness of your answer will be considered.
|
Example 3.0(b): Explanations given later |
|
Example 3.0(c): Explanations given later |
|
Example 3.0(d): Explanations given later |
Introduction to example included later.
|
Example 3.0(e): Variable temperature problem Problem: The temperature in a room averages at around in the summer without air conditioning. The change in temperature is dependent on the ambient weather conditions. Without air conditioning, the maximum change in temperature from the average is . When the air conditioning is on, the temperature of the room is a function of time (in hours), given by . The maximum deviation in temperature should be no more than .
Answers:
Explanation: When working with word-problems it is best to rewrite the problem into something algebraic or "picturesque" (i.e. draw the problem out). One can also use both, as we will soon do.  The benefit of drawing a picture (or, more accurate, a sketch) of the situation is being able to more easily interpret situations. We are highly visual people, after all, so seeing a picture is a lot easier to understand than words. The highly intuitive nature of geometry also lends itself well to algebraic interpretations. Let us reread the situation without A/C.
This gives us a lot of information. We know that and , so to keep it as one singular equation, it is best to write it as an absolute value equation. For this situation,
It is important to know why this is true. Recall the absolute value represents the distance from for the inside value. If is the reference point, then to get from , you need to subtract 20 from the current value . As such, this equation is true. Now let us look at the situation for the air conditioning.
Based on the wording of the sentence, the temperature is based on the time, and the temperature can only be at most from the average. By the same logic given for Equation (),
Equation () is left in the same form to show how similar the two equations are, and to also relate more to the wording of the set-up text. Using the transitive property, one can simplify the equation further to obtain
Recall how , where . Because of this property, one can simplify the equation further to obtain the final equation for part (a):
This sufficiently answers item (a), perhaps the hardest part in the question. However, with the two equations obtained, () and (), we can answer both items (b) and (c). Let us reread parts (b) and (c) using our understanding of the question:
This is, in essence, asking the examinee to find the value of using (). The previous examples should have hopefully prepared you with solving for absolute value inequalities.
Since the problem is asking for the minimum temperature value, , of an ambient temperature room, the correct answer here is . Keep in mind, we are allowed to put that equal sign there thanks to the problem's wording ("at most" implies less than or equal to). Also, always remember to put units in word problems.
This is, in essence, asking the examinee to find the value of time (in hours) using the most simplified equation, Equation ().
Because, in essence, only the positive case is considered (we are only looking at time ), the maximum amount of time that the air conditioning will allow is hours. |
Lesson Review
editAn absolute value (represented with |'s) stands for the number's distance from 0 on the number line. This essentially makes a negative number positive although a positive number remains the same. To solve an equation involving absolute values, you must get the absolute value by itself on one side and set it equal to the positive and negative version of the other side, because those are the two solutions the absolute value can output. However, check the solutions you get in the end; some might produce negative numbers on the right side, which are impossible because all outputs of an absolute value symbol are positive!
Lesson Quiz
edit
Sequences and Series
In mathematics, it is important to find patterns. That is what mathematicians do almost everyday of their lives. How they determine patterns is different depending on the type of mathematics they work with. For college algebra, determining patterns is part of the curriculum. The problem below demonstrates one way we determine these patterns. Keep in mind that the problem below is an Exploration and most likely not representative of the types of problems you may see in the CLEP College Algebra exam.
Concatenating the letter to will give us a new letter, . Adding this to the "Old Alphabet" obviously does not make it the old set anymore, so let us define the alphabet in which you add new letters to the old one the "New Alphabet" How many of the new letters are in this set? Well, each letter from "Old Alphabet" must get another additional letter to make the "New Alphabet" Therefore, for each letter, letters are added to the old one (i.e. the letter "A" will have letters "A", "B", "C",...,"Z" concatenated to "A", so 26 more letters are added to each letter of the "Old Alphabet"). Since each letter is used, exactly are created in the "New Alphabet" The figure below may help demonstrate this new fact.
The left brace tells us how many letters are in the "Old Alphabet"; the top brace for each "row" tells us how many new letters are created per letter of the alphabet. Since 26 letters are created for each letter of the "Old Alphabet," add every new letter created into this subset of the "New Alphabet." Since there are rows, and each row creates new letters,
Remember that there are still 26 other letters in the "old alphabet" not included in the figure above. As such, add 26 to the answer above to get the total number of letters in the New Alphabet.
Given that we know the total number of letters in the "New Alphabet," we can find out what position letter HY is in this subset of the "New Alphabet." First, the letter position of H is . Second, the letter position of Y is . Since the above figure shows a table, we can find HY by looking up that "coordinate." Since the position of HY contains all the terms in that given area, we can multiply the two values to get the area (i.e. it is a rectangle that contains all those letters). This is not the final answer, however. Realize that we excluded some other letters by multiplying in that block and subset; ergo, the position of the letter is
What were we doing in the problem above? Essentially, we were simply trying to find what position some "term" is in. Does it not intrigue you to see math try to find a position of some "term" in a list? We have problems like these as mathematicians because the patterns underlying a "list" of numbers can help us determine new facts of mathematics. After all, what were we doing when using functions? We were trying to find a number using a pattern (the function). Unlike the previous sections, however, we were not given a formula. Luckily enough, it is not difficult to make a formula for a given "list" of numbers. Before we dive into these new problems. It helps to establish definitions.
A sequence is a list of elements, such as numbers, figures, or letters, that is generally written in some pattern.
A term is an item found within a sequence.
There is a little disclaimer to get out of the way before we try to solve some problems. First, a sequence can have no pattern. However, for our purposes, we will not count any list of numbers in which no pattern exists. Second, even in simple sequences, numbers of any kind can be named if they follow after a sequence rule. For example, here's a sequence in which the rule is to list prime numbers: If you were like most people, you would probably name the prime numbers in order. However, you could perhaps finish the sequence like this: For our purpose of standardization, we will follow a pattern by stating what number you must find first or identify the pattern.
Let's begin exploring the world that is Sequences and Series.
Sequences
editAs you already know, a sequence is a list of objects that generally follow a pattern. However, the type of pattern that is described will classify sequences into either arithmetic sequences or geometric sequences. Each will be explored in depth within the next sections.
Arithmetic Sequences
editAn index is the location of a term within a sequence, usually denoted by or .
An arithmetic sequence is a sequence in which an added real number , called the difference, is added to each successive term, except the first term, , such that the sequence forms in a one-to-one correspondence.
An example could perhaps help you figure with the formal definition above: The sequence has a one-to-one correspondence with the general sequence since the first term , second term , third term , and so on. The difference is the amount added to each previous term to get the new term. For , or . Solving for is the difference of the two terms. In this example, the difference is . This is how we define an arithmetic sequence.
Recursive Formula
editOften times, we want to generate a sequence using a formula (we are mathematicians, after all, and we like to study sequences to see if there are any general patterns). If we want to find , we may use the following formula:
However, the above formula could describe any sequence that has that general pattern. To fix this, we need to describe the first term as well when using the formula above. There are two ways to describe this formula:
- We have it horizontally deliniated: .
- We have it vertically deliniated:
To save space, we will horizontally deliniate formulas for arithmetic sequences in this WikiBook.
Formulas in which the first term is identified along with an equation in which the previous term is added by to get the next term is called a recursive formula.
A recursive formula is a formula that describes how to get a term or many terms of a sequence by stating the starting value or values and each previous term or terms and adding difference to each subsequent term.
Given an initial value and constant difference , the th term in an arithmetic sequence is given by the previous th term of the sequence:
- OR
|
Example 1.1.1.a: Find the th term to the arithmetic sequence To determine the next term, we first need to find the difference . Note that an arithmetic sequence will have the next term add to the previous term. Since that is how the arithmetic sequence works, is a valid way to find the difference between two terms. Solving for , we find the constant difference is . Since the difference is the same for each given term in the sequence, we can find the 7th term by adding to , which gives us . Finally, add to the next term to get the final answer: |
There are many reasons why it is more important to have a recursive formula. It is not always slow; it may be easier to understand. The next example shows why this is exactly true
|
Example 1.1.1.b: Write the recursive formula to the sequence . Many of you will perhaps know this famous pattern as the Fibonacci Sequence. For those of you who do not know this sequence, the way we determine the next term is by using the previous terms and adding them together. In our notation, we would say that the term at index , is equivalent to . Remember, however, we are not done. If a mathematician saw the sequence , he (or she) would determine that also describes that sequence. Therefore, we must list the first two terms because listing only the first term would not allow us to get the next term. This means our final answer is |
Note that Example 1.1.b is not an example of an arithmetic sequence. Your next exploration will be to determine why this is true. Along with that, you will use your critical thinking skills to argue for or against something in the explorations after that one.
- Argue either for OR against the claim that the recursive formula is arithmetic and recursive.
- If you disagree that is arithmetic and recursive, write a formula that is arithmetic and recursive.
- If you agree that is arithmetic and recursive, explain why it is so.
Finally, if , , and ,
- argue either for OR against the idea that the formula is arithmetic and recursive.
Direct Formula
editBy now, you may be wondering if there is a way to find the term of an arithmetic sequence directly. Well, there is. Before giving you the formula, let us go through the motions for our general recursive arithmetic formula . Let's chart the recursive arithmetic formula.
If you think about it, the table above is basically a linear function, although starting at instead of . Write out the function as . We get near our answer. Our independent variable is horizontally translated by to the right, so is our function. In fact, we found our direct relationship. Rewrite it the way we normally write it and we found our direct formula: .
A direct formula describes how to get a term or many terms of a sequence by only using a formula that directly finds a particular value, without stating the first term or terms of a sequence.
Given an initial value and constant difference , the th term in an arithmetic sequence is given by the direct formula:
|
Example 1.1.2.a: An arithmetic sequence is discovered. What is the th term in the sequence? As always, before we can determine the answer, we need to find the "rate of change" of our sequence. Since , we know that . The second term is , so when , . Of course, now we can solve for :
Since we now know the common difference, we can find the smallest th term in the sequence. By using our direct formula for an arithmetic sequence, we can find the index in which it is possible. Since , we find the th term by substituting . Ergo, . Solve for to get the final answer.
|
The example above would be a routine, straightforward problem in the CLEP College Algebra exam. However, as practice makes perfect, we will also have non-routine problems that involve thorough understanding of the topic and concepts and skills learned, which will make up 50% of the exam. This is why it is important to do the explorations. While they may not be on a CLEP exam, they are vital in making you think like a mathematician. The next problem will be non-routine problem.
|
Example 1.1.2.b: What is the smallest index needed to find a negative term in the arithmetic sequence ? As always, before we can determine the answer, we need to find the "rate of change" of our sequence. Since , we know that . We know that the second term is , so when , . Of course, now we can solve for :
Since we now know the common difference, we can find the smallest term needed to reach a negative number in our sequence. By using our direct formula for an arithmetic sequence, we can find the index by solving for . Since , we find the minimal index in which it is possible to have a number less than zero. Ergo, . Now all we have to do is solve for .
Since index must be greater than , the minimal index required to find the term that is negative is at |
CLEP Practice Problems: Check Your Understanding
edit
Geometric Sequence
editA geometric sequence is a sequence in which a multiplied real number , called the common ratio, is multiplied to each successive term, except the first term, , such that the sequence forms
As always, if you are unable to understand, try a few examples of numbers to think of in your head. Let the common ratio and let . The next term , so . If you keep the pattern going for each term of the sequence, you would get the following:
Recursive Formula
editAs with the arithmetic formula, you can find the recursive formula and the direct formula for a geometric sequence. Since every term is multiplied by common ratio , let any term of index be represented by . To find the next term requires knowing the previous term. Ergo,
Given an initial value and constant difference , the th term in an arithmetic sequence is given by the previous th term of the sequence:
- OR
Direct Formula
editAs with the arithmetic sequence, Let us chart the recursive geometric formula. .
If you think about it, the table above is basically an exponential function, , starting at . Write out the function as . We get near our answer. Our independent variable is translated to the right unit, so is our function. In fact, we found our direct relationship. Rewrite it the way we normally write it and we found our direct formula: .
Given an initial value and common ratio , the th term in an geometric sequence is given by the direct formula:
|
Example 1.2.2.a: A geometric sequence is discovered. What is the th term in the sequence? To find the answer, we need to know the common ratio of the sequence above. Pick any arbitrary term in the sequence and apply it to the direct geometric formula: . Find : Knowing the value of , you can find the th term in the sequence by using the direct formula: |
As always, these examples are things you can work through yourself or follow along so that you can see how to do a problem.
- multiply each value of by a common ratio . Determine whether the range will also be a geometric sequence through example using any value of .
- prove that multiplying the domain, , by a common ratio will give a range that is geometric (where the common difference for the domain is .
- The question is asking whether or not will give a range for such that you multiply by a constant. Let's define that constant as . Let . Since , if , then . Since , function . Since any term will give , function . Since , function . Since and are constant, the expression will be constant. Since you are multiplying the range, , by a common ratio (otherwise known as a geometric sequence), given the constant , then when multiplying the values of the domain, the range must be multiplied by a constant:
Series
editIt is great to find these patterns to these sequences, but is that the only use we have for these sequences? As always, the answer in math is never no in regards to a low amount of utility (i.e. usefulness). A function does not only describe the pattern associated with numbers but also predicts the graph created when plotted using for its inputs and for its outputs. Using the terms of a sequence, can we determine a sum? We can, and it is called a series.
A series is the sum of the terms of a sequence.
There is always a way to find the sum of a sequence by force: add up the terms one by one and get the answer. Mathematicians are lazy people and don't want to do more work than necessary. That is to say, mathematicians work smart, not hard.
Arithmetic Series
edit|
Example 2.1.1.a: What is ? This is a classic example among many mathematicians. You may be reaching for your calculator, but that will definitely take a long time to punch in all those numbers, and you may accidently make mistakes while writing out the expression. The question is, how do we solve this in the short amount of time we are given on the CLEP exam? Notice that there is a pattern at play: the first term of the series, , plus the last term of the series, , will give us . The second term of the series, , plus the second-to-last term of the series, , will give us . In fact, for all terms in the series, each pair of numbers, according to their "placement," adds to . Since there are pairs in this series, and the sum of each pair of numbers always yields , |
Let us make a conjecture for the above statement. After all, we are not robots that are simply fed a method and do something the same way. We will contract parts of the above expression in the question above to see if our method will be useful for any number of terms. Let be the number of terms in the arithmetic series , let be the sum of , and let be the column in which the same method we used in Example 2.1.1.a will, hopefully, get us the sum .
Notice how the odd terms have this weird (or perhaps odd) behavior where not all pairs of terms have the same sum (because there is not an even amount of pairs). While it may seem that using the method in Example 2.1.1.a will work for all odd number of terms based on the table above, maybe it is not true for some really high odd term. Therefore, it is important to prove this is true. For now, let us simply define the formula to be true for both even and odd number of terms.
For any finite sequence , where , that contains terms, the sum of each term is
A finite set of things is something that has a determined number of anythng within that set. An infinite set is a set not described by a determined number of the amount within that set.
Note: the above formula is not known as the "Gaussian method" among mathematicians. This wikibooks will simply refer to this method as the "Gaussian method."[see footnote 1.]
|
Example 2.1.1.b: Knowing the sum to an arithmetic series is and the first term is but the last term is , what is the constant difference? This seems like an impossible problem to someone who does not know about the Gaussian method or the properties of an arithmetic sequence. However, since you have paid attention, you can figure out for yourself. For the purposes of giving an example, this Wikibooks will explain. We do not know how many terms there are in the sequence, so let's find out how many terms there are. Since
This subject is not called College Algebra for nothing, so do some algebra.
Note, however, that we are not looking for the number of terms in the series. We want to know the constant difference of the arithmetic series. Therefore, use the arithmetic sequence direct formula: !
|
Example 2.2.1.b helps us know how to find the number of terms and the constant difference. Sometimes, you may simply not know one or both of the information you needed to find in Example 2.2.1.b., more often the number of terms. The next example helps illustrate the usefulness of knowing about the properties of arithmetic series and arithmetic sequences.
|
Example 2.1.1.c: What is the sum of the arithmetic series ? To find the sum, we need to know how many terms there are; otherwise we cannot use the Gaussian method. Because we do not know the sum of the series, let's use the direct arithmetic sequence formula (since we know which terms correspond to place). We want to find the number of terms, , so use the last term (). First, find the constant difference. To get from to , we need to add to . Therefore, the constant difference is . To put it more formally: if recursive formula and , then means . Second, find the number of terms. If , , and , then . Solve for :
Finally, use the Gaussian Method:
|
As you can see, an arithmetic series can be useful in describing any type of sequence. Now that we have sufficiently explored arithmetic series, let's prove that the Gaussian method works for odd number of terms.
Note: what you are about to learn is NOT required for the curriculum. If you do not understand this proof, do not worry, for it does not matter for the CLEP exam. These proofs are only to build a mathematical understanding of the concepts. As such, you may skip these if you want.
Given there are terms in the arithmetic sequence, .
Adding one more term makes the sequence even because is odd: .
Since , adding to the series makes that the last term, so .
Because and , .
will help us find the number of terms we are looking for:
- Since has multiplier for both terms, .
- Because , .
is the same formula we started with; ergo, the same formula works for odd number terms and even number terms.
CLEP Practice Problems: Check Your Understanding
edit
Note, this practice quiz is unfinished.
Proof of Arithmetic Series
editNote: what you are about to learn is NOT required for the curriculum. If you do not understand this proof, do not worry, for it does not matter for the CLEP exam. These proofs are only to build a mathematical understanding of the concepts. As such, you may skip these if you want.
Geometric Series
editWhile it is amazing one can find the sum of an arithmetic sequence, what about the sum of a geometric sequence? Thankfully, mathematicians have found a way to calculate this idea. This theorem (not conjecture, as you will hopefully see with the geometric series proof) is one of many ways mathematicians have found solutions to problems coming from the abstract. As always, it is best to understand the way you can use a formula first before getting the formula introduced. To invoke deeper learning, we want to understand the concept, not reciprocate the formula outloud on a test and say, "I know the answer."
|
Example 2.2.1.a: What is the sum of the geometric series ? Let's define a sum for the geometric sequence:
Notice that all the terms except has a factor . Therefore, move the first term to the other side by subtracting : . Then, factor the two on the left side: The key discovery of this exercise is noticing that is but without , so given that ,
Solve using elementary algebra:
|
Notice how we solved the problem. We said that the sum must equal something positive, so we determined that if it does equal something, we could figure it out in some way without having to do any long calculations. Can we use this method for some general geometric sequence? This how we determine a formula. In your Exploration, you will be tasked with presenting a proof for the formula of the geometric series. We will still give you the formula, but you must prove it yourself in the next exploration. Of course, we will also present another way to prove the geometric series formula in the next section.
Prove: The sum of a geometric series .
We know that will make it so that all terms to the right of the equal sign have factor . Ergo,
Note that , so divide by and apply the identity to the expression to yield
Subtract and write the expression to the left as a fraction:
Multiply by and add :
Factor on the left, factor on the right and divide by :
For any finite geometric sequence , where , that contains terms, the product of each term is
for this Wikibooks[see footnote 2].
Proof of Geometric Series
editNote: what you are about to learn is NOT required for the curriculum. If you do not understand these concepts, do not worry, for it does not matter for the CLEP exam. These proofs are only to build a mathematical understanding of these concepts. As such, you may skip these if you want.
By definition, a geometric series has the sequence , with . As a result, the following is true: .
Let .
Add to both sides:
Subtract to the other side:
Factor the common ratio to all terms in the left side of the equation:
Factor for the expression to the right side of the equation:
Notice that because , we can substitute that into the expression on the left side:
Finally, solve for :
Therefore, the sum of a geometric series must be .
Sigma Notation
editHow many of you are tired of writing out the expressions? How many of you are tired of figuring out how many expressions there are in a series? Where is this short-hand that we conveniently have for an arithmetic or geometric sequence? Thankfully, all of your answers are coming soon.
Say you want to write out the expression , in which there are terms in the series, each of which are the number . We hopefully can evaluate the series without having to think too much about it, or even think about a short-hand about this expression immediately without too much thought. However, the purpose of this easy exercise is to introduce a new notation.
Let denote the sum of a series. Located at the bottom of the symbol is the start of the series at index (blue) and the top of the symbol is the last index of the series, (red). The term inside the parentheses represents the sequence that the series follows, (orange). The use of the notation of is shown below Here, we know that must have the sequence .
Interpreting the meaning of tells us that for any number in the sequence, the th term of the expression is . Knowing that the sequence starts at index , meaning , and there are terms, meaning , we may write the sigma notation as below:
It is important to write the sigma representation having in parenthesis. Often, if you don't have it, you can confuse other terms by accident. It is for this reason that this Wikibooks recommends writing the term in parentheses.
For any series that has formula , starting from arbitrary point , and given terms, the sigma representation is written as follows:
Some more ways in which sigma notation is written is often a short-hand, especially when handwriting. This should be used if you want to save time.
Before we jump into our exploration, it may be a good idea to introduce some more expressions that can be rewritten into its sigma form equivalents. Some of the expressions may not even follow from a formula we have seen so far. Nevertheless, let us continue with this concept.
|
Example 2.3.1.a: Write the sequence into its sigma form equivalent: A good idea before getting started is to look for any possible patterns. Because you are working with sigma notation, check whether there has to be a pattern involving addition. Look at the numerator of the first two terms. Let us assume we are starting at index . To get from the first term in the numerator to the second term in the numerator, one simply has to add 1 to the first term. Similarly, to get from the first term in the denominator to the second term in the denominator, one simply has to add 2 to the first term. Both of these are true on a term-by-term basis.
Because this function is true, let us use this to find the number of terms in the expression (i.e., look at the final term in the expression).
We have demonstrated this expression involves 70 terms. With the index, number of terms, and function ready, we may now write the sigma equivalent: Alternatively, one can change the index to get a completely different sigma notation. Notice how when the index starts at an , the formula and the final term's index also changes. Here, we will look specifically at . Keeping in mind the index represents the placement along the series, going from 2 to 3 is simply a matter of changing along with the numerator. Because the denominator is simply the same idea except displaced by 1 more than the index, the denominator follows a pattern of . Therefore, the function of the sigma notation is
Use this function to find the the final term's index.
Knowing the index starting point, function, and final index, the sigma form of this situation is Notice how the pattern changed. Quite intriguing, would you not say? |
Some expressions are too hard to determine simply from looking. These are likely going to involve factors multiplied to another. THe best way to determine such a pattern would be to divide terms to see what the factors are.
|
Example 2.3.1.b: Write the sequence into its sigma form equivalent: There seems to be no pattern here. The best thing to do is to determine any similarities between terms and see if there seems to be a pattern from there. Notice how the first and fourth term are zero. This means that there is a term that allows us to obtain a value of zero. Let us assume they are linear functions. If is the index of the first term and is the third term, then a possible summation function is . Let us apply this and see if it works. It seems this function works for each term. Therefore, this works. |
More examples will be added later. The next exploration will ask you write out a variety of expressions using sigma form:
(a)
(b)
(c)
(a) Remember how we needed to find out how many terms there are in a sequence and the constant difference to find the sum of an arithmetic sequence? It is the same here. The sigma representation, well, represents the adding of each term in the series. In which case, we need to know the constant difference and the number of terms in the series to determine any validity from it. Note how is an arithmetic sequence that has the common difference two. Therefore, given the first term is , the arithmetic sequence formula is . From this, we can determine the final term's position: . After solving for , you find that there are terms in the sequence. As such, you may finally write out the final answer:
Note, because you can start counting the terms at , you may rewrite the expression as follows:
(b) Use the same idea from item (a) to rewrite the expression into its sigma equivalent. Notice that the series shows a geometric series, with common ratio of starting at . Therefore, . Since there is no need to use a formula to find out how many terms there are in the series, simply count and you have your answer:
Again, you may rewrite the sigma form equivalent starting at :
(c) There are two series shown in the expression. Separate each series within as the following: and . Both and are arithmetic sequences but with different differences and starting numbers. Instead of explaining each one, only the formula will be provided for each sequence: and . Note that the starting number and end numbers are not appropriate to use in the same sigma notation, so separate them into two sigma representations and add them together. Thus, the sigma representation for this expression is
Do you see why we ask you to write the formula using parentheses? Also, you may have separated the series differently. In which case, if and , then and , where has terms and has terms. Therefore, another representation is also appropriate:
(d) There are two series shown in the expression. Separate each series within as the following: and . While is geometric, with common ratio , is arithmetic, with constant difference . Instead of explaining each one, only the formula will be provided for each sequence: and . Because of the difference in formula and difference in starting numbers used, it is impossible to put them together in the same sum. Therefore, the sigma form of the series is
Notice how you added the other term instead of substracting. If you were to subtract the second sigma representation you would in effect flip the sign on every other term. As such, the second series representation would be wrong unless you were to change it to this:
Sigma Simplification Techniques
editIn some textbooks, this section would be called rules. We call them what they really are: techniques to simplify common sigma representations.
For any series that has constant term , starting from index , and given terms,
As always, if you are confused, write out some terms. The above sigma representation states that for any constant term added times, the resulting sum is equivalent to . Never forget that multiplication is repeated addition. This axiom you heard in elementary school is still important to this day.
For any series that has constant term multiplied by changing index , starting from index , and given total terms,
This second "rule" can be simplified as the following. Since , we can conclude that . Each term in the expression has common factor , so . Notice that each term on the inside of the parenthesis is a basic series where starting at goes to final term as a sum, so
For any series that has constant term in addition to changing index , starting from index , and given total terms,
This one is harder to see why it is true. As always, however, try it out by hand. Remember that sigma notations are short hands of sums that have some sort of formula, so write out a term in case you are ever confused. Notice that . Because adding is commutative, and because the parentheses do not change the sum of the series, you may group terms such that We have already determined the sigma notation for each grouping, so we may put it together to say the following is true:
For any series that has constant term in addition to the range of the function of or , starting from index , and given total terms,
Realize that the above "rule" is simply an extension of the previous one. If , then . Realize that any function can comply with this rule. By extension:
Using this general knowledge, one can also argue the next following "rule":
For any series that has constant term multiplied by the function of or , starting from index , when adding constant to the product, and given total terms,
Given the way we found the same identities, you may do the proof for this one by yourself as an exercise in sigma notation. The best way to understand this new notation is to practice it. (Of course, this Wikibooks will provide plenty of practice.)
Along with that practice, you may also try to show that the identity for the next "rule" is also true:
For any series in which the formula is two different arbitrary functions: and , starting from index , and given total terms,
With this, you now have a sufficient foundation for the necessary tools needed to prove and disprove statements as well as create your own identity. Before we move on the next section, we must mention the sigma identity for each of the series type we learned in this wikibooks.
Sigma Identities for Series Types
editWhat is the sigma identity of an arithmetic series? Before we give you the identity, it is important to understand arithmetic series. If the person reading this wikibooks has jumped from one section to the other, we may recommend you read anything from the previous if the current reasoning seems to not make sense. First, how do we write an arithmetic sequence using a formula? Like this:
The formula for how to find an arithmetic series is this:
Notice how is in both formulas, so substitute for and you get:
Because is also a formula that helps us find each term in the series, we have finally created our sigma identity:
An arithmetic series in which the formula is , starting from index , and given total terms,
We can use the same process to find the sum of a geometric series. You may consider this your next exercise proving that the sigma form of the geometric series is the same one shown below.
A geometric series in which the formula is , starting from index , and given total terms,
Check Your Understanding
editThe problems below are basically comprehension questions. If you can do all the problems below, you understand all you need to know about sigma notations. Keep in mind, these problems are much harder than usual CLEP problems; however, being able to do these problems with proficiency proves understanding of the material at a deeper level, which means you are better prepared for easier problems and harder problems down the line.
1. Find the smallest necessary to give the smallest real number for the expression below. After, simplify and calculate for the smallest real value. Do not round your answer, and do not use a calculator or program.
Separate the two expressions inside the sum by applying a property rule, given constant and :
Since , and is arithmetic, it must be that case that
From there, put the sum of the two expressions over the same denominator and simplify:
Finally, note that the zero factor property gives if and only if or or both. However, for a zero factor property in which the two multipliers give a positive product, it must be the case that either and are positive or and are negative. Through that logic, we can determine four possible solutions: and , OR and . Despite the four solutions, only one solution must be true: because sigma notations only work through or being the set of positive integers in the situation described in the problem. As such, all greater than gives an acceptable solution. However, this is only the first part of the problem. Now comes the easy part.
The smallest number must be in the situation described above:
Finally, simplify to get the final answer:
3. A rectangle is drawn on the first quadrant of the plane. A cut-and-paste is an iterative process such that the original rectangle is duplicated and the width of the duplication decreases by units and the height of the duplication increases by unit. This new rectangle is displaced atop the original with its left-most height attached leftmost the original. The duplication is then cut-and-paste. This process continues until the width of the final duplication is at least unit or at most units. The length must be an integer. Given the rectangle, what is the cumulative area of the cut-and-paste figure? Write this in terms of a summation and then write the final answer. Show your work.
Notice the why the above answer is wrong. Multiplying the products of two sums does not imply the product is the sum of each index. It is the product of the sum of all the index with the given functions. The student that realizes this mistake will soon realize this problem is harder than it is.
The problem can be easily fixed if one fixes the parentheses. Recall how we always state to pay attention to parentheses. This is one big reason why. The student that made the mistake above realizes a trick but did not utilize it correctly. As a result, the above answer is an over-estimate of the correctly applied solution.
Let the length of each index be and the width be . Analyzing the pattern for this above process gives us insight into the resulting area of the cumulative area for each index. We want to find the end result, some , that allows the width to be the following:
- .
First, notice how function is arithmetic and decreasing. We start at , and the difference is , so
- .
The same is true for . Because the width starts at and ends at ,
Given we know ,
For , . Therefore, is also a maximum. The cumulative area function is given by:
All that is left to do is apply the formulas and use a calculator to find the answer:
Infinite Geometric Series
editThere is this old and famous paradox that perplexed many who listened to it. The problem stems from the Greek thinker Zeno of Elea. This old adage was the first example of reductio ad absurdum (disproving a statement by showing that the application of the statement will lead to a contradiction, and so the original statement cannot be true). However, today, a version is no longer a paradox, and it took the invention of calculus to prove this enigma is not an enigma[see footnote 3].
The version of the problem that demonstrates the enigma is proven and shown below.
Note: the paradox will be shown soon.
The age-old questions of most students in mathematics arise: "When are we going to need this?" The next exploration gives one problem in which everything you have learned will be tested. This is definitely harder than many CLEP exam questions; however, problems are what make you better at math. You learn as you do, and so you must.
(a)
(b)
- (i) Given general form of expression (b), find at least two integers, and , that will make the general expression equal to a perfect cube number. If it is impossible, prove that it is not possible.
(c)
- (i) Given general form of expression (c), prove there are infinitely many distinct integers and that will make the general expression equal to a perfect square. Give at least one example.
(a)
Since each term must converge to some finite value, and since each term in the sequence is multiplied by the , it is best to think of this problem as if were one term in the sequence. Discover the pattern and you may evaluate each series. Let . Note that
If we keep the pattern going for each term, we find that . This is simply a recursive geometric sequence, so in effect, as we keep adding terms to infinity in the exponent, . Note that is an infinite geometric series, so we may use the summation formula:
- . Therefore, because , the following is also true: . As such,
Note: there is another way to "solve" these type of expressions; however, the method does not "prove" the general convergence towards a number and simply denotes a probable solution(s) to the problem. Using the method above will demonstrate clear convergence rather than the other method.
(b)
The same idea for (a) is used. The only difference will be that the sequence denotes a general pattern for a given term inside a square root. Note that first term and second term . Given , the following must be true: . If we keep the pattern going, we find the following is true: . As you keep going towards infinity, the power has an infinite geometric series that has
- . Note: , the following is also true: . As such,
- (i)
- Let be a perfect cubed number for . If , then for , .
- Given this information,
- Because does not belong to the set of integers, there can be no possible solution for this given problem.
(c)
Again, a similar idea is used as in (a) for solving the expression, although this one may be the most difficult one. Here, the difference is you cannot use simply because is inside the square root. Instead, use . To continue the second sequence, . In fact, the recursive formula continues as such: . Focus on :
Because multiplying is commutative, multiply all terms involving the same base to the other and group it like so:
- .
From here, it is very easy to see that the expression will on the next pattern be . This is simply because the values alternate inside the given square root. As the value of one is alternated, the value of each square root increases by per number. Since a multiple of each number does not care about the order by which it is multiplied (i.e. multiplication is commutative), place the common base multipliers next to the other to get what we found. Therefore, a pattern emerges that can be exploited:
Let tend towards infinity. Evaluate each function to find the final value:
Therefore, the final value for (c) must be
- (i)
- As can be easily be inferred from item (c), . To make the result a positive integer, where , it needs to be the case that and , for .
- Let . Substituting for information we know,
- .
- Let .
- .
- There exists some that allows the expression to be square. Because a value simply needs to be cube for each, there exists infinitely many possibilities. One non-trivial example would be , which will result in the perfect square , for which the square root gives . Taking the square root further gives ; furthering such actions gives .
Proof of Infinite Geometric Series
edit. How do we prove this is true? Again, this is way above most curriculum required textbooks. However, the goal of many mathematics textbooks is to get the user inspired in math and to use those concepts into other fields of interest. No matter what given field a person is going into, they are going to need to solve problems: a history major needs to understand what a person meant; an English major needs to find the right words that help them convey their ideas; a Science major will have to apply mathematical concepts to communicate ideas about science. As such, learn to love problems, for conquering a problem will make you stronger.
Note: what you are about to learn is NOT required for the curriculum. If you do not understand these concepts, do not worry, for it does not matter for the CLEP exam. These proofs are only to build a mathematical understanding of these concepts. As such, you may skip these if you want.
Prerequisite for the proof: Imagine we want to find values of some function . Define this function as . If , then . Well, it seems this value is undefined when , so it seems it does not equal anything. However, let's try graphing this rational function.
First, let us divide: . It seems once we simplify the rational expression, we are left with . However, This is not exactly true because our function is still undefined at , so we must add a constraint: . To put it more formally:
If we graph the relation, we find that there is a "hole" at that point in the function. Let's use values close to 2 so that we abide by those rules.
It becomes clear that as values get "closer and closer" to , "approaches" . What is "close"? How close are your eyes to the screen? We would most likely say, "it is 45 cm. away from the screen." In which case, let's use the distance (i.e. absolute value) to define the word "close": and . (Answer this question: why did we use absolute values?)
Let's define this process using two variables and : If , then those two values are "close" or "approaches of function ," where can be any value you want it to be, as long as it tolerates our definition. We can conclude the following: is "close" when is close, given that . If we think about it, we have sufficiently proven what "close" means. Let us put this definition[see footnote 4] up front:
For any , there exists a .
Now, as mentioned, mathematicians like to "work smarter, not harder," so a mathematician does not want to write out "as approaches , approaches ." Instead, we write out using our fancy notation: . This is called "limit." All this notation says is that "as we limit our values of approaching () , we find that approaches ." Now, you have a sufficient foundation for limits and are ready to begin the proof.
Read the prerequisite to understand this proof.
If we want to know what happens as approaches infinity (), we can write it like this:
Note: .
What happens when ? For , the numerator will have values get closer and closer to infinity as and get larger, and therefore, do not converge to a finite value.
What happens when ? For , the denominator will have values , which will . It is indeterminate, and there are no tricks to find a value that it will converge to. As such, when , the limit is indeterminate.
What happens when ? For , the numerator will have values approach as and get larger. Plus, the denominator will never be , so everything works out. If , given that , then .
Note: . Ergo:
Note that by proving the following fact for the limit, we also "prove" the summation representation[see footnote 5].
Exercise Problems
editFootnotes
edit- The WikiBooks simply refers the formula used as the "Gaussian method" because of a famous mathematical tale. There was this intelligent mathematician named Carl Friedrich Gauss who, in second grade, was asked to find the sum of . The teacher that assigned this problem simply wanted some peace and quiet. However, Gauss was able to come up the answer using the same method in Example 1.3.1.a. Legend says that he did not write the method and did all the calculations in his head; he handed the piece of paper with just the answer. Nevertheless, the teacher had to check to see if he was right. It turns out, he was indeed right. If the reader needs to refer to this formula to other mathematicians, simply call it the "sum of an arithmetic series formula," although it does not have the same ring to it as the previous name.
- It is very common for many textbooks to use the following formula for a geometric series: . Both are technically correct; however, this Wikibooks has decided to use because it is easier to remember that you subtract the first term from the final term at index .
- Although described technically correct, calculus was merely one piece of the puzzle that helped in solving the issue. The version that is described is shown in the example, but the original problem did involve calculus concepts that will not be talked about in this Wikibooks since it does not help us understand infinite geometric series.
- Note the formal definition is technically complete; however, the variables refered to the distances are a little different. Instead of , write it as (read aloud as "delta"). Instead of , write it as (read aloud as "epsilon"). Consequently, the definition given for "close" changes: "For any , there exists a ." Also note that the definition may be written a little different as "for any , there is a such that and ." For the interest of not confusing the reader, we decided to make the definition more simple to understand.
- Note that the limit can be used for any function. Let . Say we want to find . We can do that because as we get closer and closer to , we find that gets closer and closer to . However, we can simplify the process by saying that , given that a function is continuous. Because there are no jumps or asymptotes in as long as , we can state . This is why we can use the limit and say that .
Binomial Theorem
Quick question: what is equivalent to? Well, to find that, we need to multiply two times because an exponent denotes how many times, , you multiply any value , which we represent as . Let and .
- .
If this was part of a multiple choice question, you would perhaps be able to quickly get the answer. However, what if you had to do a modified version of this problem?
- Find .
You can perhaps do this problem after a while, but it might already be too late before you can finish the CLEP College Algebra exam. Even if it is not too late, you may not be able to do the other problems after you are done, or you may get the wrong answer because it is very hard to do the problem like that. Therefore, how do we do the problem? That is when the binomial expansion theorem comes into play. We will state the definition once we understand the foundations of the formula first.
Permutations and Combinatorics
editFactorial Notation
edit|
Example 1.1: How many 26-letter words can you make using the standard English alphabet (A-Z), where you can only use a letter once? Let's start small. Try to imagine a list of all the possible -letter words using the standard alphabet. In that list, you would see all the letters of the alphabet. Now try to imagine a list of all the possible -letter words you can make using the standard alphabet. If you think about it, that is simply . After all, you had letters to choose from, but since you are not allowed to use that letter more than once, you now have letters to choose from. This works the same for any combination of -letter words (AB, AC, AD, , BA, BC, , ZA, ZB, , ZY). If you think about it, the pattern continues. The number gets larger, but it gets larger by multiplying the number from before minus . If you want to make a random word that is letters long, where no letters can be repeated more than once, then |
In Example 2.1, we wanted to find the number of 26-letter words you can make, if you can only use a letter once. It can be a bit tedious to write as your answer. However, mathematicians have found a way to write a short hand for it.
For any multiplication of a whole number where is true, let , where "!" is sounded as factorial. By definition, .
Another way to think of a factorial is the multiplication of the current whole number to the number 1.
To make the above definition more clear, here is a list of a few examples:
In Example 1.1, the answer can be rewritten as this:
We use the factorial notation much more than just for a representation of multiplication in specific situations. The factorial is very useful when listing out possibilities or the number of arrangements. Say that you want to find the number of ways you can arrange 4 students in a group. Call each student either A, B, C, or D, only once. Here are some listings:
- A, B, D, C
- A, B, C, D
- A, C, B, D
- A, C, D, B
- A, D, B, C
- A, D, C, B
As we continue listing each arrangement, we find that the number of ways in which you can arrange the four students is , which is equal to . This makes sense because you cannot have an arrangement in which a student repeats in the list (no cloning allowed!).
Say that you want to find the number of ways you can arrange three students in a group. Call each student either B, C, or D, only once. Here are all of the listings of students.
- B, D, C
- B, C, D
- C, B, D
- C, D, B
- D, B, C
- D, C, B
The number of ways in which you can arrange the three students is , which is equal to .
From the two examples above, it should be clear that factorial notation is very useful because we can show that arrangements are simply just a choice between possibilities, then possiblities, etcetera.
Combination
edit|
Example 1.2: A high school is considering making a committee of 6 teachers because of the growing student population size (before: 500 students; after: 700 students). Out of the total 200 teachers in the school, 15 are eligible for the committee. How many committees can be made when 6 teachers are added. Let us imagine a group of 15 teachers. Each one will be assigned a letter from the English Alphabet, in order from A - O. Instead of adding 6 teachers to the committee, let us add 3 teachers, so that we get "a feel" for the situation. In a committee, we do not care about the order in which we find them at a table because we only care about if they are in the committee. Imagine we see three teachers, A, B, and C.
The list you see above does not tell us that there are different teachers, only that the order is different. However, we do not care about the order; therefore, we must exclude the order from the number of possible committees to make the answer representative of the idea of a committee. The numbers of arrangements in which the same number of teachers, , show is . This is what we "factor out," the order in which we find teachers in committees. One final thing to keep in mind is that since we are selecting from a group of , we are excluding or from being arranged into the committee in the same way we expect them to. Therefore, we must "factor out" the ways of arranging those teachers. From this, we learn that we can arrange |
One difference between Example 1.1 and Example 1.2 is that the order in Example 1.2 did not matter. After all, in whichever way you arrange the committee, you count any arrangement where the same elements are within identical to the other. You cannot do that with an arrangement of letters because AB and BA are not identical. Nevertheless, this example is not independent. There are countless times in which you whatever way you arrange a group of something, the number of possibilities does not increase. Therefore, we need a formula and notation for such a situation.
In an arrangement from which objects are selected from a group of objects, where the order of selection does not matter when counting all possibilities, the number of possible arragements is given by
Such a given arrangement is called a combination.
A representation of is or , read aloud as " choose ."
We are now closer one step closer to understand the binomial theorem. We only need to understand a few more things before we use the formula we learned at the very beginning.
Polynomials and Binomials
editPolynomials and Generalization
editLook at the following polynomials below:
The one that is in common with all three of the polynomials above is that they are all added (remember, the inverse of summation for real number is , so ). This means that we have a series. To really hammer that idea into our skulls, we need to go ahead and generalize a polynomial. Here is a formal definition of a polynomial
A polynomial is an arithmetic series of terms whereby the term of at index is . where is the coefficient of and is the power of . Let be the final index and coefficient of the series. The sum of a general series can represent the sum as
Although the definition may seem complicated, there is no need to worry. Remember that every polynomial must have a degree, in this instance, . For every , the coefficient is . If , then . Since each iteration of has a different coefficient, once , we are finished writing the series. Every polynomial, therefore, has the same pattern.
A polynomial is an arithmetic series in which
However, while this may be an incredible mathematical fact, this does not help us with our original problem. After all, we want to be able to predict a polynomial that results from multiplying another polynomial (since a binomial is also a polynomial). However, the above definition gives us a giant hint to help us solve our first problem. Before we create a formula for that situation, however, we must understand one more concept.
Pascal's Triangle
editFrench mathematician Blaise Pascal, like many mathematicians before his time, wanted to study a pattern of sequences and series. However, unlike most patterns we see in this WikiBook, the pattern is not horizontal, but vertical and diagnol. Instead of one-dimensional patterns, we see a two dimensional pattern. This pattern is of a shape of a triangle, which is shown below.






![{\displaystyle =\left[10+(-5)\right]+20}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5771e648f12800c3d36142360fbe91395d8bee9)










































































![{\displaystyle {\begin{array}{|c|c|}a&b&a-b&a+(-b)\\\hline 1&3&1-3=-2&1+(-3)=-2\\\hline 3&4&3-4=-1&3+(-4)=-1\\\hline 5&5&5-5=0&5+(-5)=0\\\hline 7&6&7-6=1&7+(-6)=1\\\hline \vdots &\vdots &\vdots &\vdots \\\hline 2a+1&b+3&2a+1-(b+3)&2a+\left(-\left[b+3\right]\right)\end{array}}\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8718d738a9eb140a4b44b27aadac6e8f2f326d1e)




































































































































































































































































































































![{\displaystyle {\begin{aligned}\mathbf {F} _{f}&=-gM\mu _{k}\\&=-{\frac {3}{2}}\cdot {\frac {1}{2}}\cdot 10m&{\text{[Clearly false, but let us continue.]}}\\&=-{\frac {3}{2}}\cdot 5m\\&=-{\frac {15}{2}}m\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71c243e81155bb1dc97305fde05049f192384012)



![{\displaystyle {\begin{aligned}A-B&=Ma-[-ma]=(M+m)a\\&=\left(\mathbf {F} _{T}+\mathbf {F} _{f}\right)-\left(\mathbf {F} _{T}+\mathbf {F} _{w}\right)\\&={\color {Red}\mathbf {F} _{T}}+\mathbf {F} _{f}-{\color {Red}\mathbf {F} _{T}}-\mathbf {F} _{w}\\&={\color {Red}\mathbf {F} _{T}}-{\color {Red}\mathbf {F} _{T}}+\mathbf {F} _{f}-\mathbf {F} _{w}\\&={\color {Red}0}+\mathbf {F} _{f}-\mathbf {F} _{w}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae834018fa8b4bbe3b2c61957431b6c6445063b5)











![{\displaystyle {\begin{aligned}{\frac {g\left(-M\mu _{k}+m\right)}{M+m}}&=\left(g\left(-M\mu _{k}+m\right)\right)\left(M+m\right)^{-1}\\&=g\left(-M\mu _{k}+m\right)\left(M+m\right)^{-1}&{\text{[}}g{\text{ is on the very left here.]}}\\&=g{\frac {-M\mu _{k}+m}{M+m}}\\&=g{\frac {m-M\mu _{k}}{M+m}}&\left[-M\mu _{k}+m=m-M\mu _{k}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fe8e985cd306712bd578bb2ad79b5eda63e3087)

























![{\displaystyle {\begin{aligned}2S_{1}&=2\left[2\cdot {\frac {1}{2\cdot \left(x+{\tfrac {4}{3}}\right)}}-{\color {Red}{\frac {y}{2}}}\right]&\left[{\text{Recall }}C{\tfrac {1}{a}}={\tfrac {C}{a}}{\text{.}}\right]\\&=2\left[{\frac {2}{2\cdot \left(x+{\tfrac {4}{3}}\right)}}-{\color {Red}{\frac {y}{2}}}\right]&{\text{[Recall the distributive property.]}}\\&={\color {Green}2}\cdot \left[{\frac {2}{{\color {Green}2}\cdot \left(x+{\tfrac {4}{3}}\right)}}\right]-{\color {Green}2}\left({\frac {\color {Red}y}{\color {Green}2}}\right)&{\text{[Green colors will be eleminated.]}}\\&={\frac {2}{x+{\tfrac {4}{3}}}}-{\color {Red}y}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa107ba622d7c5d3d0c8d406e24018647cd873ae)



![{\displaystyle {\begin{aligned}{\frac {1}{x}}\cdot \left(-2S_{1}\right)&={\frac {1}{x}}\left[-{\frac {2}{x+{\tfrac {4}{3}}}}+{\color {Red}y}\right]\\&={\frac {1}{x}}\cdot \left[-{\frac {2}{x+{\tfrac {4}{3}}}}\right]+{\frac {1}{x}}\cdot {\color {Red}y}\\&=-{\frac {2}{x\left(x+{\tfrac {4}{3}}\right)}}+{\color {Red}{\frac {y}{x}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75933ea020a14cdb0cae801cec468749a8666ff1)































































































































































































































































































































































































































































































































![{\displaystyle xy\left[{\color {Red}x\left(y^{2}+2\right)}+{\color {Green}4\left(y^{2}+2\right)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc7b13d2772f580add69e8e1200424fd0ba23fb4)



![{\displaystyle xy\left[C\left(x+4\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c4c3ebc32473fd6a4f1fa49cb1eb537e832eec5)
![{\displaystyle xy\left[\left(y^{2}+2\right)\left(x+4\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96e128dfe50f18b0ca5556d2f1ccdf4319952546)














































































































































































































































































































































































































































































































































































































































![{\displaystyle x_{k+1}=a+d([k+1]-1)=a+dk}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d424953aef6fa4a333a5357b8862f4ed059746a7)











![{\displaystyle {[2a+d(k-1)]\cdot {k \over 2}=[a+a+d(k-1)]\cdot {k \over 2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dc75a5496c48973d6e34d31048ee2d8a1a4887f)
![{\displaystyle {[a+a+d(k-1)]\cdot {k \over 2}=\left(a+x_{k}\right)\cdot {k \over 2}={a+x_{k} \over 2}\cdot k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d1d64822ce97b82d97df307d4704c13f149ee27)




































































































































![{\displaystyle S_{a}={2a+(k-1)d \over 2}k=ak+{(k-1)d \over 2}k=\left[2a+(k-1)d\right]{k \over 2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ab4d80a1bbdf0078d148f729bad9ced9eff7bcb)














































![{\displaystyle A(k)=\sum _{i=1}^{k}\left[w(i)\cdot l(i)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ae06de3e16e63ff67f7946b6dfb82f0126a443d)
![{\displaystyle {\begin{aligned}A(k)&=\sum _{i=1}^{k}\left[(i)\cdot \left(58-3(i-1)\right)\right]\\&=\sum _{i=1}^{k}\left[58i-3i(i-1)\right]\\&=\sum _{i=1}^{k}\left(58i-3i^{2}-3i\right)\\&=\sum _{i=1}^{k}\left(55i-3i^{2}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a40bf95f08b328622f3883a0694517c0816a014b)


![{\displaystyle 10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{\ldots }}}}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64bd694230787a88d2647ae13cff3d1fe9449f82)
![{\displaystyle a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{\ldots }}}}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a870e92467e2f8f97edede6da4e42a290f3b58a)













![{\displaystyle a_{2}=10{\sqrt[{n}]{10}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8660737303b480c2f2f62110a6699df143851341)
![{\displaystyle {\sqrt[{k}]{a^{m}}}=a^{m \over k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7c7097d25a930225318ced082ac1777c16e1616)





![{\displaystyle 10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{10{\sqrt[{n}]{\ldots }}}}}}}}}}}}=10^{\frac {n}{n-1}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d8e543bb0f2f52edb69fafdbeafbcab833aeda7)


![{\displaystyle a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{\ldots }}}}}}}}}}}}=x=u^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72682d088beb78d9f4bcec1b8612c080dd71432b)
![{\displaystyle a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{a{\sqrt[{n}]{\ldots }}}}}}}}}}}}=a^{\frac {n}{n-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61c2000352ac4ebee2117d3afa33687ba08146fd)






![{\displaystyle x_{2}=3{\sqrt {5{\sqrt {3{\sqrt {5}}}}}}=3\left(5\left[3\left(5\right)^{\frac {1}{2}}\right]^{\frac {1}{2}}\right)^{\frac {1}{2}}=3\cdot 5^{\frac {1}{8}}\cdot 3^{\frac {1}{4}}\cdot 5^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36c0045c49f67a5956f44e57897ae368d27855e6)



![{\displaystyle \left(3^{f(n)}\right)\left(5^{g(n)}\right){\text{, where }}f(n)=\sum _{n=1}^{k}\left({\frac {1}{4}}\right)^{n}{\text{ and }}g(n)=\sum _{n=1}^{k}\left({\frac {1}{2}}\left[{\frac {1}{4}}\right]^{n}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60e853ae122b3e3e3beb11f85ef542739418a204)

![{\displaystyle g(n)=\sum _{n=1}^{\infty }\left({\frac {1}{2}}\left[{\frac {1}{4}}\right]^{n}\right)={\frac {\frac {1}{2}}{\frac {3}{4}}}={\frac {2}{3}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20d072426b59ed0fd9f7ab0c8528a0fb1d50970d)











































































































