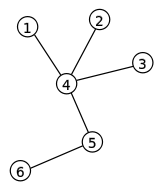
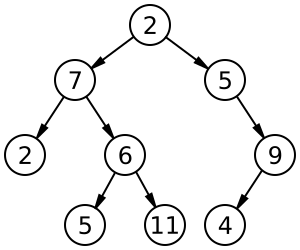
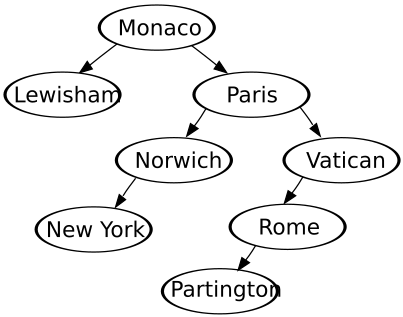
Trees
Connected means that every node is connected to at least one other node. Undirected means there is no direction associated with an edge, i.e. lines are used, not arrows. A cycle is a circuit (a succession of edges that start and end at the same vertex) in which all the edges are different and all the vertices visited are different (apart from the start and end vertex).
A rooted tree is a tree in which one vertex has been designed as the root and every edge is directed away from the root.
|
Exercise: Unordered Binary Trees
|
|
Exercise: Ordered Binary Trees To work out the following you begin at the root of the tree, if the second input is higher than the root it goes to the right of the root, whereas if it is lower than the root it goes to the left. the third input is then used, if it is higher than the root then it gets passed to the right, if there is already a input on this segment of the tree the input is compared with the input that is in there, if it is higher than the input it is passed to the right and if it is lower it is passed to the left, this process continues until all inputs have been dealt with and the tree is complete. Create a binary tree for the following data input: 5, 2, 6, 8, 4, 1, 9, 7, 3 Create a binary tree for the following major city input: Monaco, Paris, Vatican, Rome, Norwich, Lewisham, New York, Partington Create a binary tree for the following list of animals: Elephant, Cat, Dog, Hippo, Giraffe, Lion, Bear Answer:
|