Cg Programming/Unity/Bézier Curves

This tutorial discusses one way to render quadratic Bézier curves and splines in Unity. This is the first of a few tutorials that demonstrate useful functionality of Unity that is not directly associated with shaders; thus, no shader programming is required and all the presented code is in C#.

There are many applications of smooth curves in computer graphics, in particular in animation and modeling. In a 3D game engine, one would usually use a tube-like mesh and deform it with vertex blending as discussed in Section “Nonlinear Deformations” instead of rendering curves; however, rendering curved lines instead of deformed meshes can offer a substantial performance advantage.

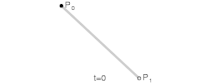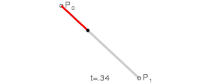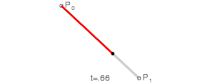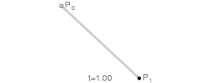
Linear Bézier Curves

The simplest Bézier curve is a linear Bézier curve $B(t)$ for $t$ from 0 to 1 between two points $P_{0}$ and $P_{1}$ , which happens to be the same as linear interpolation between the two points:

$B(t)=(1-t)P_{0}+tP_{1}$

You might be fancy and call $1-t$ and $t$ the Bernstein basis polynomials of degree 1, but it really is just linear interpolation.

Animation of a sampling point on a quadratic Bézier curve with control points P0, P1, and P2.

Quadratic Bézier Curves

A more interesting Bézier curve is a quadratic Bézier curve $B(t)$ for $t$ from 0 to 1 between two points $P_{0}$ and $P_{2}$ but influenced by a third point $P_{1}$ in the middle. The definition is:

$B(t)=(1-t)^{2}P_{0}+2(1-t)tP_{1}+t^{2}P_{2}$

This defines a smooth curve $B(t)$ with $t\in [0,1]$ that starts (for $t=0$ ) from position $P_{0}$ in the direction to $P_{1}$ but then bends to $P_{2}$ (and reaches it for $t=1$ ).

In practice, one usually samples the interval from 0 to 1 at sufficiently many points, e.g. $B(0),B(0.05),B(0.1),B(0.15),B(0.2),...,B(1)$ and then renders straight lines between these sample points.

Curve Script

To implement such a curve in Unity, we can use the Unity component LineRenderer. Apart from setting some parameters, one should set the number of sample points on the curve with the function SetVertexCount. Then the sample points have to be computed and set with the function SetPosition. This is can be implemented this way:

float t;
Vector3 position;
for(int i = 0; i < numberOfPoints; i++)
{
	t = i / (numberOfPoints - 1.0f);
	position = (1.0f - t) * (1.0f - t) * p0 + 2.0f * (1.0f - t) * t * p1 + t * t * p2;
	lineRenderer.SetPosition(i, position);
}

Here we use an index i from 0 to numberOfPoints-1 to count the sample points. From this index i a parameter t from 0 to 1 is computed. The next line computes $B(t)$ , which is then set with the function SetPosition.

The rest of the code just sets up the LineRenderer component and defines public variables that can be used to define the control points and some rendering features of the curve.

using UnityEngine;

[ExecuteInEditMode, RequireComponent(typeof(LineRenderer))]
public class Bezier_Curve : MonoBehaviour 
{
	public GameObject start, middle, end;
	public Color color = Color.white;
	public float width = 0.2f;
	public int numberOfPoints = 20;
	LineRenderer lineRenderer;

	void Start () 
	{
		lineRenderer = GetComponent<LineRenderer>();
		lineRenderer.useWorldSpace = true;
		lineRenderer.material = new Material(Shader.Find("Legacy Shaders/Particles/Additive"));
	}
	
	void Update () 
	{
		if( lineRenderer == null || start == null || middle == null || end == null)
		{
			return; // no points specified
		}

		// update line renderer
		lineRenderer.startColor = color;
		lineRenderer.endColor = color;
   		lineRenderer.startWidth = width;
		lineRenderer.endWidth = width;

  		if (numberOfPoints > 0)
   		{
    			lineRenderer.positionCount = numberOfPoints;
		}

		// set points of quadratic Bezier curve
		Vector3 p0 = start.transform.position;
		Vector3 p1 = middle.transform.position;
		Vector3 p2 = end.transform.position;
		float t;
		Vector3 position;
		for(int i = 0; i < numberOfPoints; i++)
		{
			t = i / (numberOfPoints - 1.0f);
			position = (1.0f - t) * (1.0f - t) * p0 
			+ 2.0f * (1.0f - t) * t * p1 + t * t * p2;
			lineRenderer.SetPosition(i, position);
		}
	}
}

To use this script create a C# Script in the Project Window and name it Bezier_Curve, double-click it, copy & paste the code above, save it, create a new empty game object (in the main menu: GameObject > Create Empty) and attach the script (drag the script from the Project Window over the empty game object in the Hierarchy Window).

Then create three more empty game objects (or any other game objects) with different(!) positions that will serve as control points. Select the game object with the script and drag the other game objects into the slots Start, Middle, and End in the Inspector. This should render a curve from the game object specified as “Start” to the game object specified as “End” bending towards “Middle”.

A quadratic Bézier spline out of 8 quadratic Bézier curves.

Quadratic Bézier Splines

A quadratic Bézier Spline is just a continuous, smooth curve that consist of segments that are quadratic Bézier curves. If the control points of the curves were chosen arbitrarily, the spline would neither be continuous nor smooth; thus, the control points have to be chosen in particular ways.

One common way is to use a certain set of user-specified control points (green circles in the figure) as the $P_{1}$ control points of the segments and to choose the center positions between two adjacent user-specified control points as the $P_{0}$ and $P_{2}$ control points (black rectangles in the figure). This actually guarantees that the spline is smooth (also in the mathematical sense that the tangent vector is continuous).

Spline Script

The following script implements this idea. For the j-th segment, it computes $P_{0}$ as the average of the j-th and (j+1)-th user-specified control points, $P_{1}$ is set to the (j+1)-th user-specified control point, and $P_{2}$ is the average of the (j+1)-th and (j+2)-th user-specified control points:

      p0 = 0.5f * (controlPoints[j].transform.position 
         + controlPoints[j + 1].transform.position);
      p1 = controlPoints[j + 1].transform.position;
      p2 = 0.5f * (controlPoints[j + 1].transform.position 
         + controlPoints[j + 2].transform.position);

Each individual segment is then just computed as a quadratic Bézier curve. The only adjustment is that all but the last segment should not reach $P_{2}$ . If they did, the first sample position of the next segment would be at the same position which would be visible in the rendering. The complete script is:

using System.Collections.Generic;
using UnityEngine;

[ExecuteInEditMode, RequireComponent(typeof(LineRenderer))]
public class Bezier_Spline : MonoBehaviour 
{
	public List<GameObject> controlPoints = new List<GameObject>();
	public Color color = Color.white;
	public float width = 0.2f;
	public int numberOfPoints = 20;
	LineRenderer lineRenderer;

	void Start () 
	{
		lineRenderer = GetComponent<LineRenderer>();
		lineRenderer.useWorldSpace = true;
		lineRenderer.material = new Material(Shader.Find("Legacy Shaders/Particles/Additive"));
	}
	
	
	void Update () 
	{
		if (null == lineRenderer || controlPoints == null || controlPoints.Count < 3)
    		{
       			return; // not enough points specified
   		}
		// update line renderer
		lineRenderer.startColor = color;
		lineRenderer.endColor = color;
   		lineRenderer.startWidth = width;
		lineRenderer.endWidth = width;

		if(numberOfPoints < 2)
		{
			numberOfPoints = 2;
		} 
		lineRenderer.positionCount = numberOfPoints * (controlPoints.Count - 2);

		Vector3 p0, p1 ,p2;
		for(int j = 0; j < controlPoints.Count - 2; j++)
		{
			// check control points
			if (controlPoints[j] == null || controlPoints[j + 1] == null 
			|| controlPoints[j + 2] == null)
			{
				return;  
			}
			// determine control points of segment
			p0 = 0.5f * (controlPoints[j].transform.position 
			+ controlPoints[j + 1].transform.position);
			p1 = controlPoints[j + 1].transform.position;
			p2 = 0.5f * (controlPoints[j + 1].transform.position 
			+ controlPoints[j + 2].transform.position);
			
			// set points of quadratic Bezier curve
			Vector3 position;
			float t;
			float pointStep = 1.0f / numberOfPoints;
			if (j == controlPoints.Count - 3)
			{
				pointStep = 1.0f / (numberOfPoints - 1.0f);
				// last point of last segment should reach p2
			}  
			for(int i = 0; i < numberOfPoints; i++) 
			{
				t = i * pointStep;
				position = (1.0f - t) * (1.0f - t) * p0 
				+ 2.0f * (1.0f - t) * t * p1 + t * t * p2;
				lineRenderer.SetPosition(i + j * numberOfPoints, position);
			}
		}
	}
}

The script has to be named Bezier_Spline and works in the same way as the script for Bézier curves except that the user can specify an arbitrary number of control points. For closed splines, the last two user-specified control points should be the same as the first two control points. For open splines that actually reach the end points, the first and last control point should be specified twice.

Summary

In this tutorial, we have looked at:

the definition of linear and quadratic Bézier curves and quadratic Bézier splines
implementations of quadratic Bézier curves and quadratic Bézier splines with Unity's LineRenderer component.