Linear Algebra/Projection

      ← Changing Map Representations Projection Orthogonal Projection Onto a Line →

      This section is optional; only the last two sections of Chapter Five require this material.

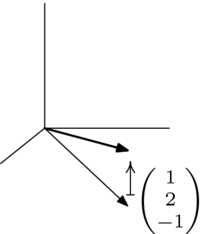
      We have described the projection \pi from \mathbb{R}^3 into its xy plane subspace as a "shadow map". This shows why, but it also shows that some shadows fall upward.

      Linalg projection 1.png Linalg projection 2.png

      So perhaps a better description is: the projection of \vec{v} is the \vec{p} in the plane with the property that someone standing on \vec{p} and looking straight up or down sees \vec{v}. In this section we will generalize this to other projections, both orthogonal (i.e., "straight up and down") and nonorthogonal.

      ← Changing Map Representations Projection Orthogonal Projection Onto a Line →
      Last modified on 25 May 2010, at 18:43