Engineering Acoustics/Sound Absorbing Structures and Materials
Introduction edit
Noise can be defined as unwanted sound. There are many cases and applications that reducing noise level is of great importance. Loss of hearing is only one of the effects of continuous exposure to excessive noise levels. Noise can interfere with sleep and speech, and cause discomfort and other non-auditory effects. Moreover, high level noise and vibration lead to structural failures as well as reduction in life span in many industrial equipments. As an example in control valves, the vibration caused by flow instability occasionally defects the feedback to the control system and resulting in extreme oscillations. The importance of noise issue could be well understood by looking at regulations that have been passed by governments to restrict noise production in society. Industrial machinery, air/surface transportation and construction activities are assumed to be main contributors in noise production or so called "noise pollution".
Noise Control Mechanisms edit
- Active Noise control
Modifying and canceling sound field by electro-acoustical approaches is called active noise control. There are two methods for active control. First by utilizing the actuators as an acoustic source to produce completely out of phase signals to eliminate the disturbances. second method is to use flexible and vibro-elastic materials to radiate a sound field interfering with the disturbances and minimize the overall intensity. The latter method is called active structural acoustic control (ASAC).
- Passive Noise Control
Passive noise control refers to those methods that aim to suppress the sound by modifying the environment close to the source. Since no input power is required in such methods, Passive noise control is often cheaper than active control, however the performance is limited to mid and high frequencies. active control works well for low frequencies hence, the combination of two methods may be utilized for broadband noise reduction.

Sound Absorption edit
Sound waves striking an arbitrary surface are either reflected, transmitted or absorbed; the amount of energy going into reflection, transmission or absorption depends on acoustic properties of the surface. The reflected sound may be almost completely redirected by large flat surfaces or scattered by a diffused surface. When a considerable amount of the reflected sound is spatially and temporally scattered, this status is called a diffuse reflection, and the surface involved is often termed a diffuser. The absorbed sound may either be transmitted or dissipated. A simple schematic of surface-wave interactions is shown in figure 2.

Sound energy is dissipated by simultaneous actions of viscous and thermal mechanisms. Sound absorbers are used to dissipate sound energy and to minimize its reflection.[1] The absorption coefficient is a common quantity used for measuring the sound absorption of a material and is known to be the function of the frequency of the incident wave. It is defined as the ratio of energy absorbed by a material to the energy incident upon its surface.
Sound Absorbing Coefficient edit
The absorbing coefficient can be mathematically presented as follows:
where α, , and are the sound absorption coefficient, one-sided intensity of the reflected sound and the one-sided intensity of the incident sound, respectively.
from the above equation, it can be observed that the absorption coefficient of materials varies from 0 to 1. there are several standard methods to measure sound absorption coefficient. In one of the common approaches,a plane wave impedance tube that is equipped with two microphones is utilized.The experimental setup and dimensions are according to ASTM E1050/ISO 10534-2.[2](Figure 3)The method is done by evaluating the transfer function, between two microphones spaced s apart, and a distance l from sample to get absorption coefficient using the following equations:
Where, are complex pressure amplitude measured by Mic. 1 and Mic. 2 respectively. k is the wave number, s is the microphones spacing and is the absorption coefficent.
According to the standard technique,[2] frequency is limited by microphone spacing as well as tube diameter. It is also recommended that to guarantee the plane wave propagation. The coefficient of commercial absorbing materials is specified in terms of a noise reduction coefficient (NRC) which refers to the average of absorption coefficients at 250 Hz, 500 Hz, 1,000 Hz, and 2,000 Hz. Average values of some acoustic insulating materials that are used in buildings are tabulated in table 1. Based on their construction and material structure, sound absorbers are categorized as non-porous and porous absorbers.

| Material | Sound absorption coefficient |
|---|---|
| 6 mm cork sheet | 0.1-0.2 |
| 6 mm porous rubber sheet | 0.1-0.2 |
| 12 mm fiberboard on battens | 0.3-0.4 |
| 50 mm slag wool or glass silk | 0.8-0.9 |
| Hardwood | 0.3 |
| 100 mm mineral wool | 0.65 |
Non-Porous Absorbers ( Absorbing Resonators ) edit
There are Two types of non-porous absorbers that are common in industrial applications. Panel (membrane) resonators and Helmholtz resonators. Panel absorbers are light, thin and non-porous sheets or membranes that are tuned to absorb sound waves over a specific frequency range. The structural resistance of the panel to fast shaping leads to sound absorption. Panel absorbers are defined by their geometry and structural vibration properties. Helmholtz Resonators or cavity absorbers are perforated structures containing very small pores; one example is the acoustic liners that are used inside the aircraft engine frame to suppress the noise emission from the compression and combustion stages. Similar structures are applied in fans and ventilators used in ventilation and air-conditioning systems. The size of the opening, the length of the neck, and the volume of the cavity govern the resonant frequency of the resonator and hence the absorption performance.
Porous Absorbers edit
Porous sound absorbers correspond to materials where sound propagation takes place in a network of interconnected pores such that viscous and thermal interaction cause acoustic energy to be dissipated and converted to heat. Absorptive treatment such as mineral wool, glass fiber or high-porosity foams reduces reflection sound. Porous absorbers are in fact thermal materials and usually not effective sound barriers. The need for significant thickness compared to operating sound wavelength makes porous absorbers dramatically inefficient and impractical at low frequencies.
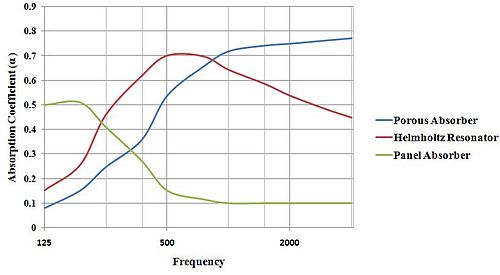
Physical Characteristic Properties of Porous Absorbers edit
The propagation of sound in a porous material is a phenomenon that governed by physical characteristics of a porous medium, namely porosity () , tortuosity (q), flow resistivity (), viscous characteristic length () and thermal characteristic length().
- Porosity
Defined as the ratio of interconnected void volume (air volume in open pores) and the total volume. Most commercial absorbers have high porosity (greater than 0.95). The higher porosity the easier interaction between solid-fluid phases which leads to more sound attenuation.
= volume of the void space.
= total volume of the porous material.
- Tortuosity [1]
the physical characteristics corresponds to the “non-straightness” of the pore network inside the porous material. It shows how well the porous material prevents direct flow through the porous medium. The more complex the path, the more time a wave is in contact with the absorbent and hence the more energy dissipation and more absorbing capability. If the Porous absorber is not conductive, one method to measure it is to saturate the absorbent with an electrically conducting fluid and measure the electrical resistivity of the saturated sample, , and compare to the resistivity of the fluid itself, then the tortuosity can be expressed as follows:
- Flow resistivity
The pressure drop required to drive a unit flow through the material can be related to the viscous losses of the propagating sound waves inside the porous absorber and denoted as flow resistivity . For a wide range of porous materials, the flow resistivity is the major factor for sound absorption. The unit of flow resistance is or and defined as the ratio of static pressure drop to a volume flow (U) for a small sample thickness (d).
- Characteristic lengths [4]
Two more important microstructural properties are the characteristic viscous length and characteristic thermal length ’ that contribute viscous and thermal dissipation. The former is related to smaller pores and the latter is related to the larger pores of porous aggregate. The thermal length is the twice ratio of volume to surface area in connected pores. This is geometric and can be measured directly. The viscous length, , is nearly the same, but each integral is weighted by the square of the fluid velocity v inside the pores and hence, cannot be measured directly.
Acoustic modeling of Porous Absorbents edit
Wave equation in rigid porous absorbents edit
the plane wave equation derived from the linearized equations of conservation of mass and momentum should be modified to account for the effects of porosity, tortuosity and flow resistance. The modified wave equation[5] that governs the sound propagation in compressible-gas filled in rigid porous materials is given by:
where, p = sound pressure within the pores of material
= density of compressible gas
= effective bulk modulus of the gas
q = tortuosity
= porosity
= flow resistivity
The acoustical behavior of a absorptive porous layer can also be investigated from its basic acoustic quantities: the complex wave number and characteristic impedance. These quantities are obtained as a part of solution of the modified plane wave equation and can be used to determine the absorption coefficient and surface impedance. The most practical and common values for the complex wave number and the surface impedance are based on semi-empirical methods and correlated using the regression analysis. One important correlation is suggested by Delany and Bazely [6]
Where, f = frequency σ = flow resistance
Effective Density edit
By assuming rigid-frame pore network in the absorbent, the solid phase would be completely motionless and the frame bulk modulus is considerably greater than that of compressible gas, hence it can be modeled as an effective fluid using the wave equation for a fluid with complex effective fluid density and complex effective bulk modulus. In this situation the dynamic density accounts for the viscous losses and the dynamic bulk modulus for the thermal losses. The effective density relation as a function of dynamic tortuosity was proposed by Johnson et al. [4]
where,
μ = gas viscosity
ω = 2πf
Effective Bulk Module edit
Another factor that affects the sound propagation in the absorbent is the thermal interaction in material due to the heat exchange between the acoustic wave front traveling in the compressible fluid and the solid phase. Champoux and Allard [7]., have introduced a function to evaluate effective bulk module for the gas. as it is observed in the following formula this would be the function of thermal characteristic length ( ).
where,
γ = gas specific heat ratio (for air ~ 1.4)
Pr = fluid Prantdl number
References edit
- ↑ a b Cox, T. J. and P. D'antonio, Acoustic Absorbers and Diffusers, SponPress,(2004)
- ↑ a b ASTM E1050 - 08 Standard Test Method for Impedance and Absorption of Acoustical Materials Using A Tube, Two Microphones and A Digital Frequency Analysis System
- ↑ Link common absorbing materials, absorbing coefficients.
- ↑ a b Johnson, D.L., Koplik, J., and Dashen, R.,"Theory of dynamic permeability and tortuosity in fluid-saturated porous media," Journal of Fluid Mechanics, vol. 176, 1987, pp. 379-402
- ↑ Fahy, F., Foundations of Engineering Acoustics, Academic Press London, (2001).
- ↑ Delany, M.E., and Bazley, E.N., "Acoustical properties of fibrous absorbent materials" Applied Acoustics, vol. 3, 1970, pp. 105-116.
- ↑ Champoux, Y., and Allard, J.F., "Dynamic tortuosity and bulk modulus in air saturated porous media," Journal of Applied Physics, vol. 70, no. 4, 1991, pp. 1975-1979.


























