Clock and Data Recovery/Structures and types of CDRs/The jitter tolerance function

Three magnitude functions of jitter tolerance for the three main loop models in the case of phase-aligner architectures.
For all architectures the lateral eye opening is the same and the length of the elastic buffer (=phase adder) is the same.
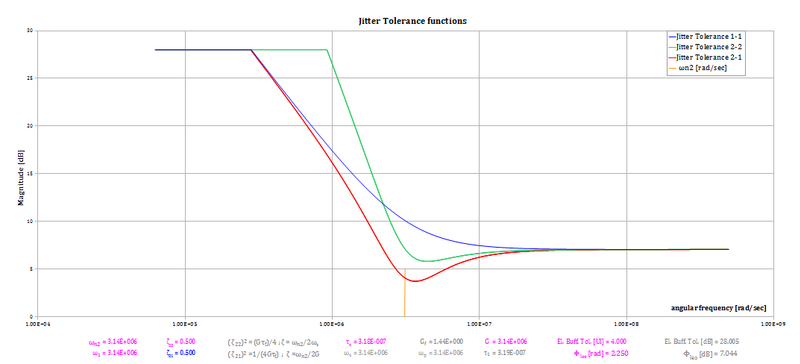
The two important 2nd order PLLs are plotted in the under-damped but significant condition of ζ = 0.5.
The natural frequency is 500 KHz (ω_n= 3.14 e6 rad/sec) and is the same for each of the three loops (yellow marker).

The jitter tolerance of an equipment

In digital networks it is established practice (see for instance some of the ITU-T Recommendations G7xx [1]) to specify, and to characterise by measurement, the jitter that can be tolerated at the input ports of an equipment.

At any frequency of interest, a sinusoidal input jitter is added to the phase of an otherwise flawless incoming signal, and the jitter amplitude is increased as much as the equipment can tolerate. Beyond that limit, the received data stream is not regenerated perfectly and error bits and possibly also slips begin to appear. The same procedure is repeated at different jitter frequencies, to cover all the frequency band of interest for the jitter tolerance and the results are interpolated to obtain a continuous curve.

The boundary of the area (in the plane of jitter frequencies and magnitudes) where the CDR operates without bit errors is then called the curve of jitter tolerance of that equipment.

Note: jitter tolerance curve = measured  ; jitter tolerance function = obtained from models or simulations.

The errors can either be generated by sampling the received pulses too far from the optimum point, or by slips. In both cases, the tolerance limit has been exceeded.

• Slips can either come from exceeding the range of the phase comparator, or by exceeding the range of an elastic buffer. The slip is a catastrophic event in terms of BER because, after its occurrence, 50% (statistically) of the regenerated bits are seen as errors and 50% (statistically) are seen as fictitiously correct. The BER is as high as it can ever be (until the framing circuits are able to get in sync again).
• Error-ed bits. The CDR under test extracts the clock directly from the pulses of the received signal, and then uses it to regenerate the pulses received. The tolerance limit will be reached when the clock that samples the incoming pulses is too far (too early or too late) from the optimum point (the point of “maximum eye opening”, that approximately coincides with the central point between transitions). Such distance from the central sampling point, beyond which errors begin to occur, is called lateral eye opening Φ_LEO. Error-ed bits will give evidence that the tolerance limit has been exceeded (even if they only pop up sparsely in small bursts, at the moments of peak amplitude of the periodic phase error induced by the jitter sinusoidal oscillation).

Remarks

1. The jitter tolerance curve always has a "low-pass" shape. The tracking ability of an equipment is best at low frequencies and is low at high frequencies.
2. At high frequencies, where no more tracking takes place, the equipment can only tolerate the jitter that does not bring the sampling instant to the eye corners. With zero jitter, the sampling point is offset from the central point by the steady state error, if the steady state error is non zero. If the steady state error is zero, the sampling point is in the eye center.
   The tolerance at high frequencies is just a horizontal asymptote, and the asymptote value indicates, for the equipment port under measurement, the difference:Φ_LEO - steady state error

   where the steady state error is the possible error corresponding to an offset of the frequency of the incoming pulses from the free-running frequency of the local oscillator.

   Such error is ${\tfrac {\omega _{p}-\omega _{fr}}{G}}$ [rad] in a slave system of type 1, and is 0 [rad] in a phase aligner system or in any type 2 system.

3. Towards lower frequencies the measured tolerance curve also is asymptotic, but the slope of the asymptote depends on the PLL architecture:
   1. 0 dB/decade, i.e. horizontal, This indicated that an elastic buffer is present to absorb some large low frequency jitter. The horizontal asymptote indicates that the jitter compensation is finite. (The length of the buffer is approximately twice the magnitude of the tolerance represented by the horizontal asymptote).
   2. - 20 dB/decade. This indicated that the receiver is a slave (the local oscillator can follow an infinite phase accumulation, as long as its frequency can track the incoming pulse frequency). The - 20 dB/decade slope tells that the PLL is a type 1 loop (or a type 2 loop whose tolerance is "slew-rate" limited).
   3. - 40 dB/decade. This indicated that the receiver is a slave (the local oscillator can follow an infinite phase accumulation, as long as its frequency can track the incoming pulse frequency). The - 40 dB/decade slope tells that the PLL is a type 2 loop.
4. The tolerance curve sometimes looks like the slope of terraced rice field, with more than one flat section after the first left slope. This indicates that more than one CDR is present along the regeneration path between the injection of the test signal, and that some of them operate at different bit rates.
5. In general:
   1. a flat section, or a flat asymptote, indicates that the tolerance is exceeded in a elastic buffer. Note that the lateral eye opening at high frequencies acts as a elastic buffer;
   2. a section with a slope of -20 dB/decade indicates that (in the related frequency range) the tolerance is exceeded in a PLL operating there like a 1-1 architecture;
   3. a section with a slope of - 40 dB/decade indicates that (in the related frequency range) the tolerance is exceeded in a PLL operating there like a 2-2 architecture.

The tolerance function, a simulation of the tolerance curve

In a feedback loop, like in a PLL for CDR use, the operation is linear, and the linear modeling remains valid, as long as all blocks in the loop operate within their linearity range.

Increasing the input signal amplitude, a point will be reached where one block reaches the limit of its range of linear operation.

Increasing further the input signal amplitude, the linear model loses its adherence to the real system and the actual operation deviates from the modeled behavior.

When investigating the effects of the timing variation of the input signal (the input jitter), the tolerance function (that can be derived using the border between linear operation and the most important hard non-linearities - see below) is of particular interest. It corresponds to the important characteristic of the CDR that is often a precise requirement, specified and measured as a function of the magnitude of the input sinusoidal jitter at different frequencies. The mathematical function can be very close to the measured curve, and is therefore a fundamental engineering tool.

Reaching with the signal level the onset on hard non-linearity inside an internal block often corresponds to the appearance of errored bits in the regenerated data stream. The input signal has then exceeded the level of the CDR tolerance (such level is a function of the frequency of the input signal).

A mathematical derivation of such jitter tolerance function can be made finding out:

1. the block in the loop that is first to reach its limit of non-linear operation and to generate errored bits or slips;
2. the amplitude of the (phase) signal inside such block that reaches the limit of linear operation (such amplitude is a function of ω)
3. the input signal amplitude (function of ω) that generates such internal signal amplitude.

In mathematical terms, defining as W(jω) the signal at a generic node of the CDR model, and as ± Φ_tol the deviation tolerated at that node,

the tolerance function is the locus, for every angular frequency ω, of the magnitude of the input signal X(jω) that produces a W(jω) that reaches, at one or both of its sinusoidal peaks, the tolerance level for that node:

Jitter tolerance = |X(jω)|_{|W(jω)| = Φtol}

is exactly the input (to the CDR) needed for the internal signal to touch the tolerance limit at least at its positive or negative sinusoidal peaks.

Different circuit shortcomings may identify different tolerance functions. These are then combined into one considering, at every frequency, the lowest value among their values.

The function so obtained is called the jitter tolerance function.

In order to derive a tolerance function that simulates well the tolerance curve obtained by measurement, there are 3 (three) fundamental shortcomings of the linear model must be considered :

• the pulse regeneration (= the eye corners and the steady state sampling offset)
• the limited frequency range of the VCO
• the limited range of the (possible) elastic buffer.

The limited range of the phase comparator

The border of normal operation of a phase comparator is reached when the distance in phase between its two inputs exceeds a certain value.

It does not depend on the absolute value of either input, but on their difference only.

The phase comparator is built so that its range covers without discontinuity the period T of one line pulse, and the PLL is designed so that zero difference between the comparator inputs corresponds to the perfect lock of the loop:

Φ_max = -T/2 , +T/2 ⇒ = -π , + π .

When Φ_max is exceeded by the error signal x(t)-y(t), the phase comparator output falls into the next period of its characteristic and its output indicates to the PLL that the closest locking point is now the center of the nearby pulse.

If the transient is short enough the loop has no time to react, the error signal comes back quickly within range, and the output goes back to the original segment of the comparator characteristic. A large burst of errors have affected the CDR, but at the end there is no slip of the recovered clock

If instead the transient lasts long enough for the loop to react, then lock will be achieved at the center of the new segment of the comparator characteristic: a slip has occurred.

Mathematically such limit of linearity of the phase comparator characteristic defines one of the tolerance curves of the closed loop. Such tolerance can be modeled as the locus -for every frequency- of the magnitudes of sinusoidal input signals X(jω) such that :

|X(jω) - Y(jω)| = |Ε(jω)| = $\Phi$_max = $\pi$

But, in the particular case of the measurement of the tolerance curve, as well as in the derivation of the tolerance function, the range extremes of the phase comparator are never reached!

Its range may be exceeded during real operation, in particular during the early phase of a difficult acquisition of phase lock, but it will not be reached while finding the tolerance limit.

In fact, the range of error-less sampling corresponds a sub-range of the phase comparator range. Sampling errors do appear as a consequence of sinusoidal jitter when the lateral eye margin is reached, while the comparator range limit is always larger. The following figure helps identify the quantities involved and clarify the related concepts, and the following sub-paragraph addresses the loop tolerance associated with the sampling phase margin.

The pulse regeneration (= the eye corners and the steady state sampling offset)

The pulse regeneration may not take place at the best instant because of a timing deviation.
There is margin against a bit error resulting from a misplaced sampling instant.
Looking at the eye diagram it is easy to identify the margin.

The tolerance function due to the lateral closure of the eye diagram can be modeled by an equation like the one resulting from the comparator range, but using a tighter range limit, and taking also into consideration the possible sampling offset that exists in some cases.

The input jitter that is not tracked by the PLL leaves a residual (sinusoidal) error between input (that represents the eye center) and output (that represents the sampling instant).

Overall, the output y(t) is not able to track exactly the input x(t) because of two shortcomings:

1. a d.c. offset (the steady state error) and
2. its (sinusoidal) phase variation is not able to replicate exactly the input (sinusoidal) phase variation, and a (sinusoidal) error of the same frequency remains.

When the sinusoidal error adds to the steady state error the sampling may take place before the beginning transition or after the end transition of the pulse.

Just one, or a few, or a high density of errors are equally relevant in the identification of the tolerance limit. In other words, the limit is meant to have been reached when the sampling takes place in what could be a wrong instant, even if the irregular jitter of the beginning or of the end of the pulse do not necessary imply an error at every bit time, but with a lower frequency of occurrence. (It should be remarked that the "irregular jitter" of the transitions happens at random -due to line noise and I.I.- but to a large extent faster than the sinusoidal jitter of the tolerance measurement or simulation).

|X(jω)|_{|X(jω)-Y(jω)| = Φleo}= |X(jω)|_{|Ε(jω)| = Φleo}

where Φ_leo ≤ Φ_max.

When the error signal instantaneously exceeds Φ_leo, error bits are generated in the CDR with a certain probability.

When the error signal exceeds Φ_max and a slip consolidates, the BER remains very high as long as the framing circuits downstream of the CDR re-align (in a real transmission network) or as long as the sequence recognition circuits of the BER tester re-align (in a tolerance curve test set-up) .

The curves in the figure above can be seen as examples, with the exclusion of the flat asymptote towards low frequencies.
The tolerance due to the lateral eye closure decreases with increasing frequency and flattens out at high frequencies.
The clamping of the curves at low frequencies if present because the circuits described incorporate an elastic buffer (see section here below).

The limited frequency range of the VCO and the CDR slew-rate

There always exists the possibility that the PLL is not able to follow a rapidly changing phase of its input because the rate of change of the VCO phase (i.e. the VCO instant frequency deviation) is limited.

This may happen either:

• because the PLL, still operating within its linear boundaries, is simply limited by the loop intrinsic low-pass behaviour. In this case to a sinusoidal input jitter corresponds a sinusoidal phase error signal as well as a sinusoidal output jitter.
• or because the PLL non-linear boundary is reached in the characteristic of the VCO, or of a block preceding it in the loop forward chain.
  The phase error signal is not a sinusoid like the input phase signal. The output phase signal deviates from the sinusoidal input phase with tracts of lower, often constant, slope.
  In this latter case the PLL is " slew-rate" limited. This can occur both because of the VCO characteristics (the VCO gain falls rapidly at the ends of its useful range) or because of the limited range of its drive signal.

The PLL can track the input phase variations, but it cannot react faster than reaching to the frequency extremes of the VCO useful range (the frequency jump is a linear ramp of the PLL phase: the maximum ramp slope of a circuit is called the slew-rate ), and staying there as long as it detects its lag.

Slewing can be defined as a contiguous sequence of ten or more identical phase-error indications.

When the phase of the input signal varies more rapidly than the VCO slew-rate, the phase error that appears may grow for a period long enough to possibly affect the CDR tolerance.

The VCO centering error shall also be kept into consideration: it appears at the VCO input as a voltage shift from the free-running value: V_drive(f_p) - V_drive(f_fr).

Sinusoidal input and slew-rate

Run-length is length of stretches (runs) of repeated bits during which the signal does not change.

The slew-rate limit can be investigated using a sinusoidal input phase jitter, that is the same input signal used for the tolerance curve of the CDR.

The tolerance is measured with a sinusoidal input jitter whose frequency sweeps the frequency range of interest and whose amplitude at each frequency is increased until errors appear.

A sinusoidal function (phase function of time in the case of jitter) has its maximum rate of variation at the zero crossings, that is the tangent at the points of zero crossing.

The slope at the zero crossing is the same of its tangent Aωt, i.e. Aω.

Time diagram of a sinusoid of angular frequency ω and amplitude A,
with emphasis on the maximum slope equal to Aω, that relates to the slew-rate concept

Maximum phase slew-rate = maximum frequency deviation.

The frequency (= the phase rate of variation) that the VCO can generate in response to a step Δ_drive (positive or negative) of its drive signal depends on:

• the amplitude of the drive signal
• the frequency of the VCO immediately before
• whether the VCO reaches one of its range extremes.

It also depends on the relative frequency of input transitions D_T, because the CDR behaves as if the PD gain G_φ was reduced (i.e. multiplied) by D_T.

The open loop gain is defined as G = G_φ G_f G_VCO.

Slew-rate asymptotes with - 20 dB/dec slope and G_VCOV_D intersection

When the VCO is driven away from f_fr, its excursions are limited (up or down) by the limited range of the circuitry that drives it (more than by its intrinsic characteristic, that is very imprecise and variable at the range ends: it is preferable to clamp the VCO range externally).

When driven by a voltage sinusoid V_dsin(ωt), the VCO produces a perfect sinusoid of frequency V_dG_VCOsin(ωt) (and therefore also of phase -(1/ω)V_dG_VCOcosin(ωt) ) with exactly the same 1/2πω period. (The amplitudes of the frequency sinusoid and of phase sinusoid differ by a G_VCO/ω coefficient).

The range for V_d is inevitably finite: let’s call V_D whichever of the two limitations (positive or negative) comes first (i.e. is smallest).

When V_d reaches V_D, the sinusoid encounters a clamp at either or at both of its peaks.

If the input signal of the CDR increases, and tries to drive the amplitude of the signal at the filter output beyond V_D, the VCO output frequency gets correspondingly clamped and the VCO output phase does not fully follow and starts slewing.

The onset of slewing happens when V_d = V_D, that is when the output phase amplitude reaches V_DG_VCO/ω .

In general, there is no slewing as long as :

ω ≤ V_DG_VCO / A_j

Otherwise said, as long as amplitude of the phase jitter at the CDR input A_j ≤ V_DG_VCO / ω , the tolerance is not reduced by the slew rate; when A_j ≥ V_DG_VCO / ω , the phase error due to slewing appears and the tolerance is reduced and its limit may be reached.

Unfortunately the phase error due to slewing is a non-linear function of both A_j (or of V_d) and of ω , and it is not possible to compute it with a closed formula, but only with simulations case by case.

It is convenient to restrict the attention to the onset of slewing because:

• it is a prudent (=conservative) estimation of the tolerance function;
• all CDRs are designed so that slewing never appears for any expected condition of input jitter and run-length.

In a Bode plot the function V_DG_VCO/ω is a line going down with a slope equal to - 20 dB/dec and that intersects the 0 dB ( i.e. magnitude = 1 ) horizontal axis in:

V_DG_VCO/ω = 1 ω = V_DG_VCO

The margin between the onset of slewing and the actual border of the tolerance region (that is defined as the condition where the phase error increases up to the LEO value), is never large, islower at smaller ω, and increases somewhat at larger ω around, around the region where the tolerance deviates toward its high-frequency asymptote.

When the output phase jitter becomes triangular, like in the figures below, the actual tolerance gradually flattens out towards the asymptote Tol. ≈ LEO.

Acquisition and tracking examples with evidence of slew rate limitations

A 1st order type 1 loop goes into slew rate limiting (= into slewing) only because of the VCO range limits

The slew-rate occurs when the VCO frequency can not track the input jitter frequency.

In a 1st order type 1 loop this only occurs when the VCO reaches one or both the extremes of its frequency range.

(If f_p ≠ f_fr the maximum frequency swing that is possible in one direction is shorter than in the other direction, which means that the slew-rate in the corresponding direction is less steep than the slew-rate in the other, or that it is not present at all.)

Time diagram of phase waveforms at input and output of a 1 - 1 CDR during acquisition and tracking.
The CDR is slew rate limited, and the asymmetry of the slew-rates originates from the inaccuracy of the VCO free-running frequency.
The initial acquisition phases are deliberately made short and simple to focus on the tracking phase.

During the first 100 simulation steps (1.78 nsec) there is no input signal.

LOS is asserted in this interval and the CDR is free-running at its centre frequency ω_ffr, that is 2000 ppm ( 0.2% ) slower than the nominal link frequency ( i.e. the frequency of the remote transmitter) of 6.28 10¹⁰ rad/sec. After 1.78 nsec the PLL lags 0.22 rad behind the transmit clock.

Then the input signal appears (LOS is dis-asserted) with a "step" of +1.25 rad (useful to mark the beginning of the acquisition phase).

The input signal is flat in phase for the time being (no jitter yet).

The phase detector jumps from its intermediate state (that was forced by the LOS signal) to its upper state, signalling that a delay is detected.

This jump propagates without appreciable delay to the VCO drive signal: the VCO jumps to its maximum possible frequency (D_T of the incoming signal is 50%) and its phase (i.e. the CDR output phase) increases linearly with its maximum possible slope.

The VCO maximum frequency is 7.743 10⁸ rad/sec (=12324 ppm) higher than ω_p (6.28e10 rad/sec), but this value must be reduced because the actual D_T is < 100% (D_T=50%), in order to obtain the maximum possible value of 4.71 10⁸ rad/sec (=7499 ppm), that is the "rising" slew-rate of this CDR in the present conditions.

In a similar way, the "falling" slew-rate of this CDR is -7.22 10⁸ rad/sec (=-11499 ppm). It is larger because of the offset between ω_fr and ω_p (2000 ppm, i.e. by 1.257e8 rad/sec).

The output phase catches up with the input after 4.9 nsec.

The bang-bang detector, that has been frozen to its upper level during the catch-up transient, starts now its typical pattern of bang-bang frequent jumps.

It may also be remarked that, as long as the PD follows its typical bang-bang pattern, the distance in phase between input and output (=the error signal) remains very close to zero, and there is no evidence of the steady-state phase error typical of linear systems. In this condition the PD operates very close to its middle point, where its gain is extremely high: the steady stye error of a type 1 system can be computed as the angular frequency offset, divided by the open loop gain. As the gain is almost infinite, the error is almost zero during this interval.

When 300 simulation steps have elapsed (5.35 nsec), the input signal starts an additional sinusoidal jitter with an angular frequency of 7.5 10⁸ rad/sec and a peak amplitude of 1.20 rad.

The sinusoidal component of the input jitter starts with its maximum slope (9.0 10⁸ rad/sec) and the slew-rate that the PLL can produce is slightly smaller: as indicated above it is 4.71 10⁸ rad/sec

The output phase cannot follow the input but follows its maximum slope until the input slows down and it can track it again. This happens 2.46 nsec after the start of the sinusoidal jitter.

Then the tracking resumes until the falling slope of the input sinusoidal jitter becomes too steep and exceeds the maximum negative slew-rate that is -7.22 10⁸ rad/sec.

Once there has been tracking at one peak of the input sinusoid, all the subsequent cycles are identical, and the average value of the phase error waveform generates the average drive error at the VCO input that corrects the ω_p - ω_ffr difference.

A 2nd order type 2 loop goes into slew rate limiting because of the limited HF gain of the loop filter

When tracking becomes difficult because the loop must operate close to its ability to track, the effort becomes evident by the periodic deviation of the phase comparator output (same period as the input jitter) from its average level. In case of a phase detector, such effort is made evident by a reduction of the bang-bang duty-cycle. Around the zero-crossing of the input jitter sinusoid, the PD output stays constant and indicates the onset of a phase error due to slewing.

The sinusoidal jitter signal must be considered in conjunction with the steady state error because a type 1 loop compensates all frequency differences and wander with a shift of the bias level of the signal driving the VCO. The slew rate slope of the CDR response is consequently increased in one direction and reduced by the same amount in the other direction. This would be exactly true if the VCO corresponded to its simulation model, but is just approximately true because the actual VCO characteristic is never so neat, symmetric and and simple.

Slewing can be defined as a contiguous sequence of ten or more identical phase-error indications.

When the jitter frequency is too high for a correct tracking, the slew-rate covers the entire jitter period, and the output jitter becomes a triangular saw-tooth of reduced amplitude.The CDR still tracks well because the steady-state frequency error ω_p - ω_fr is tracked as well, as can be seen in the asymmetry of the triangular output wave.

The following figure illustrates the above remarks with the phase signals of a typical CDR (in this example, a 2-2 loop with PFD).

Slew-rate limitations at medium and at high jitter frequencies.
The triangular wave of the output at high frequencies is symmetric: the type 2 loop squeezes to zero any steady state output error.

In this figure the slew rate occurs (at both low and high jitter frequencies) because of the very low gain of the loop filter at frequencies higher than ω_z (the frequency of the zero of the loop filter).

The waveform (in black) of the VCO drive signal bang-bangs when there is no slewing, and slowly ramps away as long as the phase error keeps the same sign (constant slew-rate condition of either sign). The steep bang transitions and the slope of the ramps that follow implement the step response of the loop filter driven by the steps (bang-bangs) of the PD output. In the PD output, the slow ramp during slewing compensates any possible steady-state error of the loop output.

There is also -in a 2nd order type 2 loop- the other source of slew-rate generated by a frequency clamp (the overall limitation of the VCO frequency range) forced either by the saturation of the output of the loop filter at large signals, or by the saturation of the VCO characteristic at the extremes of its frequency range.

This second source of slew-rate obviously takes places with much larger Δω and much smaller ω. In type 1 loops it is the only source of slew-rate (as seen in the previous example).

Onset of slewing in a 2nd order type 2 CDR with bang-bang PD and its curve of VCO range limits

This example is interesting because it corresponds to an architecture that is quite common, and also because it points out an intriguing analogy between the linear model of a 2-2 loop and this application of a non-linear 2-2 architecture.

The frequency of a VCO in a 2-2 CDR with bang-bang PD is limited in its excursion either because of:

1. the limited amplification (variable with the jitter frequency) of the filter block, that receives the square wave of fixed amplitude coming out of the PD and that then drives the VCO frequency, or
2. the rapid fall of the VCO gain at the extremes of the VCO characteristic (to simplify it is assumed here that the VCO characteristic is linear inside the range, and flat outside).

The limitation of the VCO frequency is therefore a curve as in the following figure:

The possible frequency swing of the VCO in a 2nd order type 2 CDR is limited,
and the limits vary with the jitter frequency used to inspect them.

The curve plotted (fine red line) approximates the curve of max frequency swing of the VCO using the condition of onset of slewing.

It should be kept in mind that the linear model (green curve in the figure at the page beginning) plots a tolerance function, while the onset of slewing plots a prudent boundary that is lower than the actual tolerance function.

As long as the loop keeps on tracking, the PD maintains its continuous bang-bang and the phase error in front of the PD remains very limited. For a run-length of n, it is limited by 2 Δφ_b-b + (n-1)Δφ_fp-ffr..

For jitter frequencies of ω_j higher than ω_z, the waveform at the PD output is amplified by G_f and then used to drive the VCO.

For jitter frequencies ω_j lower than ω_z, the fundamental component of the waveform at the PD output is amplified by G_fω_z / ω_j , which is higher than G_f, and the loop is able to track at the onset of slewing following the slope (-20 dB/dec) of the gain G_fω_z / ω_j versus ω_j curve, down to the point where the VCO frequency swing can grow no more and the curve becomes horizontal.

As long as the slew-rate of the incoming jitter A_jω_j corresponds to a frequency that is below the curve in the figure above, there will be no slewing and the incoming jitter will be perfectly tolerated.

If the diagram above (tolerable frequency swing as a function of the frequency of the sinusoidal input jitter) is translated into the classic tolerance format (tolerable phase amplitude as a function of the frequency of the sinusoidal input jitter),

then the slopes of 0 and of -20 dB/dec become respectively -20 and - 40 dB/dec.
The addition of the horizontal asymptote corresponding to the tolerance always present because of the LEO buffer,
the tolerance function is approximated by the mask in the following figure:

The phase tolerance in a 2nd order type 2 CDR can be (prudently) approximated, in its frequency dependent part, using the condition of slew-rate onset. The phase tolerance there can be derived from the frequency range possible for its VCO.

In the segment at -40 dB/dec, there are two 90° phase rotations at play:

• the negative slope of the loop filter
• the integration frequency-to-phase in the VCO.

This consideration (fully valid in a linear domain) still holds good here: it can be found that the CDR slewing does not appear starting from the instants of maximum slope of the input jitter (what it does normally in correspondence to a -20 dB/dec slope of the tolerance curve),

but at the instants of peak of the input jitter.

It may be said that this corresponds to a 90° rotation of the CDR output phase...

The following figure shows tolerance curves (in dB and in UI) obtained by numerical simulations.

Tolerance curves in dB and in UI obtained by simulation of a 2 -2 CDR with PFD and transition stuffing.
The LEO is set at a low value of 1 rad. The asymptotes are positioned manually over the interpolated dB curve.
A good agreement is found between the corner point of the two oblique asymptotes and the ω_z given value of 4.0 10⁺⁵.

It may be noted that the asymptotic tolerance at high frequencies is slightly lower that the minimum usually specified of 0.15 UI.

This is a consequence of having used the pessimistic value of 1 rad for the Lateral Eye Opening.

The limited range of the (possible) elastic buffer

In general, a buffer may come in various forms, grouped here below in three categories of decreasing added delay:

• Buffer memories used to store and forward large amounts of bits, like packets of a TCP/IP protocol.

  They are often organised by byte, and are written and read with clocks running at the byte rate.

  The memory is so deep -and the added delay is so large with respect to the bit period- that they easily absorb the timing jitter or the frequency mismatch between the write and the read clocks.

  These buffers could be located inside a single clock domain or at the border of two different domains.

• Elastic buffers between clock domains.

  They are meant to absorb or at least to mitigate the effects of jitter, wander and drifts between the clocks of the two domains.

  Their depth is chosen to absorb the clocks drifts with as rare slips as possible. These elastic buffers are not as deep as a buffer memory but much deeper than a phase adder in a phase aligner (see below).

  As there is no prior knowledge of the drift sign, their end of range triggers a reset to the central point.

  They deal with serial transmissions and are essentially based on shift registers clocked with the incoming clock and read with the local clock.

  Their tolerance is studied using linear phase ramps.

• Phase adders for Phase aligner CDRs.

  Only a clock domain is involved and there are no d.c. drifts between the incoming signal and the local clock.

  They are meant to absorb just the a.c. jitter that has been generated in a relatively short timing loop inside an equipment or in a downstream/upstream loop of an access network.

  Their tolerance is studied with sinusoidal jitter i.e. with Fourier transforms.

  The border of linear operation (= of the tolerance) of a phase adder is typically found when the algebraic sum of the phases of its two inputs reaches the minimum or the maximum value allowed for the output range of the adder.

  It does not depend on the value of either input, even though in practice such limits of tolerance are often reached when one input simply swings too wide.

  The mathematical model shall be:

Magnitude of [I₁(jω) + I₂(jω)] = |I₁(jω) + I₂(jω)| = Φ_max

where +/- Φ_max are the largest values that the adder can process linearly.

As there is no drift at all, but just alternating jitter, at the end-of-range the adder saturates (as explained below for the delay line implementation).

The model (of steady state condition), with |I₁(jω) + I₂(jω)| = 0 for the mid output point, is chosen because it matches the corresponding hypothesis that, if the initial delay was not the mid point, then a transient out-of-range with subsequent re-centering has occurred.

The phase adder of a PLL is a delay line

In PLLs the phase adder is implemented in the form of a delay line. The input of the delay line is one input of the adder, while the other input simply controls the amount of delay added to the signal that enters the delay line.

Such adders can tolerate an added delay between zero and the maximum length of the delay line, D_max.

The delay can also be measured as a phase, in units of radians at the angular frequency of interest.
If a delay is known in seconds, then it can be be converted into radian
multiplying it by the angular clock frequency: [sec] * [rad * sec⁻¹] = [rad].

The tolerance limit will be in such cases modeled as:

0 < added delay < D_max.

When the tolerance extremes are exceeded, the delay lines simply saturates in the sense that it either does not add any delay or that it keeps on adding its maximum delay D_max. In terms of signal phases, the output remains constant at its minimum or maximum value.

In the case of a phase phase lock loop incorporating the delay line, this means opening the loop until the input jitter changes its direction of variation. The delay range is frozen while the input jitter waveform insists in the same direction and until it starts getting back. At that moment the lock resumes, but the delay range is now translated towards the average value of the incoming jitter by the amount of the sidetracking.

This achieves some sort of translation of the delay range towards re-centering around the average value of the input the jitter. It is important to observe that this takes place in a discontinuous mode, because the loop keeps on re-locking into the center of the closest pulse in the delayed waveform presented to its phase comparator. This adds an imprecision of ± π to the positioning of the delay line with respect to the incoming signal, and consequently to the loop jitter tolerance from that moment onwards.

The granularity of the delay line can be as coarse as about 1/3 of the line pulse period (π/2 - ε in theory), or as fine as fraction of one percent of such period. This granularity adds to the imprecision of the point above to reduce the resulting tolerance.

To model the phase tolerance curve associated to the delay line in the phase alignerthe following points are considered:

- Initial conditions. Sufficient re-centerings have occurred in the past, and presently the delay is centered with the inevitable imprecision of ± π

- A granularity of Φ_gran characterizes the delay line;

- total delay that the delay line can adjust is D_max:

The tolerance limit imposed by the phase adder to the phase aligner is a fixed amount at all frequencies and is modeled as follows:

|X(jω)| < (D_max/2 - π - Φ_gran)

The curves in the figure above can be seen as examples of tolerance of phase adders in the flat part at low frequencies.. Such clamping of the curves at low frequencies if present because the tolerance of the elastic buffer (present in the circuits of the figure) is independent from the jitter frequency and only depends on the length of the buffer. The tolerance due to the lateral eye closure further reduces the tolerance at mid and high frequencies and ultimately flattens out at very high frequencies, as seen just above.

Jitter tolerance and VCO modulation

When the CDR operates along the tolerance border, its periodic output is made by two periodic signal parts:

1. the tracking
2. the error.

When tracking is the larger part, the angle ( function of $\omega _{m}$ ) represented by the FM modulation index $h$ of the VCO overlaps (almost) with the tolerance function.

When tracking is the smaller part and the error is the larger, the tolerance angle tends to the buffer depth and the modulation index becomes very small.

Both jitter tolerance and FM modulation index $h$ are defined in the sinusoidal regime.

Focusing on the PLL VCO as a FM modulator:

modulation index $h={\tfrac {\Delta {}f}{f_{m}}}={\tfrac {\Delta {}f_{VCO}}{f_{m}}}={\tfrac {\Delta {}\omega _{VCO}}{\omega _{m}}}$

where $f_{m}\,$ (or $\omega _{m}\,$) is the highest frequency component present in the modulating signal ( i.e. in the VCO drive signal ), and $\Delta {}f\,$ (or $\Delta {}\omega \,$)is the peak frequency-deviation ( i.e. the maximum deviation of the VCO instantaneous frequency from the un-modulated carrier frequency $f_{fr}$ (or $\omega _{fr}$).

The modulation index is also a measure ( in rad) of the peak phase deviation of the VCO output, with respect to the phase of the VCO output if the VCO was running at f_fr or at f_p

A d.c. component in the modulating signal (like f_p - f_fr) does not change the modulation index, but simply shifts the carrier frequency (in the specific example, from f_fr to f_p), which is nothing but d.c. FM.

The jitter tolerance is defined and measured for individual frequencies of input jitter sinusoids. For each frequency the amplitude of the input sinusoid is increased up to the value where errors appear.

These errors are typically generated when the VCO output jitters too wide and samples the signal eye outside the corners defined by the Lateral Eye Tolerance.

It is convenient to define some sections of the jitter tolerance functions by the onset of other non linearities of the CDR (slew-rate), but in actuality such sections lie slightly below it the true border of tolerance.

The two quantities are closely related. The jitter tolerance limit In a CDR coincides in a wide frequency range with $h$, that is the phase deviation of the VCO in that CDR.

Definition : $\omega _{mc}$ is the frequency at which the corner with the high frequency asymptote takes place in the tolerance curve.

This definition of $\omega _{mc}$ applies both to linear type 1 slave CDRs and to bang-bang CDRs of type 1 and 2, as:

1. there is no more tracking at higher frequencies in both cases, and
2. the two cases cover all the applications of CDRs .

Moreover, $\omega _{mc}$ is the 3 dB point of the tolerance curve both for a the linear architecture and for the two bang-bang architectures used in practical applications.

• If the jitter frequency is exactly $\omega _{mc}$, the tolerance value is about 3 dB higher than the high frequency asymptote, i.e. the tolerance is:

${\sqrt {2}}\left(\Phi _{LEO}-E_{S}\right)$

The sinusoidal jitter amplitude tolerated by the CDR input at $\omega _{mc}$ is the sum of two (about equal but orthogonal) sinusoids. One part represents what is not tracked by the CDR (i.e. is absorbed by the phase comparator buffer)

The other half is tracked because it appears at the output of the VCO. Therefore:

$h=\left(\Phi _{LEO}-E_{S}\right)\approx \Phi _{LEO}$

• At frequencies >> $\omega _{mc}$ the tolerance is exactly the lateral eye opening Φ_LEO (more precisely: Φ_LEO - steady state error).

The modulating signal ( i.e. of the VCO input ) originates at the phase-comparator output.

By definition, the phase comparator output is the phase-error that the loop is unable to track.

In sinusoidal regime, the CDR loop is unable to track the frequencies much higher than $\omega _{mc}$, and those high frequencies do not reach and do not modulate the VCO.

At those high frequencies the CDR input can jitter up to about ± Φ_LEO and still be tolerated, but the VCO output phase does not jitter appreciably.

Nonetheless, if the definition of $h$ is stretched a bit, it can be seen that the VCO modulating signal depends on the input jitter frequency according to 1/f. A point of this function is already known at $\omega _{mc}$. As a result, in this frequency region:

$h\approx \Phi _{LEO}{\frac {\omega _{mc}}{\omega _{m}}}$

• If the jitter frequency decreases down from $\omega _{mc}$, the CDR tracks the input jitter more and more (i.e. the VCO phase deviates more and more ).

The amplitude of the tolerated jitter becomes >> Φ_LEO.

An input signal of increasing amplitude is accepted (= tolerated) the test frequency $\omega _{m}$ decreases, but there is always a periodic error of constant peak amplitude VCO output.

The VCO output can be seen as the sum of a sinusoid identical to the CDR input, plus an error signal. The error signal has the same period of the CDR input sinusoid, may or may not be sinusoidal, is always out of phase with the input of the CDR and has a peak of $\left(\Phi _{LEO}-E_{S}\right)\approx \Phi _{LEO}$.

From $\omega _{mc}$ downwards to lower frequencies, the amplitude of the input sinusoid increases (with ${\tfrac {1}{\omega }}$ or${\tfrac {1}{\omega ^{2}}}$, while the periodic error signal keeps the same peak value and becomes therefore rapidly negligible.

As a result, in this frequency region:

$h\approx {jitter}\ {tolerance}\ function$

In the sinusoidal regime it is possible to contrast directly the FM modulation index of the VCO ( $h$ ) with the tolerance function of the whole CDR.

The two functions ( of $\omega _{m}$ ) vary, depending on the CDR architecture, on the loop gain G, etc. .

In any case, the two functions practically overlap each other for low and medium values of $\omega _{m}$ (up to $\omega _{mc}$ ), and diverge at higher values of $\omega _{m}$, where they follow respectively a -20 dB/dec asymptote and a flat asymptote.

The three figures below show the simplified asymptotic Bode plots for both functions, in the cases of the 3 fundamental architectures used in CDR applications.

Asymptotic diagrams for the simplest case of a 1st order type 1 architecture using a bang-bang phase detector.
The low and mid frequencies part corresponds to the onset of slew-rate when the peak of the VCO drive signal reaches ±V_D

Asymptotic diagrams for the medium complexity case of a 2nd order type 1 architecture using a linear phase comparator.
The low and mid frequencies part corresponds to the CDR operation in linear mode with a phase error amplitude of $\approx \Phi _{LEO}$

Asymptotic diagrams for the most complex case of a 2nd order type 2 architecture using a bang-bang phase detector.The three asymptotic regions to the left correspond to:
- leftmost: slew-rate onset with VCO drive reaching ±V_D
-- middle: linear CDR operation with a peak input phase error of $\approx \Phi _{LEO}-\Phi _{bb}$
--- rightmost: slew-rate onset with VCO drive at either +/- V_bb for more than 10 consecutive U.I.

Narrowband FM

As long as the modulation index h of the FM remains below 1 (say no more than 0.3 ), the FM is called narrow-band and its spectrum is very close to the spectrum of an amplitude modulation (AM) that be generated with the same carrier wave and the same modulating signal.

The Φ_LEO is, with a first approximation valid for most applications of CDRs, ≥ 1 rad (i.e. ≥ 0.15 UI ).

In normal tracking conditions the CDR operates with at least 10 dB margin, that brings the jitter peak down to about 0.3 rad.

With h < 0.3 rad, FM is a narrowband FM.

In the CDR, the baseband jitter spectrum present at the VCO input becomes, at the VCO output, very similar to an AM spectrum modulated around f_fr, and keeps its "shape" without the distortion typical of wideband FM.

During acquisition transients and in case of extremely noisy applicative conditions, the VCO modulation may occasionally deviate from this "quiet" condition.

Considerations

• It should be emphasized that the jitter tolerance function is:
  • neither a transfer function (its output is not generated with input sinusoids of unit amplitude)
  • nor a part of the mathematical model in the strict sense
    (because it depends on non-linearities for its definition, although it is computed within the boundary of the circuit linear operation, and
    because it may be different for different architectural variants belonging to the same model architecture. See the example of the 1st order type 1 phase aligner that has a different tolerance from the 1st order type 1 slave).
• In the cases where the tolerance function is determined only by the maximum difference acceptable inside the phase comparator, the tolerance limit is a consequence of the one sided eye opening and not of the comparator range (that is larger).

Exceeding the comparator range (±π) generates slips (= very high BER), but exceeding only the lateral eye opening just generates error bursts that can be rather short. The lateral eye opening is reached always before the comparator range is exceeded: the tolerance function (as well as the tolerance curve!) corresponds to the errors that occur at the eye corners. Phase comparator slips (and associated errors) do occur in a CDR, but beyond the limit of tolerance set by the lateral eye aperture.

The high frequency jitter tolerance corresponds to the LEO and is visible (and measurable) as the horizontal asymptote at the highest frequencies of jitter. From a certain frequency up:

the PLL does not track at all,

the jitter imposed to the input signal moves back and forward the signal transitions (already affected by I.I., noise etc.) and

the sampling clock does not move.

The tolerance function, derived from equating the phase error to the eye opening, in such case replicates very well, in magnitude, characteristic asymptotes and corner frequencies the diagram that is obtained with actual measurements.

• Where different phenomena cause each a different region of tolerance for a CDR, then the overall CDR tolerance will correspond to a combination of those tolerance regions.